1. Introduction
The non-cognitive constructs of feeling and intuition in the lives of human kind have long been a source of fascination and intrigue. Their illusive and spontaneous qualities have meant that their investigation has been difficult particularly as these pertain to learning, teaching, problem solving and decision making. Tradition has held that information obtained through non-cognitive means is unreliable and further that sound thinking requires “getting feeling out of the way” (Immordino-Yang & Faeth, 2010: 76).
Understanding of the cognitive nature of human thinking (as with models of learning and teaching), arose during the industrial age of the eighteenth and nineteenth centuries, where analogies were drawn with power driven machinery. Questions such as “what is the power?” and “what is the machine?” were typical of this period. Utilising notions of the instinctive drive, feeling and emotion were conceptualised as the “power”; and intelligence or reason as the “machine” (Wallas, 1926). Consequently it was necessary for the emotionally actuated human to be instrumented by reason (Aldous, 2013; Wallas, 1926).
Given the association of emotion with “power” and reason with “machine” it was perhaps not surprising then, to have found scientists in the latter half of the twentieth century pursuing cognition’s more respectable aspects (Broadbent, 1958). Indeed models of human information processing drew analogy with the computing machine where speed of processing and size of working memory were keys (Anderson, 1995). However, the involvement of non-cognitive components such as feeling, intuition and emotion were in the main nowhere to be seen. While the contribution that cognitive models have made to understanding about reasoning and problem solving is considerable there is still much to be done in comprehending the role of non-cognitive components in thinking and reasoning and further of considering how both cognitive and non-cognitive processes interact to produce successful solutions, profitable decisions and wise counselling.
One neuroscientist and medical practitioner to be confronted with the omission of non-cognitive elements in models of human reasoning and decision making was Damasio (1994). Working with brain damaged patients having lesions in a small region of the prefrontal cortex, Damasio found individuals presenting with normal IQ, language ability and learning capacity being unable to solve problems. In problem solving situations these individuals were unable to decide between two rational alternatives. The patients were perfectly rational on all psychological tests and yet because the connection between the feeling function and reasoning in the brain had been impaired could not bring reasoning to any practical conclusion. Damasio concluded, contrary to traditional viewpoints that feelings are just as cognitive as other precepts and that feeling is required to move through a decision making space (Damasio, 1994, 1999).
Damasio (1994) went on to describe three classes of feeling. These classes are feelings of basic universal emotions, feelings of subtle universal emotions and background feelings. Feelings, arising from the complex interplay of the brain core (viz: hind brain, mid brain and limbic systems) and the cerebral cortex serve to provide a window on the body’s internal state which can then be weighed with information received from the external one. Such feelings Damasio (1999) advises are essential to human survival and consciousness.
One notable scientist, early last century who reported attending to feeling in the solving of novel problems within the field of mathematics was Poincare (Poincare, 1924). While Poincare believed his memory to be insufficient for remembering the very large number of moves required of a world class chess player, he pondered why it was the case that he could invent new mathematics and yet a world class chess player could not or did not. He attributed his creative capacity to his ability to attend to a feeling of cognition. The feeling to which he referred was not an emotional one in the universal sense as described by Damasio, but rather more of a background feeling in the aesthetic sense, that guided him to a new intellectual order still eluding rational grasp (Ghiselin, 1963).
Another example of an important role for feeling and intuition, this time in relation to learning is to be found in research using the Iowa Gambling Task (IGT) (Bechara, Damasio, Tranel, & Damasio, 2005). In the IGT individuals are presented with four decks of cards where the purpose of the game is to win as much money as possible. Two decks yield high gains but high losses while two decks yield small gains and small losses. Should individuals continuously choose cards from the high gain high loss decks then a net loss results. However should cards be chosen continuously from the small gains but small loss desks then a net gain will result. Importantly, the participants involved in the IGT are unaware of the rules of engagement and needed to learn these for themselves by deducing, the relative long term outcomes of different decks. Of note to the discussion in this paper was the finding that through measures of galvanic skin response or GSR in which microscopic amounts of sweat on the palms were measured, an anticipatory emotional response in the moment before choosing a card from a high risk deck was observed (Bechara & Damasio, 1997). Thus a risk assessment of each deck was intuited through non-cognitive processing prior to conscious awareness. This non-cognitive emotional information was needed to guide participants to the so called safe decks. It was concluded that the development of non-conscious emotional information therefore was important to learning which in this example involved learning the rules of engagement. The knowledge constructed through non-cognitive means was important for problem solving and for enabling a rational decision to be made (Werner, Duschek, & Schandry, 2009). Hence in learning how to play the IGT game both non-cognitive and cognitive information needed to be attended to.
Interestingly, in a large scale study of the IGT in which participants ranged in age from 10 to 30 years, the tendency to play from the high risk decks was found to peak in mid to late adolescence (i.e. ages 15 - 19). Similarly the tendency to refrain from playing high risk decks increased linearly with age, with adults avoiding disadvantageous decks at rates higher than both preadolescent and adolescent groups (Cauffman et al., 2010). Results from studies such as these would seem to indicate that both preadolescent and adolescent people would likely benefit from counseling that encouraged attention to feeling and other non-cognitive information such as that of skilled intuition particularly when solving complex problems or making high stake decisions.
Hence evidence is accumulating to indicate an important role for both cognitive and non-cognitive processing in problem solving, decision making and learning. It is also pointing to an important role in the process of creativity (Aldous, 2012). However, the situation remains unclear as to whether and how well adolescent students attend to non-cognitive information when solving novel problems particularly in the context of learning and teaching. Further, what relationship exists between attending to feeling and skilled intuition and success in a creative problem solving event?
The following study outlines an investigation into the cognitive and non-cognitive approaches to reasoning used by adolescent students when solving novel problems in the field of mathematics. The learning context involves a national event referred to as the Mathematics Challenge for Young Australians, in which students in primary and secondary schools across the nation are invited to participate. In this activity each student has three weeks in which to answer six novel problems. Some schools choose to embed the Australian Mathematics Challenge into their curricula and teaching so that every student in the school participates. Others run the activity as a self selecting event so that only those students who want to be involved do so.
The investigation requires the identification of two systems of reasoning broadly defined as cognitive and non-cognitive. The measures of reasoning employed in this study are those grounded in Sloman’s (1996) and Epsteins’s (1994, 1998) two systems of reasoning and patterns of mind. In particular, measures of cognitive processing are aligned with the rule based systems of reasoning (Sloman, 1996) and the analytical-rational patterns of mind (Epstein, 1994, 1998). The non-cognitive measures are aligned with the associative system of reasoning (Sloman, 1996) and the intuitive-experiential patterns of mind (Epstein, 1994, 1998). Further, these measures are consistent with System 1 and System 2 thinking, elaborated on by noble laureate Daniel Kahneman (Kahneman, 2011).
The following questions were used to guide the conduct of research. These are:
1) What cognitive and non-cognitive approaches to reasoning do middle school students use when solving novel problems in mathematics?
2) What relationships exist among cognitive and non-cognitive approaches to reasoning and how do they interact?
3) What relationships exist among cognitive and non-cognitive approaches to reasoning and success in novel mathematics problem solving?
2. Method
2.1. Participants
The data comprised a non-random sample of participants enrolled in the Mathematics Challenge for Young Australians (2001) and in schools that had agreed to their students undertaking further tests and answering additional questions aligned with the investigation. They were 405 middle school students in Grades 7 to 10 from among 11 independent schools across two states of Australia. Of these, 199 were female and 206 were male. The participants ranged in age from 11 to 16 years (mean age = 13.9 years, SD = 1.0).
2.2. Path Modelling with Latent Variables
Latent Variables
The words “latent variables” mean hidden or concealed variables that cannot be measured or observed directly (Vogt, 1999). Since this study was to investigate hidden mental and emotional processes in a novel mathematics problem solving event the construction of variables that could measure latent constructs was important. This was ever more the case when considering intangible concepts such as feeling and intuition.
Structural equation modelling (SEM) with latent variables permits abstract variables not readily observed to be represented in statistical analyses (Sellin & Keeves, 1997). This is done by allowing multiple indicators, considered to be manifestations of the latent construct, to form or reflect the latent variable. The indicators used to construct the latent variable are termed manifest variates (Evans, Hastings, & Peacock, 2000). Latent variables formed from multiple variates have been found to have greater reliability and validity than variables singly observed (Sellin & Keeves, 1997).
This study was designed to have 20 latent variables with 20 cases for each latent variable. No latent variable had more than 10 manifest variates. These 20 latent variables were used to build a meaningful model of creative problem solving The context of creative problem solving was employed since within the realm of cognition, investigations of creativity permit non-cognitive as well as cognitive elements to be examined. In particular intuition has been found to be a critical component of creative thought (Eubanks, Murphy, & Mumford, 2010).
Creativity is of itself a highly complex construct; however, space does not permit a full elaboration here. Nevertheless, four dimensions of creativity were involved in building the model. These were the Person, the Process, the Product and the Environment dimensions. The Person dimension focuses on the extrinsic skills and abilities that mark the creative person, the Process dimension on the patterns of reasoning used by the creative mind, the Product dimension on the pattern of criteria that distinguishes a creative product, while the Environment dimension focuses on the patterns of circumstance that surround the creative individual (Mooney, 1963).
2.3. Theoretical Constructs and Dimensions of Creativity
In the context of learning and teaching seven theoretical constructs (although not exclusively so) were considered important in the construction of a path model of creative problem solving. These constructs related to factors of school learning identified in Carroll’s (1963) “Model of School Learning” as well as to the employment of different creative processes used in creative problem solving that have been identified in Shaw’s (1989) “Model of the Eureka Process” and Amabile’s (1983, 1996) “Social Psychology of the Creative Process”. The constructs pertained first of all to a set of Antecedents, as well as to a student’s Personal abilities, Perseverance and motivation, Opportunity to learn, Quality of instruction, Achievement outcome and Approaches to reasoning. In the former case, Antecedents are considered to come early in a causal chain of explanation, preceding any other conditions under investigation (Vogt, 1999). In this study the antecedents comprised a student’s sex, age, year level and type of school attended, be it single sex or co-educational. In the later example the Approaches to reasoning construct arose much later in the causal chain of explanation and was the locus where the feeling and intuitive approaches to reasoning were investigated.
The Approaches to reasoning construct pertained to the use of cognitive and non-cognitive systems of reasoning when solving a novel problem. Measures of this construct were obtained through a self report instrument known as the Systems of Reasoning Questionnaire (SRQ). The SRQ, was initially developed by Aldous (2001, 2006) and subsequently validated in a cross case analysis by Jefferies (2011). This construct, comprised the Process dimension of creative problem solving. The Personal abilities, Perseverance and motivation constructs comprised the Person dimension while Opportunity to learn and Quality of instruction, synthesized into the Experiences construct comprised the Environment dimension. Finally, the Achievement or outcome construct comprised the Product dimension of creative problem solving.
Theoretical and temporal considerations suggested a central explanatory scheme of Antecedents à Abilities à Experiences à Motivation à Approaches à Outcome. However, it is acknowledged that this is but one of a number of possible causal schemes. Further, any construct arising early in the chain of causality may influence all other constructs sequenced after it, resulting in a complex web of possible direct and indirect relationships. The constructs comprise 20 latent variables. The latent variables, their associated manifest variates grouped by dimension and construct are given in Table 1.
2.4. Modelling with PLSPATH
One program using Partial Least Squares (PLS) procedures that readily provides for the construction of latent variables and the examination of path models is the computer program PLSPATH (Sellin, 1990). Causal modelling with PLSPATH permits complex sets of relationships between many variables, both latent and manifest to be explored (Noonan & Wold, 1988; Rigdon, 2012). Such relationships are tested in the context of a desired outcome or criterion, which in this study was success in novel mathematics problem solving. Of benefit to the current study was the fact that PLSPATH does not demand normally distributed data and in particular employs formative, unity and reflective modes in the construction of latent variables (Rigdon, 2012). Since, PLSPATH does not use co-variance structure analyses it can be employed with small samples (e.g. n = 50) (Haenlein & Kaplan, 2004). In addition it does not depend on the use of formulae to calculate standard errors but employs bootstrapping and jack-knifing procedures. Although first developed in the early 1970s, modelling with PLSPATH is receiving heightened interest particularly in the fields of management and market research (Ringle, Sarstedt, Schlittgen, & Taylor, 2013).
2.5. Specifying the Model
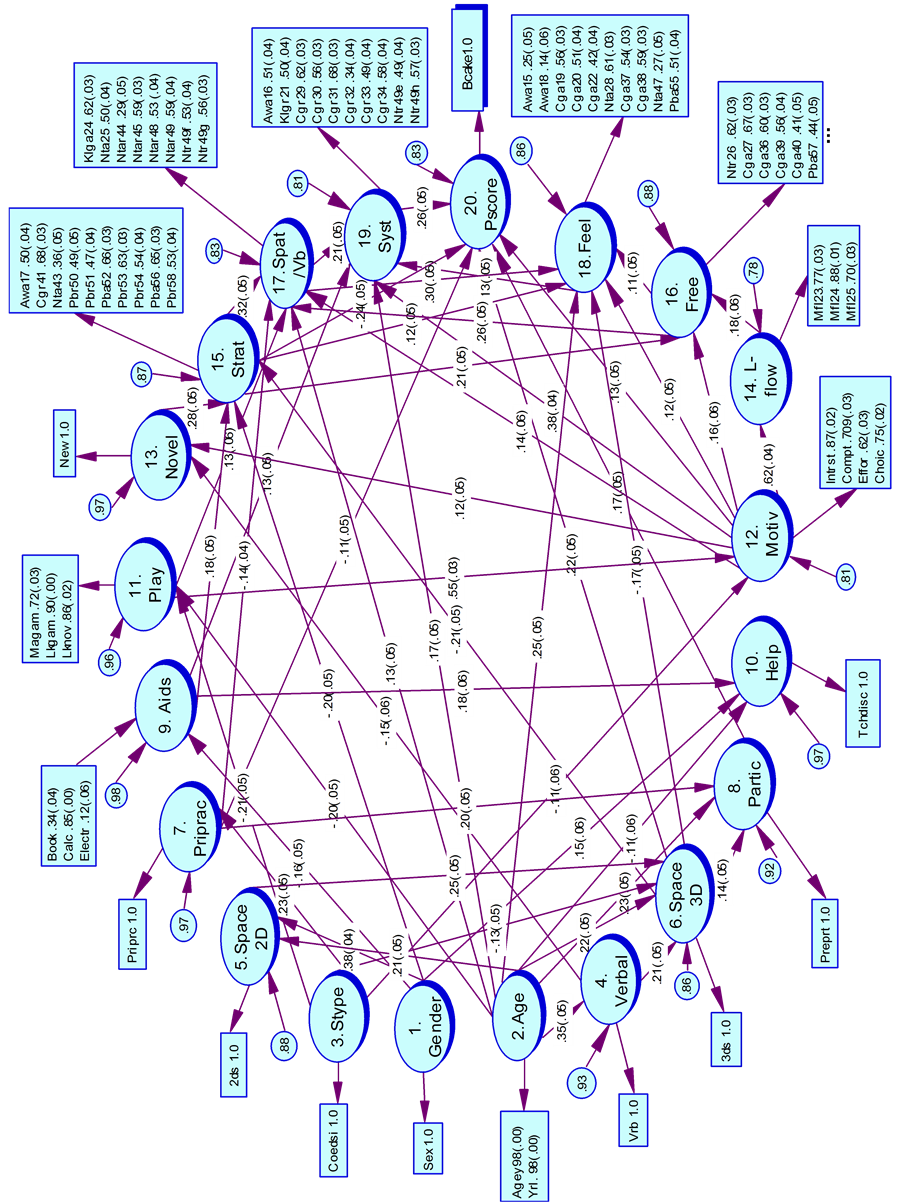
Diagrams showing the specified sequence of latent variables in the causal model of creative problem solving are given in Figure 1 and Figure 2. The specified model, grounded in the explanatory scheme outlined previously, was examined with data collected from two different Mathematics Challenge problems. However, only the final paths in the specified model are indicated. It is important to note that all inner model paths between each latent variable to every other latent variable in the model with the exception of paths between the three antecedent exogenous variables of Gender, Age and School type Stype, where there are none, were examined using PLSPATH Version 3.01 (Sellin, 1990). A description of how non significant paths in both the inner and outer model were removed follows.

Table 1. Latent variables mapped by dimension and manifest variates.

Continued
2.6. Outer Model Paths
The influence of any given variable whether it be manifest or latent is estimated by the size and direction of its standardised regression path coefficient, which signifies the magnitude of effect. In the outer model, the criterion for minimum inclusion of a manifest variate represented in the reflective or outward mode is a loading of ±0.30 (Sellin & Keeves, 1997). In the case of formative or inward mode, the criterion for minimum inclusion in the model is a weight of ±0.10 (Sellin & Keeves, 1997) while in the instance of unity mode the path coefficient is unity (1) The latent variable Aids, described in Table 1 is the only variable constructed using the formative (i.e. inward) mode in the model.
2.7. Inner Model Paths
In specifying the final model for a given data set, paths in the inner model whose path coefficients were less than

1.67 times the jack-knife standard errors were eliminated from the model. However, in general a value of twice the standard error was used. The generation of jack-knife standard errors in PLSPATH is an adaptation of the Stone-Geisser Test (Stone, 1974). In this test, cases are omitted one at a time and model parameters re-estimated on the basis of the remaining cases.
2.8. Measuring Instruments
2.8.1. The Mathematics Challenge for Young Australians
The Mathematics Challenge for Young Australians is organized by the Australian Mathematics Olympiad Committee with the purpose of encouraging as many young people as possible to engage with challenging mathematics problems (Australian Mathematics Trust, 2001). Problems are purposefully designed by a committee to be both novel and challenging. Two problems out of the six alternatives in the Mathematics Challenge were selected for this study. These are summarized below.
2.8.2. The Birthday Cake Problem: Product Dimension
The “Birthday Cake” problem was largely a number based problem that required systematic application of the formula for the area of a triangle and the use of fractional arithmetic. However, some visualisation activity was needed in estimating where and in what manner the Birthday Cake should be cut to meet the limitations expressed by the problem.
2.8.3. The Cute Numbers Problem: Product Dimension
The “Cute Numbers” problem involves a search for pattern in number and the ability to generalize. In particular, successful solution of the problem required finding a pattern that generalized well. The ability to find a pattern that generalizes well is consistent with facility in approximate arithmetic a capacity known to utilize the visual spatial circuits of the brain (Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999).
It should be pointed out that not every participant answered each problem. Some participants answered the Birthday Cake problem only, some answered the Cute Numbers problem only, while still others answered both the Cute Numbers and Birthday Cake problems. From a total of 405 participants, 89% answered the Birthday Cake problem and 96% answered the Cute Numbers problem. The latent variable Pscore is indicated or reflected by (with the arrows in the outward mode) the score obtained on either the Cute Numbers (Cutenos) or Birthday Cake (Bcake) problem. A copy of the problems can be found in Aldous, 2009.
2.9. Systems of Reasoning Questionnaire (SRQ)
2.9.1. Approaches to Reasoning Items: Process Dimension
The cognitive and non-cognitive approaches to reasoning were measured through five scales embedded within the SRQ (Aldous, 2009; Jeffries, 2011). These scales are grounded in Sloman’s (1996) and Epstein’s (1994, 1998) two systems of reasoning and patterns of mind and were used to form the latent variables within the process dimension of creativity. The scales and associated latent variables are the:
• Strategic approach to reasoning (Strat)
• Free-flowing approach to reasoning (Free)
• Spatial-verbal approach to reasoning (Spat/Vb)
• Feeling approach to reasoning (Feel); and the
• Systematic approach to reasoning (Syst)
The scales measuring the Strategic and the Systematic approaches to reasoning are predominantly cognitive in nature, the scales measuring the Free-flowing and Feeling approaches to reasoning are predominantly non-cognitive in nature. The Spatial-verbal scale measures both cognitive and non-cognitive activity depending on whether processing is simultaneous or successive and on whether verbal or non-verbal reasoning or both are involved (Das, 2003).
Example items indicating a cognitive approach to reasoning are, I carefully read the problem more than once (Strategic approach); I used a sequence of logical steps in this problem (Systematic approach). Example items indicating a non-cognitive approach to reasoning are, I used my intuition (followed a gut feeling) solving this problem (Feeling approach); I thought of how to get the answer to this problem while I was doing something else (Free-flowing approach). An example item of the Spatial-verbal approach to reasoning is, often alternated between pictures and words. Respondents answered True (scored two points), False (scored zero points) or Not sure (scored one point) to these statements.
2.9.2. Systematic Approach to Reasoning (Syst)
Ten variates reflected the latent variable Syst. Items (Cgr30, Klgr21) concerned the retrieval of information stored in memory, item (Cgr33) to the utilization of information, item (Cgr34) to the evaluation of information, items (Ntr49e, Nt49h) to the familiarization of information, items (Cgr31, Awr16) to logical, sequential thinking while items (Cgr32, Cgr29) referred to organizational and strategy thinking.
2.9.3. Strategic Approach to Reasoning (Strat)
Ten indicators were used in the formation of the latent variable Strat. These involved the problem solving behaviours of preparation (Pbr51, Pbr50), strategic exploration (Cgr41, Pbr53, Nta43), incubation (Pba52, Pba56), insight and illumination (Pbr58, Awa17) and reflection (Pbr54).
2.9.4. Spatial-Verbal Approach to Reasoning (Spat/Vb)
Eight manifest variates reflected the latent variable Spat/Vb. Item (Ntar49) involved alternating visual and verbal thinking, item (Ntar48) to simultaneous visual and verbal thinking, items (Ntar44, Ntar45) to sequential visual and verbal thinking, item (Ntr49f) to singular verbal thinking and item (Nta25) to singular spatial thinking. Items (Ntr49g, Klga24) involved cue recognition related to verbal and spatial thinking.
2.9.5. Free-Flowing Approach to Reasoning (Free)
Six items tapping semi-conscious and non-conscious behaviours reflected the latent variable Free. These behaviours included defocused attention (Cga39, Cga40), associative thinking (Cga27), cue utilization (Ntr26), breadth of attention (Cga36) and associative illumination (Pba57).
2.9.6. Feeling Approach to Reasoning (Feel)
The latent variable Feel was reflected by 10 manifest variates tapping background feelings, including aesthetic feelings related to the quality and correctness of a solution as well as feelings used in following a hunch about what to do. Items (Pba55, Cga20, Awa18) pertained to intuition, item (Cga19) to imagination, item (Cga37) to originality and inventiveness, items (Cga38, Awar15) to intra-personal checking, item (Cga22) to intuitive insight and items (Nta28, Nta47) to cue activation and cue relevance.
2.10. Antecedent Items
Antecedent information pertained to the student’s sex, age, grade level and type of school attended be it single sex or co-educational. Consistent with PLSPATH modelling procedures, the latent variable Gender, was formed in unity mode by the manifest variate (sex), where girls were coded “0” and boys “1”. The latent variable School type (Stype) was also formed in unity mode by the manifest variate (Coedsi). Participants attending single sex schools were coded “0” and those attending co-educational schools “1”. The latent variable Age was reflected by two manifest variates namely age in years (Agey) and year level of the student (Yrl). This was done since students of appropriate age are distributed across the respective year levels.
2.11. Opportunity to Learn: Environment Dimension
Opportunity to learn items involved an indication of participants’ previous participation in the Mathematics Challenge activity and in prior practice with Mathematics Challenge type problems. Participants indicated the number of times that they had previously participated in the Australian Mathematics Challenge and whether or not they had undertaken practice with past Challenge questions. Previous participation was indicated by the manifest variate (Preprt) reflecting in unity mode the latent variable Participation (Partic). Prior practice with past Challenge problems was indicated by the manifest variate (Priprc) and reflected in unity mode the latent variable Prior practice (Priprac).
2.12. Quality of Instruction: Environment Dimension
Respondents, reporting on the kinds of resources employed to solve the novel problems as well as whether any discussion with the teacher had occurred, were used as indicators of the quality of instruction received. In particular, the use of electronic media (Electr), texts and library books (Book) and calculators (Calc) specified the formation (with the arrows in the inward mode) of the latent variable Aids. The variable, discussion with teacher (Tchdisc), reflected (with the arrow in the outward mode) the latent variable Help.
2.13. Perseverance and Motivation: Person Dimension
Social psychological research by Amabile and others has demonstrated that motivation that arises from an individual’s personal involvement and passion is vital for high levels of creativity to occur (Collins & Amabile, 1999). In this study, measures of intrinsic motivation Motiv were obtained through a set of subscales from the Intrinsic Motivation Inventory (IMI). designed by Deci and Ryan (2001). In particular the scales of Interest and Enjoyment (Intrst), Perceived Competence (Compt), Effort and Importance (Effor), Perceived Choice (Choic) and Pressure and Tension (Press) were used. The Pressure and Tension subscale is a negative indicator of intrinsic motivation while the other scales are positive indicators of intrinsic motivation.
Another indicator related to intrinsic motivation is the concept of “flow” experience as developed by Csikszentmihalyi (1991). An individual will experience flow when his or her level of skill matches the degree of challenge in a given situation. Flow is an indicator or optimal experience (Biasutti, 2011). Three indicators reflected the latent variable L-flow. These were forgetting about time when solving the problem (Mfl23), being really absorbed in finding a solution to the problem (Mfl24) and feeling excited in arriving at a solution to the problem (Mfl25).
Play activity is intrinsically motivated and self directed (Dansky, 1999; Russ & Christian, 2011). Consequently students who spend time playing mathematics games and puzzles in their own time are likely to be more motivated to persevere in a novel problem solving context. Reflectors of the latent variable Play were obtained by asking participants to indicate on a five-point scale ranging from very often to never, their frequency of playing mathematics games and puzzles (Magam), their enjoyment in playing mathematics games and puzzles (Lkgam), and their enjoyment in tackling mathematics problems that are to them completely new and different (Lknov).
For problem solving to be considered creative, the problem presented must of necessity be novel to the individual concerned (Ward, 2011). Given that the degree to which a specified problem is new and different is a personal thing and that the degree of novelty may influence the creative problem solving process (Lubart, 2001), the latent construct Novel, was included in the model. The Novel construct was reflected by the manifest variate (New) where a rating of novelty along a five point scale for a given Challenge problem was recorded.
2.14. The Word Knowledge Test
Verbal Ability: Person Dimension
Language creates the problem space within which individuals perceive and understand a particular task (Katz & Hussey, 2011). Since word knowledge is an indicator of verbal ability, a Word Knowledge Test score (Vrb) was used to reflect the latent variable Verbal. The word knowledge test, comprising 40 dichotomous items, was that used extensively by the International Association for the Evaluation of Educational Achievement (IEA) in international studies of reading comprehension (Lietz, 1995).
2.15. The Card Rotation Test
Two-Dimensional Spatial Ability: Person Dimension
Performance in tests of spatial ability is related to the quality of imagery experienced while carrying out the task (Richardson, 1999). The Card Rotation Test (French, Ekstrom, & Price, 1963) provides a measure of spatial reasoning in two dimensions and is a documented marker for the spatial relations (SR) factor (Carroll, 1993). Hence the score (2ds) on the Card Rotations Test involving a timed test of two-dimensional rotation and reflection of 112 dichotomous items, was used to indicate the latent variable Space2D employed in the model.
2.16. The Surface Development Test
Three-Dimensional Spatial Ability: Person Dimension
In the context of creative problem solving imagery is an important spatial element of human thought that has been likened to an engine in the creative process, (Finke, Ward, & Smith, 1992). The Surface Development Test (French et al., 1963) provides a measure of spatial reasoning in three dimensions and is an indicator for the visualization (VZ) factor (Carroll, 1993). In a timed test, students were asked to imagine folding a series of stereonets into their three-dimensional shapes (3ds) the scores of which were used to indicate the latent variable Space3D.
3. Results
3.1. Outer Model
The PLSPATH results, showing both the inner and outer model standardized estimates for each of the Cute Numbers and Birthday Cake cases of creative problem solving are given in Figure 1 and Figure 2 respectively. With the exception of one manifest variate involving the pressure and tension intrinsic motivation scale, namely (Press) which was deleted in both cases, significant relationships consistent with the 5 per cent level of statistical significance were found between each manifest variate and the latent variable they formed or reflected. In both the Cute Numbers and Birthday Cake cases a mean communality of .46 was obtained for the outer model. This is well above the critical level of .3 proposed by Falk and Miller (1992) and is indicative of robust outer models in both cases.
3.2. Inner Model
In considering the overall strength of the inner model the mean of the multiple R-square is used as a criterion (Falk & Miller, 1992). For the Cute Numbers model the mean multiple R-square correlation was .23 (effect size f2 = .30) indicating a medium to large effect (Cohen, 1992: 157). The mean multiple R-square correlation for the Birthday Cake model was .20 (effect size f2 = .25) indicating a medium strength effect size (Cohen, 1992: 157). Thus reasonable stability in the estimation of the models was indicated and a sound explanatory effect signified.
3.3. Criterion Variable Pscore (Problem Solving Score)
Table 2 records the direct and indirect effects on the criterion variable Pscore for each latent variable, grouped by dimension and construct in the model. There were 11 variables having a direct effect on Pscore in the Cute Numbers example but only six variables in the Birthday Cake case. Of the variables with direct effects, 10 of them also contributed an indirect effect in the Cute Numbers model and four of them in the Birthday Cake model. Further, five variables had sole indirect effects in the Cute Numbers problem with 10 variables having sole indirect effects in the Birthday Cake problem. Three latent variables had no effect on Pscore in the Cute Numbers case and three variables had no effects on Pscore in the Birthday Cake example. The predictor variables explained 23 per cent of the variance for the Cute Numbers score and 30 per cent of the variance for the Birthday Cake score.
3.4. Patterns of Influence by Construct and Dimension
The pattern of influence for factors operating both directly and indirectly within the Cute Numbers and Birthday Cake models of creative problem solving is summarized in Table 3. The similarities and differences along with their interpretation are described below.
3.5. Antecedents
Within the Antecedent construct, the factors of (Gender), (Age) and school type (Stype) had both direct and indirect influence within the Cute Numbers model but only an indirect influence within the Birthday Cake model. This indicated that older girls who attended co-educational schools were more successful in the Cute Numbers case. However, a positive indirect effect for older boys who attended single sex schools was also observed.
3.6. Person Dimension
Within the Abilities construct, three-dimensional ability (Space3D) had both direct and indirect influences in each model. In addition, two-dimensional spatial ability (Space2D) had direct and indirect effects on achievement in the Cute Numbers model while an indirect effect only was observed in the Birthday Cake model. This suggested that demand for visual spatial processing was higher within the Cute Numbers model. Further verbal ability (Verbal) had only an indirect effect in each model although this influence was stronger within the Birthday Cake case.
Within the Perseverance and Motivation construct, play with novel mathematics problems and games (Play)

Table 2. Latent variables grouped by dimension and construct showing direct and indirect effects on Pscore (Problem solving score).

Table 3. Factors of direct and indirect influence within the Cute Numbers and the Birthday Cake models of creative problem solving.
had both a direct and indirect influence on successful problem-solving in the Cute Numbers case while an indirect effect only was observed for the Birthday Cake case. Further intrinsic motivation (Motiv) had both direct and indirect effects on achievement in the Birthday Cake case but only an indirect effect in the Cute Numbers case. Thus students who continued to persevere with the problem in the Birthday Cake case were more likely to be successful than those who did not. In addition an indirect effect of flow (L-flow) was in operation within the Cute Numbers model, while an indirect effect of novelty (Novel) was in operation within the Birthday Cake case. This indicated that students in the Cute Numbers model were more likely to experience flow than those in the Birthday Cake case. Further successful problem-solvers in the Birthday Cake case were more likely to have rated the problem as being less novel than successful problem solvers in the Cute Numbers example.
3.7. Environment Dimension
Within the Experiences construct (subset, Opportunity to Learn), the factors of prior practice (Priprac) and participation (Partic) had a direct and indirect effect in each model. Interpretation of these factors revealed that students in both models with experience in past Mathematics Challenge events are more likely to be successful than those without such experience and that lack of prior practice with Mathematics Challenge type problems was only useful if it was also accompanied with previous participation in Mathematics Challenge events. Further a negative indirect effect of resources (Aids) was in evidence within the Cute Numbers model. Thus students who performed well in the Cute Numbers case were likely to rely less heavily on Mathematics Challenge resources than successful students within the Birthday Cake case.
3.8. Process Dimension
Central to the findings of this study is the Approaches to Reasoning construct where an interesting pattern of cognitive and non-cognitive factors have emerged. Within the Birthday Cake model of creative problem solving, the cognitive elements of Systematic (Syst) and Strategic (Strat) approaches to reasoning had a direct effect within the model, while the non-cognitive elements of Feeling (Feel) and Free-flowing (Free) approaches to reasoning had an indirect effect. This finding is contrasted with the Cute Numbers case where the non-cognitive elements of Feeling (Feel) and Free-flowing (Free) approaches to reasoning had a direct effect while the cognitive element Strategic approach to reasoning (Strat) had an indirect effect within the model. Further, although a negative direct effect was observed for the Spatial-verbal factor (Spat/Vb) in the Cute Numbers case, a positive indirect effect for Spat/Vb was also found. A positive indirect effect for Spat/Vb was also present in the Birthday Cake case.
4. Discussion and Conclusion
This study began by asking three questions. The first question, that related to the kinds of cognitive and non cognitive approaches that middle school students’ use, when solving novel mathematics problems, may be answered by stating that the kind of approaches employed likely depends on the nature of the problem being solved.
Comparative findings indicate that different processes are at work within the Cute Numbers and Birthday Cake models. This is not only indicated by different spatial and verbal processing requirements demanded of each case but also by different reasoning approaches being utilized for successful solution in each problem. While good three-dimensional spatial ability is a predictor of successful solution for each model, the additional direct effect of good two-dimensional spatial ability in the Cute Numbers case, signifies the involvement of additional visual-spatial processing within the Cute Numbers problem. The non-cognitive processing elements of Free-flowing and Feeling approaches to reasoning are primarily involved within the Cute Numbers case while the cognitive processing element of the Systematic approach to reasoning and the Strategic approach to reasoning are primarily involved within the Birthday Cake case.
Importantly students who successfully solve the Cute Numbers problem make explicit use of non-cognitive processes characterized by the Free-flowing (Free) and Feeling (Feel) approaches to reasoning while students who successfully solve the Birthday Cake problem make explicit use of cognitive processes characterized by the Systematic (Syst) approach to reasoning.
The second question, concerning the manner in which cognitive and non-cognitive systems interact when solving novel mathematics problems, may be answered by stating that cognitive and non-cognitive systems likely interact through feeling guided by the intuitive function. This conclusion is reached by observing that even although the Birthday Cake problem is dominated by cognitive processing, the use of the non-cognitive factors Free (Free-flowing approach) and Feel (Feeling approach) are also in evidence. In particular, an indirect effect of Feel on Pscore (Problem score), operating through Syst (Systematic approach) is observed and an indirect effect of Free on Pscore operating through Feel and Syst is also present. This indicates that although the cognitive Systematic approach dominates the problem solving process the finding of a successful solution is not independent of the non-cognitive Feeling approaches. Further, it is observed that while the path from Strat (Strategic approach) to Pscore is negative, the path from Strat to Pscore passing through Feel is positive. This signifies that students who solve the Birthday Cake problem directly employing the cognitive Strategic approach to reasoning without recourse to a Feeling approach do not do so successfully.
The third question, regarding what relationships exist among cognitive and non-cognitive approaches to reasoning and success in novel mathematics problem solving, may be answered by stating that successful cognitive approaches to reasoning are likely dependent on non-cognitive ones. While novel problems can be solved successfully with a direct effect of feeling, no such problems are likely to be solved cognitively independent of feeling.
This conclusion is supported by the finding that although the Birthday Cake problem is characterized by direct effects of cognitive factors and by indirect effects of non-cognitive factors the reverse is not the case in the Cute Numbers problem. While the direct effects of non-cognitive factors characterize the Cute Numbers problem, the indirect effects of cognitive factors do not. Indeed, the factor for the Systematic approach to reasoning (Syst) plays no role at all in the successful solution of the Cute Numbers problem. Moreover, an indirect effect of the Strategic approaches to reasoning (Strat), operating through the non-cognitive factor Free is observed. This is also supported by an indirect effect of Free operating through Feel. Further, a negative direct effect for the Spatial-verbal approach to reasoning (Spat/Vb) is observed in the Cute Numbers problem. However a positive indirect effect of Spat/Vb operating through Feel is also present. This indicates that spatial-verbal processing, occurring without recourse to the Feeling approach to reasoning, is also unsuccessful.
Lastly a discussion of findings is not complete without making mention of the study’s limitations. Use of PLSPATH analyses permitting the exploratory observation of both direct and indirect effects, comes at the cost of a confirmatory procedure. Consequently running this data set in confirmatory SEM software is the logical next step. Further, if more schools had been available multi level work involving the interaction of student, classroom, teacher and school level factors on novel problem solving could have been undertaken. However, obtaining data from among the adolescent school group was seen as having greater relevance in a study where the role of feeling and intuition in novel mathematics problem solving was of central concern.
As a final point the question may be put “What are the implications for learning, teaching and guidance counseling?” Firstly, it may be asserted that feeling matters more than initially realized. In this study, taking into consideration both direct and indirect effects, no model of solution is found that is independent of a Feeling approach to reasoning. Secondly, there are different kinds of feeling. Attending to background feeling, is likely to provide useful guidance in solving a novel problem successfully than through the ignorance of it. In similar vein, it may be hypothesised, that failure to attend to some larger universal emotions (e.g. fear, anger) in a timely manner may result in the background feelings and skilled intuiting, needed for successful solution, not being heard or realised. Thirdly, efficiency in learning and teaching is likely not obtained by cutting straight to the cognitive content devoid of affect. Thinking well, this study shows, requires attending to both cognitive and non-cognitive components. Hence, educators and guidance counselors, along with those they teach and mentor will do well to engage directly and indirectly, with non-cognitive as well as cognitive approaches to reasoning in order that better and more effective solutions may be found.