Received 8 November 2015; accepted 23 May 2016; published 26 May 2016

1. Introduction
Let , then the matrix equation in the following form, can be called “linear matrix equation”:
, then the matrix equation in the following form, can be called “linear matrix equation”:
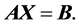 (1)
(1)
Matrix equations are arisen in control theory, signal processing, model reduction, image restoration, ordinary and partial differential equations and several applications in science and engineering. There are various approaches either direct methods or iterative methods to evaluate the solution of these equations [1] - [6] .
The HPM that was proposed first time by Doctor He [7] - [9] , was further developed by scientists and engineers. This general strategy which is a combination of the customary perturbation method and homotopy in topology, deforms to a simple problem which can be easily solved uninterruptedly. Moreover, HPM which does not involve a small parameter in an equation, has a significant advantage that it provides an analytical approximate solution to a wide range of either linear or nonlinear problems in applied sciences. In most cases, employing HPM gives a very speedy convergence of the solution series, and usually only a few iterations to acquire very accurate solutions are required, particularly when the improved version will be applied.
In terms of linear algebra, Keramati [10] first applied a HPM to solve linear system of equations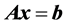 . The splitting matrix of this method is only the identity matrix. However, this method does not converge for some systems when the spectrum radius is greater than one. To make the method available, the auxiliary parameter and the auxiliary matrix were added to the homotopy method by Liu [11] . He has adjusted the Richardson method, the Jacobi method, and the Gauss-Seidel method to choose the splitting matrix. Edalatpanah and Rashidi [12] focused on modification of (HPM) for solving systems of linear equations by choosing an auxiliary matrix to increase the rate of convergence. Furthermore, Saeidian et al. [13] proposed an iterative method to solve linear systems equations based on the concept of homotopy. They have shown that their modified method presents more cases of convergence. More recently, Khani et al. [14] have combined the application of homotopy perturbation method and they have used use of different
. The splitting matrix of this method is only the identity matrix. However, this method does not converge for some systems when the spectrum radius is greater than one. To make the method available, the auxiliary parameter and the auxiliary matrix were added to the homotopy method by Liu [11] . He has adjusted the Richardson method, the Jacobi method, and the Gauss-Seidel method to choose the splitting matrix. Edalatpanah and Rashidi [12] focused on modification of (HPM) for solving systems of linear equations by choosing an auxiliary matrix to increase the rate of convergence. Furthermore, Saeidian et al. [13] proposed an iterative method to solve linear systems equations based on the concept of homotopy. They have shown that their modified method presents more cases of convergence. More recently, Khani et al. [14] have combined the application of homotopy perturbation method and they have used use of different 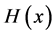 for solving system of linear equations. They mentioned that this modification performs better than the Homotopy Perturbation Method (HPM) for solving linear systems.
for solving system of linear equations. They mentioned that this modification performs better than the Homotopy Perturbation Method (HPM) for solving linear systems.
According to our knowledge, nevertheless HPM has not been modified to solve a matrix equation. In this survey, the main contribution is to suggest an improvement of the HPM for finding approximated solution for (1). Moreover, the necessary and sufficient conditions for convergence of the modified method will be investigated. Finally, some numerical experiments and applications are drawn in numerical results.
2. Solution of the Linear Matrix Equation
In this section, first the conditions that Equation (1) has a solution are decelerated. Then, some applicable relations by utilizing HPM will be attained. Eventually, convergence of HPM series will be analyzed in detail.
2.1. Existence and Uniqueness
The following theorems characterize the existence and uniqueness to the solution of Equation (1).
Theorem 2.1. [15] The linear matrix Equation (1) has a solution if and only if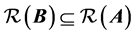 . Equivalently, a solution exists if and only if
. Equivalently, a solution exists if and only if , whereas
, whereas  is denoted a Moore-Penrose pseudo-inverse of matrix
is denoted a Moore-Penrose pseudo-inverse of matrix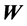 .
.
Theorem 2.2. [15] Let ,
, 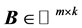 and suppose that
and suppose that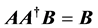 . Then any matrix in the form
. Then any matrix in the form
 (2)
(2)
is a solution of (1), where  is arbitrary matrix. Furthermore, all solutions of Equation (1) are in this form.
is arbitrary matrix. Furthermore, all solutions of Equation (1) are in this form.
Theorem 2.3. [15] A solution of the matrix linear Equation (1) is unique if and only if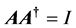 . Alternatively, (1) has a unique solution if and only if
. Alternatively, (1) has a unique solution if and only if .
.
Remark 2.4. It should be emphasized that when ![]() is square and nonsingular matrix,
is square and nonsingular matrix, ![]() and so
and so![]() . Thus, there is no arbitrary component, leaving only the unique solution
. Thus, there is no arbitrary component, leaving only the unique solution![]() . Moreover, in the sense of linear algebra, avoiding the computation of matrix inversion is recommended because of increasing computational complexity.
. Moreover, in the sense of linear algebra, avoiding the computation of matrix inversion is recommended because of increasing computational complexity.
2.2. Homotopy Perturbation Method
Now, we are ready to apply the convex homotopy function in order to obtain the solution of linear matrix equation. A general type of homotopy method for solving (1) can be described by setting![]() , as follows. Let
, as follows. Let
![]() (3)
(3)
![]() (4)
(4)
A convex homotopy would be in the following form
![]() (5)
(5)
whenever, the homotopy ![]() is defined by
is defined by
![]() (6)
(6)
![]() (7)
(7)
Notice that F is an operator with known solution![]() . In this case, HPM utilizes the homotopy parameter p as an expanding parameter to obtain
. In this case, HPM utilizes the homotopy parameter p as an expanding parameter to obtain
![]() (8)
(8)
and it gives an approximation to the solution of (1) as
![]() (9)
(9)
By substituting (3) and (4) in (5), and by equating the terms with the identical power of p, after simplification and application of the relations, we obtain
![]() (10)
(10)
If take![]() , this implies that
, this implies that
![]() (11)
(11)
Hence, the solution can be expressed in the following form
![]() (12)
(12)
Remark 2.5. It should be pointed out that we have focused to the solution of matrix equation![]() , whenever all matrices are non square. But it is found that the homotopy function can not be constructed because of disagreement between dimension of matrices. This issue is presented in the following relation:
, whenever all matrices are non square. But it is found that the homotopy function can not be constructed because of disagreement between dimension of matrices. This issue is presented in the following relation:
![]()
Thus, we considered all matrices in Equation (1) are square.
2.3. Convergence Analysis
To verify whether the sequence ![]() in (12) is converge or not, we give following analysis. Notice that throughout the following theorems,
in (12) is converge or not, we give following analysis. Notice that throughout the following theorems, ![]() denotes the spectral radius which is defined by
denotes the spectral radius which is defined by![]() , whenever
, whenever ![]() is spectrum of the matrix
is spectrum of the matrix![]() .
.
Theorem 2.6. The sequence ![]() is a Cauchy sequence if
is a Cauchy sequence if
![]() (13)
(13)
Proof: It is clear that![]() . Then by taking matrix norm
. Then by taking matrix norm
![]()
Hence, if![]() , we have obviously
, we have obviously![]() , and then
, and then
![]()
Thus ![]() is a Cauchy sequence. This completes theorem. ,
is a Cauchy sequence. This completes theorem. ,
Definition 2.7. [16] A matrix ![]() is called strictly row diagonally dominant (SRDD), if we have
is called strictly row diagonally dominant (SRDD), if we have
![]() (14)
(14)
Theorem 2.8. Consider the matrix ![]() where
where ![]() are diagonal elements of matrix
are diagonal elements of matrix![]() . If the matrix
. If the matrix ![]() be SRDD, then we have
be SRDD, then we have
![]() (15)
(15)
Proof: Suppose ![]() and
and![]() , then it can be easily shown that
, then it can be easily shown that
![]()
Since ![]() is SRDD matrix, it is clear that
is SRDD matrix, it is clear that![]() . Hence,
. Hence,
![]()
Therefore,
![]()
which completes the proof. ,
In Theorem 2.8, the important question is “Does the matrix ![]() is SRDD whenever
is SRDD whenever ![]() and
and ![]() are SRDD matrices?” The answer of this question is negative. Because, firstly the product of two SRDD matrices is
are SRDD matrices?” The answer of this question is negative. Because, firstly the product of two SRDD matrices is
not SRDD, as a counterexample we can pay attention to the matrices ![]() and
and![]() , and their product is
, and their product is![]() . Secondly, inversion of SRDD matrix is not SRDD. As a counterexample, consider
. Secondly, inversion of SRDD matrix is not SRDD. As a counterexample, consider ![]() which has the inversion
which has the inversion![]() .
.
Now, if![]() , by pre-multiplying the both sides of Equation (1) by matrix
, by pre-multiplying the both sides of Equation (1) by matrix![]() , the following equation can be obtain:
, the following equation can be obtain:
![]() (16)
(16)
To be more precise, by using convex homotopy function, we can easily verify that
![]() (17)
(17)
In this part, we would like to show that the series ![]() is converges. Thus, first we need the following definition and theorems.
is converges. Thus, first we need the following definition and theorems.
Definition 2.9. [16] Let ![]() are three matrices satisfying
are three matrices satisfying![]() . The pair of matrices
. The pair of matrices ![]() is a regular splitting of
is a regular splitting of![]() , if
, if ![]() is nonsingular and
is nonsingular and ![]() and
and ![]() are nonnegative.
are nonnegative.
Theorem 2.10. Let ![]() is nonsingular matrix such that
is nonsingular matrix such that ![]() and
and ![]() are nonnegative. Then the sequence
are nonnegative. Then the sequence
![]() (18)
(18)
converges if ![]() is nonsingular and
is nonsingular and ![]() is nonnegative.
is nonnegative.
Proof: Suppose that ![]() is a singular matrix such that
is a singular matrix such that ![]() and
and ![]() are nonnegative. By employing Theorem 2.9 it can be obtain that
are nonnegative. By employing Theorem 2.9 it can be obtain that ![]() as both
as both ![]() and
and ![]() are a regular splitting of
are a regular splitting of![]() . This implies that
. This implies that
![]() (19)
(19)
is converges series. ,
3. Numerical Experiments
In this section, some numerical illustrations are provided. All computations have been carried out using MATLAB 2012 (Ra) with roundoff error![]() . Moreover, the error of the approximations have been measured by the following stopping criteria:
. Moreover, the error of the approximations have been measured by the following stopping criteria:
![]() (20)
(20)
whereas, ![]() is the approximated solution obtained by HPM.
is the approximated solution obtained by HPM.
Example 3.1. First example made approximating the solution of the equation ![]() by using modified HPM. In order to this purpose, two
by using modified HPM. In order to this purpose, two ![]() matrices A and B are considered:
matrices A and B are considered:
![]()
After evaluating the inversion of ![]() and multiplying by
and multiplying by![]() , it is observed that
, it is observed that ![]() is SRDD matrix, and thus the matrix
is SRDD matrix, and thus the matrix ![]() can be obtained as
can be obtained as
![]()
Furthermore,![]() . Hence, considering seven terms of homotopy series as:
. Hence, considering seven terms of homotopy series as:
![]()
the approximated solution could be obtained as follows:
![]()
However, the exact solution of ![]() is
is
![]()
In conclusion, it can be seen that the approximation has a good agreement with the exact solution. In this case the residual error is![]() .
.
Example 3.2. In this example, two ![]() strictly diagonally dominant matrices are assumed as follows:
strictly diagonally dominant matrices are assumed as follows:
![]()
The solution of matrix equation ![]() is approximated using HPM. The residual errors have been measured for different dimension of matrices and for different terms in homotopy method. Results are reported in Table 1. In this example, by increasing dimension of the matrices, the error of the approximation will be increased gradually. In addition, considering more terms of the homotopy method, the approximation will be more accurate.
is approximated using HPM. The residual errors have been measured for different dimension of matrices and for different terms in homotopy method. Results are reported in Table 1. In this example, by increasing dimension of the matrices, the error of the approximation will be increased gradually. In addition, considering more terms of the homotopy method, the approximation will be more accurate.
Example 3.3 (Application in matrix inversion). If we substitute ![]() in the matrix Equation (1), then we have
in the matrix Equation (1), then we have![]() . Thus, by applying the HPM to this equation, the inversion of matrix
. Thus, by applying the HPM to this equation, the inversion of matrix ![]() can be easily evaluated. For this purpose, assume the following
can be easily evaluated. For this purpose, assume the following ![]() matrix:
matrix:
![]()
This matrix is diagonally dominant and well conditioned matrix. We have used MATLAB command inv(A) with very small error ![]() (we considered as exact solution) and compare it with HPM calculation. Results are shown in Figure 1. It is obviously seen that the approximated solutions for different dimensions (N = 10, 20, 30, 40) are very close to the exact solutions.
(we considered as exact solution) and compare it with HPM calculation. Results are shown in Figure 1. It is obviously seen that the approximated solutions for different dimensions (N = 10, 20, 30, 40) are very close to the exact solutions.
4. Conclusion
In this work, the linear matrix equation is solved by improving the well-known perturbation method. Numerical experiments demonstrated that by considering more terms of the approximations, error will be decreased dramatically. Furthermore, if the matrix ![]() becomes more strictly row diagonally dominant, convergence of the homotopy series will increase. In conclusion, it is interesting to know that considering special case
becomes more strictly row diagonally dominant, convergence of the homotopy series will increase. In conclusion, it is interesting to know that considering special case![]() , the proposed method can compute inverse of the matrix
, the proposed method can compute inverse of the matrix ![]() efficiently. Moreover, the author found that this method could be generalized to obtain the solution of other equations.
efficiently. Moreover, the author found that this method could be generalized to obtain the solution of other equations.
Acknowledgements
Special thanks go to the anonymous referee for some valuable suggestions, which have resulted in the improvement of this work. This work is supported by Islamic Azad University, Robat Karim University, Tehran, Iran.
![]()
Table 1. Comparison error for different dimensions in Example 3.2.
![]()
Figure 1. Comparison error between MATLAB command and HPM for matrix inversion.
Conflict of Interests
The author declares that there is no conflict of interests regarding the publication of this article.