Shadow Detection Method Based on HMRF with Soft Edges for High-Resolution Remote-Sensing Images

Wenying Ge

School of Computer and Information Engineering, Anyang Normal University, Anyang, China.

DOI: 10.4236/jsip.2019.104011                

Abstract

Shadow detection is a crucial task in high-resolution remote-sensing image processing. Various shadow detection methods have been explored during the last decades. These methods did improve the detection accuracy but are still not robust enough to get satisfactory results for failing to extract enough information from the original images. To take full advantage of various features of shadows, a new method combining edges information with the spectral and spatial information is proposed in this paper. As known, edge is one of the most important characteristics in the high-resolution remote-sensing images. Unfortunately, in shadow detection, it is a high-risk strategy to determine whether a pixel is the edge or not strictly because intensity values on shadow boundaries are always between those in shadow and non-shadow areas. Therefore, a soft edge description model is developed to describe the degree of each pixel belonging to the edges or not. Sequentially, the soft edge description is incorporating to a fuzzy clustering procedure based on HMRF (Hidden Markov Random Fields), in which more appropriate spatial contextual information can be used. More concretely, it consists of two components: the soft edge description model and an iterative shadow detection algorithm. Experiments on several remote sensing images have shown that the proposed method can obtain more accurate shadow detection results.

Keywords

Shadow Detection, Soft Edges, Clustering, Remote-Sensing Images

1. Introduction

Remote sensing images are applied in many fields, including geography mapping, agriculture, change detection, etc. Unfortunately, shadows in these images obstruct these applications because of the reduction or even loss of radiance in the shadow areas. To detect shadows, early works extracted spectral features of shadow areas, such as lower intensity [1], higher saturation [2], large hue value and blow blue color value [3], etc. Later, in order to take full advantages of spectral features of multiband images, some researches explored invariant color spaces to stress the differences between shadows and non-shadows [4] [5] [6]. Also, some efforts on combining different spectral features [7] [8] have achieved some good results in their intended realms. However, there are still some limits in these methods because of the absence of other information such as edges and spatial context information.

As for spatial information, the well-known probabilistic model HMRF which serve as a powerful formal tool to present neighborhood interactions is a natural choice [9]. In recent years, many researchers have attempted to incorporate more information into it to improve the performance of HMRF [10] [11]. Our latest work [12] adds edge constraints into the iterative clustering procedure based on HMRF. In this work, an edges consistency model is proposed to describe the similarity between the clustering edges and the pre-detected ones. This method can obtain more clear boundaries along with the homogeneous area. However, it is not a good idea to determine whether a pixel is the edge or not strictly because the spectral features of pixels on the shadow boundaries are not discriminable enough.

In this paper, a soft edge model is raised to present the probability of a pixel being considered as an edge pixel. Thus, pixels with lower probability should be labeled according its spectral features and the neighbor interaction, which tend to obtain more homogeneous area. Comparatively, label assigned to pixels which have higher edge probability should lead to more clear boundaries. It means that we should balance the influence of different pixels in the iterative procedure. So, there came a new object function, which is defined to ensure that different roles are assigned to more likely edge pixels and the other ones. Given all that, there are two main contributions in this paper. One is the soft edge model, and the other is a new object function based on which an iterative shadow detection method is proposed.

This paper is organized as follows. In Section 2, we will describe the soft edge model and the proposed clustering method with edge constraints, which followed by the analysis of experiments on remote sensing images in Section 3. Finally, conclusions are drawn in Section 4.

2. Shadow Detection Method with Soft Edges

2.1. Soft Edges Model

As mentioned in section 1, a natural way to describe shadow edges is using the soft manner. Therefore, an essential indicator must be defined to measure the probability of pixels being considered as shadow edges.

Let Y denote an intensity image defined on a $m\times n$ rectangular lattice set, $s=\left\{1,2,\cdots ,S\right\}$ denote the set of pixel sites. Then the corresponding shadow image can be defined as $X=\left\{x_i|x_i=0,1;i\in s\right\}$ , in which, 0 is the label for non-shadows while 1 is for shadows.

Edges typically are detected according gradient. Pixels with larger gradient should be considered as edges. Therefore, many researches explored shadow detection method using threshold of gradient. Taking “Canny edge detection” as example, two thresholds of gradient are used to determine whether a pixel is an edge one or not. We can introduce these two thresholds into the soft edges model, shown as:

$g_i=\{\begin{array}{l}1gra{d}_i>{\theta }_l\\ \frac{gra{d}_i}{{\theta }_l}\text{otherwise}\\ 0gra{d}_i<{\theta }_s\end{array}$ (1)

In which, $gra{d}_i$ is the gradient of pixel, ${\theta }_l$ is the larger threshold in Canny detection while ${\theta }_s$ is the small one. Therefore, $g_i$ indicate the degree of pixel belonging to an edge in view of gradient.

In actual images, not all pixels with higher gradient value are true edges, for example, noises. To exclude this, a shadow detection using intensity features will be employed as the initial detection and then neighbor pixels would be exploited. Generally, neighbors of a noise pixel belong to the same class, which means they should have the same label. In other words, the more shadow neighbors a pixel has, the lower edge probability it should be assigned. Aiming at achieving an edge probability for each pixel, the soft edge indicator should take the two terms into account.

So, the indicator can be defined as:

$e_i=g_i+\alpha \frac{N-{\displaystyle {\sum }_{j\in {\partial }_i}\left(x_j=0\right)}}{N}$ (2)

where ${\partial }_i$ denote the neighborhood of i^th pixel while N is the number of the neighbors. $\alpha$ is a factor who can balance the power of two terms.

2.2. Shadow Detection Method with Soft Edges

Aiming at partitioning an image into shadow areas and non-shadow areas, the procedure of shadow detection can be treated as a process of image labeling. As known, HRMFs can be found in most image labeling methods for the excellent capability of spatial description. At the same time, Fuzzy C-means (FCM) clustering is also one of the most widely used algorithms which can retain enough information from the original images compared to threshold methods. Hereby, HMRF-FCM [13] combining the benefits of HMRF and FCM to deal with the fuzziness and region homogeneity of the labeled images becomes a natural choice.

HMRF-FCM incorporates the HMRF into FCM by understanding HMRF in a fuzzy way. It treats kth HMRF models as a fuzzy classification. The fuzzy classification is defined as:

$R=\left\{u_{ik}\right\}$

in which, $u_{ki}$ denotes the membership of i^th pixel to the k^th cluster ( $k=\left\{0,1\right\}$ in our shadow detection task). And an iterative procedure is carried out to updating the membership matrix. Our proposed soft edge model is employed in the iterative updating procedure to impose edge constraints. As mentioned above, labels of edge pixels should lead to more accurate boundaries while that of shadow ones should be of benefit to region homogeneity.

Considering that boundaries generally are continuous along a certain direction, a novel membership is defined as:

$b_{ki}=\frac{{\displaystyle {\sum }_{p\in {\partial }_i^s}\delta \left(x_i,x_p\right)}}{{\displaystyle {\sum }_{x_i=1}^k{\displaystyle {\sum }_{p\in {\partial }_i^s}\delta \left(x_i,x_p\right)}}}$ (3)

In which, ${\partial }_i^s$ denotes neighborhoods of ith pixel along direction s. $\delta (·)$ is a function denoted as:

$\delta \left(x,y\right)=\{\begin{array}{cc}1& x=y\\ 0& x\ne y\end{array}$

According Equation (3), along direction s, the more same labeled neighbors the pixel has, the larger value be assigned to $b_{ki}$ . In other words, it is also a membership of i^th pixel to the k^th cluster. But the main consideration about $b_{ki}$ is that the label k given to i^th pixel should make the pixel have more same labeled neighbors along one direction. The direction s is determined by:

$s=\arg {\max }_{s=1}^4{\displaystyle {\sum }_{p\in {\partial }_j^s}\delta \left(x_i,x_p\right)}$ (4)

Based on this, the objective function of this iterative clustering procedure can be defined as:

$J_m={\displaystyle \underset{k=1}{\overset{K}{\sum }}{\displaystyle \underset{i=1}{\overset{S}{\sum }}\left(1-e_i\right)u_{ki}{d}_{ki}}}+{\displaystyle \underset{k=1}{\overset{K}{\sum }}{\displaystyle \underset{i=1}{\overset{S}{\sum }}{e}_i{r}_{ki}{d}_{ki}}}+\lambda {\displaystyle \underset{k=1}{\overset{K}{\sum }}{\displaystyle \underset{i=1}{\overset{S}{\sum }}{u}_{ki}\log \left(\frac{u_{ki}}{{\pi }_{ki}}\right)}}$ (5)

in which,

$d_{ki}=-\log p\left(y_i|x_i=k;{\theta }_i\right)$ (6)

And ${\pi }_{ki}$ is the pointwise prior probabilities of the HMRF model states, which can be denoted as:

${\pi }_{ki}\triangleq P\left(x_i=k|{\tilde{x}}_{N_i};\beta \right)=\frac{\exp \left(-{{\displaystyle \sum }}_{i\in c}{V}_c\left({\tilde{x}}_{ki}|\beta \right)\right)}{{{\displaystyle \sum }}_{h=1}^K\exp \left(-{{\displaystyle \sum }}_{i\in c}{V}_c\left({\tilde{x}}_{hi}|\beta \right)\right)}$ (7)

To sum up, the proposed algorithm for shadow detection comprises the following steps.

1) Get the detected edge image $\epsilon =\left\{{\epsilon }_i|{\epsilon }_i=\left\{0,1\right\}\right\}$ by edge detection method

2) Initialize the membership matrix $\left\{u_{ki}^{\left(1\right)}\right\}$ by the original FCM algorithm, and derive the mean ${\mu }_k^1$ and the standard deviation ${\sigma }_k^{(1)}$

3) Estimate the label field $\left\{x_i^{\left(t\right)}\right\}$ by defuzzification.

4) Compute the edge probability matrix $\left\{e_i^{\left(t\right)}\right\}$ .

5) Compute the membership matrix $\left\{b_{ki}^{\left(t\right)}\right\}.$

6) Get the pointwise prior probabilities according Equation (7).

7) Compute the distance matrix $\left\{d_{ki}^{\left(t\right)}\right\}$ that is given by Equation (6).

8) Update the membership matrix $\left\{u_{ki}^{\left(t+1\right)}\right\}$ , the mean $\left\{{\mu }_k^{t+1}\right\}$ and the standard deviation $\left\{{\sigma }_k^{\left(t+1\right)}\right\}$ .

9) If it converge then stop, otherwise, set 𝑡 = 𝑡 + 1 and go to step 3).

3. Experiments and Analysis

3.1. Data

To evaluate the performance of proposed shadow detection method, we chose three pieces of remote sensing urban images among which the main variation is the complexity of scenes contents (Figures 1-4).

Image 1: The first image is acquired in September 2003, refers to a 280 × 280 pixel image in the visible spectrum. As shown in Figure 1, it mainly consists of grass areas, buildings, and their shadows.

Image 2: Beijing in May 2011. The second image is scene of Beijing acquired in May 2011 and its size is 300×300. It mainly contains trees, grass, buildings, blue roofs, and shadows.

Image 3: Beijing in April 2011. The second image is scene of Beijing acquired in May 2011 and its size is 300×300. The land covers in it are same with Image 2, except for roads.

Figure 1. First image.

Figure 2. Bejing in May 2011.

Figure 3. Beijing in April 2004.

Figure 4. Wuhan University in 2004.

Image 4: Wuhan University in 2004. The fourth image represents a crop of 256 × 256 pixels of the Wuhan University acquired in 2004. There are six land covers: roads, bared land, trees, buildings, water, and shadows.

3.2. Compression Approaches

To verify the superiority of the proposed shadow detection method to the ones without edge constraints, three methods are employed as the competitors: bithreshold method [7], PCAHSI [8], and soft Shadow Detection method [12].

Bithreshold method

Bithreshold method tries to use two spectral features of shadow areas. Firstly, transform the image into HIS color space, compute the normalized difference of intensity (𝐼) and saturation (𝑆) components, and obtain the initial detection by its threshold. Then, get the detection result of 𝐼 channel by histogram threshold. The final result is obtained by performing AND operation on two detected results mentioned above.

PCAHSI

Firstly, compute the shadow index (SI) based on principal component transformation and HIS model. Then, image is divided into the shadow area and nonshadow area by SI histogram threshold.

Soft shadow

This method introduces the concept of opacity of image matting into shadow detection and puts forward a new concept of shadow probability. Firstly, compute the shadow probability according the intensity and opacity. Then this probability is employed as the class conditional probability and an iterative procedure based on MRF is used to segment the image into shadow areas and the nonshadows.

3.3. Experiments and Discussion

In this section, the performance of the proposed method is verified by experimental results. Some parameters in our experiments were chosen empirically. In detail, 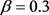for Potts model and $\alpha =0.2$ for soft edge indicator. Another important parameter, the window size of neighborhood for HMRF is set as 3 × 3 because it can preserve as much as possible the image details.

Visual Comparison

Experimental results on the first image using different methods (bi-threshold, PCA method, soft shadow method, the proposed method) are shown in Figure 5. Figure 5(e) is the ground truth of image 1.

Obviously, there are many misdetection in Figure 5(a) and Figure 5(b) because these two methods only used thershold of spectual features. It is not efficient enough to distinguish dark objects from shadows. These defects are removed in soft shadow method shown in Figure 5(c), which thanks for the soft shadow model. Also because of the use of HMRF, soft shadow method obtained more homogenous regions. But, region boundaries in Figure 5(c) are so smooth that some details are missing, even some trivial shadow areas. Seen from Figure 5(d), the proposed method is superior to the competitive ones. It can obtain more accurate boundaries as well as homogenous regions for the constrainsts of edgs. These comparisons can also be presented in Figure 6, Figure 7 and Figure 8. From the comparison of results of four images, we can see that as the complexity

(a) (b) (c) (d) (e)

Figure 5. Detection results of Image 1. (a) Bi-threshold; (b) PCA; (c) Soft shadow; (d) The proposed method; (e) The ground truth.

(a) (b) (c)(d) (e)

Figure 6. Detection results of Image 2. (a) Bi-threshold; (b) PCA; (c) Soft shadow; (d) The proposed method; (e) The ground truth.

(a) (b) (c)(d) (e)

Figure 7. Detection results of Image 3. (a) Bi-threshold method; (b) PCA method; (c) Soft shadow method; (d) The proposed method; (e) The ground truth.

(a) (b) (c)(d) (e)

Figure 8. Detection results of Image 4. (a) Bi-threshold method; (b) PCA method; (c) Soft shadow method; (d) The proposed method; (e) The ground truth.

Table 1. Recall and precision.

of land covers increases, the greater misdetection occurs.

Quantitative Comparisons

To obtain a quantitative comparison between different algorithms, both recall and precision are employed as the performance metrics. Recall represents how many true shadow pixels have been detected as shadow pixels, which is denoted by

$DR=\frac{N_c}{N_t}\times 100\%$ (8)

where $N_t$ is the number of true shadow pixels, while $N_c$ is the number of pixels detected as shadows correctly. $N_c$ is computed by performing AND operation on the detected result and the true shadow mask.

Precision indicates that in the detected shadow pixels, how many correct ones are there. It can be denoted as:

$DP=\frac{N_c}{N_d}\times 100\text{\%}$ (9)

where $N_d$ is the number of pixels labeled as shadow. From the definition, it is easy to conclude that the recall favors over detection and the precision favors under detection. That is to say, high recall combined with a low precision means over detection shadows. We measured the recall and precision of each method and listed their values in Table 1. From the quantitative results as shown in Table 1, it is easy to conclude that the proposed method can obtain more accurate shadow detection results than the competitors.

4. Conclusion

In this paper, in order to add edge constraints into shadow detection, a soft edge model is put forward, considering the fact that shadow edges are not discriminate clearly. Based on this, an iterative shadow detection method with edge constraints based on HMRF is proposed. Experiments on remote sensing images have illustrated that the proposed method can get more clearly edges as well as homogenous regions.

Funding

This work is supported in part by the National Natural Science Foundation of China under Grants 41001251, the Key Technology Projects of Henan province of China (No. 132102210212), the Key Technology Projects of the Educational Department of Henan Province of China (No. 16A520036).

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Jaynes, C., Webb, S., Steele, R.M., Brown, M. and Seales, W.B. (2001) Dynamic Shadow Removal from Front Projection Displays. Proceedings of the IEEE Conference on Visualization, San Diego, CA, 21-26 October 2001, 175-182. https://doi.org/10.1109/VISUAL.2001.964509
[2]	Polidorio, A.M., Flores, F.C., Imai, N.N., Tommaselli, A.M.G. and Franco, C. (2003) Automatic Shadow Segmentation in Aerial Color Images. Proceedings of the 16th Brazilian Symposium on Computer Graphics and Image Processing, Sao Carlos, 12-15 October 2003, 270-277. https://doi.org/10.1109/SIBGRA.2003.1241019
[3]	Huang, J., Xie, W. and Tang, L. (2004) Detection of and Compensation for Shadows in Colored Urban Aerial Images. Proceedings of the 5th World Congress on Intelligent Control and Automation, June 2004, 3098-3100.
[4]	Ma, H.J., Qin, Q.M. and Shen, X.Y. (2008) Shadow Segmentation and Compensation in High Resolution Satellite Images. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, 7-11 July 2008, 1036-1039.
[5]	Arevalo, V., Gonzalez, J. and Ambrosio, G. (2008) Shadow Detection in Color High-Resolution Satellite Images. International Journal of Remote Sensing, 29, 1945-1963. https://doi.org/10.1080/01431160701395302
[6]	Tsai, V.J.D. (2006) A Comparative Study on Shadow Compensation of Color Aerial Images in Invariant Color Models. IEEE Transactions on Geoscience and Remote Sensing, 44, 1661-1671. https://doi.org/10.1109/TGRS.2006.869980
[7]	Yang, J., Zhao, Z. and Yang, J. (2008) A Shadow Removal Method for High Resolution Remote Sensing Image. Geomatics and Information Science of Wuhan University, 33, 17-20.
[8]	Liu, H. and Xie, T. (2013) Study on Shadow Detection in High Resolution Remote Sensing Image of PCA and HIS Model. Remote Sensing Technology and Application, 28, 78-84.
[9]	Ngo, T.T., Collet, C. and Mazet, V. (2015) MRF and Dempster-Shafer Theory for Simultaneous Shadow/Vegetation Detection on High Resolution Aerial Color Images. Traitement du Signal, 32, 5037-5041. https://doi.org/10.1109/ICIP.2014.7026020
[10]	Wang, C., Liu, J., Gong, M., Jiao, L. and Liu, J. (2014) Fuzzy c-Means Clustering with Weighted Energy Function in MRF for Image Segmentation. 2014 IEEE International Conference on Fuzzy System (Fuzzy-IEEE), Beijing, 6-11 July 2014, 210-215. https://doi.org/10.1109/FUZZ-IEEE.2014.6891657
[11]	Liu, G., Zhang, Y. and Wang, A. (2015) Incorporating Adaptive Local Information into Fuzzy Clustering for Image Segmentation. IEEE Transactions on Image Processing, 24, 3990-4000. https://doi.org/10.1109/TIP.2015.2456505
[12]	Ge, W.Y. and Liu, G.Y. (2018). Unsupervised Classification of High-Resolution Remote-Sensing Images under Edge Constraints. Pattern Recognition and Computer Vision. https://doi.org/10.1117/12.2285777
[13]	Chatzis, S.P. and Varvarigou, T.A. (2008) A Fuzzy Clustering Approach toward Hidden Markov Random Field Models for Enhanced Spatially Constrained Image Segmentation. IEEE Transactions on Fuzzy Systems, 16, 1351-1361. https://doi.org/10.1109/TFUZZ.2008.2005008