1. Introduction
The productivity of an organization is very much affected by the type of layout and the design of the layout used. In reality, there are four different layouts, viz. process layout, product layout, cellular layout and fixed position layout. The cellular layout combines the benefits of process layout and product layout. In this paper, the cellular layout is considered.
The objective of the cellular layout design is to group a given number of components which uses a set of machines into a distinct machine-component cells such that the processing requirements of the components assigned to each machine cell are fully met within that cell itself. This problem comes under combinatorial category. Hence, the usage of heuristics is inevitable.
Several methods have been developed to solve this cell formation problem, like mathematical programming approach (Mahdavi et al. [1] , Khaksar-Haghani et al. [2] , Arkat et al [3] ), meta-heuristic approach includes Genetic Algorithm (GA) (Saeedi et al [4] , Banerjee and Das [5] , Arkat et al [6] , Yin and Khoo [7] , Ozcelik and Sarac [8] , Sarac and Ozcelik [9] ), Simulated Annealing (SA) (Wu et al. [10] , Lin et al. [11] , Paydar et al. [12] , Kia et al. [13] ) and Hybrid heuristics (Rezaeian et al. [14] , Ghezavati and Saidi-Mehrabad [15] , Elbenani and Ferland [16] , Rafiei and Ghodsi [17] , Paydar and Saidi-Mehrabad [18] , Dalfard [19] ). Nevertheless, the complexity of the problem and the significant issues involved in obtaining the result create necessity for more effective algorithms.
In this paper, a hybrid genetic algorithm is developed to obtain machine-component cells to maximize each of the measures, viz. grouping efficiency and grouping efficacy.
2. Literature Review
As there are many methodologies to solve machine-component cell formation problem, generating a meaningful machine groups and component families using an algorithm gives a good start to obtain the best solution. Srinivasan and Narendran [20] proposed a non-hierarchical clustering algorithm in which initial seed is generated by maximum density rule. Srinivasn [21] used minimum spanning tree (MST) method to identify the initial seed for the machine-component cell formation problem from the given machine-component incidence matrix. A comparative study is carried out by Miltenburg and Zhang [22] and reported that the quality of the solution obtained by the seed generation algorithms is better than that of ROC (Rank Order Cluster) algorithm, SLINK or ALINK. Kao and Li [23] initially generated component seeds by applying the ant colony recognition algorithm and used the seed to obtain a complete block diagonal matrix. Nambirajan and Panneerselvam [24] developed a simulated annealing algorithm for the machine-component cell formation problem and compared its results with a set of existing algorithms and found that their algorithm surpassed the other algorithms in terms of grouping efficiency as well as grouping efficacy.
The genetic algorithm proposed by Holland [25] has applications in optimization of different problems of reality. Its application has been formalized by Goldberg [26] . This method is further implemented by Venugopal and Narendran [27] to handle multi-objective cell formation problem in which the volume of inter-cell moves and the total within cell moves are minimized. Balakrishna and Jog [28] initially formed the similarity index matrix and then proposed parallel genetic algorithm to solve the cell formation problem. Joines et al. [29] , Su and Hsu [30] and Mahdavi et al. [31] proposed a mathematical model and then implemented a genetic algorithm to minimize the inter-cell moves. Many researchers (James et al. [32] , Kelling et al. [33] and Tunnukij and Hicks [34] ) developed hybrid-genetic algorithm and measured the quality of the machine-component cell formation by grouping measures, viz. grouping efficiency, grouping efficacy, grouping index, etc. Tariq et al. [35] and Pailla et al. [36] applied genetic algorithm (GA) with local search heuristic (LSH) to maximize the machine utilization and to minimize the inter-cell moves. Banerjee and Das [5] investigated the cell formation problem by Predator-Prey Genetic Algorithm by local selection strategy. Sarac and Ozcelik [9] introduced three different selection and crossover operations and tested the performance of proposed algorithm with an existing algorithm using 15 test problems. Vin and Delchambre [37] defined the generalized cell formation problem and developed a grouping genetic algorithm to solve it. Li et al. [38] developed a genetic algorithm for virtual cell reconfiguration problem. Deep and Sing [39] designed a cellular manufacturing system for a dynamic environment. They first developed a mathematical model for this problem and then developed a genetic algorithm to solve this problem.
Among different algorithms reviewed in this paper, the genetic algorithm is considered for further improvement, because the population used in this algorithm consists of chromosomes whose genes are generated randomly. This amounts to searching the entire solution space of the machine-component cell formation problem.
3. Problem Definition
Let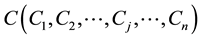 
be the set of components to be manufactured and 
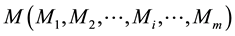be the set of machines which are required to manufacture the given set of components. Here, n is the total number of component types and m is the total number of machine types.
Let
, if the component j requires processing on machine i;
= 0, otherwise.
for 
and
.
A sample machine-component incidence matrix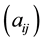 
is shown in Figure 1. The rearrangement of rows and columns of this matrix gives an alternate form of machine-component incident matrix as shown in Figure 2.
The machine-component incidence matrix shown in Figure 1 consists of 5 machines and 7 components. This is converted to a form as shown in Figure 2, which shows a block diagonal form with two odd elements in the off-diagonal blocks. This solution has two machine-component cells. The machines 1 and 4 and the components 6, 2 and 4 form the machine-component cell 1. Similarly the machines 2, 3 and 5 and the components 5, 7, 1 and 3 form the machine-component cell 2. From Figure 2, it is clear that there are two exceptional elements, which are with respect to machine 3 and component 6 and machine 1 and component 5. So, the exceptional element of component 6 should be processed in machine-component cell 2, because the machine 3 is assigned to it. Similarly the exceptional elements of component 5 should be processed in machine-component cell 1. In this process, the component 6 as well as the component 5 moves to another cell to process missing operation. Such movements between machine-component cells are called inter-cell moves which should be minimized
The objective of the design of the cellular layout is to obtain a block diagonal form such that the desired measures of performance are optimized. The grouping efficiency and grouping efficacy are the well known measures of performance of the cellular layout, whose formulas are as given below.
The grouping efficiency is introduced by Chandrasekharan and Rajagopalan [40] [41] to define the quality of the solution, named as grouping efficiency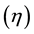
, which is the weighted sum of two functions as given below.
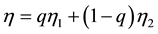
where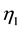 
is the ratio of number of 
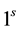in the diagonal blocks to the total number of elements in the diagonal blocks.
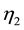is the ratio of number of 
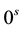in the off-diagonal blocks to the total number of elements in the off-di- agonal blocks.
is a weighting factor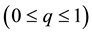 
and it is usually assumed as 0.5.
Kumar and Chandrasekaran [42] proposed another measure namely grouping efficacy 
to overcome the weaker discriminating power of grouping efficiency measure by assigning equal weight for the number of voids and the number of exceptional elements. This measure is defined as follows.
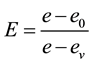
where![]()
: Total number of 1s in the matrix.
![]()
: The number of exceptional elements.
![]()
: The number of voids in the diagonal box.
![]()
Figure 1. Sample machine-component incidence matrix.
![]()
Figure 2. Rearranged machine-component matrix (block-diagonal matrix).
In this paper, these two measures are considered to measure the grouping accuracy of machine-component cell formation.
4. Fundamentals of Genetic Algorithm
Genetic algorithm (GA) applied to the machine-component cell formation problem involves the following.
・ Representation of the genes in chromosomes;
・ Selection of chromosomes for crossover;
・ Crossover and mutation operations;
・ Repair strategy.
In the GA algorithm proposed in this paper, an initial population is generated randomly and the fitness function value of each of the chromosomes is then evaluated. Then, the processes of crossover and mutation are applied over the chromosomes of a subpopulation to produce their offspring. Then their fitness function values are evaluated. Then these offsprings replace the corresponding chromosomes in the population. This process is repeated for a specified number of iterations (generations) and finally the best fitness function value among the machine-component cell formations with respect to the top most machine chromosome and component chromosome of all the generations is selected as the final solution and the corresponding machine-component cell formation result is suggested for implementation.
4.1. Representation and Selection of Chromosomes
In this paper, each chromosome is represented based on the representation followed by Venugopal and Narendran’s [27] . The chromosomes are classified into two types, viz. machine chromosomes and component chromosomes.
Gene positions from left to right in a machine chromosome represent the machine numbers from low to high, respectively. The number of genes in a machine chromosome is equal to the number of machines. The gene value at a particular gene position of a machine chromosome represents the cell number to which the corresponding machine is assigned.
Similarly, gene positions from left to right in a component chromosome represent the component numbers from low to high, respectively. The number of genes in a component chromosome is equal to the number of components. The gene value at a particular gene position of a component chromosome represents the cell number to which the corresponding component is assigned.
4.2. Two-Point Crossover Method
The genetic algorithm uses two-point crossover method for machine chromosomes as well as component chromosomes. Consider two machine chromosomes as shown in Figure 3. The chromosomes consist of eight genes. The number of machine cells 4. So, the gene values in both the chromosomes are in between 1 and 4, both inclusive.
Now, randomly generate two crossover points and let them be 3 and 6. The offsprings based on the two-point crossover method are shown in Figure 4.
In Figure 4, the machine offspring 1 is obtained by copying the genes at gene positions 1 and 2 of the machine chromosome 1 and the genes at the gene positions 3, 4, 5 and 6 of the machine chromosome 2 and the genes at the gene positions 7 and 8 of the machine chromosome 1. Similarly, the machine offspring 2 is obtained by copying the genes at the gene positions 1 and 2 of the machine chromosome 2, genes at the gene positions 3, 4, 5 and 6 of the machine chromosome 1 and the genes at the gene positions 7 and 8 of the machine chromosome 2.
The consecutive pairs of machine chromosomes are taken at a time and then the two-point crossover method is applied on them to obtain their corresponding offspring. The method is also used for the component chromosomes.
4.3. Mutation
Mutation is the process of randomizing the genes by swapping the genes at two randomly selected positions of each offspring obtained after crossover of two chromosomes. This is done based on a given probability for mutation. If the generated probability is less than or equal, say 0.30, then mutation will be performed; otherwise, the mutation will be not performed on the offspring.
4.4. Repair Strategy for Offspring
The offspring obtained after the crossover and mutation operations may be infeasible or ill-structured. Under such situation, a new repair strategy is applied to obtain a feasible offspring.
Let a sample new machine offspring after the crossover and mutation operations be as shown below.
New machine offspring: 2 4 1 4 1 2
In the machine offspring, the machine cell numbers are 1, 2 and 4. In this distribution of machine cell numbers, the machine cell 3 is missing, which makes the machine offspring infeasible. Hence, the cell numbers must be modified such that they are in continuous order starting from 1.
Start from left of the offspring and make the first gene to 1 and then wherever the gene value is equal to the gene value in the first position of the offspring, make it to 1.
Then move to next non-updated gene location (L) and make it to 2 and then wherever the non-updated gene value is equal to the gene value at the gene location L, make it to 2. Continue this process, until all the gene values are updated.
The resultant repaired offspring is as shown below.
Repaired offspring: 1 2 3 2 3 1
Similarly logic can be applied to repair any component offspring, if there is discontinuity in component cell numbers.
4.5. Density Index of Matching Machine Groups with Component Families
While applying the genetic algorithm to the machine-component cell formation problem, after forming machine cells and component families, next these must be matched based on certain measure. In existing researches, there is no specific method to perform this step.
In this paper, the machine cells and component families are matched based on a measure called “density index”. The computation of the density index by assigning the machine group i to the component family j is explained using some sample result shown in Figure 5.
Actually, in Figure 5, the machine cells are appropriately matched with the component families to give a sample block diagonal form. The fitness value is then calculated for this block diagonal matrix. The grouping efficiency and the grouping efficacy of this machine-component cell formation are 61.90% and 34.28%, respectively. The summary of machine-component cells is given in Table 1.
Each machine cell can be assigned to each component cell. As an example if the machine cell 1 (MC1), which consists of machines m1 and m6 is assigned to the component cell 1 (CC1), which consists of components c1 and c5, then the corresponding density index D11 is computed using the following formula. This value and other values of the density matrix are shown in Figure 6.
![]()
After applying Hungerian method designed for the assignment problem, which is proposed in this paper to match the machine groups with component families, the grouping of machine cells and component families are changed. The new block diagonal form is obtained and shown in Figure 7. The grouping efficiency and grouping efficacy of this machine-component cell formation are 70.67% and 45.45%, respectively, which are improved from the respective previous values.
5. Hybrid Genetic Algorithm
In this section, a hybrid genetic algorithm (HGA) is presented to form machine-component cells for a given cellular manufacturing system.
![]()
Table 1. Summary of machine component cells of Figure 5.
The steps of the algorithm are presented below.
Step 1: Input the following.
・ Number of machines![]()
;
・ Number of components![]()
;
・ Machine component incidence matrix![]()
;
・ Size of the population of machine chromosomes (N1) as well as component chromosomes (N1) ;
・ Set generation count (GC) = 1.
・ Maximum number of generations to be carried out (MNG)
Step 2: Find the integer values of m/2 and n/2 rounded to next integer and find the minimum of them.Treat it as the maximum number of cells (MC).
Step 3: Generate an initial population of machine chromosomes by assigning the machines to different cells in the range from 1 to MC. A sample machine chromosome is shown in Table 2 by assuming MC as 2.
Step 4: For each of the machine chromosomes, find ideal seed for machine chromosome as well as for component chromosome by performing the following.
4.1) Form machine groups. The machine groups of the machine chromosome shown in Table 2 are given in Table 3.
4.2) Form component groups based on the machine groups by following the guidelines given below.
・ Assign a component to a machine cell in which it has the maximum number of operations;
・ In case of tie on the maximum number of operations, break the tie randomly.
Let the number of component groups be CG.
4.3) If the number of machine groups is equal to the number of component families, find the desired measure of performance: Grouping efficiency (or) Grouping efficacy and go to Step 5;
Otherwise, go to Step 4.4.
4.4) Form machine groups based on the component groups obtained in Step 4.2 by following the guidelines given below.
・ Assign a machine to a component cell in which it processes maximum number of components;
・ In case of tie on the maximum number of components processed by the machine, break the tie randomly.
Let the number of machine groups be MG.
4.5) If the number of machine groups is equal to the number of component groups, find the desired measure of performance: Grouping efficiency (or) Grouping efficacy and go to Step 5; Otherwise, go to Step 4.2.
Step 5: Sort the machine groups and component groups together in the decreasing order of their fitness function values, either grouping efficiency or grouping efficacy as the case may be.
Step 6: Select the top most 30% of the sorted population rounded to an even number and let the size of this subpopulation be N2.
Step 7: For each of the successive two machine chromosomes as well as for each of the successive two component chromosomes, perform the following.
7.1) Perform two-point crossover operation to obtain their corresponding two offspring.
7.2) Perform mutation with a mutation probability of 0.30 on each of the machine offsprings as well as component offsprings.
7.3) If some of the machine cell numbers are missing in a machine offspring, repair the respective machine offspring, which will modify the machine cell numbers so that they are continuous from the machine cell number 1 onwards.
![]()
Table 2. Sample machine chromosome.
![]()
Table 3. Machine groups of machine chromosome.
7.4) If some of the component facility numbers are missing in a component offspring, repair the respective component offspring, which will modify the component family numbers so that they are continuous from the component family number 1 onwards.
7.5) Perform further repair on either machine offspring or component offspring to bring equality in the number of machine cells and the number of component families.
7.6) For each of the machine offspring and component offspring combination, perform the following.
7.6.1) Form density matrix![]()
, which represents density of 1s in the sub matrix in the machine-component incidence matrix with respect to the ![]()
machine cell and the ![]()
component family, for ![]()
and![]()
.
7.6.2) Using Hungarian method which is designed for assignment problem, match the machine groups with the component families such that the resultant sum of the density values is maximized to obtain a machine- component cell formation.
7.6.3) Find the fitness function value (grouping efficiency or grouping efficacy) for the machine-component cell formation obtained in Step 7.6.2.
Step 8: Store the machine offspring and component offspring of the subpopulation in the respective chromosomes of the population.
Step 9: Sort the machine chromosomes and component chromosomes together in the decreasing order of their fitness function values, either grouping efficiency or grouping efficacy as the case may be.
Step 10: Increment the generation count by 1 (GC = GC + 1).
Step 11: If GC ≤ MNG then go to Step 6.
Step 12: Rework the results of the topmost machine chromosome and component chromosome by following the step 7.6 and print the corresponding machine-component cell formation and the grouping efficiency or grouping efficacy.
6. Comparison of HGA with Existing Algorithms
The performance of the hybrid genetic algorithm (HGA) presented in this research is compared with four other existing algorithms, viz. ZODIAC (Chandrasekharan and Rajagopalan [43] ), GRAFICS (Srinivasan and Narendran [20] ), Algorithm-1 (Nambirajan and Panneerselvam [44] ) and Algortihm-2 (Nambirajan and Panneerselvam [24] ). The HGA algorithm is coded in C++ and all experiments are executed on personal computer with i5 processor in Window-7 operating system.
A complete factorial experiment is designed to examine the effects of two factors, viz. “Problem Size” and “Algorithm” and their interaction on grouping efficiency as well as groping efficacy.
The number of levels of the factor “Problem Size” is 14 and they are in terms of “Number of machines” and “Number of components” are 5 × 7, 7 × 7, 8 × 20, 9 × 10, 10 × 12, 12 × 19, 14 × 24, 15 × 10, 20 × 20, 20 × 40, 24 × 40, 30 × 50, 40 × 20 and 40 × 40. The number of levels of the factor “Algorithm” is 5 (Proposed algorithm and four existing algorithms). The number of replications carried out under each of the experimental combinations is 2. So, the total number of observations of this experiment is 140 (14 × 5 × 2) for each of the grouping measures. The data for all the replications under each experimental combination are selected from literature, which are as cited in Table 4 for grouping efficiency as well as in Table 5 for grouping efficacy.
The model of ANOVA is as given below.
![]()
where ![]()
is the ![]()
replication under the ![]()
treatment of the Factor A and the ![]()
treatment of the
Factor B.
![]()
is the overall mean of the response.
![]()
is the effect of the ![]()
treatment of the Factor A on the response.
![]()
is the effect of the ![]()
treatment of the Factor B on the response.
![]()
is the interaction effect of the ![]()
treatment of the Factor A and the ![]()
treatment of the Factor B on the response.
![]()
is the random error associated with the ![]()
replication under the ![]()
treatment of the Factor A and the ![]()
treatment of the Factor B.
![]()
Table 4. Results of grouping efficiency.
![]()
Table 5. Results of grouping efficacy.
In this model, the Factor ![]()
(Problem size) is a random factor and the Factor ![]()
(Algorithm) is a fixed factor. Since, the Factor A is a random factor, the interaction ![]()
is also a random factor. The replications are always random and the number of replication under each experimental combination is k. The derivation of the expected mean square (EMS) formulas for this combination of factors is given in Panneerselvam [59] . To test the effect of ![]()
as well as![]()
, the respective F ratio is formed by dividing the mean sum of squares of the respective component (![]()
or![]()
) by the mean sum of squares of error. The F ratio for the component ![]()
is formed by dividing its mean sum of squares by the mean sum of squares of![]()
.
The alternative hypotheses of this model are as stated below.
H1: There is a significant difference between the different pairs of treatments of the Factor A (Problem Size) in terms of grouping efficiency/grouping efficacy.
H2: There is a significant difference between the different pairs of treatments of the Factor B (Algorithm) in terms of grouping efficiency/grouping efficacy.
H3: There is a significant difference between the different pairs of interaction between Factor A and Factor B in terms of grouping efficiency/grouping efficacy.
6.1. Comparison of Algorithms Based on Grouping Efficiency
This section presents the comparison of algorithms based on grouping efficiency. The ANOVA results of the grouping efficiency measure shown in Table 4 are shown in Table 6.
From the results shown in the Table 6, it is clear that the factor “Problem Size” and the factor “Algorithm” are having significant effect on the grouping efficiency.
Since there is significant difference between the algorithms in terms of grouping efficiency, next the best algorithm is obtained using Duncan’s multiple range test.
The treatment means in terms of grouping efficiency with respect to the algorithm are shown in Figure 8 in ascending order from left to right. The standard error is obtained using the following formula. One can notice the fact that the mean sum of squares of the interaction term AB is used in estimating the standard error, because the F ratio for the factor ‘Algorithm” is obtained by dividing its mean sum of squares by the mean sum of squares of the interaction ![]()
(Panneerselvam [59] ).
![]()
By referring to Duncan’s table (Panneerselvam [59] ), at a significant level of 0.05, the Least Significant Range (LSR) for each of the pairs of treatments of the Factor B is computed and shown in Figure 8 along with the actual difference between the means of that pair of treatments. From Figure 8, it is clear that the proposed HGA is significantly different from all other algorithms and it is superior to all of them in terms of grouping efficiency.
6.2. Comparison of Algorithms Based on Grouping Efficacy
This section presents the comparison of algorithms based on grouping efficacy. The ANOVA results of the grouping efficiency measure shown in Table 5 are shown in Table 7.
From the results shown in the Table 7, it is clear that the factor “Problem Size” and the factor “Algorithm” are having significant effect on the grouping efficacy.
![]()
Table 6. ANOVA results of grouping efficiency measure.
![]()
Table 7. ANOVA results of grouping efficacy.
![]()
Figure 8. Duncan’s multiple range tests for grouping efficiency.
![]()
Figure 9. Duncan’s multiple range tests for grouping efficacy.
Since there is significant difference between the algorithms in terms of grouping efficacy, next the best algorithm is obtained using Duncan’s multiple range test.
The treatment means in terms of grouping efficacy with respect to the algorithm are shown in Figure 9 in ascending order from left to right. The standard error for this performance measure is 1.1177.
By referring to Duncan’s table (Panneerselvam [59] ), at a significant level of 0.05, the Least Significant Range (LSR) for each of the pairs of treatments of the Factor B is computed and shown in Figure 9 along with the actual difference between the means of the grouping efficacy of that pair of treatments. From Figure 9, it is clear that the proposed HGA is significantly different from all other algorithms and it is superior to all of them in terms of grouping efficacy.
7. Conclusion
The cellular manufacturing system helps companies to improve productivity by way of combining the benefits of process layout and product layout. In this paper, the design of machine-component cells for a given machine- component incidence matrix is attempted. Since this problem is a combinatorial problem, a hybrid genetic algorithm is developed to maximize each of the performance measures, viz. grouping efficiency and grouping efficacy. Then, it is compared with four existing algorithms for each of the performance measures using a complete factorial experiment, in which the problem is treated as one factor and the algorithm is treated as another factor. It is found that the proposed hybrid genetic algorithm surpasses the performances of all other four algorithms. The construction of machine chromosomes and component chromosomes, and also the use of Hungerian method to match the machine groups with component families are unique contribution of this research.
Acknowledgements
The authors sincerely thank anonymous referees for their constructive suggestions, which help to improve the paper.