Precessing Ball Solitons as Self-Organizing Systems during a Phase Transition in a Ferromagnet ()
1. Introduction
It is known that a very large number of phenomena and processes which exist in nature can be reproduced artificially, and can be classified as “self-organizing systems” or “dissipative structures” [1-4]. Even life itself in all its forms is an example of such a structure. Processes belonging to this category, which can be demonstrated on a laboratory table are, for example, the chemical “Zhabotinskiy reaction” [5,6] and “Benar effect” [7]. Some of them are periodic structures in space or time. Others are more complex. But the common feature of all these processes is that the loss of energy of the system associated with the dissipation is fully offset by the influx of energy from external sources, i.e., inflow of entropy due to the dissipation equal to the negative flow of entropy due to the coupling to an external source.
Another case of “self-organized systems”, occurring away from the equilibrium state of the system is presented in this paper.
Kinetics of the phase transition in a uni-axis ferromagnet under the action of a magnetic field along the easy axis has been considered in [8]. In such cases, in the metastable state of the crystal, precessing magnetic solitons (PBS) with the symmetry of the ellipsoid can spontaneously arise. The precession frequency and, correspondingly, the amplitude, size and energy of PBS are characterized by a continuous spectrum. The PBS can grow and transform into the macroscopic domain of a new phase state. This transformation is related to the energy dissipation and, as a result of this process, the PBS quickly disappear.
In the present paper we consider the conditions when, in addition to the main magnetic field that provides phase transition, a periodic magnetic field perpendicular to the easy axis operates. In such a case, only solitons with the precession frequency equal to the frequency of the magnetic field could arise. In this case, there is a stabilization of PBS, i.e. a “freeze” of them, and, most importantly, fully compensation of changes in entropy, and thus above conditions for the existence of “self-organizing systems” are fulfilled.
The next chapter is a theoretical introduction to the physics of precessing magnetic solitons in phase transition with the additional action of a periodic magnetic field. The last chapter presents several examples of equilibrium PBS, which are “self-organizing systems”, showing their main characteristics and the conditions of their occurrence.
2. Equations for PBS
In the given article, to analyze magnetic solitons in a ferromagnet at the first-order transition in the presence of periodic magnetic field, as in [8], we use the LandauLifshitz equation [9] with a Gilbert form of dissipative term:
 (1)
(1)
and corresponding expression for the density of thermodynamic potential (as in [8])
 (2)
(2)
Here ,
,  is the periodic field directed perpendicular to the Z-axis,
is the periodic field directed perpendicular to the Z-axis,  ,
, ; m is a non-dimensional vector of ferromagnetism equal in the absolute value to 1;
; m is a non-dimensional vector of ferromagnetism equal in the absolute value to 1; , in initial state:
, in initial state: .
.
Further, we consider the PBS in a flat plate perpendicular to the Z-axis, use the following dimensionless values:
 ,
,  ,
,
 ,
,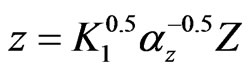 ;
;
and note:
 ,
,
 .
.
If the added periodic field is
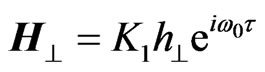 (3)
(3)
and to present the expression for magnetic component in the view
 (4)
(4)
(here we restrict ourselves to the case of moveless solitons, but the phase of precession of magnetic moments differs from the phase of periodic field and depends on a radius, i.e. ), we obtain the following equations for
), we obtain the following equations for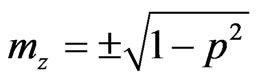 :
:
 (5)
(5)
 (6)
(6)
From (5), we obtain the expressions for the density of PBS energy relative to the initial state, together with the energy of interaction with the external field (see, for example [8]):
 (7)
(7)
and for the change of this energy connected with dissipation and the action of the external periodic field:
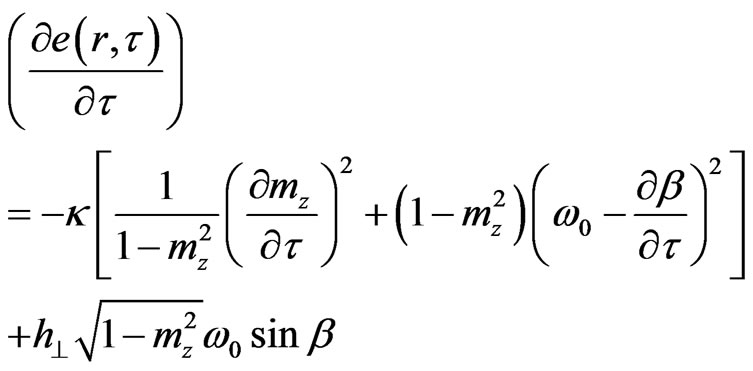 (8)
(8)
The Equations (5)-(8) constitute a complete description of PBS, including their time transformation. However, in the given paper we consider only the equilibrium state of PBS inside the ferromagnet, i.e. when the decrease of energy caused by dissipation is compensated by energy flow from the external periodic field, i.e. . Furthermore, in this case,
. Furthermore, in this case,  ,
, . Therefore, for the equilibrium state of PBS we have the following expressions:
. Therefore, for the equilibrium state of PBS we have the following expressions:
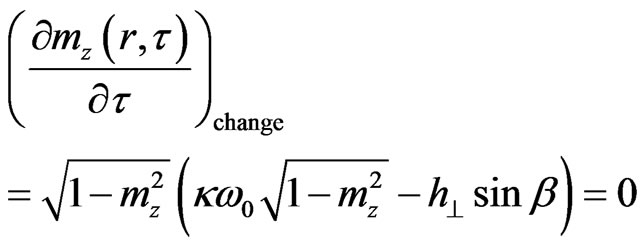 (9)
(9)
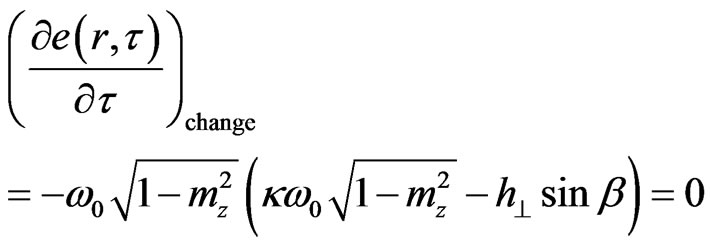 (10)
(10)
and the relation:
 , (11)
, (11)
where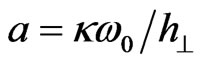 .
.
Correspondingly, the equation for equilibrium PBS is the following:
 (12)
(12)
In our case, equilibrium PBS are “self-organizing systems” or “dissipative structures” [1-3] that can arise spontaneously in a metastable state during the first-order phase transition to the stable equilibrium state, i.e. to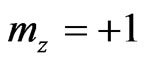 . For such PBS—the dissipative structures, the entropy increase connected with dissipation is compensated by the decrease of the entropy that due the external periodic field. It can be expressed as follows:
. For such PBS—the dissipative structures, the entropy increase connected with dissipation is compensated by the decrease of the entropy that due the external periodic field. It can be expressed as follows:
 , (13)
, (13)
where
 . (14)
. (14)
3. Characteristics of Equilibrium PBS
It follows from the foregoing that at the action of a periodic magnetic field only the PBS with a frequency specified by this field may arise spontaneously. This is different from the phase transition discussed in [8], where the frequency and, accordingly, the configuration of arising PBS are not defined.
In Figures 1-3, the configurations of the PBS for several frequencies of precession at ,
,  are presented. For each frequency, there is the solution of the Equation (12) with corresponding PBS that precesses in substratum of uniform precession of the bulk crystal. Beside such solution, there is the solution that corresponds to homogeneous precession of magnetic moments, without soliton. Such a solution at
are presented. For each frequency, there is the solution of the Equation (12) with corresponding PBS that precesses in substratum of uniform precession of the bulk crystal. Beside such solution, there is the solution that corresponds to homogeneous precession of magnetic moments, without soliton. Such a solution at  is shown in Figure 1.
is shown in Figure 1.
Note that the maximum frequency of PBS at  without periodic field equals
without periodic field equals  and corresponds to magnetic resonance in a metastable state. In Figure 1 and in the following examples, the same parameters as in the [8] article
and corresponds to magnetic resonance in a metastable state. In Figure 1 and in the following examples, the same parameters as in the [8] article
( ,
, ,
,
 ) are used and furthermore,
) are used and furthermore, 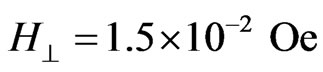 ,
, .
.
In Figures 4 and 5, the frequency dependencies for main parameters of PBS at  are presented:
are presented:
the energy  (in correspondence with (7)); the amplitude
(in correspondence with (7)); the amplitude 
(here 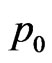 is the amplitude of uniform precession); and radius of PBS is
is the amplitude of uniform precession); and radius of PBS is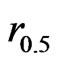 .
.
As can be seen from (11), if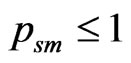 , the equilibrium state of PBS is possible only under the condition:
, the equilibrium state of PBS is possible only under the condition:
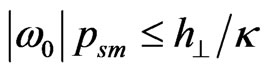 . (15)
. (15)
Frequency range of equilibrium PBS increases with the increase of periodic field amplitude. For , if
, if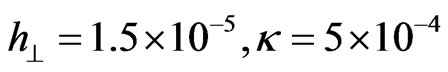 , condition
, condition  corresponds to
corresponds to . If
. If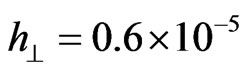 , then
, then  (see in Figures 4 and 5).
(see in Figures 4 and 5).
The possibility of equilibrium PBS is connected with the fact, that during their precession, the magnetic moments lag by phase behind precession of periodic field. In the Figures 6 and 7, the frequency dependency of the

Figure 7. The same frequency dependency if the  angle as in Figure 6 in the range near
angle as in Figure 6 in the range near .
.
angle of such a delay in center of PBS, i.e. , is shown. Besides, in Figure 6 the curve of corresponding exponential factor, that defines temperature dependency of the PBS probability, is presented. The probability of PBS origin decreases sharply at the increase of PBS energy.
, is shown. Besides, in Figure 6 the curve of corresponding exponential factor, that defines temperature dependency of the PBS probability, is presented. The probability of PBS origin decreases sharply at the increase of PBS energy.
If the magnetic field  is enough large, the equilibrium PBS with amplitude
is enough large, the equilibrium PBS with amplitude  are possible. It is obviously in such cases, the condition for equilibrium PBS can be written as:
are possible. It is obviously in such cases, the condition for equilibrium PBS can be written as:
 . (16)
. (16)
In Figures 8 and 9, two examples of such case for  are presented. As seen in the second example, in Figure 9, the equilibrium PBS are possible with the negative energy and at
are presented. As seen in the second example, in Figure 9, the equilibrium PBS are possible with the negative energy and at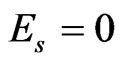 , i.e. in the bifurcation point b. The configuration of such equilibrium PBS is shown in Figure 10.
, i.e. in the bifurcation point b. The configuration of such equilibrium PBS is shown in Figure 10.
The probability of the equilibrium PBS near the bifurcation point where  increases sharply is shown in Figure 11. The energy 25 meV corresponds to temperature about 290 K.
increases sharply is shown in Figure 11. The energy 25 meV corresponds to temperature about 290 K.
4. Conclusions
Periodic magnetic field acting perpendicular to the axis of easy magnetization, i.e. perpendicular to the main magnetic field, leads to a significant change in the nature of the precessing magnetic solitons in the first order transition, in comparison with [8].
1) Near the boundary of the existence of the metastable state, only PBS with precession frequency equals

Figure 11. Frequency dependencies of the energy, β angle in center of PBS (noted by asterisks) and exponential temperature factor for equilibrium PBS at ,
, . The bifurcation point is noted as b.
. The bifurcation point is noted as b.
the frequency of the external field can occur. The frequency of the external field specifies uniquely of other characteristics of PBS (amplitude, configuration, energy) too.
2) Arising PBS are equilibrium, i.e. reducing their energy due to dissipative processes is fully compensated by the influx of energy from an external periodic field.
3) We can consider the equilibrium PBS as “dissipative structures” or “self-organizing systems” [1-3], when the increase of entropy connected with energy dissipation is compensated by a negative flow of entropy due to the action of an external periodic field.
4) At the phase transition in a ferromagnet, the dissipative structures in the form of equilibrium PBS can be originated not only in the presence of the bifurcation point, but also in a more general case: when the energy of PBS state is small enough.
5) The compensation of energy and entropy is accompanied by the fact that PBS during the precession are delayed by phase behind the precession of a periodic field. The magnitude of this delay depends on the radius and the maximum delay is at the center of PBS.
6) On the side of the positive values of frequencies, amplitude and frequency of precession of equilibrium PBS are defined by the following relations:

and  if
if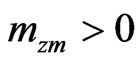 .
.