Generation of Non-Gaussian Wide-Sense Stationary Random Processes with Desired PSDs and PDFs ()
1. Introduction
Generating and representing of a Gaussian variable with desired PSD is an easy job. A usual method is to use simple linear time invariant filter with a Gaussian random variable as an input. The problem of generating correlated non-Gaussian random series has been of great interest during the last three decades in connection with the simulation of processes in communication systems such as radar, sonar and speech. Furthermore, it can be applicable in recent military approaches. Groups of stealth aircrafts generate random noise with  distribution to be hidden under clutter noise from active radars. The generation of non-Gaussian signals has given rise to a renewed interest in the mechanical vibration fields and defense industries for some reasons. The realization of many surface transportation and wave environments are non-Gaussian, also the development of shaker control systems that can replicate long time histories are non-Gaussian. Many original current shaker control systems, for generating random vibration tests generate only Gaussian random noise. However, waveform replication techniques now allow the reproduction of any waveforms whose characteristics are within the bounds of a shaker [1,2]. Most of the approaches suggested involve the non-linear transformation of colored Gaussian random series or use linear transformation of non-Gaussian no correlated time series. All these methods require a complicated optimization procedure to achieve the desired properties [3,4]. The zero memory non-linear ZMNL in [3] is chosen so that the desired distribution is exactly realized and the digital filter is designed so that the specific auto-covariance is closely approximated. In this method, the autocorrelation of sequence at the output of the filter may be negative hence the method can fail because in this case we should calculate several hundreds or even thousands of unknowns, on the other hand ergodicity has not been mentioned in this paper. In addition, the method is too complex to be implemented but it can be helpful in this paper for first approximation with some promotion. In [5], a correlated Gaussian random process is multiplied by a modulating sequence. The main problem is in determining the modulating sequence, which can be difficult if not impossible. Furthermore, the generated sequence is not ergodic. In [6], a nonlinearity is used and due to the nonlinearities in these schemes, it seems that the results cannot be extended to the general cases such as multidimensional and multichannel random processes. The method suggested in [7], is based on [3] and decreases some problems and produces wide-sense stationary and ergodic sequences asymptotically or as the number of generated data goes to infinity. In [8] proposed a method that decouples the problem into two separate ones for some signal characteristics such as even and infinitely divisible first-order PDF, but it can generate every continuous PSDs. The method can be limited because the Hankel transform of every PDFs cannot be calculated easily. The restriction of an even PDF limits us to generate vast major PDFs such as Rayleigh, Nakagami, flicker and square Gaussian noises. The assumption of an infinitely divisible PDF may be restrictive too. However, the strategy mentioned in [8] is a constructive tool to be used under some modifications. In this paper, we divide desired PDF with a number of symmetric and infinitely divisible ones that these PDFs depend on the first estimation. In contradiction to [8] there is not any restriction on the PDF. This paper consists of five section, in section 2 a basic function which has been derived from [8] is considered and extended to more general form and the nonlinear transform function is described for closed form first approximation. In section 3, with some assumption we prove that this function has ergodicity properties in both means and variances and the way to compute a nonlinear transform function has been described. In section 4, a complex signal with asymmetric PDF and desired PSD are generated. The conclusion has been given in section 5.
distribution to be hidden under clutter noise from active radars. The generation of non-Gaussian signals has given rise to a renewed interest in the mechanical vibration fields and defense industries for some reasons. The realization of many surface transportation and wave environments are non-Gaussian, also the development of shaker control systems that can replicate long time histories are non-Gaussian. Many original current shaker control systems, for generating random vibration tests generate only Gaussian random noise. However, waveform replication techniques now allow the reproduction of any waveforms whose characteristics are within the bounds of a shaker [1,2]. Most of the approaches suggested involve the non-linear transformation of colored Gaussian random series or use linear transformation of non-Gaussian no correlated time series. All these methods require a complicated optimization procedure to achieve the desired properties [3,4]. The zero memory non-linear ZMNL in [3] is chosen so that the desired distribution is exactly realized and the digital filter is designed so that the specific auto-covariance is closely approximated. In this method, the autocorrelation of sequence at the output of the filter may be negative hence the method can fail because in this case we should calculate several hundreds or even thousands of unknowns, on the other hand ergodicity has not been mentioned in this paper. In addition, the method is too complex to be implemented but it can be helpful in this paper for first approximation with some promotion. In [5], a correlated Gaussian random process is multiplied by a modulating sequence. The main problem is in determining the modulating sequence, which can be difficult if not impossible. Furthermore, the generated sequence is not ergodic. In [6], a nonlinearity is used and due to the nonlinearities in these schemes, it seems that the results cannot be extended to the general cases such as multidimensional and multichannel random processes. The method suggested in [7], is based on [3] and decreases some problems and produces wide-sense stationary and ergodic sequences asymptotically or as the number of generated data goes to infinity. In [8] proposed a method that decouples the problem into two separate ones for some signal characteristics such as even and infinitely divisible first-order PDF, but it can generate every continuous PSDs. The method can be limited because the Hankel transform of every PDFs cannot be calculated easily. The restriction of an even PDF limits us to generate vast major PDFs such as Rayleigh, Nakagami, flicker and square Gaussian noises. The assumption of an infinitely divisible PDF may be restrictive too. However, the strategy mentioned in [8] is a constructive tool to be used under some modifications. In this paper, we divide desired PDF with a number of symmetric and infinitely divisible ones that these PDFs depend on the first estimation. In contradiction to [8] there is not any restriction on the PDF. This paper consists of five section, in section 2 a basic function which has been derived from [8] is considered and extended to more general form and the nonlinear transform function is described for closed form first approximation. In section 3, with some assumption we prove that this function has ergodicity properties in both means and variances and the way to compute a nonlinear transform function has been described. In section 4, a complex signal with asymmetric PDF and desired PSD are generated. The conclusion has been given in section 5.
2. Definition and Properties
We propose a new method to generate arbitrary continuous PSDs and first-order PDFs. In this method, one can generate a discrete signal by dividing the desired PDF into a number of symmetric PDFs. In general form we define  for
for  as follows
as follows
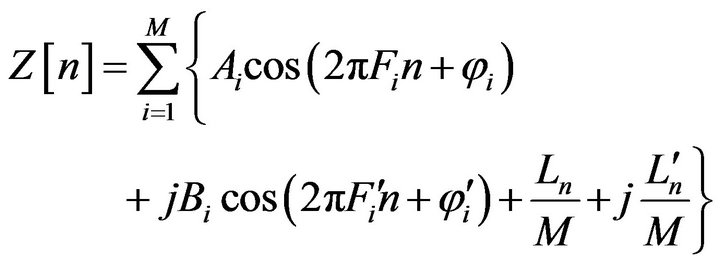 (1)
(1)
 (2)
(2)
where 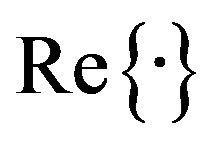 and show real and imaginary parts of
and show real and imaginary parts of  respectively that are independent from each other. In (1)
respectively that are independent from each other. In (1) ,
,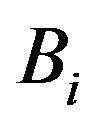 ,
,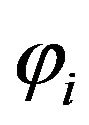 ,
, ,
, and
and 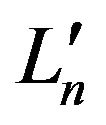 are random variables with the following definitions
are random variables with the following definitions
 (3)
(3)
 (4)
(4)
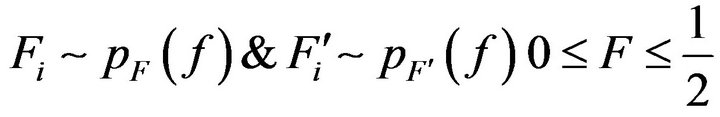 (5)
(5)
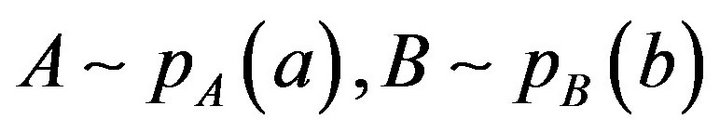 (6)
(6)
In all sections of this article, we assume  and
and  each have equal distributions. By considering the above-mentioned relations the following are shown in appendix 1) The mean of
each have equal distributions. By considering the above-mentioned relations the following are shown in appendix 1) The mean of  is
is
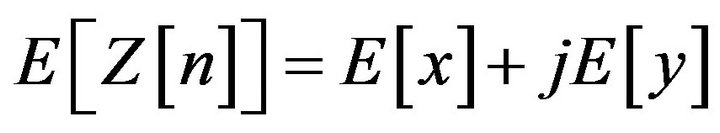 (7)
(7)
The mean of every PDFs is a deterministic value and it forces the PSD to have a  function in zero. Therefore, it can be subtracted from
function in zero. Therefore, it can be subtracted from .
.
1) The random process is the wide sense stationary with the following autocorrelation function
 (8)
(8)
where 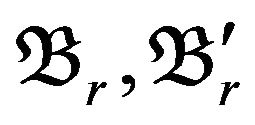 are
are  respectively. Actually, the power spectral density is equal to
respectively. Actually, the power spectral density is equal to
 (9)
(9)
Now we can use the nonlinear transform function in order to achieve the first approximation of the desired spectrum and the first order statistical probability density function. This spectrum can be converged exactly on desired one by using  and
and
 terms, with negligible deviation from main PDF. Because of positive definition of
terms, with negligible deviation from main PDF. Because of positive definition of  and
and 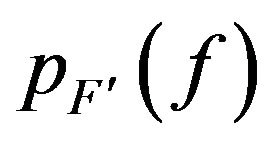 we should have
we should have
 (10)
(10)
where 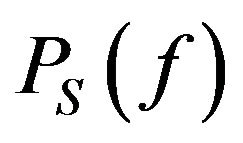 is the desired power spectrum.
is the desired power spectrum.
3) The PDF of  and
and  can be written as
can be written as
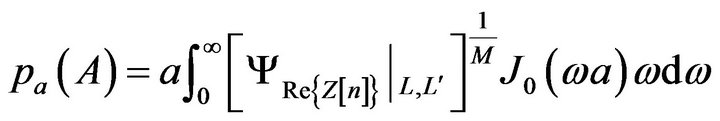 (11)
(11)
 (12)
(12)
where 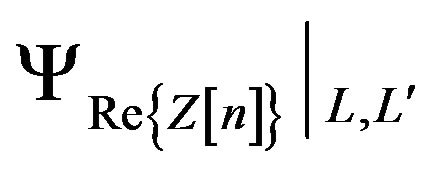 and
and  are the two characteristic functions for symmetric PDFs with proper variance and zero mean, for a Gaussian
are the two characteristic functions for symmetric PDFs with proper variance and zero mean, for a Gaussian  we have
we have

therefore
 (13)
(13)
and we can solve the above relation by using Hankel transformation of , hence
, hence
 (14)
(14)
similarly, we have
 (15)
(15)
In order to use the nonlinear transform function, consider the following relation between two random variables of  and
and 
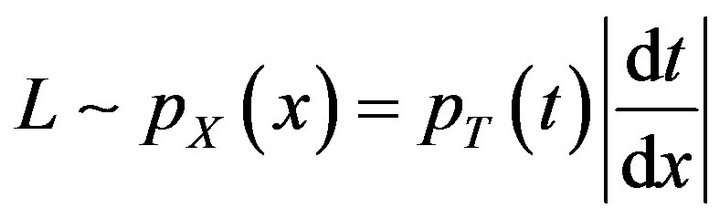 (16)
(16)
where 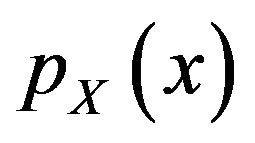 and
and  are probability density functions for
are probability density functions for  and
and  random variables respectively. Similarly, for both random variables of
random variables respectively. Similarly, for both random variables of  and
and  we have
we have
 (17)
(17)
It is understood that in Equations (16) and (17),  stands for
stands for  and
and , the
, the  and
and  are the density functions which are dependent on
are the density functions which are dependent on  and
and  variables. In this paper all the relations and calculations on
variables. In this paper all the relations and calculations on ,
,  variables can be modified to
variables can be modified to ,
,  variables.
variables.
If  is not monotonically increasing, the function must be broken into parts, and each part is handled separately. For the purposes of this article
is not monotonically increasing, the function must be broken into parts, and each part is handled separately. For the purposes of this article  will be restricted to its derivation function. Therefore, the sign of
will be restricted to its derivation function. Therefore, the sign of can be negative or positive. The conversion of a realization of
can be negative or positive. The conversion of a realization of  to
to  using a nonlinear function will always produce a PSD for
using a nonlinear function will always produce a PSD for  that is different from the PSD of
that is different from the PSD of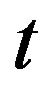 . The effect is to add harmonics to all the Fourier components of
. The effect is to add harmonics to all the Fourier components of . This will make the transformed data appear “whiter” than the original data [9,10]. However, most of the spectral information is contained in the zero crossings which are preserved, and if the nonlinearity is not too great, the spectral change is usually acceptable and the PSD of
. This will make the transformed data appear “whiter” than the original data [9,10]. However, most of the spectral information is contained in the zero crossings which are preserved, and if the nonlinearity is not too great, the spectral change is usually acceptable and the PSD of  will be near the PSD of
will be near the PSD of . The practical utility of these results is that the PSD may be approximated from (9) by using nonlinear transform function on
. The practical utility of these results is that the PSD may be approximated from (9) by using nonlinear transform function on 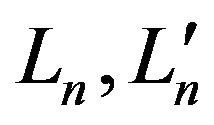 and is converged to exact form by choosing the PDF of frequencies
and is converged to exact form by choosing the PDF of frequencies  and
and  properly.
properly.
3. Ergodicity Properties, Nonlinear Function Synthesizing
The main problem in applications of stochastic processes is the estimation of various statistical parameters in terms of real and imaginary parts. It is clear that the basic Equation (1) contains two mathematical terms, the first one is

which its ergodicity of mean and variance has been proven in [1]. The second term is , where
, where 
 and
and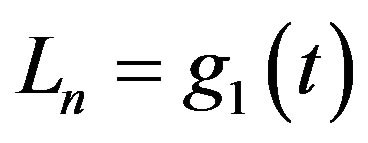 ,
,  therefore if
therefore if 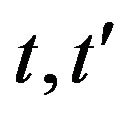 has an ergodic properties and
has an ergodic properties and 
 both
both  and
and  have ergodicity properties too. In other words, Equation1 under certain conditions has ergodicity properties. Now it is clear, that the main problem is to synthesize
have ergodicity properties too. In other words, Equation1 under certain conditions has ergodicity properties. Now it is clear, that the main problem is to synthesize  and
and  under the limitation of Equation (10). The total power spectrum can be divided as follows
under the limitation of Equation (10). The total power spectrum can be divided as follows

where  and
and  are the power spectrum of real and imaginary parts respectively. Therefore, we can assume
are the power spectrum of real and imaginary parts respectively. Therefore, we can assume
 (18)
(18)
Both strategies on imaginary and real parts are like each other. Equation (18) can be simplified as
 (19)
(19)
and
 (20)
(20)
 (21)
(21)
If  and t has a Gaussian distribution
and t has a Gaussian distribution
 (22)
(22)
Now we propose a computational method to generate a proper function of , set
, set  where we select
where we select  as large as possible, considering small positive value for
as large as possible, considering small positive value for , we have
, we have
for 
while 


if 

end

end
end
Where  is a large number which
is a large number which , Figure 1 shows nonlinear function synthesizing to generate uniform PDF in [–0.5, 0.5] interval. It is clear that generated function guarantees the Equations (20) and (21).
, Figure 1 shows nonlinear function synthesizing to generate uniform PDF in [–0.5, 0.5] interval. It is clear that generated function guarantees the Equations (20) and (21).
4. Some Examples of Generating Asymmetric and PDF with Desired PSD
4.1. One Dimensional Real Signal
Consider the representation of a WSS Rayleigh random process with the variance of , mean given by
, mean given by
 , and a given continuous PSD. To represent and generate this process we need determining a nonlinear transform function to convert Gaussian distribution of
, and a given continuous PSD. To represent and generate this process we need determining a nonlinear transform function to convert Gaussian distribution of  to Rayleigh PDF, the PDFs of the amplitude and frequency can be calculated after the first approximation of desired PSD. Figure 2 shows a nonlinear transform function to convert Gaussian with shaped spectrum to Rayleigh one. Figure 3 depicts the Rayleigh PDF, the blue curve in Figure 4 shows the first approximated power spectral density and the red dashed line shows desired spectrum. We define the following error function
to Rayleigh PDF, the PDFs of the amplitude and frequency can be calculated after the first approximation of desired PSD. Figure 2 shows a nonlinear transform function to convert Gaussian with shaped spectrum to Rayleigh one. Figure 3 depicts the Rayleigh PDF, the blue curve in Figure 4 shows the first approximated power spectral density and the red dashed line shows desired spectrum. We define the following error function
 (23)
(23)
This error function can be decreased by the use of sinusoidal terms
 (24)
(24)
where

and
 (25)
(25)
Therefore, the frequency PDF can be calculated as the following relation
 (26)
(26)
also
 (27)
(27)
The average of 10,000 realizations of a periodogram along with the true PSD (indicated by the black curve) is shown in Figure 4. It is interesting to note that the generated PDF has less accuracy than what is calculated before adding sinusoidal term and it is depicted in Figure 5. First approximation play an important role in having a more accurate results.
4.2. Two Dimensional Complex Signal
Consider the WSS complex signal  with ar-
with ar-

Figure 2. Nonlinear transform function converting non zero mean Gaussian PDF to Rayleigh random process.

Figure 3. Generated Rayleigh random process after applying g(t) on Gaussian PDF.

Figure 4. Power spectral density synthesizing.

Figure 5. First order probability density function of Z[n], red line depicts Rayleigh PDF.
bitrary power spectral density, where  and
and  are independent from each other and represent the real and complex parts of
are independent from each other and represent the real and complex parts of  respectively. Both
respectively. Both  and
and  have desired PDF and every one generates a part of total power spectrum which depends on its variance. Therefore
have desired PDF and every one generates a part of total power spectrum which depends on its variance. Therefore , where
, where  is the PDF of a complex signal and
is the PDF of a complex signal and ,
,  represent the PDF of real and imaginary parts of the signal. Figure 6 shows a joint PDF of
represent the PDF of real and imaginary parts of the signal. Figure 6 shows a joint PDF of  and
and . If we consider
. If we consider
 (28)
(28)
and
 (29)
(29)
where
 (30)
(30)
After applying the algorithm that was mentioned in Section 3 we can achieve to proper nonlinear transform function. Figure 7 shows generated PDF and Figure 8 depicts imaginary and real parts of this discrete signal. The power spectrum can be converged to its correct response by considering proper PDF for both  and
and  values as follows
values as follows
 (31)
(31)
 (32)
(32)
Therefore
 (33)
(33)
 (34)
(34)
Generated and desired power spectral density also has been shown in Figure 9.
5. Conclusion
A new method has been presented which can generate a complex WSS random process with a desired PSD and a given first-order PDF. One of the advantages of this method is that we have no limitation on PDF to be infi-

Figure 7. Generated joint PDF of Re{Z} and Im{Z}.

Figure 8. Discrete imaginary and real parts of generated signal.

Figure 9. Synthesized power spectral density.
nitely divisible or symmetric. Also with simple computational method we can calculate proper transform function to generate desired PDF from Gaussian PDF with shaped spectrum. Furthermore, this computational method guarantees generated spectrum to be under the wanted spectrum for the first approximation. The error function is reduced to zero by the means of sinusoidal component with proper frequency and amplitude PDF, but with small deviation from exact desired PDF. In other words, there is some tradeoff between exact PDF and PSD. The ergodicity in the mean and variance has been proven under certain conditions. We have avoided bottleneck calculation of Hankel transform function that [8] faces directly to it. Because of negligible deviation from exact PDF it can be used in any practical system.
Appendix
A) Mean value

and

while

similarly

therefore

B) Autocorrelation

the above relation can be simplified as


similarly

on the other hand

and

therefore

C) PDF of A and B Assume  are constant values, with this assumption
are constant values, with this assumption



if we consider

then

and

and

Therefore,  in
in  domain can be modeled as
domain can be modeled as

by considering Bessel function characteristics we have

Therefore


suddenly

similarly
