Improving the Prediction Accuracy of Soil Mapping through Geostatistics ()
1. Introduction
The soil resource inventory, i.e. a map showing distribution of soils and its properties accompanied by a soil survey report, is the end product of a soil mapping project [1]. The paper map, as a product of traditional soil mapping, appears to be increasingly irrelevant to many users and does not have a market with land managers and policy makers at different scales [2]. While the traditional role of soil survey is diminishing, the need of soil information becomes important in terms of sustainable land management. There are many policy issues which require good soil information and rapid answers, e.g. erosion, salinization, organic matter content and heavy metal pollution. The question “Do we have enough and accurate soil data to contribute to the variety of application fields emanating from increasing societal demands?” arises.
Available soil data often fails to provide answers needed to manage our environmental resources. A lot of soil information and many maps are not being used for research because they are not available in digital formats [3,4]. Widely used soil models essentially yield empirical results due to lack of good basic soil data [5]. This challenges our scientific pretensions. Updating soil inventories is one of the main fields where new technologies should facilitate data sampling and acquisition. New high quality soil data is needed to complement existing databases and to provide spatial detail required by the users.
The Geographic Information System (GIS) is an effective and worthwhile tool in the estimation of the spatial distribution of environmental variables [6,7]. Spatial prediction and surface modeling of soil properties has become a common topic in soil science research [8,9]. The spatial distribution patterns of soil properties vary greatly depending on soil types, topography, climate, vegetation and anthropogenic activities. Surface modeling is a useful tool for soil property interpolation in precision agriculture and soil management. However, the effectiveness of the application relies on the accuracy of spatial interpolation which is used to describe the spatial variability of soil properties. The accuracy of the map reflects both the suitability of the spatial intensity of the sample collection strategy as well as the method used to predict the soil test values of all ensampled locations. It is necessary to study the interpolation methods with high accuracy and improve interpolation quality for soil properties.
Interpolation can be undertaken utilizing simple mathematical models (e.g., inverse distance weighting, trend surface analysis and splines and Thiessen polygons), or more complex models (e.g., geo-statistical methods, such as kriging) [10]. The review of comparative studies of interpolation methods applied to soil properties demonstrates that the selection of method can significantly influence map accuracy. Ordianary Kriging (OK), Universal Kriging (UK), Inverse Distance Weighting (IDW) and Radial Basis Function (splines) are four ways to interpolate soil properties. Past applications of these methods have given a range of results which have not always been consistent [11]. The performance of these three estimators was studied in soil science literature, but the results are not clear-cut. Some authors found that kriging methods out performed IDW or Radial Basis Function (Splines) [12,13]. However, others showed that kriging was not better than the other two methods [14,15].
The failure to evaluate map accuracy due to the consistency between predicted and observed attribute values for any given location within the mapped region is a recurring limitation. At present there is no consensus regarding best or most robust approaches to map soil properties. It was known little about performance and accuracy of different interpolation methods applied to soil properties. The objectives of this study are to, 1) assess the feasibility of different spatial interpolation methods to predict soil properties; 2) compare the performance and accuracy of spatially continuous interpolation of soil properties maps; and 3) develop and improve soil information systems by improving the prediction accuracy of soil properties. The aim is to answer the question: Are the traditional soil maps dying or thriving?
2. Theoretical Background
The regionalized variable theory [16] has been applied successfully to soil property interpolation for nearly 30 years [17-19]. The theory provides a convenient summary of soil variability (in the form of a semi-variogram) and an interpolation technique which is termed kriging [17,20]. To accurately characterize soil properties, more samples not fewer may be required, especially when grid or other systematic soil sampling strategies are used. At least 100 samples might be needed to obtain a reliable variogram that correctly describes spatial structure [21].
Ordinary Kriging (OK), Universal Kriging (UK), IDW and splines are four methods for interpolating soil properties. UK [16] has been the commonly used method to accommodate the trend or the changing drift, as it is sometimes known, in a soil variable. UK is a combination of the standard model of multiple-linear regression and the geostatistical method of OK [22], which is also analogous to combine soil-forming factors (known as CLORPT methods) with univariate kriging using the geographical coordinates as determining the drift. IDW [13,15] and Splines [23] are also commonly used classical interpolation methods to analyze the spatial variability of soil properties. Both kriging (OK and UK) and IDW estimate values at ensampled locations based on measurements from the surrounding locations with certain weights assigned to each of the measurements [12]. The IDW interpolator assumes that each input point has a local influence that diminishes with distance [13]. IDW does not allow assumptions required for the data [24]. To predict a value for any unmeasured location, IDW will use the measured values surrounding the prediction location. Those measured values closest to the prediction location will have more influence (weight) on the predicted value than those farther away, hence the name inverse distance weighted. Although IDW is easier and quicker to implement than kriging, it does not have the statistical advantages of kriging [23]. Splines consist of polynomials, which describe pieces of a line or surface, and they are fitted together so that they join smoothly [25]. Splines produce good results with gently varying surfaces, and thus are often not appropriate when there are large changes in the surface values within a short horizontal distance [26]. A surface does not usually fit the formulation of the spline surface theoretically, which leads to considerable interpolation error [27].
3. Materials and Methods
3.1. Study Area, Samples, and Analyses
The study area (30˚37'23.26'' - 30˚37'00.78''N, 32˚16'06.38'' - 32˚15'18.44''E), covering 50 Hectare, is located in the Ismailia province, Egypt (Figure 1). The study area was covered by 146 sampling sites. The average distance between soil sampling locations is approximately 50 m. The sampling sites were designed to cover evenly the whole area and to include different soil types, and different land use types. Soil samples were air-dried and passed through a 2 mm sieve. Soil EC was measured in a 1:1 soil/water suspension with the EC meter method [28]. Soil pH was measured in a 1:2.5 soil/water suspension with the pH meter method [29]. CaCO3 was estimated by the manometer method using Collin’s calcimeter [30]. Topsoil (in the plow 0 - 30 cm) pH, EC and CaCO3 of the 146 samples was used to compare the performance of different interpolators.
3.2. Geostatistical Methods for Interpolating Soil Properties
OK, UK, IDW and Splines are four methods for interpolating soil properties. IDW interpolation explicitly implements the assumption that things that are close to one another are more alike than those that are farther apart. The optimal power value is determined by minimizing the root mean square prediction error (RMSPE).
A Geostatistical Analyst tries several different powers for IDW to identify the power that produces the minimum RMSPE. Splines methods are a series of exact interpolation techniques; that is, the surface must go through each measured sample value. When comparing Splines to the IDW method, another exact interpolator,

Figure 1. Location map of the study area.
IDW will never predict values above the maximum measured value or below the minimum measured value. However, the Splines can predict these values. Splines are used for calculating smooth surfaces from a large number of data points. The functions produce good results for gently varying surfaces such as elevation.
OK is one of the most basic kriging methods [31]. OK assumes the model: Z(s) = μ + ε(s). Where Z(s) is the main variable of interest, and ε(s) are random errors. OK assumes stationarity of the mean and considers μ to be a constant, but unknown, value. Nonstationary conditions are taken into account by restricting the domain of stationarity to a local neighbourhood and moving it across the study area. UK assumes the model: Z(s) = μ(s) + ε(s). Where μ(s) is some deterministic function. It is not constant, but it varies smoothly within the local neighborhood, representing a local trend. The trend μ(s) is recalculated within each local neighbourhood.
These four methods were employed to compare their performances for interpolating soil properties. We compared different parameters for kriging, IDW as well as Splines, and then decided the best parameters for each technique with the smallest root mean squared error (RMSE) statistic, obtained from an independent validation data set. In kriging, spherical, exponential, and Gaussian models were fitted using the variogram. The variogram is characterized by three major properties: the nugget effect, the sill and the range. The nugget effect is a discontinuity of the variogram which expresses both the variability at a scale smaller than the sampling interval and non-spatial variation. The nugget effect cannot be removed by close sampling, but only by repeated measurements [32]. The range is the lag distance where the variance approaches an asymptotic maximum, the sill. It expresses the distance beyond which samples are uncorrelated. Once the variogram is known, the value of an attribute at any point in a mapping unit can be predicted from the available data points using kriging. Kriging gives the standard deviation of the prediction error as well. This standard deviation depends only on the variogram, the number of data and the spatial configuration with which these are taken [33] and can hence be used to determine the required number of data.
Geostatistical analyses were performed using the Geostatistical analyst extension available in ESRI ArcMap v 9.3 [34].
3.3. Validation
To validate a predictive model and choose appropriate algorithm, Cross-Validation (CV) which is a statistical method, has been used [35]. CV or so-called “leave-oneout” technique and validation with an independent data set are used for comparing the interpolation methods. CV involves eliminating each observation in turn, estimating the value at its site from the remaining observations and comparing the predicted value with the measured value [36]. This procedure is a rapid, inexpensive approach for comparing predicted and measured values [37]. Unfortunately, it has limitations in many cases. For kriging estimators, it retains the same variogram, and to be true cross validation the variogram should be recomputed and fitted afresh when each observation is removed [20]. These shortcomings can be avoided by using an independent data set for validation [20,37,38]. Validation with an independent data set, which is a superior and more dependable method, directly estimates the spatial uncertainty, as validation points are located randomly throughout the field [20,37]. However, when the sample size is small, not enough and separate data are available for modelling and validation [39]. Consequently, a modified jackknifing technique was adopted to resample the base sample data 20 times for the purpose of assessing the performance of the four methods [39]. The resampling size each time was 20 samples for validation and 126 samples for interpolation in this study.
Three indices were calculated from the measured and interpolated values at each validation sample site for each test data set. The mean error (ME), the mean absolute error (MAE) and the root mean square error (RMSE) are determined from the measured values. The ME is a measure of the bias of the interpolation which should be close to zero for unbiased methods, and the MAE as well as RMSE are accuracy measures of the interpolation which should be as small as possible for accurate interpolation [40]. The ME, MAE and RMSE were estimated for each resampled validation sets, and respectively the averages of the MEs, MAEs and RMSEs of the 20 validation sets were used to determine the performance of each interpolator.
4. Results and Analyses
4.1. Exploratory Statistics for Soil Properties
Summary statistics and the frequency distributions of soil properties are shown as a histogram in Figure 2. The histograms show a unimodel shape. The positive and small value of skewness (0.5) close to zero and kurtosis values (2.6 - 3.1) close to 3.0 indicate that the data deviated from a normal distribution [41]. Only in the case of CaCO3, does the analysis indicate that the data do not deviate from a normal distribution.
4.2. Comparison of the Interpolated Maps by the Four Techniques
The patterns of soil properties distribution produced by different interpolators using 126 points are shown in Figures 3 and 4. In the maps from the four techniques, IDW interpolation produces many Bull’s eyes on the soil surface. On the contrary, Splines have a serious oscillation problem which makes the minimum output (3.99) lower and the maximum output (6.75) higher than those of other techniques. The OK map shows rather gradual transitions with low levels of detail. Owing to its smoothing effect, the maximum value (6.00) is the lowest and the minimum value (4.53) is the highest in the four techniques.
The sampling interval (Lag) should be less than half of the range of the raw semivariogram as a rule of thumb [42]. The ratio of nugget to sill variances, expressed as percentage, can be regarded as a criterion to classify the Spatial Dependency (Sp.D) of soil parameters. If the ratio is less than 0.25, the variance has strong spatial dependency and if the ratio ranges between 0.25 - 0.75, the variance has moderate spatial dependency [43,44]. The Sp.D of soil parameters from Table 1 shows that the nugget/sill ratio ranges from 0.242 (OK-Circular) to 0.216 (UK-Exponential) for EC. For pH, the nugget/sill ratio ranges from 0.265 (OK-Spherical) to 0.096 (UKExponential). However, the nugget/sill ratio ranges from 0.030 (OK-Exponential) to 0.168 (UK-Tetraspherical) for CaCO3. These results indicate that the Exponential model for UK is the best semivariogram model to show the strong spatial dependency for the salinity variable.
4.3. Validation Results: Comparison of Interpolation Performance
Before the final surface is produced for practical use, the CV should be employed to examine how well the surface
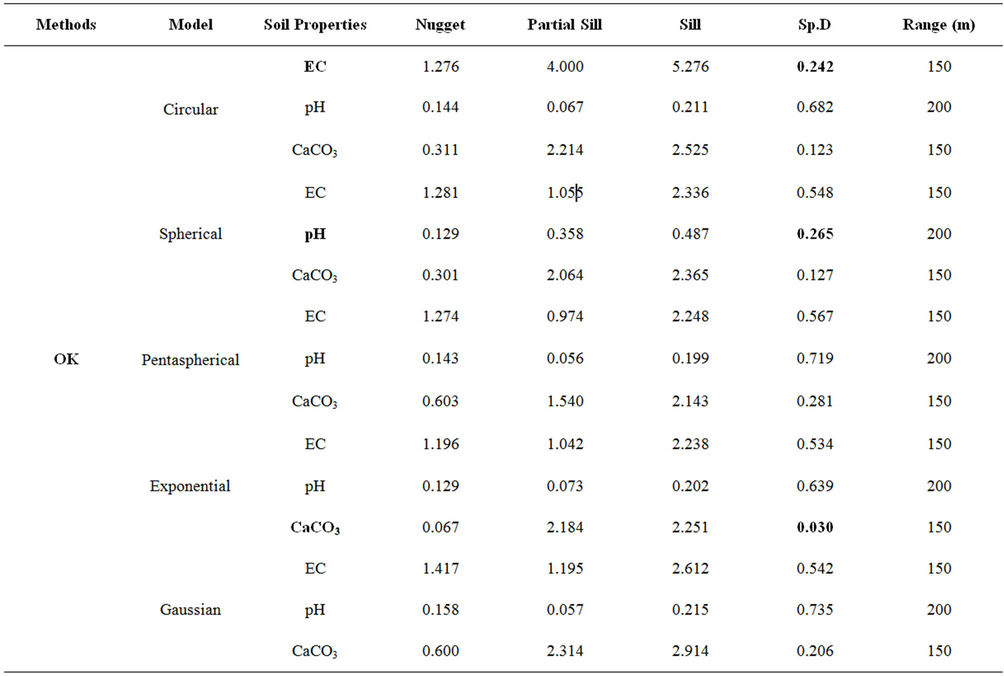

Table 1. The sampling interval (Lag), nugget, sill and spatial dependency (Sp.D) of the different interpolated methods for soil properties.
model predicts an unknown value. The CV tool uses statistical measures to assess the surface models performance. It compares measured values with predicted ones derived from the surface model. The statistical measures predict the accuracy of the surface model and its prediction map. Figure 5 provides a graphical comparison between measured and predicted values. Ideally, the predicted values should be the same as the measured ones. In reality, data points would scatter along this line due to natural variations and uncertainties. The prediction error is used to describe the difference between the prediction and the actual measured value.
Figure 5 shows that since Root-mean-square tandardized Prediction Errors for UK with spherical semivariogram are close to 1.0, this indicates that its prediction accuracies have almost comparable accuracies [45].
Considering the performance of UK in comparison with other techniques indicates a considerable improvement in prediction of soil properties.
To compare the performance of the interpolators, we calculated the mean error (ME) and the root mean square error (RMSE) of 20 validation sets as shown in Table 2. Table 2 shows that ME, which is a measure of the bias of the interpolation, is close to zero (0.0030, 0.0008 for EC and 0.0004, 0.0005 for pH by UK and OK). These data indicate that they are unbiased in interpolating the soil properties values. OK achieves slightly better ME (0.0230), comparing with UK (0.0400) for CaCO3. However, RMSEs which are accuracy measures of the interpolation should be close to 1 for accurate interpolation. Table 2 shows that RMSEs have small dispersion around the mean value for the UK and OK techniques.
Figure 6 shows other criteria of comparison using the Plot of the Quantiles (QQPlot). This indicates the quantiles of the difference between the predicted and measured values divided by the estimated kriging standard errors and corresponding quantiles from a standard normal distribution. If the errors of the predictions from their true values are normally distributed, the points should lie roughly along the dashed line [41].
The mean errors of the variables are close to zero for all the interpolation methods (Table 2). This indicates the unbiaseness of the methods. The differences between the OK and UK methods are very small. However there are more important differences among mean square errors (Table 2). The mean square errors given in Table 2 present the prediction performance of the four methods. The prediction performance is much wider than the differences in mean errors. This is because in calculating the mean errors the negative and positive bias of prediction

Figure 3. Interpolated maps of soil EC, pH, CaCO3 by (a) IDW; and (b) Splines.

Figure 4. Interpolated maps of soil EC, pH, CaCO3 by (a) Ordainary Kriging; and (b) Universal Kriging.
tends to cancel each other.
Clearly based on Table 2 and Figures 5 and 6, universal kriging is ranked the first least mean rank and its standard deviation of ranks is generally superior to other classical methods. IDW is the third accurate method with the third largest standard deviation of ranks, whereas Splines have the largest mean rank with the highest standard deviation of ranks.
The results from the Figure 6 indicate that the best model for predicting soil properties is UK with exponential semivariogram, which was used to obtain the final soil properties maps of the studied area (Figure 7). It is



Figure 7. Final interpolated maps of soil EC,ph,CaCO3 byUniversal Kriging method.

Table 2. The means of MEs and RMSEs of 20 validation sets for Kriging, IDW and Splines.
concluded that UK is the most accurate technique of the four methods for interpolating soil properties (EC, pH, CaCO3) values.
5. Conclusions
This paper reports on a study to apply a technique based on fundamental theorems of surfaces, to interpolate the spatial pattern of soil properties. The intent of this study was to provide quantitative information on soil properties and mapping methods that are in common use by the commercial sector. Our case study showed that the UK method is more accurate for predicting the spatial patterns of soil (EC, pH, CaCO3) properties than the other methods, namely OK, IDW and Splines. It is also the most accurate method when we avoid the outlier effects in assessing the performance of all methods. The generally superior performance of UK is due to less prediction errors. UK obtains the soil property surfaces without oscillation problems and Bull’s eyes. Therefore, UK can be considered as an accurate method for interpolating soil (EC, pH, CaCO3) properties. These results may help GIS specialists to select the best method for the generation of soil properties. A technique should be chosen not only for its performance on a specific soil type and data density, but also for its applicability to a wide range of spatial scales. Also another aim of the paper is to answer the question: Are soil maps dying or thriving? My answer to the question is yes and no. Yes traditional soil maps are almost dying, but, digital soil maps are now thriving.
The digital soil mapping outlined in this paper was conducted at very large map scales (over small areas). Digital soil mapping research has been most successful at the field scale because many of the soil-forming factors (climate, organisms, parent material and time) are held constant. These results lead to the future research to assess if the methodology applied in this study to map EC, pH, and CaCO3 still worked for mapping highly accurate spatial distribution of other soil properties (e.g. heavy metals). The aim is to answer the question: What is the risk assessment of soil threats e.g. heavy metals for sustainable soil resources?