A Mathematical Model for the Effect of Enzymes on Metabolism of Pharmacologically Active Substances ()
1. Introduction
The presence of certain substances in the fluid mass of the body can affect neural responses, altering perception and the ability to function. These substances include alcohol, nicotine, opioids, cannabis, and caffeine. When such a substance reaches the nervous system, they bind to receptors of neurotransmitters, altering the normal operation of neurons. They are removed from the body by various paths, but most of them are degraded by enzymes to substances that can be digested or eliminated. One such path involves cytochromes P450 (CYPs), a superfamily of hemeproteins. CYPs are the terminal oxidase enzymes in electron transfer chains.
The mechanism(s) of addiction are being studied [1] [2]. The model studied here has one mechanism for change in substance processing, namely modification of catalylic process by changes of enzyme level. Other research has focused on the mechanism of repeated drug exposure in altering the activity of individual neurons and synapses within the brain, thereby changing the reward circuitry to cause addiction.
In this paper, we derive and study a model for the competition between metabolic processing (degradation by enzymes) and pharmacokinetics (receptor binding) of psychoactive substances.
1.1. Psychoactive Substances
Addiction is a potentially dangerous affliction that often involves repeated ingestion of a psychoactive substance [3] [4] [5]. The substance is ingested, processed into the circulation system by the body, binds reversibly to neural receptors in the central nervous system, and eventually is metabolized and excreted.
Many substances fit in this rubric. They include ethanol, opioids, tetrahydrocannabinol (THC), amphetamines, cocaine, nicotine, and caffeine. In Appendix A, we summarize the dynamics of these substances.
1.2. Use Patterns
Psychoactive substances can be introduced in the body through injection or through absorbing tissues (lungs, gastro-intestinal tract). Once in the body, they make their way to the bloodstream, whence they can diffuse through capillaries to bind with receptors on neurons, where the psychoactive effects are experienced. Binding of these substances on the receptors changes the way of the recptors function, and thereby changes the neural response of the taker.
Addiction can result from repeated exposure to a pharmacologic substance if the resulting neural alterations are interpreted as a rewarding stimulus, in spite of any adverse consequences. Two properties characterize addictive stimuli: 1) they are reinforcing, i.e., they cause the user to seek repeated exposures; and 2) they are intrinsically rewarding, i.e., they result in feelings of pleasure for the user.
The goal of this paper is to derive a model for the dynamics of the metabolism and receptor binding, and to extract qualitative and quantitative information from it.
Drew [6] has proposed and analyzed a model for the metabolic chemistry of carbohydrates, fats and proteins, which shows that the qualitative dynamic depends on enzyme levels. He also suggests a model for the evolution of the level of enzymes.
In this paper, we posit a model for the reversible binding of a species to neural binding sites, and its enzymatic metabolism. We use this model to examine the behavior of system levels of the species under several different dosage scenarios. We also discuss how enzyme dynamics can affect the overall levels of systemic species levels.
This model should be regarded as somewhat more than qualitative, but not quite quantitative. First, the actual metabolic reactions are more complex than represented in Figure 1 (e.g., Cederbaum [7] ), with several subspecies produced and further reduced in each reaction represented there. Further, most, if not all, of the reactions are catalyzed by more than one enzyme. And finally, the “reverse” reactions are actually more complicated reactions that are not simply splitting or reuniting of the species displayed.
2. Enzyme-Controlled Mass Action Model
We posit a mass-action chemistry model (see Figure 1) for the evolution of a serum and receptor-bound substance. Let
be the abundance of unbound ethanol, and
be the abundance of the receptor-bound substance at time t.
The reaction structure is shown in Figure 1. The substance is supplied at rate
, bound to the receptors at rate
, released from the receptors at rate
, and converted to an excretable form by its targeting enzyme at rate
.
The enzyme-assisted metabolic reaction is discussed in entry-level biochemistry texts (see, for example, Berg, et al. [8] ). The model that we use is
(1)
(2)
where Q is the rate of ingestion of substance S, BR is the abundance of bound receptors. The rate of binding of the substance to neural receptors
and the rate of unbinding of bound receptors is
, where
is the total abundance of receptors.
Here E3 is the abundance of the metabolizing enzyme, K3 is its dissociation constant and
is its conversion rate. For simplicity in calculations, we write
, and refer to
as the effective conversion rate. In the context of this model, we expect that consuming the substance causes a spike in the serum level, pushing it far above the levels of the enzyme that metabolizes it to an excretable form. In this case, the Hill’s model saturates, with almost all of the enzymes bound to substrate molecules, so that the rate of conversion is nearly constant. As the reactions proceed, the species level falls so that not all enzymes are bound, and the conversion rate depends on abundance.
We note that if enough of the receptors are bound to the substance affecting neuron behavior, the central nervous system fails to function properly, and the individual could lose consciousness and/or die. Thus, we assume that
. We further write
.
2.1. The Pharmacokinetic-Metabolic Model
With these assumptions, the equations for the evolution of serum and bound pharmacokinetic substance become
(3)
(4)
2.2. Scaling
Let
(5)
Then the equations become
(6)
(7)
A reasonable scaling for the source Q is to balance it with degradation, so that we choose
(8)
We choose the scale for substance concentration to be the value that maximizes the degradation rate. This value is
(9)
Also, we choose the time scale to correspond to the time scale implicit in requiring the time derivative term in Equation (6) to balance with degradation. Thus
(10)
Finally, we choose the scale for BR by balancing the binding and release of substance from receptors, so that
(11)
The scaled equations become
(12)
(13)
The two parameters
and
are, respectively, the rates of attachment to, and release from receptor per degradation. Thus, they represent the relative importance of attachment and release. Substituting and dropping the primes gives the dimensionless pharmacokinetic-metabolism (PKM) model:
(14)
(15)
3. Solutions
In this section, we shall discuss some solutions of the equations and how they inform substance use and abuse. All numerics performed in this Section were accomplished with MAPLETM.
3.1. Steady Solutions
Note that if Q is constant and
, there is a steady-state solution with
, and
(16)
Note that this solution does not exist if
. Within the dynamics represented by the model, if
, the degradation of S cannot convert substance to inactive fast enough, and consequently substance builds up in the system.
3.2. Initial Value Problem: Response to a Dose
If the system has no residual substance (including molecules bound to receptors) and is subjected to a dose of substance at time
, that dose will bind reversibly to receptors and degrade. To model this, let us examine the behavior of the model for
, with an initial dose of
,
.
The model is two-dimensional and autonomous. The physical problem requires that the dependent variables be non-negative. The positive quadrant in S-BR space is filled with solution trajectories that do not cross, and do not exit. All solutions to the initial value problem approach the origin.
Figure 2 shows typical numerical solutions to the initial value problem specified by equations (14) and (15) with initial conditions
, for
and 4, and
, with binding and release rates
and 2.0 and
and 2.0. We chose these values as “low” rates (0.2) and “high” rates (2.0).
All of these solutions start at
at the highest substance (S rightmost) value with no bound receptors (BR = 0). The model predicts that the substance level decreases monotonically, while the bound receptor level increases at first, reaching a maximum value, then decreases. The ultimate state with no substance remaining and no bound receptors is approached exponentially slowly. The initial level of substance,
, represents the dose. The subject experiences an
![]()
Figure 2. Evolution of doses with S(0) = 1.0, 2.0, 3.0, 4.0 with different binding rates τa and release rates τr as indicated. Larger doses S(0) result in larger intoxication maxBR. Note that the vertical axes for the different rates are not the same.
increase of intoxication (BR rising) for a time, with the intoxication level reaching a maximum, then decreasing to no intoxication in infinite time. The maximum value of bound receptors corresponds to maximum interference with the normal operation of neurons. We shall refer to this value as lethality. Note that there are no finite singular points in the first quadrant.
Note that there are trajectories in the first quadrant with
,
on the positive vertical axis These trajectories will enter the quadrant (i.e.,
), reach a maximum value of S (with
), and exponentially approach the origin. These solutions also approach one of the dose processing solutions (above). We offer no further analysis of these solutions since it is not clear that such an initial condition can be attained by the subject.
3.3. Periodic Dosing
Let us consider the solution with periodic dosing of the type
(17)
where Δ is the dose, T is the dose interval, and δ is the Dirac delta-function. Specifically, the subject rapidly ingests an amount of substance
at times
. That dose binds to available receptors, and is degraded. The solution will be periodic if the “next” dose is taken at the time that the level of bound receptors returns to the level at which the previous dose is ingested. Specifically, the solution will be periodic if
(18)
Figure 3 shows a periodic solution with dosing given by (17). Figure 4 shows several periodic solutions for different values of
for
.
Note that for any positive threshold value
, there is a relationship between the dose Δ and dosing interval T, corresponding to a unique periodic solution. This relation is illustrated in Figure 5. Likewise, there is a relation between dose Δ and lethality
. This relation is illustrated in Figure 6.
![]()
Figure 3. Periodic solution with a Dirac delta-function dose of
at times t = 0, T, 2T, 3T, ∙∙∙.
![]() (a) (b)
(a) (b)
Figure 4. Illustration of six periodic solutions for parameter values τa = 2.0, τr = 0.2 corresponding to dose processing shown in Figure 2(c). (a) Periodic solutions based onS(0) = 4.0; (b) Periodic solutions based on S(0) = 2.0.
![]()
Figure 5. Correlation of dose Δ and interval T for different threshold intoxication BR.
![]()
Figure 6. Correlation of dose Δ and lethality BRmax for different threshold intoxicationBR.
4. Tolerance
Tolerance [4] [5] [9] 1 occurs when a doses of given size do not lead to the same psychological effect. Tolerance can be classified as pharmacokinetic (metabolic tolerance) or pharmacodynamic (functional tolerance). Metabolic tolerance occurs when repeated dosing causes the dose to be degraded more rapidly than in a naive user. Functional tolerance results when binding substance molecules are less effective in altering neurological function.
The model developed in Section 2 is capable of providing quantitative information on both types of chronic tolerance. Metabolic tolerance can be described by an increase of the enzyme level, which can then result in more rapid degradation of the substance. We discuss this effect in Section 4.1 below.
Functional tolerance can be accounted for in the model by the level of receptors. An increase in the number of receptors would cause a lower level of bound receptors in response to a given dose, since the dose would not inhibit as many receptors. In addition, substance molecules would bind to more rapidly due to the increase in the number of receptors.
4.1. Effect of Enzyme Level
We note from the model definitions and nondimensionalization in Sections 2 that the level of the degradation enzyme is involved in modeling the pharmachological parameters. Enzymes assist most of the known metabolic reactions, and help control and/or facilitate reactions. Indeed, many metabolic reactions would not occur without enzyme assistance.
The model summarized in Appendix B suggests that usage of the enzyme can cause it to have a higher level in the body than if it is not utilized. The idea is that functioning enzymes (which are essentially proteins) are less likely to be degraded than idle ones. This further suggests that the level of the degradation enzyme will increase during periodic substance ingestion. Thus, continued use of a substance will lead to faster degradation, which can be interpreted as increased tolerance.
In order to examine the effect of increasing enzyme level, we write the model as
(19)
(20)
where ΔE is the change in enzyme level. It seems reasonable to assume that the enzyme level increases slowly compared to the clearing time for a dose; consequently, we shall assume that ΔE is a constant.
4.2. Effect of Receptor Level
In order to model the effects of an increase of bound receptors, we write
(21)
(22)
where ΔR is the fractional change in the level of receptors. Note that the (dimensionless) rate of binding is
.
Again, we seek periodic solutions with
.
Figure 7 demonstrates that an increase in the level of the enzyme causes the maximum lethality to decrease, indicating that the dose is less effective.
Figure 8 shows that increasing the dose can compensate for an increase of enzyme level.
Figure 9 shows the calculated increase in the lethality as a function of the fractional increase of receptor level.
Figure 10 shows the changes in dosing interval as a function of the fractional increase of receptor level, for different minimum intoxication levels
.
![]()
Figure 7. Correlation of lethality BRmax for increasing enzyme level ΔE.
![]()
Figure 8. Correlation of interval T with increasing enzyme level ΔE for different threshold intoxication BR.
![]()
Figure 9. Correlation of lethality BRmax for increasing receptor binding rate ΔR.
![]()
Figure 10. Correlation of interval T for increasing receptor binding rate ΔR.
We see that the lethality (maximum value of bound receptors) increases with increasing receptors due to the more rapid binding of substance to receptors. Moreover, increasing the number of substance molecules bound to receptors means that the substance molecules are not available to the degradation reaction. Consequently, the frequency of dosing decreases, since the substance molecules remain bound to the receptors, delaying the time to reach their initial level
.
5. Discussion
We have posited and analyzed a model for the systemic evolution of a psychoactive substance and its state of being bound to neural receptors. The model assumes that the substance molecules are bound and released from the binding sites according to mass action dynamics, and are degraded by an enzyme while in the unbound state. The model predicts a single maximum in numbers of bound states during a single dose. It also shows the behavior when a fixed dose is applied to the system periodically. In this situation, the substance-bound site system follows one of the trajectories corresponding to a single (larger) dose which is allowed to metabolize completely, with a jump in substance level after the number of bound sites reduces to its initial level.
This model allows the analysis of how the outcome depends on important metabolic parameters, e.g., period, dose, and bound state level. One important parameter is the level of the metabolizing enzyme. We also note that the level of the metabolizing enzyme depends on the usage, through the action of protein degradation mechanisms. A model for this process is presented in Appendix B.
One disadvantage in working in this area of system molecular dynamics is that rates for various subprocesses are not known. One value of a quantitative model is that can suggest experiments that couple parameters to results and, indeed, confirm or refute the validity of the model itself. Complicating this further is that defining rates depend on individuals, and on whether the processes occur in organs (and therefore must be transported into that organ) or in the blood or gut.
A mathematical model can aid in the analysis of processes that normally are explained in qualitative terms. Such a model uses mathematical concepts and language to explain a phenomenon, to study the effects of different parameters, and to make predictions about its behavior. The model studied here for substance-bound sites formulates the chemistry of psychoactive metabolism as a set of differential equations and predicts how outcome depends on parameters. Specifically, the model shows the number of parameters that must be determined for use as a predictive tool for an individual, and how combinations of the parameters relate to solutions. In particular, a central feature of the model is the dependence of rates and psychoactive levels on enzyme levels. This recognition may suggest control of addiction and/or tolerance by varying enzyme levels.
Finally, we mention one complication that illustrates the major simplification in the model developed and studied in this paper. The present model assumes metabolism controlled by one enzyme. Actually, there are several rate controlling steps in such processes. The pharmokinetics and metabolism of ethanol is a well-studied process.
Ethanol is a chemical compound with formula C2H5OH. When it is consumed, it quickly passes through the gastric-blood boundary and is carried by the circulatory system to all parts of the body. Ethanol causes impairment of neurocognitive function by binding to GABA. While the pharmacodynamics of ethanol are not fully understood, it appears likely that ethanol works ion channels in the central nervous system by binding to GABAA receptors, thereby affecting their function.
Ethanol binds with the digestive enzyme alcohol dehydrogenase, which transforms it into its metabolite acetaldehyde (ethanal). Acetaldehyde is subsequently metabolized by the enzyme aldehyde dehydrogenase into acetate, which in turn is converted to carbon dioxide and water. Acetate also combines with coenzyme A to form acetyl-CoA, which can enter into the Krebs cycle. Alcohol dehydrogenase and aldehyde dehydrogenase are present in high concentrations in the liver, but are present throughout the body.
In spite of the complexity of this process, we feel that the simplified model presented herein captures the essence of the binding mediated metabolism of psychoactive substances.
Maple is a trademark of Waterloo Maple Inc.
A. Psychoactive Substances and Pathways
In this appendix, we discuss the binding and metabolization of several common psychoactive substances.
Ethanol is regulated substance that is in common use throughout the world. It is absorbed through the gastro-intestinal wall where it binds with the enzyme alcohol dehydrogenase, which transforms it into its metabolite acetaldehyde (ethanal). Ethanol interacts with a neurotransmitter called γ-aminobutyric acid, or GABA, which suppresses the activity of the central nervous system.
Opioids constitute a class of drugs that includes codeine, morphine and fentanyl. Opioids bind to specific opioid receptors in the nervous system and other tissues. There are three principal classes of opioid receptors, μ, κ, and δ.
Tetrahydrocannabinol (THC) is the principal psychoactive constituent of cannabis. THC binds to the cannabinoid receptor CB1 which is found in the central nervous system. THC is metabolized mainly in the liver by cytochrome P450 enzymes, and is excreted.
Amphetamines are metabolized by enzymes CYP2D6, dopamine-hydroxylase (DBH) and flavin-containing monooxygenase 3 (FMO3). Amphetamine affects neural function by binding trace amine-associated receptor 1 (TAAR1), a G protein-coupled receptor, increasing its activity by causing dopamine to be released.
Cocaine affects the central nervous system by binding dopamine transporter proteins, which recycle dopamine transmitter released during neural signaling. Cocaine is metabolized by cholinesterase enzymes (primarily in the liver and plasma).
Nicotine binds to nicotinic acetylcholine receptors in the brain, increasing the levels of several neurotransmitters in various brain structures, thereby eliciting its psychoactive effects. Nicotine is metabolized in the liver by cytochrome P450 enzymes (mostly CYP2A6, and also by CYP2B6).
Caffeine is a widely consumed psychoactive drug which stimulates the central nervous system. It binds to adenosine receptors preventing adenosine from activating them by blocking the location on the receptor where adenosine binds to it. In the brain, adenosine receptors slow metabolic activity by a combination of actions. Presynaptically, it reduces synaptic vesicle release while post synaptically it has been found to stabilize the magnesium on the NMDA receptor. Caffeine is metabolized bythe cytochrome P450 oxidase enzyme system, in particular, by the CYP1A2 isozyme, into three dimethylxanthines. This occurs in the liver.
B. Enzyme Dynamics
In this Appendix, we summarize a metabolism model derived by Drew [6] for the level of an enzyme involved in a Michaelis-Menten reaction [10], see also Lin & Segel [11]. The model assumes that enzyme molecules are synthesized by ribosomes (Drew [6] ), are activated by a process that we do not specify here, and degraded by proteolysis. The model further assumes that only enzymes which are not bound to substrate are subject to degradation by proteolysis.
The model in Figure 11 is a modification of the classical Michaelis-Menten model, adding an activation step for the enzyme. In this model, the substrate molecule S is catabolized by an activated enzyme E+. It is then available to bind reversibly with the substrate molecule to form the complex, EC. The complex can then release the substrate without finishing the reaction, or it can go irreversibly to completion, making a product moleculeB and releasing the inactive enzyme. We shall assume that these reactions change the amount of each of the several substances according to the following mass action reaction equations.
(23)
(24)
(25)
(26)
(27)
Here Q is the input rate of the substance, QE is the rate at which the enzyme is manufactured by the body. In addition, we assume that inactive and activated enzyme molecules are degraded at rates
and
, respectively. We note that the rate of production of the enzyme should depend on the availability of appropriate amino acids for protein manufacture, and may be controlled by the presence or absence of other molecules.
In order to obtain the long-term behavior of this system, let us assume the S-BR subsystem proceeds much faster than the enzyme evolution. Specifically, we assume that Equations (26) and (27) are in equilibrium. The system reduces to
(28)
(29)
![]()
Figure 11. Enzymatic Reactions. S is the substance molecule, BR is the substrate molecule bound to a receptor, E is the inactive enzyme, E+ is the activated enzyme, EC is the enzyme-substrate complex, and S− is the degraded substance.
(30)
(31)
(32)
Using Equation (32) in Equation (31) yields
(33)
which can be used to eliminate
from Equations (29) and (30), resulting in
(34)
(35)
(36)
Let us average the system over a long time interval
. For any of the time derivative terms of the enzyme in its various forms, we have
(37)
as
. Then we have
(38)
(39)
(40)
(41)
(42)
where the overline denotes the time average. Then
(43)
(44)
(45)
and
(46)
The total amount of the enzyme in its various forms is
(47)
According to this model, the steady-state level of enzyme depends on how rapidly substrate is supplied. Assume, for the moment, that the effect of substrate supply, Q, is negligible. Then Equation (47) is
(48)
We denote
 (49)
(49)
This is the level of enzyme a result of the organism synthesizing the enzyme (at rate Q) and destroying the enzyme (at rate ), modulated by the rate of moving into the activated state (expressed by
), modulated by the rate of moving into the activated state (expressed by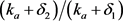 ). Further, let
). Further, let
 (50)
(50)
Then the enzyme level can be written as
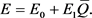 (51)
(51)
This model supports the assertion that the enzyme level is increased by the utilization of the enzyme (Equation (51)). Thus, using the mechanism of this particular metabolic process makes it more efficient.
NOTES
1There are two distinguishable types of tolerance in the psychokinetic literature, acute and chronic. Acute tolerance is characterized by a diminished physiological effect of a single dose. Chronic tolerance results from repeated dosing, and is characterized by a diminished response to a given dose.