Permanent Fault Identification Method for Single-Phasea Adaptive Reclosure of UHVAC Transmission Line ()
1. Introduction
Most faults in UHVAC transmission system are single phase transient fault [1]. In the traditional automatic re-lock, if the coincidence of permanent fault, the system will cause the two shock, and even make the system crash. In 1980s, Professor Ge Yaozhong put forward the idea of “adaptive reclosure” [2] arousing wide attention of experts and scholars in electrical engineering from domestic and foreign. A wealth of achievements have been made in the study of the two arc characteristics [3], the voltage characteristics [4] [5], the current characteristics of shunt reactor [6] [7] [8] and the characteristic of model parameters [9] [10]. The practical application is difficult since neural network based on the need to train a large number of samples [11] [12]. The criterion based on arc criterion and voltage is difficult to realize since the shunt reactor technology is widely used in the super high voltage, which accelerates the arc quenching process and limits the amplitude of the fault voltage [13].
Based on the analysis of the characteristic of single-phase permanent fault phase voltage after tripping ,this paper proposes method for distinguishing single phase permanent fault based on steady-state component frequency acquired through two order derivative of the fault phase voltage signal and the ratio of the original signal.
2. Analysis on the Characteristics of Fault Phase Voltage during Single-Phase Permanent Fault after Tripping
During the single-phase permanent fault, fault phase voltages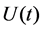 
is composed of the steady state component and the transient component, the expression was as follows:
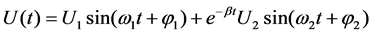(1)
In the formula: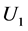
, 
, 
represent voltage amplitude, frequency and phase steady components respectively, 
, 
, 
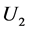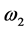represent the amplitude, frequency and phase of transient component respectively,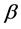 
is transient attenuation coefficient.
Due to the fault point to ground reliable discharge, the transient component will decay rapidly to zero, after entering the steady state, its expression is:
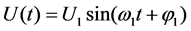(2)
After two order derivative of the formula (2):
(3)
and then
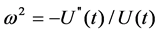(4)
So the steady state component frequency f is:
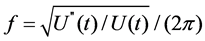(5)
Because the steady state component is mainly determined by the sound phase capacitance coupling voltage and the electromagnetic coupling voltage [14], the steady state frequency f is close to the frequency of the power frequency f0. Based on the above analysis, the relations between steady state component frequency and frequency as following:
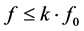(6)
In the formula, k represents reliability coefficient. After a lot of simulation, the author found that the 1.3 is suitable in considering the line model equivalence and simplification of the simulation software, actual gap between f and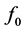
.
3. Discriminant Principle
In the sine function, the data in the 1/4 continuous period can reflect the data of the whole cycle. Two arc durations are about 200 ms during transient fault [15]. Considering the above two aspects, this paper focuses on 200 ms time period after trip and calculates the data from power system, if calculate data in 1/4 continuous power frequency period satisfied formula of (5), the fault is determined as a permanent fault. Otherwise, it will be judged as instantaneous fault. Criteria flow chart is shown in Figure 1.
4. Simulation Results and Analysis
As shown in Figure 2, the simulation model is based on the model of 1000 KV UHV line system in the southeast Nanyang. Line length is 358 km. Parameters of this line are as following:
![]()
Figure 2. Model of 1000 KV UHV transmission line system in Southeast Nanyang.
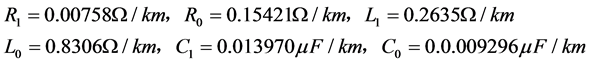
System parameters at both ends are:
![]()
, ![]()
, ![]()
, ![]()
.
Parameters of shunt reactor:
![]()
Parameters of neutral point small reactor:
![]()
.
Permanent single-phase grounding fault occurs of system in 0.5 s, tripping in 0.1 s, and the sampling frequency is 10 kHz. The calculation results show that the power angular phase difference are 0˚, 10˚, 20˚, 30˚, 40˚, 50˚ respectively, the transition resistances are corresponding to![]()
, ![]()
, ![]()
, ![]()
, ![]()
, the fault distance is the line (from the M side) 0%, 25%, 50%, 75%, 100% corresponding to a total of 150 cases can be accurately identified.
Table 1 and Table 2 are discriminant success time when![]()
,![]()
.
From Table 1 we can make conclusion that when the power angle difference and transition resistance are constant, discriminant success time showing such a regularity that increase first and then decrease with increasing of L. When the power angle difference and the fault location is certain, discriminant success time shows decreasing trend with increasing of R. From Table 2 we can also seen that when the fault position and the transition resistance are at a certain time, discriminant success time showing such a regularity that increase first and then decrease with increasing of θ.
By a lot of simulation data can be seen that in the UHV AC transmission system in the occurrence of a permanent fault occurs, the duration of transient component is 180 ms - 55 ms after tripping.
4. Conclusions
In this paper, based on the analysis of fault phase voltage characteristics of single-phase permanent fault, this paper presents a method to determine the frequency of steady state component based on the ratio of the two derivative of the
![]()
Table 1. Criterion flow chart successful time table when![]()
.
![]()
Table 2. Successful time table when![]()
.
fault phase voltage and the ratio of the fault phase. The method is simple, high reliability and strong adaptability, and a lot of simulation results verify that the proposed criterion is also suitable for 500 kV ultra high voltage transmission line.
The deficiency of this criterion is that:
1) Although this criterion can accurately identify the fault, the discriminant success time affected by transition resistance relatively large; 2) Due to the use of the ratio method, the denominator (fault phase voltage) may be zero, but not appear in the simulation.