Impact of Tropospheric Delay Gradients on Total Tropospheric Delay and Precise Point Positioning ()
Received 3 April 2016; accepted 15 May 2016; published 18 May 2016

1. Introduction
The tropospheric layer represents the lower part of the atmosphere, which extends up to 50 km from the earth’s surface [1] . Tropospheric layer causes delay to the signal, which is known as tropospheric delay. Unfortunately, the effect of troposphere is equal on both code and carrier phase. This is why tropospheric effect cannot be eliminated while maintaining geometry using linear combinations between observables. Tropospheric delay depends on pressure, humidity, and temperature along the propagation path of the signal. Generally, tropospheric delay is minimum when the satellite is at the user’s zenith, and is maximum when the satellite is near the user’s horizon.
Typically, tropospheric delay can be divided into two components, namely, dry and wet component. The dry component represents 90% of the total delay, while the wet component represents 10% of the total tropospheric delay [2] . However, the horizontal gradients are usually neglected. The main reason of the wet tropospheric delay is the water vapor in the lower part of the tropospheric layer, 11 kms from sea level, and it contains most of the water vapor. Modeling of the wet delay component is difficult because of the water vapor density is variable with both position and time. The average total zenith troposphere delay varies between 2.3 and 2.6 m [3] . Unlike the dry component, the wet component is highly correlated with the total tropospheric delay [4] ; hence the wet component is highly correlated with the station height [5] . The tropospheric delay components (dry and wet) are usually modeled at zenith and then mapped to the corresponding satellite elevation angle using an elevation angle dependent mapping function as follows [6] :
 (1)
(1)
 (2)
(2)
where  is the total zenith tropospheric delay,
is the total zenith tropospheric delay, 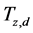 is the zenith dry component of total zenith tropospheric delay,
is the zenith dry component of total zenith tropospheric delay,  is the zenith wet component of total zenith tropospheric delay,
is the zenith wet component of total zenith tropospheric delay,  is the dry mapping function,
is the dry mapping function, 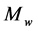 is the wet mapping function,
is the wet mapping function,  and
and 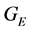 are the northern and eastern horizontal delay gradients,
are the northern and eastern horizontal delay gradients,  is the tropospheric gradient mapping function,
is the tropospheric gradient mapping function,  is the satellite azimuth, and E is the satellite elevation angle.
is the satellite azimuth, and E is the satellite elevation angle.
Equation (1) divided the total tropospheric delay into three components. The first is the dry component, the second is the wet component, and the third part accounts for the azimuthal dependence of tropospheric delay with the introduction of the horizontal gradients 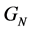 and
and  in the North-South and East-West directions, respectively [7] . Different models are available to compute the zenith tropospheric delay (dry and wet components). Tropospheric models include Saastamoinen model [8] , Davis et al. model [9] , Baby et al. model [10] , Hopfield model [11] , and NOAA tropospheric model [4] . Mapping functions, on the other hand, include Chao mapping function [12] , Davis mapping function [9] , Herring mapping function (MTT) [13] , Niell mapping function (NMF) [14] , and Vienna mapping function (VMF1) [15] . For more details about other tropospheric models and mapping functions, refer to [16] and [17] . This paper is organized to cover different aspects about tropospheric delay, tropospheric gradients, and precise point positioning. Section 2 introduces the PPP mathematical model. Section 3 is devoted to describing the data used in this paper. Sections 4 and 5 cover the impact of tropospheric gradients on total tropospheric delay estimation and PPP solution, respectively. Section 6 summarizes the main paper conclusions.
in the North-South and East-West directions, respectively [7] . Different models are available to compute the zenith tropospheric delay (dry and wet components). Tropospheric models include Saastamoinen model [8] , Davis et al. model [9] , Baby et al. model [10] , Hopfield model [11] , and NOAA tropospheric model [4] . Mapping functions, on the other hand, include Chao mapping function [12] , Davis mapping function [9] , Herring mapping function (MTT) [13] , Niell mapping function (NMF) [14] , and Vienna mapping function (VMF1) [15] . For more details about other tropospheric models and mapping functions, refer to [16] and [17] . This paper is organized to cover different aspects about tropospheric delay, tropospheric gradients, and precise point positioning. Section 2 introduces the PPP mathematical model. Section 3 is devoted to describing the data used in this paper. Sections 4 and 5 cover the impact of tropospheric gradients on total tropospheric delay estimation and PPP solution, respectively. Section 6 summarizes the main paper conclusions.
2. PPP Mathematical Model
The mathematical models of GPS observables can be summarized as follows [18] :
 (3)
(3)
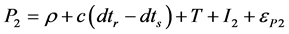 (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
where ![]() are the pseudorange (code) measurements on L1 and L2, respectively;
are the pseudorange (code) measurements on L1 and L2, respectively; ![]() are the carrier-phase measurements on L1 and L2, respectively, scaled to distance (m);
are the carrier-phase measurements on L1 and L2, respectively, scaled to distance (m); ![]() are the satellite and receiver clock errors, respectively;
are the satellite and receiver clock errors, respectively; ![]() are the corresponding wavelengths for carrier phase frequencies L1 and L2, respectively;
are the corresponding wavelengths for carrier phase frequencies L1 and L2, respectively; ![]() are the ambiguity integer numbers of L1 and L2 ambiguities, respectively; c is the speed of light in vacuum (m/sec);
are the ambiguity integer numbers of L1 and L2 ambiguities, respectively; c is the speed of light in vacuum (m/sec); ![]() is the true geometric distance between satellite antenna phase center and receiver antenna phase center at reception time (m);
is the true geometric distance between satellite antenna phase center and receiver antenna phase center at reception time (m); ![]() are the L1 and L2 ionospheric delay, respectively; and
are the L1 and L2 ionospheric delay, respectively; and ![]() are the unmodeled errors including residual orbital error, hardware delay, and multipath effect.
are the unmodeled errors including residual orbital error, hardware delay, and multipath effect.
The first-order ionosphere free linear combination can be formed as follows:
![]()
![]() (7)
(7)
![]() (8)
(8)
where ![]() are the first-order ionosphere-free code and carrier phase combinations,
are the first-order ionosphere-free code and carrier phase combinations, ![]() are the first-order ionosphere-free combination of
are the first-order ionosphere-free combination of ![]() and
and![]() , respectively;
, respectively;![]() ,
, ![]() ,
, ![]() , and
, and ![]()
Total tropospheric delay can be estimated from Equations (7) and (8) either considering tropospheric gradients or neglecting the tropospheric gradients. This paper examines the effect of tropospheric gradients on the total troposphere estimation and on PPP solution. In the first case, the coordinates of stations are kept fixed to their actual values and the tropospheric delay is estimated twice, with and without tropospheric gradients. In the second case, the station position is estimated along with the total tropospheric delay.
3. Data Description
4. Impact of Tropospheric Gradients Estimation on Total Tropospheric Delay
To investigate the effect of tropospheric gradients estimation on the total tropospheric delay, the coordinates of
![]()
Figure 1. GPS stations used to study tropospheric gradients effect.
stations are held fixed to their actual values during the processing. The tropospheric error is modelled according to Equations (1) and (2). The estimated total tropospheric delay is compared with the IGS published values. Figure 2 and Figure 3 show the estimated total tropospheric delay when the tropospheric gradients are considered and when it is neglected compared with the IGS published total tropospheric delay.
As seen in Figure 2 and Figure 3, the PPP-based estimated total tropospheric delay is comparable with the IGS published values. However, there is a bias in both cases. To study the bias of the estimated total tropospheric delay, the difference between the IGS published values and the estimated values are computed as seen in Figure 4 and Figure 5 for both stations as examples.
Figure 4 and Figure 5 show that modeling tropospheric gradients reduces the error in the estimated total tropospheric delay. Moreover, the bias in the estimated total tropospheric delay is reduced when modeling the tropospheric gradients. Table 1 summarizes the bias and the corresponding standard deviation (STD) in the estimated total tropospheric delay for all stations.
As seen in Table 1, the average bias of the estimated total tropospheric delay when neglecting tropospheric gradients ranges from −1.72 mm to 2.14 mm while the average bias when estimating gradients are −0.898 mm to 1.92 mm which means that the bias is reduced by about 30%. Moreover, the average standard deviation of the bias is 4.26 mm compared with 4.52 mm which means that the standard deviation is improved by about 6%.
5. Effect of Tropospheric Gradients on PPP Solution
To investigate the effect of tropospheric gradients on PPP solution, hourly data during January 2015 of the same stations is used. The coordinates are estimated twice, when neglecting the tropospheric gradients and when estimating the tropospheric gradients along with other parameters. Figures 6-11 show latitude, longitude, and ellipsoidal height error for RAMO and KIRU IGS stations in both cases as examples.
Our results showed that estimating the tropospheric gradients improves the estimated coordinates for all stations. Generally, the improvement in the height coordinates is much more than the improvement in the horizontal coordinates (latitude and longitude). Coordinates solution is almost the same for the first 10 minutes till the tropospheric parameters are separated from other unknown parameters. However, after the first 10 minutes the solution behaves better when estimating the tropospheric gradients. Table 2 summarizes the effect of tropos-
![]()
Figure 2. Impact of neglecting tropospheric gradients on total tropospheric delay estimation at PALM IGS station.
![]()
Figure 3. Impact of neglecting tropospheric gradients on total tropospheric delay estimation at SYOG IGS station.
![]()
Figure 4. Estimated total tropospheric delay error at PALM IGS station.
![]()
Figure 5. Estimated total tropospheric delay error at SYOG IGS station.
![]()
Table 1. Effect of tropospheric gradients on the estimated total tropospheric delay.
pheric delay estimation on the root-mean-square (RMS) of the estimated coordinates.
6. Conclusion
In this paper, one month of GPS data collected from ten IGS stations is used to investigate the effect of modeling tropospheric gradients on the estimation of the total tropospheric delay and station position. In the first case,
![]()
Figure 6. Effect of tropospheric gradients on latitude errors at RAMO IGS station.
![]()
Figure 7. Effect of tropospheric gradients on longitude errors at RAMO IGS station.
![]()
Figure 8. Effect of tropospheric gradients on height errors at RAMO IGS station.
![]()
Figure 9. Effect of tropospheric gradients on latitude errors at KIRU IGS station.
![]()
Figure 10. Effect of tropospheric gradients on longitude errors at KIRU IGS station.
![]()
Figure 11. Effect of tropospheric gradients on height errors at KIRU IGS station.
![]()
Table 2. Effect of tropospheric gradients on coordinates estimation.
the coordinates of stations are kept fixed to their actual values and the tropospheric delay is estimated twice, with and without tropospheric gradients. In the second case, the station position is estimated along with the total tropospheric delay with and without tropospheric gradients. It is shown that the average bias of the estimated total tropospheric delay when neglecting tropospheric gradients ranges from −1.72 mm to 2.14 mm while the average bias when estimating gradients are −0.898 mm to 1.92 mm which means that the bias is reduced by about 30%. In addition, the average standard deviation of the bias is 4.26 mm when the tropospheric gradients are estimated compared with 4.52 mm when the tropospheric gradients are neglected, which means that the standard deviation is improved by about 6%. Moreover, the improvement in the estimated coordinates RMS is as low as 1 mm.