A Concise Model and Analysis for Heat-Induced Withdrawal Reflex Caused by Millimeter Wave Radiation ()
1. Introduction
Millimeter wave (MMW) is a subset of radio frequency (RF) in the 30 - 300 gigahertz (GHz) range. Human body exposure to MMW radiation at sufficiently high intensities increases the skin temperature and induces thermal pain. Since the energy penetration depth of MMW irradiation in tissue is very shallow (millimeter or less), the primary effect of MMW exposure is temperature increase near the skin surface. Due to the rapid growth in using MMW in common applications including wireless communications systems, automobile collision avoidance systems, airport security screening, non-lethal crowd control weapons, medical imaging, and detection of vital signs such as respiration and heartbeat rates [1] [2] [3], it is important to understand the thermal responses of humans to MMW irradiation and to evaluate biological safety with respect to thermal hazards.
Considerable work has been done in MMW interactions with the human body [4]. We briefly review a few papers that motivate us for this study. In [5], cutaneous thresholds for thermal pain were measured in 10 human subjects (3 female and 7 male Caucasian volunteers, 31 - 70 years old with an average age of 43.7, military or DoD civilians or contractors). Each subject was tested with 3-second exposures to 94 GHz electromagnetic wave of intensity up to 1.8 W/cm2. During each exposure, the temperature increase at the skin’s surface was measured by infrared thermography. The mean baseline temperature of the skin was 34˚C. The irradiated area of the skin has a diameter of 4 cm. The threshold for pricking pain was 43.9˚C (at skin surface). The measured surface temperature was in good agreement with a simple one-dimensional thermal model that accounted for heat conduction and for the penetration depth of the electromagnetic energy into tissue. One important observation in [5] was that the skin surface temperature increased roughly by 10˚C after a 3-second exposure to 1.8 W/cm2 at 94 GHz.
Heating of tissues by electromagnetic waves has also been studied in [6] using Pennes’ bioheat equation, which includes the effect of the blood convection in dissipating the heat. The model was used to estimate the threshold for perception of pain as a function of frequency and exposure duration in the case of plane-wave irradiation. The numerical results in [6] agree well with the experimental thresholds for warmth perception evoked by electromagnetic waves of 2.45 - 94 GHz applied to the back of the test subject for 10-second intervals.
In [7] [8], a one-dimensional multi-layer tissue model was used and solved with the finite difference method to predict temperature variations in the skin exposed to electromagnetic waves. This approach allows estimation of temperature distribution and prediction of burn injury in different layers of the skin depending on blood perfusion rate, thermal conductivity, power density, and exposure time. Even though the numerical simulations were focused on electromagnetic waves with frequencies of 10 GHz and below, this multi-layer model can be extended directly to MMW frequencies. These studies concluded that the rate of skin surface temperature increase in humans in response to brief, high-power MMW exposures can be mathematically modeled using the one-dimensional thermal conduction model.
In [9], a spherical heterogeneous model was developed to simulate the thermal effects (surface and subsurface) on a primate (monkey) head exposed to far-field radiation at 100 GHz. It was found that temperature (both surface and subsurface) increases as the energy level increases, whereas high-power millimeter-waves (HPMs) with power densities in the range of 1.0 to 3.0 W/cm2 for 3 seconds have a higher peak temperature than low-power millimeter-waves (LPMs) in the range of 0.1 to 0.3 W/cm2 for 30 seconds. The surface temperature increase is generally linear with applied energy density for HPMs except under combined conditions of high blood-flow rate and high-energy density. In contrast, with LPMs, the surface temperatures do not behave linearly with respect to incident energy. The simulations also showed that the subsurface (i.e., mid-scalp and mid-skull) temperature increases are substantially damped compared to the surface (i.e., scalp) temperature.
Far-field exposure of the human face to a linearly polarized plane wave at frequencies from 6 to 100 GHz and with exposure durations of 100 milliseconds to 10 seconds was modeled in [10]. The Maxwell equations were solved using a finite-difference time-domain solver. The Pennes’ bioheat transfer equation extended with a term representing the electromagnetic power absorption was used to model body temperature and it was numerically solved. The electromagnetic and thermal simulations revealed highly non-uniform frequency-dependent patterns of temperature rise.
According to a review published in 2016 [11], there are very limited data in the literature related to skin temperature rises or thermal sensation thresholds in humans exposed to MMWs. Most data involves brief exposures to MMWs around 94 GHz [12]. For example, experiments with 13 male adults were conducted in San Antonio, TX to quantify the thermal and behavioral effects of exposure to 30 kW and 95 GHz MMW [13]. The experimental results indicated that the power density necessary to achieve pain intolearability in 90% of the human subject population is 3.03 W/cm2 when the duration of the exposures was fixed at 3 seconds. The effects of variable spot size (beam diameter) on human exposure to 95 GHz MMW were investigated in [14] with a small number of volunteers. The experiments confirmed that repel times of stationary subjects decreased with increasing beam size, although the strength of this relationship varied with power density.
In this paper, we study the mathematical framework for human subjects’ behavioral responses when exposed to millimeter wave radiation. The electromagnetic energy absorbed in the skin increases the skin temperature via dielectric heating. High temperature activates the heat-sensitive nociceptors which produce a stimulus that is sent to the Central Nervous System (CNS) [15]. When the stimulus is sufficiently strong, the withdrawal reflex is initiated and the subject moves away from the exposure. The withdrawal reflex is also called nociceptive flexion reflex and is a spinal reflex intended to protect the body from noxious stimulations [16]. In the ADT CHEETEH-E model [17] recently developed at the Institute for Defense Analyses, the process from the power emitted at the radiation antenna to the subject’s behavioral response is divided into multiple sub-steps, and model components were proposed to describe individual sub-steps [17]. In this study, we follow these model components as general guidelines and use only the physical principles of these model components. We construct a concise dose-response relation for predicting the occurrence of withdrawal reflex based on the spatial temperature profile. The resulting concise model is independent of the specific function forms and parameters used in the sub-steps of ADT CHEETEH-E [17]. In our formulation, the dose quantity is defined as the volume of activated region where the temperature is above the activation temperature of nociceptors. The dose-response model for withdrawal reflex is specified by only two parameters: the activation temperature of nociceptors (
) and the critical threshold on the dose quantity (
). When the spatial temperature profile at reflex is measurable, the two model parameters
and
can be determined from test data. The inference formulation for calculating
and
is based solely on the measured temperature profiles. It does not depend on any symmetry of temperature profile or electromagnetic heating or heat conduction. It does not require any input parameter.
The dose-response model maps a given spatial temperature profile to the binary outcome of subject’s reflex response. We connect it to a time evolution model governing the temperature increase for electromagnetic heating in the skin. The result is a composite model that takes as input the electromagnetic beam deposited on the skin, which is characterized by the beam spot area and the power density. For the temperature evolution, we first consider the simple case of uniform temperature over beam cross-section with no heat conduction (which we shall call idealized case A). The exact solution of temperature is proportional to the time and proportional to the applied power density. Its spatial shape is determined by that of the electromagnetic heating. In order to assess the validity of no-conduction approximation, we consider the case of uniform temperature over the beam cross-section with heat conduction in the depth direction (which we shall call idealized case B). To pinpoint the effects of individual parameters and to facilitate the exact solution, we carry out non-dimensionalization. The temperature solution of the non-dimensional system is the product of the applied power density and a standardized parameter-free function, which we shall call the normalized temperature. The normalized temperature as a function of non-dimensional time and depth has no dependence on the power density or any other parameters. The effects of physical parameters are contained in the non-dimensional variables and in the non-dimensional power density (the multiplier coefficient). Comparing the solutions, respectively, in the presence and in the absence of heat conduction, we find that the no-conduction approximation is appropriate only in the region away from the skin surface and only over a short time. With the analytical solution, we explore the theoretical behaviors of the system and discuss the issues listed below.
· We derive the asymptotic expansion of reflex time at large beam spot area, and compare the result with that in the case of no heat conduction.
· We investigate the biological latency (time delay) in the observed withdrawal reflex. We formulate an algorithm for determining the time delay in the observed withdrawal reflex. The algorithm is based solely on three data points of observed reflex time vs. applied power density. The algorithm is parameter-free, and thus, is operationally applicable in all situations.
· We carry out asymptotic analysis on the normalized temperature respectively for small time and for large time. Building on the asymptotic behaviors of normalized temperature, we construct asymptotic approximations of the reflex time respectively for large and for small applied power density.
· Using the asymptotic results obtained, we examine the energy consumption by the time of reflex, as a function of applied power density. We find that the energy consumption attains a minimum at a moderately large value of applied power density.
· We examine the spatial temperature profile at reflex and demonstrate that it converges to the no-conduction solution at large power density.
· We study how to select test conditions for determining model parameters
from the measured temperature profiles at reflex. Each data set yields only one constraint on
. To determine both
and
simultaneously, we need to obtain distinct constraints on
, which is achieved by carrying out tests both with large beam spot area and with moderate beam spot area.
Finally, we do a case study of Gaussian beams using numerical simulations. We revisit the theoretically predicted behaviors of the system derived in the idealized case B (uniform temperature over beam cross-section). For Gaussian beams (which do not satisfy the assumptions of case B), 1) we evaluate the performance of the algorithm for estimating the biological latency from a sequence of observed reflex times; 2) we examine the existence of energy consumption minimum with respect to the applied power density; and 3) we test the strategy of selecting optimal test conditions for determining model parameters
and
.
2. Review of ADT CHEETEH-E Model [17]
The ADT CHEETEH-E model was proposed in [17] for predicting heat-induced withdrawal reflex of a subject exposed to an electromagnetic beam. The computational framework starts at the radiation antenna which sends the millimeter wave toward the skin surface of a subject, located at a certain distance away. Let N be the number of radiators in the antenna and
be the power output of the i-th radiator. The power output of the antenna is described by the vector
. We review the formulation components used in [17] for modeling sub-steps in the process from the electromagnetic power output of the antenna eventually to the subject’s behavioral response.
1) Electric field near the skin of the subject
where:
-
is the position vector of a point on the skin surface of the subject;
-
is the position vector of the i-th radiator of the antenna;
-
and
are respectively the magnitude and the unit direction of vector
;
-
is the atmospheric attenuation coefficient;
-
is the wave number of the electromagnetic wave;
is the wave length; and
.
2) Power incident per area on the skin
3) Power deposited per area on the skin
4) Power absorbed per volume into the skin
where
is the coordinate of depth from the skin surface and
is the characteristic depth that the millimeter wave penetrates into the skin. In the formulation here
is a vector in
, restricted to the 2-D skin surface, describing the 2-D coordinates on the skin surface. In a local 3-D coordinate system with the depth direction selected as an axis,
is effectively a vector in
, and mathematically
represents the 3-D coordinates in the skin.
5) Temperature as a function of spatial coordinates and time
The temperature distribution is governed by the heat conduction along the depth direction with a source term of electromagnetic heating.
where
-
is the mass density of the subject’s skin;
-
is the specific heat capacity of the skin and;
- K is the thermal conductivity of the skin.
In the initial boundary value problem above, an insulated boundary condition is imposed at the skin surface (
).
6) Number of heat-sensitive nociceptors activated in a local voxel
Each small voxel either has all its heat-sensitive nociceptors activated or has none of them activated depending on the average temperature.
where
- voxel j is a volume element in the computational discretization;
-
is the volume of voxel j;
-
is the density of heat-sensitive nociceptors in the subject’s skin;
-
is the average temperature of voxel j at time t and;
-
is the activation temperature of heat-sensitive nociceptors.
7) Total number of heat-sensitive nociceptors activated at time t
where M is the number of voxels in the computational discretization.
8) Perceived pain level
9) Motivation-modulated perceived pain level
10) Subject’s behavioral response
3. A Concise Model for the Withdrawal Reflex
This section focuses on the occurrence of withdrawal reflex, observed as the subject moving out of beam in tests. At a given time t, we consider the event that the spatial temperature profile results in withdrawal reflex. In terms of the subject’s behavioral response, this event is simply described by
. To formulate a concise model, we follow the model components proposed in [17] as guidelines. We adopt the same assumption that the perceived pain level at time t is solely determined by the number of activated nociceptors at time t, which in turn is solely determined by the spatial temperature profile at time t. In other words, given the temperature profile at time t, the past history of the temperature profile does not affect the perceived pain level at time t. Our strategy is to use only the principles of these model components, not the specific function forms. The goal is to construct a formulation i) that is broadly applicable without assuming a particular function form for any internal sub-step and ii) that is concise with only a few model parameters. Specifically, we require the model to have 3 design features: [leftmargin = 1.5 cm].
· it maps a given spatial temperature profile to the corresponding binary outcome with regard to the occurrence of withdrawal reflex;
· it is independent of the function forms adopted in [17] and;
· it has only two parameters.
Building upon the model components of [17], we proceed with the analysis steps below.
· Based on the relation between
and
(the motivation-modulated perceived pain level) described in model component 10 above, we write.
·
is a monotonically increasing function of
(the perceived pain level). In model component 9 above, this function is set to:
. Here we write generally
and require only that
be an increasing function. Applying
to
, we write:
·
increases monotonically with
(the total number of nociceptors activated). In model component 8 above,
is set to:
. Again, we write generally
and require only that
be an increasing function. Applying
to
, we write:
· At a given time t,
is determined from the spatial temperature profile
:
where the indicator function
is defined as:
Using this expression of
, we write the event in terms of
:
(1)
Result (1) leads to a deterministic dose-response relation for withdrawal reflex. Given spatial temperature profile
, we select the activated volume as the single metric predictor variable (the dose quantity) for predicting withdrawal reflex.
(2)
Here we use
as a concise notation for spatial temperature profile
. Equation (1) tells us that the critical threshold on dose z for withdrawal reflex is
(3)
The deterministic dose-response model is
(4)
Model (4) is completely specified by 2 parameters:
and
.
· Activation temperature
is used in calculating dose z in (2).
· Threshold
is used in determining the binary outcome corresponding to dose z.
Note that threshold
varies with many internal parameters of ADT CHEETEH-E [17]:
·
in the subject behavioral response function
;
· m and
in the motivation modulated perceived pain level
;
· a, b and c in the perceived pain level
and;
·
in the total number of nociceptors activated
.
In addition, threshold
depends on function forms of
and
. The advantage of model (4) is that the effect of all these model parameters and function forms is captured in a single parameter
. Once the values of
and
are known, dose-response model (4) is completely specified.
4. Inferring Model Parameters from Spatial Temperature Profiles
We study the methodology of determining the two parameters (
and
) in model (4) from test data. We consider the hypothetical situation where the temperature of the skin as a function of the 3-D coordinates and the time is measurable in experiments.
The dose-response model described in (4) is based on the assumption that the occurrence of withdrawal reflex at time
is solely attributed to the spatial temperature profile at
. As a result, in the inference method, only
is relevant for determining
and
. In experimental setup, two quantities are tunable: the power density deposited on the skin surface
and the beam spot area A. When the applied power density is uniform inside a geometric area and zero outside, the beam spot is naturally defined as that area. When the applied power density is a function of the 2-D coordinates on the skin surface:
, the scalar beam spot area A refers to a characteristic area of the beam cross-section. For a Gaussian beam with radius w, the beam spot may refer to the circle of radius w around the beam center, which is the region of
or equivalently the region of . Alternatively, the beam spot area may refer to the peak effective area, which is defined as
. Alternatively, the beam spot area may refer to the peak effective area, which is defined as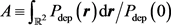 .
.
In test data, information on the unknown parameters 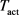 and
and  is contained in the reflex time
is contained in the reflex time 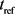 and in the spatial temperature profile at reflex
and in the spatial temperature profile at reflex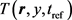 . For a given
. For a given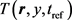 , we can set the activation temperature
, we can set the activation temperature 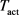 to any reasonable value within the range of
to any reasonable value within the range of . Then, for each value of
. Then, for each value of , the threshold
, the threshold 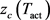 is the activated volume calculated according to
is the activated volume calculated according to .
.
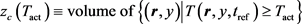 (5)
(5)
Function 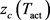 defined in (5) is based on the temperature profile
defined in (5) is based on the temperature profile 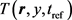 . Given
. Given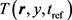 , the pair
, the pair  explains the observed reflex time
explains the observed reflex time 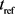 for any value of
for any value of![]() . In other words, one temperature profile
. In other words, one temperature profile ![]() does not provide enough information for determining both
does not provide enough information for determining both ![]() and
and ![]() simultaneously. At a given test condition, the measurements provide only one constraint function
simultaneously. At a given test condition, the measurements provide only one constraint function ![]() on the two unknown parameters. When the test condition
on the two unknown parameters. When the test condition ![]() is varied in experiments, the reflex time
is varied in experiments, the reflex time ![]() and the temperature profile at reflex
and the temperature profile at reflex ![]() will change, and accordingly, the constraint function
will change, and accordingly, the constraint function ![]() may be different. The influence of test condition on the constraint function
may be different. The influence of test condition on the constraint function ![]() offers hope of constructing substantially distinct equations for
offers hope of constructing substantially distinct equations for ![]() from data measured at different test conditions. Once we obtain two different constraint equations for
from data measured at different test conditions. Once we obtain two different constraint equations for![]() , the two unknown parameters are solved simultaneously from a
, the two unknown parameters are solved simultaneously from a ![]() system.
system.
![]() (6)
(6)
Let us summarize and clarify what information regarding model parameters ![]() we can extract from measured temperature profiles and how we extract it.
we can extract from measured temperature profiles and how we extract it.
· At a given test condition![]() , the two unknown parameters
, the two unknown parameters ![]() and
and ![]() are constrained by only one function:
are constrained by only one function:![]() .
.
· As described in (5), constraint function ![]() is completely determined by the measured spatial temperature profile
is completely determined by the measured spatial temperature profile![]() . Function
. Function ![]() is parameter-free.
is parameter-free.
· In the subsequent sections, we will analyze the behaviors of ![]() in certain idealized cases. It is important to point out that the construction of
in certain idealized cases. It is important to point out that the construction of![]() , given in (5), is not dependent on the assumptions of these idealized cases. The assumptions are for the purpose of facilitating the exact solution of temperature evolution.
, given in (5), is not dependent on the assumptions of these idealized cases. The assumptions are for the purpose of facilitating the exact solution of temperature evolution.
· If test data from different test conditions provide two distinct constraint equations, then parameters ![]() can be determined from the
can be determined from the ![]() system (6).
system (6).
In the next section, we will explore theoretically what test conditions are likely to provide substantially distinct constraint equations for![]() . To make it possible to solve the problem analytically, we will introduce assumptions and consider idealized cases in the analysis. The results of the mathematical study on these idealized cases are only intended as guidelines for selecting test conditions that will (in the idealized cases) provide substantially distinct constraint equations for
. To make it possible to solve the problem analytically, we will introduce assumptions and consider idealized cases in the analysis. The results of the mathematical study on these idealized cases are only intended as guidelines for selecting test conditions that will (in the idealized cases) provide substantially distinct constraint equations for![]() . Once the tests are carried out and measurements are collected, the construction of constraint equations
. Once the tests are carried out and measurements are collected, the construction of constraint equations ![]() is based on the real test data using formula (5), which does not depend on any assumption used in the idealized cases. The process of determining
is based on the real test data using formula (5), which does not depend on any assumption used in the idealized cases. The process of determining ![]() is solely based on measured temperature profiles at several test conditions. It does not require any symmetry of temperature or any particular parameter values for the heat absorption/conduction in the skin.
is solely based on measured temperature profiles at several test conditions. It does not require any symmetry of temperature or any particular parameter values for the heat absorption/conduction in the skin.
5. Theoretical Behaviors of the System in the Case of No Heat Conduction
In this section, we study the case of no heat conduction. We examine the behaviors of the temperature distribution, the time until reflex, the latency in withdrawal reflex, and the constraint function on model parameters based on the spatial temperature profile at reflex. To facilitate the analysis in a simple theoretical setting, we first introduce idealized cases.
5.1. Idealized Case U and Case A
Idealized case U is characterized by the two assumptions below:
1) At any given time, the temperature is uniform over the beam cross-section A (i.e., independent of![]() ) and is a decreasing function of depth y.
) and is a decreasing function of depth y.
2) Outside the beam cross-section, the temperature is always below the nociceptor activation temperature (for example, at the normal body temperature).
One particular situation of case U is when the initial temperature of skin is a constant below the activation temperature and the applied power density is uniform over the beam cross-section A and zero outside. Mathematically, idealized case U is characterized by
![]() (7)
(7)
In case U, it is mathematically more convenient to view the constraint function in the form of ![]() with
with ![]() as the independent variable. Recall that the dose z is defined as the volume of the activated region, which in case U is a cylinder with base area A. Dose z has the expression:
as the independent variable. Recall that the dose z is defined as the volume of the activated region, which in case U is a cylinder with base area A. Dose z has the expression:![]() . Given the threshold
. Given the threshold ![]() on activated volume and the beam spot area A, the corresponding activated depth is
on activated volume and the beam spot area A, the corresponding activated depth is![]() . The activation temperature
. The activation temperature![]() , and
, and ![]() are related in the temperature distribution
are related in the temperature distribution ![]()
![]() (8)
(8)
Equation (8) serves various purposes depending on which are known/unknown. On one hand, given the reflex time ![]() and the spatial temperature profile at reflex
and the spatial temperature profile at reflex![]() , (8) is a constraint equation for model parameters
, (8) is a constraint equation for model parameters![]() . On the other hand, given model parameters
. On the other hand, given model parameters![]() , (8) is an equation for the reflex time
, (8) is an equation for the reflex time![]() . We will use this equation to solve for
. We will use this equation to solve for ![]() in case A and case B below, which are special situations of case U. Notice that constraint function
in case A and case B below, which are special situations of case U. Notice that constraint function ![]() given by (8) in case U is simply the temperature profile at reflex, scaled in the depth direction by a factor of 1/A. Based on the mathematical form of (8), intuitively we can change how fast
given by (8) in case U is simply the temperature profile at reflex, scaled in the depth direction by a factor of 1/A. Based on the mathematical form of (8), intuitively we can change how fast ![]() varies with
varies with ![]() by reducing/increasing beam spot area A in experiments.
by reducing/increasing beam spot area A in experiments.
It should be mentioned that case U does not exclude heat conduction in the depth direction. We now add the assumption of no-heat-conduction and introduce case A.
![]() (9)
(9)
Case A satisfies the conditions of case U, and is a special situation of case U.
5.2. Selecting Test Conditions for Determining ![]()
Case A is solved analytically in Appendix A. The temperature distribution and the reflex time are given by (see Equations (65) and (66) of Appendix A).
![]() (10)
(10)
It follows from (8) that the constraint function ![]() has the expression
has the expression
![]() (11)
(11)
Let ![]() denote the true value of
denote the true value of![]() . With this specific notation for the true values, we can use
. With this specific notation for the true values, we can use ![]() to represent the independent variable and
to represent the independent variable and ![]() the dependent variable in constraint function
the dependent variable in constraint function ![]() without confusion.
without confusion.
We like to get rid of ![]() in (11) by using
in (11) by using![]() . In the inference method,
. In the inference method,
we view (11) as a constraint function on ![]() while
while ![]() is known (from data). Alternatively (11) may be viewed as the governing equation for
is known (from data). Alternatively (11) may be viewed as the governing equation for ![]() when
when ![]() and
and ![]() are given. We use (11) to express
are given. We use (11) to express ![]() in terms of
in terms of ![]() and then substitute the expression back into (11) to write constraint function
and then substitute the expression back into (11) to write constraint function ![]() as
as
![]()
We cast the constraint function into the form of ![]() vs.
vs. ![]()
![]() (12)
(12)
Constraint function (12) is specified by two parameters: ![]() and
and![]() . Note that (12) is the constraint function for case A (the case of no heat conduction) and it is independent of the power density
. Note that (12) is the constraint function for case A (the case of no heat conduction) and it is independent of the power density![]() , which specifies how fast the electromagnetic beam heats up the skin. When the effect of heat conduction along the depth direction is included,
, which specifies how fast the electromagnetic beam heats up the skin. When the effect of heat conduction along the depth direction is included, ![]() will affect the steepness of spatial temperature profile at reflex. A smaller power density
will affect the steepness of spatial temperature profile at reflex. A smaller power density ![]() heats up the skin slower and the heat conduction has more time before reflex to smooth out the temperature profile.
heats up the skin slower and the heat conduction has more time before reflex to smooth out the temperature profile.
Figure 1 compares constraint functions constructed from simulated test data
![]()
Figure 1. Constraint functions on ![]() based on simulated data in case A. The intersection of two distinct constraint functions determines the true values
based on simulated data in case A. The intersection of two distinct constraint functions determines the true values![]() .
.
in case A, with two different beam spot areas: ![]() and
and![]() . The well-defined intersection of the two curves gives us the true value
. The well-defined intersection of the two curves gives us the true value ![]() and
and![]() . In simulations, we used
. In simulations, we used![]() . The choice of
. The choice of ![]() does not actually alter the essential shape of constraint functions. If we divide (12) by
does not actually alter the essential shape of constraint functions. If we divide (12) by ![]() and use the scaled temperature as the dependent variable, then (12) is completely specified by
and use the scaled temperature as the dependent variable, then (12) is completely specified by![]() , independent of
, independent of![]() .
.
In summary, in case A, to determine model parameters ![]() and
and![]() , we need to carry out tests with different beam spot areas: one with a moderate value of
, we need to carry out tests with different beam spot areas: one with a moderate value of ![]() to make the constraint function
to make the constraint function ![]() vs.
vs. ![]() slant, the other with a relatively large value of
slant, the other with a relatively large value of ![]() to make
to make ![]() vs.
vs. ![]() flat. Notice that the meanings of phrases “moderate value of
flat. Notice that the meanings of phrases “moderate value of![]() ” and “relatively large value of
” and “relatively large value of![]() ” are not precise since quantity
” are not precise since quantity ![]() is not dimensionless. This issue will be addressed when we discuss non-dimensionalization.
is not dimensionless. This issue will be addressed when we discuss non-dimensionalization.
5.3. Time until Withdrawal Reflex vs. Beam Spot Area
We study how the reflex time ![]() varies with the beam spot area A while the power density
varies with the beam spot area A while the power density ![]() is maintained at a constant level. In case A (the case of no heat conduction), the analytical expression of
is maintained at a constant level. In case A (the case of no heat conduction), the analytical expression of ![]() is given in (10). In expression (10), when the beam spot area
is given in (10). In expression (10), when the beam spot area ![]() is fixed, the reflex time
is fixed, the reflex time ![]() is inversely proportional to the applied power density
is inversely proportional to the applied power density![]() . When
. When ![]() is fixed, as beam spot area A increases,
is fixed, as beam spot area A increases, ![]() decreases. But
decreases. But ![]() is not inversely proportional to A. Eventually
is not inversely proportional to A. Eventually ![]() reaches a constant level above zero for large A. This can be seen in the Taylor expansion of (10) as
reaches a constant level above zero for large A. This can be seen in the Taylor expansion of (10) as![]() .
.
Case A: no heat conduction
![]() (13)
(13)
In all realistic situations, heat conduction is always present. Case A (the case of no heat conduction) corresponds to the situation where the effect of heat conduction is relatively small in comparison with others. In the non-dimensional analysis of the next section, we will see that the effect of heat conduction is negligible only in a region away from the skin surface and only over a short time. Even during a short time, near skin surface, the heat conduction may still be significant or even dominant in the temperature evolution. Expression (10) for ![]() is derived based on the no-conduction approximation of the temperature at depth
is derived based on the no-conduction approximation of the temperature at depth![]() . For large A, depth
. For large A, depth ![]() is close to the skin surface. As a result, expression (10) for
is close to the skin surface. As a result, expression (10) for ![]() eventually becomes invalid for large A. Expanding
eventually becomes invalid for large A. Expanding ![]() vs. A with the effect of heat conduction will be carried out after the non-dimensionalization analysis. We will see that with the effect of heat conduction, the (1/A) term in expansion (13) is invalid.
vs. A with the effect of heat conduction will be carried out after the non-dimensionalization analysis. We will see that with the effect of heat conduction, the (1/A) term in expansion (13) is invalid.
5.4. Latency in Withdrawal Reflex
We hypothesize that when the number of nociceptors activated reaches a threshold, the stimulus sent to the Central Nervous System (CNS) is strong enough to initiate the withdrawal reflex. However, it takes time for the signal to travel to the CNS, for the CNS to send a signal to muscles, and for muscles to act upon the signal to carry out the withdrawal reflex before the actual withdrawal reflex action (i.e., the subject moving out of the beam) is observed in tests. To facilitate the discussion of biological latency in the observed withdrawal reflex, we first introduce proper mathematical notations for these time instances. Let
· ![]() = time until the activated volume (dose z) reaches threshold
= time until the activated volume (dose z) reaches threshold![]() ;
; ![]() is the time until a stimulus strong enough for initiating withdrawal reflex is generated; we regard
is the time until a stimulus strong enough for initiating withdrawal reflex is generated; we regard ![]() as the true underlying reflex time in the sense that even if the beam power is turned off at that point, withdrawal reflex will still occur;
as the true underlying reflex time in the sense that even if the beam power is turned off at that point, withdrawal reflex will still occur;
· ![]() = time until observed withdrawal reflex;
= time until observed withdrawal reflex; ![]() is the observed reflex time;
is the observed reflex time;
· ![]() = latency (time delay) in the observed withdrawal reflex.
= latency (time delay) in the observed withdrawal reflex.
We assume that the time delay ![]() is an intrinsic property of the test subject, not affected by parameters of the electromagnetic beam, such as power density (
is an intrinsic property of the test subject, not affected by parameters of the electromagnetic beam, such as power density (![]() ) or beam spot area (A). In case A (the case of no heat conduction), the true underlying reflex time
) or beam spot area (A). In case A (the case of no heat conduction), the true underlying reflex time ![]() is given by (10). The observed reflex time
is given by (10). The observed reflex time ![]() has the expression:
has the expression:
![]() (14)
(14)
The plot of ![]() vs
vs ![]() is a straight line. The vertical intercept of the plot gives us
is a straight line. The vertical intercept of the plot gives us![]() , which can be estimated from measured values of
, which can be estimated from measured values of ![]() at
at ![]() and
and![]() .
.
Case A: no heat conduction
![]() . (15)
. (15)
6. Non-Dimensionalization and Solution of Heat Conduction in the Depth Direction
We study the effect of heat conduction along the depth direction of the skin (the y-direction of the coordinate system). We first introduce case B which has all assumptions of case A except that it includes the effect of heat conduction in the depth direction with uniform thermal conductivity:![]() .
.
![]() (16)
(16)
In case B, the temperature distribution is governed by
![]() (17)
(17)
6.1. Non-Dimensionalization
We introduce a temperature scale![]() , the characteristic difference between the initial temperature
, the characteristic difference between the initial temperature ![]() and the nociceptor activation temperature
and the nociceptor activation temperature![]() . Note that
. Note that ![]() serves only as the temperature scale for non-dimensionalization.
serves only as the temperature scale for non-dimensionalization. ![]() does not need to be the exact difference between
does not need to be the exact difference between ![]() and
and![]() . We look at the physical dimensions of various quantities:
. We look at the physical dimensions of various quantities:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We introduce length scale and time scale
![]()
Here ![]() is the depth at which the beam decays by a factor of
is the depth at which the beam decays by a factor of![]() , and
, and ![]() is the time at which a
is the time at which a ![]() function spreads to a Gaussian distribution of standard deviation
function spreads to a Gaussian distribution of standard deviation![]() . We use these characteristic scales to carry out non-dimensionalization.
. We use these characteristic scales to carry out non-dimensionalization.
Non-dimensional depth and time:
![]()
Non-dimensional temperature as a function of![]() :
:
![]()
Non-dimensional reflex time:
![]()
Non-dimensional power density deposited on skin surface:
![]()
Non-dimensional beam spot area:
![]()
Non-dimensional activation temperature:
![]()
The governing equation for ![]() follows from Equation (17).
follows from Equation (17).
![]() (18)
(18)
The non-dimensional temperature distribution offers two mathematical advantages.
· For![]() , both the initial and the boundary conditions are homogeneous.
, both the initial and the boundary conditions are homogeneous.
· ![]() is proportional to
is proportional to![]() . Function
. Function ![]() is parameter-free. The effects of all other parameters are contained in the non-dimensional variables.
is parameter-free. The effects of all other parameters are contained in the non-dimensional variables.
We define the normalized non-dimensional temperature
![]() (19)
(19)
Here we have denoted ![]() concisely as
concisely as![]() . Function
. Function ![]() is governed by
is governed by
![]() (20)
(20)
Notice that the normalized Equation (20) is parameter-free.
6.2. Analytical Solution
To solve problem (20), we view the forcing term as the time integral of impulse forcing. Let ![]() denote the solution of a unit impulse forcing at
denote the solution of a unit impulse forcing at![]() , which is governed by
, which is governed by
![]() (21)
(21)
In Appendix B, we derive that ![]() has the expression
has the expression
![]()
where ![]() is the complementary error function defined as
is the complementary error function defined as
![]()
We integrate ![]() with respect to s to superpose the effect of forcing in
with respect to s to superpose the effect of forcing in![]() . The solution of problem (20) is given by
. The solution of problem (20) is given by
![]()
Function ![]() satisfies:
satisfies:
(i) At each fixed y, ![]() is an increasing function of t.
is an increasing function of t.
(ii) At each fixed t, ![]() is a decreasing function of y.
is a decreasing function of y.
(iii) At a fixed y, for small t, ![]() increases with t more than linearly; for large t, the increase is slower than linear.
increases with t more than linearly; for large t, the increase is slower than linear.
The third property of ![]() illustrates the two opposite effects of heat conduction. In the absence of heat conduction, the heating term
illustrates the two opposite effects of heat conduction. In the absence of heat conduction, the heating term ![]() leads to a linearly increasing temperature
leads to a linearly increasing temperature![]() . With heat conduction, at a fixed depth y, function
. With heat conduction, at a fixed depth y, function ![]() starts at
starts at ![]() and increases over short time. As a result,
and increases over short time. As a result, ![]() initially rises faster than
initially rises faster than![]() . Over long time, however, heat conduction eventually pulls
. Over long time, however, heat conduction eventually pulls ![]() back below
back below ![]() and reduces it gradually to zero. Consequently, for large t,
and reduces it gradually to zero. Consequently, for large t, ![]() grows much slower than
grows much slower than ![]() with growth rate decreasing toward zero. We will revisit property (iii) and derive the behaviors of
with growth rate decreasing toward zero. We will revisit property (iii) and derive the behaviors of ![]() respectively for small t and for large t in the asymptotic analysis of the next section.
respectively for small t and for large t in the asymptotic analysis of the next section.
In summary, in case B (the case with heat conduction), ![]() has the expression
has the expression
![]() (22)
(22)
The pre-scaling physical temperature distribution ![]() is
is
![]() (23)
(23)
Equation (23) expresses the physical temperature distribution ![]() as a scaling and shifting of the normalized non-dimensional temperature
as a scaling and shifting of the normalized non-dimensional temperature![]() , which is parameter-free.
, which is parameter-free.
6.3. Effect of Heat Conduction
We investigate the consequence of neglecting heat conduction (i.e., completely turning off the heat conduction in Equation (20)). Specifically, we remove the
![]() term and the insulated boundary condition in (20). The resulting equation is
term and the insulated boundary condition in (20). The resulting equation is
![]() (24)
(24)
which yields the no-conduction approximation of ![]()
![]() (25)
(25)
It is important to clarify the precise difference between Equations (20) and (24). They do not correspond to different regimes of heat conductivity. Rather, they are both obtained in non-dimensionalization using exactly the same parameters. The only difference is that at the end, in Equation (24) we discard the terms involving heat conduction.
To assess the validity of neglecting heat conduction, we compare ![]() with
with ![]() in Figure 2 at several time instances. Here y and t are the non-dimensional depth and time. When t is small and y is away from 0,
in Figure 2 at several time instances. Here y and t are the non-dimensional depth and time. When t is small and y is away from 0, ![]() , provides a good approximation to
, provides a good approximation to![]() .
.
We examine the relative error in approximating ![]() with
with![]() .
.
![]() (26)
(26)
Figure 3 plots contour lines of relative error ![]() in percentage. Again, here y and t are the non-dimensional depth and time. The results illustrate regions where the relative error is bounded by the specified values.
in percentage. Again, here y and t are the non-dimensional depth and time. The results illustrate regions where the relative error is bounded by the specified values.
For the physical temperature distribution, the no-conduction approximation is
![]() (27)
(27)
![]()
Figure 2. Comparison of ![]() and
and![]() , respectively, the normalized non-dimensional temperatures and its no-conduction approximation.
, respectively, the normalized non-dimensional temperatures and its no-conduction approximation.
![]()
Figure 3. Contour lines of relative error ![]() defined in (26), in percentage.
defined in (26), in percentage.
Approximation (27) is valid when the non-dimensional time ![]() is
is
small and the non-dimensional depth ![]() is away from 0. In the rectangular region of
is away from 0. In the rectangular region of ![]() and
and ![]() (lightly shaded in Figure 3), the relative error in the no-conduction approximation of
(lightly shaded in Figure 3), the relative error in the no-conduction approximation of ![]() is bounded by 5%. No-conduction approximation (27) is valid only at depth away from the skin surface. When depth
is bounded by 5%. No-conduction approximation (27) is valid only at depth away from the skin surface. When depth ![]() is small (near skin surface), we need to restrict
is small (near skin surface), we need to restrict ![]() to a very small range in order to maintain a reasonably low relative error
to a very small range in order to maintain a reasonably low relative error![]() . For example, at depth
. For example, at depth![]() , to make the relative error bounded by 5%, we have to restrict the non-dimensional time to the tiny interval of
, to make the relative error bounded by 5%, we have to restrict the non-dimensional time to the tiny interval of ![]() (darkly shaded rectangle in Figure 3).
(darkly shaded rectangle in Figure 3).
7. Theoretical Behaviors of the System in the Case with Heat Conduction
In this section, we study the behaviors of case B (the case with heat conduction), based on its analytical solution. We examine the reflex time vs. beam spot area, the latency in withdrawal reflex, asymptotics of the normalized temperature for small t and for large t, the energy consumption at small and at large applied power density, the spatial temperature profile at reflex, and constraint functions constructed from spatial temperature profiles.
7.1. Reflex Time vs. Beam Spot Area
In subsection 5.3, we studied the asymptotic behavior of reflex time for large beam spot in case A (the case of no heat conduction). The asymptotic result of ![]() vs A in case A is given in (13). The derivation of (13) is based on the no-conduction approximation at depth
vs A in case A is given in (13). The derivation of (13) is based on the no-conduction approximation at depth ![]() and time
and time![]() . As we discussed in subsection 6.3, the no-conduction approximation is valid only in the region away from the skin surface and only over short time. When we increase the beam spot area A, the depth
. As we discussed in subsection 6.3, the no-conduction approximation is valid only in the region away from the skin surface and only over short time. When we increase the beam spot area A, the depth ![]() converges to zero and the time
converges to zero and the time ![]() decreases to a positive value above zero. For large A, the combination of depth
decreases to a positive value above zero. For large A, the combination of depth ![]() and time
and time ![]() leads to a large relative error in the no-conduction approximation. Thus, when the beam spot is large, the no-conduction approximation is no longer valid. We now analyze the asymptotic behavior of
leads to a large relative error in the no-conduction approximation. Thus, when the beam spot is large, the no-conduction approximation is no longer valid. We now analyze the asymptotic behavior of ![]() for large A in the presence of heat conduction (case B).
for large A in the presence of heat conduction (case B).
In case U defined in (7), which includes case B, the governing equation for ![]() is given in (8). Using the exact solution (23) for case B, we write the equation in terms of the normalized temperature distribution
is given in (8). Using the exact solution (23) for case B, we write the equation in terms of the normalized temperature distribution![]() :
:
![]()
which leads to a non-dimensional equation for ![]()
![]() (28)
(28)
where ![]() is the non-dimensional beam spot area and
is the non-dimensional beam spot area and ![]()
the non-dimensional reflex time as defined in subsection 6.1. As the beam spot area ![]() increases, we expect the reflex time
increases, we expect the reflex time ![]() decrease to a positive value above zero. Thus, for
decrease to a positive value above zero. Thus, for![]() , we seek an expansion of the form:
, we seek an expansion of the form:
![]() (29)
(29)
Substituting expansion form (29) into Equation (28) and carrying out the Taylor expansion of ![]() around
around![]() , we get
, we get
![]() (30)
(30)
Based on governing Equation (20) and expression (22) of![]() , we can derive:
, we can derive:
![]() (31)
(31)
![]()
![]()
Using these results in expansion (30), we obtain
![]() (32)
(32)
Matching corresponding terms of ![]() on both sides of (32) yields
on both sides of (32) yields
![]() (33)
(33)
Using expansion (29) and![]() , we write out the expansion of the physical reflex time.
, we write out the expansion of the physical reflex time.
Case B: with heat conduction
![]() (34)
(34)
where ![]() and
and ![]() are solved from (33) and are given by
are solved from (33) and are given by
![]() (35)
(35)
Here ![]() denotes the inverse function of
denotes the inverse function of ![]() defined in (31). We compare (13) and (34). The reflex time in (34) converges rapidly to a positive value above zero as the beam spot area A increases. The convergence of 1/A2 in (34) (the case with heat conduction) is faster than the convergence of 1/A in (13) (the case of no heat conduction).
defined in (31). We compare (13) and (34). The reflex time in (34) converges rapidly to a positive value above zero as the beam spot area A increases. The convergence of 1/A2 in (34) (the case with heat conduction) is faster than the convergence of 1/A in (13) (the case of no heat conduction).
7.2. Latency in Withdrawal Reflex
We study the behavior of biological latency (time delay) ![]() in observed reflex in case B (the case with heat conduction). We investigate the mathematical formulation for determining
in observed reflex in case B (the case with heat conduction). We investigate the mathematical formulation for determining ![]() from test data. While the true reflex time varies with the applied power density
from test data. While the true reflex time varies with the applied power density ![]() and with the beam spot area A, we assume that the time delay in observed reflex is an intrinsic property of the test subject and is independent of
and with the beam spot area A, we assume that the time delay in observed reflex is an intrinsic property of the test subject and is independent of ![]() and A. In experiments, applied power density
and A. In experiments, applied power density ![]() and beam spot area A are adjustable. Our strategy is to determine the time delay
and beam spot area A are adjustable. Our strategy is to determine the time delay ![]() using observed reflex times at a sequence of
using observed reflex times at a sequence of ![]() values.
values.
The observed reflect time is the sum of the true reflex time and the unknown time delay:![]() . As a function of beam spot area A, the true reflex
. As a function of beam spot area A, the true reflex
time ![]() has expansion (34). At large non-dimensional
has expansion (34). At large non-dimensional![]() , the observed reflex time
, the observed reflex time ![]() is approximately
is approximately
![]() (36)
(36)
In the limit of![]() , the observed reflex time
, the observed reflex time ![]() as a function of
as a function of ![]() has the form:
has the form:
![]() (37)
(37)
![]()
In (37), besides the unknown time delay![]() , the two coefficients
, the two coefficients ![]() and
and ![]() are also unknown while
are also unknown while ![]() is specified in experiments. We want to estimate
is specified in experiments. We want to estimate ![]() from measurements of
from measurements of ![]() vs
vs![]() . Notice that the three unknowns
. Notice that the three unknowns ![]() and measurable quantities
and measurable quantities ![]() are constrained by a parameter-free function
are constrained by a parameter-free function ![]() in Equation (37). This mathematical observation suggests an approach for determining
in Equation (37). This mathematical observation suggests an approach for determining![]() :
:
· measure three data points of![]() , and use formulation (37) to construct three constraint equations for
, and use formulation (37) to construct three constraint equations for ![]() based on the three measured data points;
based on the three measured data points;
· then solve for ![]() simultaneously from the system of joint constraints.
simultaneously from the system of joint constraints.
Specifically, we carry out tests at 3 values of![]() :
:
![]()
We examine the difference in the observed reflex time. The difference is independent of![]() .
.
![]() (38)
(38)
![]() (39)
(39)
In (38) and (39), the number of unknowns is reduced to two: ![]() and
and![]() . Next, we get rid of unknown
. Next, we get rid of unknown![]() . For that purpose, we consider quantity
. For that purpose, we consider quantity ![]() defined as
defined as
![]() (40)
(40)
From (38) and (39), it follows that ![]() is a function of
is a function of ![]()
![]() (41)
(41)
where function ![]() is defined in terms of
is defined in terms of ![]() as
as
![]() (42)
(42)
Function ![]() is defined in (31) and is parameter-free. As a result, function
is defined in (31) and is parameter-free. As a result, function ![]() introduced above is also parameter-free. Figure 4 demonstrates that
introduced above is also parameter-free. Figure 4 demonstrates that ![]() is an increasing function. This observation indicates that the inverse function
is an increasing function. This observation indicates that the inverse function ![]() is well defined.
is well defined.
In Appendix C, we derive asymptotics of![]() . The asymptotic results are
. The asymptotic results are
![]() (43)
(43)
These asymptotic results establish analytically the invertibility of function ![]() in the region of small u and in the region of large u. The invertibility of
in the region of small u and in the region of large u. The invertibility of ![]() allows the calculation of
allows the calculation of ![]() in Equation (41), which subsequently leads to the determination of
in Equation (41), which subsequently leads to the determination of![]() .
.
We now describe the method of determining ![]() from data of
from data of ![]() vs
vs![]() . Given three data points of observed reflex time vs. power density:
. Given three data points of observed reflex time vs. power density:![]() ,
, ![]() and
and![]() , we proceed as follows. We first calculate quantity
, we proceed as follows. We first calculate quantity ![]() as described in (40). Then we apply the inverse function
as described in (40). Then we apply the inverse function ![]() to both sides of (41) to find
to both sides of (41) to find![]() . Next we substitute the obtained value of
. Next we substitute the obtained value of ![]() into (38) to calculate
into (38) to calculate![]() . Finally, with the values of
. Finally, with the values of ![]() and
and![]() , we calculate
, we calculate ![]() in (37). Mathematically we write the method as an algorithm:
in (37). Mathematically we write the method as an algorithm:
Case B: with heat conduction
![]()
Figure 4. Graph of function ![]() shows it increases monotonically with u.
shows it increases monotonically with u.
![]() (44)
(44)
The last line of (44) gives the predicted function of observed reflex time vs. applied power density, based on the 3 data points. Algorithm (44) is parameter-free. It calculates the time delay ![]() using only the 3 data points. Even though algorithm (44) is derived based on the theoretical behavior of case B in the limit of large beam spot area, operationally it can be applied in any situation since it does not require any input parameter. In the next section, we will test it in the case of a Gaussian beam where the temperature is not uniform over the beam cross-section and the beam radius is finite.
using only the 3 data points. Even though algorithm (44) is derived based on the theoretical behavior of case B in the limit of large beam spot area, operationally it can be applied in any situation since it does not require any input parameter. In the next section, we will test it in the case of a Gaussian beam where the temperature is not uniform over the beam cross-section and the beam radius is finite.
7.3. Temperature at a Fixed Depth for Small Time and Large Time
In this subsection, we study the time evolution of the normalized non-dimensional temperature ![]() at a fixed y, respectively for small t and for large t. Here the pair
at a fixed y, respectively for small t and for large t. Here the pair ![]() denotes the non-dimensional depth and time.
denotes the non-dimensional depth and time. ![]() is governed by Equation (20). We will see that over short time, the temperature increase caused by the heating term in (20) is augmented by the heat gain via conduction. Over long time, however, the effect of the heating term is very much diminished by the heat loss via conduction.
is governed by Equation (20). We will see that over short time, the temperature increase caused by the heating term in (20) is augmented by the heat gain via conduction. Over long time, however, the effect of the heating term is very much diminished by the heat loss via conduction.
In solution (22), ![]() is an integral of
is an integral of![]() . We first look at the asymptotics of
. We first look at the asymptotics of![]() . At a fixed
. At a fixed![]() , as
, as ![]() we have
we have![]() . Recall two properties of
. Recall two properties of![]() :
:
![]()
![]()
The abbreviation ![]() stands for Transcendentally Small Terms, which converge to zero faster than any powers of z. At a fixed
stands for Transcendentally Small Terms, which converge to zero faster than any powers of z. At a fixed ![]() and small t, we use these two properties to calculate the expansions of
and small t, we use these two properties to calculate the expansions of ![]() and
and ![]() in (22).
in (22).
![]()
![]() (45)
(45)
In the no-conduction approximation given in (25), ![]() is proportional to t for all t. The increase rate of
is proportional to t for all t. The increase rate of ![]() is independent of t. With heat conduction, the solution
is independent of t. With heat conduction, the solution ![]() increases slightly more than linearly with t in (45) for small t.
increases slightly more than linearly with t in (45) for small t.
![]()
The linear portion of the temperature growth at depth y is attributed to the heating at y from the electromagnetic wave penetrating into the skin. The portion above the linear growth is caused by the positive net heat gain via conduction. For a small interval around y, the net heat gain via conduction is positive when the heat in-flow from the upstream is more than the heat out-flow to the downstream. The temperature growth caused by the electromagnetic heating is augmented by the conduction when the net heat gain via conduction is positive. Mathematically, at depth y, the net heat gain via conduction is positive when![]() , which is true for small t. We will show below that for large t, however, the net heat gain via conduction is negative. As a result, the temperature increase caused by electromagnetic heating is diminished by heat conduction, and the realized temperature increase for large t is much smaller than the linear growth.
, which is true for small t. We will show below that for large t, however, the net heat gain via conduction is negative. As a result, the temperature increase caused by electromagnetic heating is diminished by heat conduction, and the realized temperature increase for large t is much smaller than the linear growth.
To expand ![]() for large t, we write it in terms of the scaled complementary error function
for large t, we write it in terms of the scaled complementary error function![]() .
.
![]()
We use the expansion of ![]() given in (68) of Appendix C.
given in (68) of Appendix C.
![]() (46)
(46)
Integrating the expansion of ![]() with respect to t, we obtain
with respect to t, we obtain
![]() (47)
(47)
The constant term ![]() is undetermined in the integration. In Appendix D, we derive
is undetermined in the integration. In Appendix D, we derive![]() . For large t,
. For large t, ![]() increases like
increases like![]() , much slower than the linear growth in the no-conduction approximation
, much slower than the linear growth in the no-conduction approximation![]() . The effect of the heating term in (20) is very much neutralized by the net heat loss at y via conduction. This slow temperature increase at large t is in sharp contrast with the situation for small t where the effect of the heating term is augmented by the net heat gain via conduction. Of course, heat is conserved in the conduction. The net heat loss at depth
. The effect of the heating term in (20) is very much neutralized by the net heat loss at y via conduction. This slow temperature increase at large t is in sharp contrast with the situation for small t where the effect of the heating term is augmented by the net heat gain via conduction. Of course, heat is conserved in the conduction. The net heat loss at depth ![]() contributes to a potential net heat gain somewhere downstream (at depth
contributes to a potential net heat gain somewhere downstream (at depth![]() ). Expansions (46)
). Expansions (46)
and (47) are based on![]() . The qualification of “large t’’ depends on the value of y. At any fixed t (no matter how large it is), when y is large enough, eventually
. The qualification of “large t’’ depends on the value of y. At any fixed t (no matter how large it is), when y is large enough, eventually ![]() is negative, and expansions (46) and (47)
is negative, and expansions (46) and (47)
are invalid. In the regime of fixed t and large y, the net heat gain at y via conduction is positive. Expansions (46) and (47), however, tell us the behavior in a different regime: at a fixed![]() , when t is large enough, the electromagnetic heating is diminished by the net heat loss via conduction and it produces a much slower temperature growth proportional to
, when t is large enough, the electromagnetic heating is diminished by the net heat loss via conduction and it produces a much slower temperature growth proportional to ![]() instead of t.
instead of t.
We compare the normalized temperature![]() , its asymptotics for small t and for large t, and the no-conduction approximation
, its asymptotics for small t and for large t, and the no-conduction approximation![]() . We like to compare them in their relative differences over a wide range of time t. Given that
. We like to compare them in their relative differences over a wide range of time t. Given that ![]() is proportional to t, we scale everything by 1/t to facilitate the comparison.
is proportional to t, we scale everything by 1/t to facilitate the comparison. ![]() has the physical meaning of the average rate of temperature increase in
has the physical meaning of the average rate of temperature increase in![]() . Figure 5 shows the scaled exact solution
. Figure 5 shows the scaled exact solution![]() , its asymptotic approximations (45) for small t and (47) and for large t, and the scaled no-conduction approximation
, its asymptotic approximations (45) for small t and (47) and for large t, and the scaled no-conduction approximation![]() .
.
We look into the net heat gain/loss due to conduction, for small t and for large t. Differentiating (45) and (47) twice with respect to y, we have
![]() (48)
(48)
The results in (48) are valid only when (45) and (47) are valid, respectively, in the regimes of small t and large t. This is particularly evident in line 2 of (48), which suggests that at fixed depth y, the regime of large t has to satisfy![]() . Since there is no heat in-flow at depth 0 (skin surface), the conduction always leads to an overall heat loss for the interval
. Since there is no heat in-flow at depth 0 (skin surface), the conduction always leads to an overall heat loss for the interval![]() . The local net heat loss is initially confined to near 0 and gradually propagates to the entire interval. For large y, it takes long time for the local net heat loss to reach depth y. It takes even longer time for the net heat loss to offset the previously accumulated heat gain at y and then to substantially neutralize the electromagnetic heating.
. The local net heat loss is initially confined to near 0 and gradually propagates to the entire interval. For large y, it takes long time for the local net heat loss to reach depth y. It takes even longer time for the net heat loss to offset the previously accumulated heat gain at y and then to substantially neutralize the electromagnetic heating.
7.4. Reflex Times at Large and at Small Applied Power Densities
In case B, the temperature is uniform over the beam cross section and the activated region is a cylinder. Given the beam spot area A and the threshold ![]() for activated volume, withdrawal reflex occurs when the temperature at depth
for activated volume, withdrawal reflex occurs when the temperature at depth ![]() reaches the activation temperature
reaches the activation temperature![]() . In this subsection, we use the asymptotics of temperature for small time and for large time (obtained in subsection 7.3) to study the reflex time at large and at small applied power densities. We also compare the results with the no-conduction approximation of the reflex time given in (10), which is inversely proportional to the applied power density.
. In this subsection, we use the asymptotics of temperature for small time and for large time (obtained in subsection 7.3) to study the reflex time at large and at small applied power densities. We also compare the results with the no-conduction approximation of the reflex time given in (10), which is inversely proportional to the applied power density.
In case B, the reflex time ![]() satisfies equation
satisfies equation![]() , as described in (8). The non-dimensional version of the equation is given in (28). For our discussion here, we write the left side of (28) in terms of
, as described in (8). The non-dimensional version of the equation is given in (28). For our discussion here, we write the left side of (28) in terms of ![]() and
and![]() .
.
![]() (49)
(49)
where ![]() is the parameter-free normalized non-dimensional temperature defined in (22). We consider the function of
is the parameter-free normalized non-dimensional temperature defined in (22). We consider the function of ![]() vs
vs ![]() and denote it concisely as
and denote it concisely as![]() .
.
The no-conduction version of Equation (49) is obtained by replacing ![]() with its no-conduction approximation
with its no-conduction approximation![]() . The solution of the no-conduction version of (49) gives the no-conduction approximation of
. The solution of the no-conduction version of (49) gives the no-conduction approximation of ![]()
Case A: no heat conduction
![]() (50)
(50)
For large![]() , we expect small
, we expect small![]() , we use the asymptotic for small t given in (45) to approximate
, we use the asymptotic for small t given in (45) to approximate![]() , and we write Equation (49) approximately as
, and we write Equation (49) approximately as
![]()
which yields
![]() (51)
(51)
Result (51) indicates that heat conduction reduces the reflex time when the applied power density is large. This corresponds to the asymptotic result in subsection 7.3 that at a fixed depth and over short time, heat conduction enhances the temperature increase of electromagnetic heating. We measure the relative reduction in reflex time by
![]()
The relative reduction in reflex time actually increases slightly when the applied power density is slightly decreased as long as it is still in the regime of large power density so that the small time approximation (45) is valid.
For small![]() , we expect large
, we expect large![]() , we use asymptotic for large t given in (47) to approximate
, we use asymptotic for large t given in (47) to approximate![]() , and we write Equation (49) approximately as
, and we write Equation (49) approximately as
![]()
which becomes a quadratic equation for ![]() and gives the solution
and gives the solution
![]() (52)
(52)
![]()
The second solution of the quadratic equation satisfies![]() , which is unreasonable. The expansion of (52) as a power series of
, which is unreasonable. The expansion of (52) as a power series of ![]() is
is
![]() (53)
(53)
![]()
Result (53) indicates that for small applied power density![]() , the reflex time
, the reflex time ![]() increases enormously, proportional to
increases enormously, proportional to ![]() instead of proportional to
instead of proportional to![]() . This corresponds to the asymptotic result in subsection 7.3 that at a fixed depth and over long time, heat conduction results in local net heat loss and significantly diminishes the temperature increase of electromagnetic heating.
. This corresponds to the asymptotic result in subsection 7.3 that at a fixed depth and over long time, heat conduction results in local net heat loss and significantly diminishes the temperature increase of electromagnetic heating.
We compare reflex times![]() , the two asymptotics and
, the two asymptotics and![]() . As
. As ![]() increases,
increases, ![]() varies extensively from being extremely large at small
varies extensively from being extremely large at small ![]() to being near zero at large
to being near zero at large![]() . To examine the relative differences over a wide range of
. To examine the relative differences over a wide range of![]() , we scale everything by
, we scale everything by ![]() to reduce their variations with
to reduce their variations with![]() . In particular, after scaling,
. In particular, after scaling, ![]() is independent of
is independent of![]() . Physically,
. Physically, ![]() has the meaning of energy deposited per area on skin by the time of reflex. When the beam spot area is fixed,
has the meaning of energy deposited per area on skin by the time of reflex. When the beam spot area is fixed, ![]() can be used as a measure of energy consumption by the time of reflex. Figure 6 compares the exact solution
can be used as a measure of energy consumption by the time of reflex. Figure 6 compares the exact solution![]() , its asymptotic approximations (51) for large
, its asymptotic approximations (51) for large ![]() and (52) and for small
and (52) and for small![]() , and the no-conduction approximation
, and the no-conduction approximation![]() .
.
In Figure 6, we make an important observation that the energy consumption has a minimum with respect to applied power density. We now demonstrate the minimum analytically. Based on asymptotics (51) and (53), ![]() has the expansions below, respectively, for small
has the expansions below, respectively, for small ![]() and for large
and for large ![]()
![]() (54)
(54)
For large![]() ,
, ![]() approaches its no-conduction approximation
approaches its no-conduction approximation ![]() from below; for small
from below; for small![]() ,
, ![]() grows unbounded. The minimum of
grows unbounded. The minimum of ![]() is attained in between when
is attained in between when ![]() is moderately large. In general, the range of moderately large
is moderately large. In general, the range of moderately large ![]() is also a good compromise between inducing withdrawal reflex quickly and preventing burn injury of accidental over-heating. For large
is also a good compromise between inducing withdrawal reflex quickly and preventing burn injury of accidental over-heating. For large![]() , burn injury may occur even when the power is turned off shortly after the internal initiation of withdrawal reflex.
, burn injury may occur even when the power is turned off shortly after the internal initiation of withdrawal reflex.
7.5. Spatial Temperature Profile at Reflex
We examine the temperature profile at reflex and how it varies as the applied power density increases from small to large. We compare it with the no-conduction approximation, which is independent of the applied power density.
We follow the equation and notation for the reflex time used in subsection 7.4. At reflex, the non-dimensional temperature has the expression
![]() (55)
(55)
The no-conduction approximation of ![]() is
is![]() , which has separable dependence on t and y. The no-conduction approximation of (55) is
, which has separable dependence on t and y. The no-conduction approximation of (55) is
![]()
which is independent of the applied power density![]() . In the presence of heat conduction, the normalized temperature
. In the presence of heat conduction, the normalized temperature ![]() has non-separable dependence on t and y. Consequently,
has non-separable dependence on t and y. Consequently, ![]() in (55) varies with
in (55) varies with![]() . Figure 7 compares
. Figure 7 compares ![]() for several values of
for several values of ![]() and its no-conduction approximation. As
and its no-conduction approximation. As ![]() increases, the reflex time decreases to zero, and the heat conduction has little time to take its effect. Figure 7 demonstrates that at a fixed depth
increases, the reflex time decreases to zero, and the heat conduction has little time to take its effect. Figure 7 demonstrates that at a fixed depth![]() , as
, as ![]() increases the temperature at reflex converges to that in the case of no heat conduction. Therefore, at any fixed depth away from the skin surface, the effect of heat conduction is eventually negligible when the applied power density is large enough.
increases the temperature at reflex converges to that in the case of no heat conduction. Therefore, at any fixed depth away from the skin surface, the effect of heat conduction is eventually negligible when the applied power density is large enough.
7.6. Selecting Test Conditions for Determining ![]()
The situation of inferring parameters ![]() from temperature profiles at
from temperature profiles at ![]() is similar to that in the case of no heat conduction. Once the latency
is similar to that in the case of no heat conduction. Once the latency ![]() is determined, the true reflex time is calculated from the observed reflex time:
is determined, the true reflex time is calculated from the observed reflex time:![]() . Given the temperature profile at reflex
. Given the temperature profile at reflex ![]() at one test condition, the activation temperature
at one test condition, the activation temperature ![]() can be set to any value in the range of
can be set to any value in the range of![]() . At each value of
. At each value of![]() , the corresponding threshold
, the corresponding threshold ![]() is calculated as the activated volume at reflex according to formula (5). When restricted to data at one test condition,
is calculated as the activated volume at reflex according to formula (5). When restricted to data at one test condition, ![]() provides only one constraint on
provides only one constraint on![]() ; it does not allow us to determine
; it does not allow us to determine ![]() and
and ![]() simultaneously.
simultaneously.
As we discussed in section 4, constraint function ![]() is calculated
is calculated
directly from the measured temperature profile at reflex![]() . It does not require any model parameter, such as
. It does not require any model parameter, such as![]() , K, or
, K, or![]() . We explore how to obtain substantially distinct constraint equations for
. We explore how to obtain substantially distinct constraint equations for ![]() by carrying out tests at different conditions. In case U (which includes both case A and case B), the activated region is a cylinder with the beam cross section as the base. Given the beam spot area A, the activated volume is completely specified by the activated depth. At reflex, the activated volume is
by carrying out tests at different conditions. In case U (which includes both case A and case B), the activated region is a cylinder with the beam cross section as the base. Given the beam spot area A, the activated volume is completely specified by the activated depth. At reflex, the activated volume is ![]() and the activated depth is
and the activated depth is![]() . In case B, the temperature has the analytical solution given in (22) and (23). When examining the constraint on
. In case B, the temperature has the analytical solution given in (22) and (23). When examining the constraint on ![]() using the analytical solution, it is more convenient to view
using the analytical solution, it is more convenient to view ![]() as a function of
as a function of![]() . For any positive value of
. For any positive value of![]() , the corresponding activation temperature
, the corresponding activation temperature ![]() is given by the temperature at depth
is given by the temperature at depth![]() , which leads to the constraint on
, which leads to the constraint on ![]() described in Equation (8).
described in Equation (8).
The non-dimensional version of (8) is Equation (28). Recall that (28) was derived as the governing equation for the reflex time ![]() when other parameters including
when other parameters including ![]() and
and ![]() are known and fixed. As an equation for
are known and fixed. As an equation for![]() , the meaning of (28) is clear. In the situation of inferring
, the meaning of (28) is clear. In the situation of inferring![]() , reflex time
, reflex time ![]() is known (from data) and we view (28) as a constraint equation on
is known (from data) and we view (28) as a constraint equation on![]() , with
, with ![]() as the independent variable and
as the independent variable and ![]() the dependent variable. In this view, we need to be careful about the precise meaning of various terms in (28).
the dependent variable. In this view, we need to be careful about the precise meaning of various terms in (28).
In particular, the non-dimensional beam spot area ![]() varies with
varies with
independent variable![]() , and thus is no longer a constant. To pinpoint the influence of independent variable
, and thus is no longer a constant. To pinpoint the influence of independent variable ![]() on various terms in (28), we use
on various terms in (28), we use ![]() to denote the true value of
to denote the true value of![]() , and introduce quantities below based on true values
, and introduce quantities below based on true values![]() .
.
![]()
For simplicity and clarity, we use ![]() to denote
to denote ![]() and write
and write ![]() as
as
![]()
With the proper notations clarified above, we write constraint (28) as
![]() (56)
(56)
The true value ![]() satisfies constraint (56). Subtracting the (56) evaluated at
satisfies constraint (56). Subtracting the (56) evaluated at ![]() from the general (56), we write the constraint as
from the general (56), we write the constraint as
![]() (57)
(57)
(57) is a constraint function in the form of ![]() vs
vs ![]() and has three parameters:
and has three parameters:![]() ,
, ![]() and
and![]() . The non-dimensional reflex time
. The non-dimensional reflex time ![]() satisfies Equation (56) at
satisfies Equation (56) at![]() :
:
![]() (58)
(58)
The solution ![]() is a function of
is a function of![]() . It follows that as a function of
. It follows that as a function of ![]() vs
vs![]() , constraint (57) is completely determined once
, constraint (57) is completely determined once ![]() is known.
is known.
We examine constraint (57) in the form of ![]() vs
vs ![]() and explore
and explore
the parameter space of![]() . The purposes of adopting this form are i) to pinpoint the effect of
. The purposes of adopting this form are i) to pinpoint the effect of![]() ; and ii) to focus on the shape of constraint functions relative to their intersection at
; and ii) to focus on the shape of constraint functions relative to their intersection at![]() . As we discussed above, the relative shape is completely determined by
. As we discussed above, the relative shape is completely determined by![]() , independent of other parameters. While this form is the proper mathematical tool for examining the behavior of constraint (57), we do need to point out that in real applications of
, independent of other parameters. While this form is the proper mathematical tool for examining the behavior of constraint (57), we do need to point out that in real applications of
inferring ![]() from test data, the form of
from test data, the form of ![]() vs
vs ![]() is not
is not
operationally realistic since ![]() and
and ![]() are unknown to start with. In real applications, we simply calculate constraint function
are unknown to start with. In real applications, we simply calculate constraint function ![]() from test data using (5), and then find
from test data using (5), and then find ![]() at the intersection of two constraint curves.
at the intersection of two constraint curves.
Figure 8 compares constraint (57) in the form of ![]() vs
vs ![]() at several test conditions. A combination of large beam spot
at several test conditions. A combination of large beam spot ![]() and small power
and small power
density ![]() makes the constraint function flat while a combination of small
makes the constraint function flat while a combination of small ![]() and large
and large ![]() makes it slate. Once we obtain two distinct constraints from different test conditions, the well-defined intersection of the two curves gives us the values of
makes it slate. Once we obtain two distinct constraints from different test conditions, the well-defined intersection of the two curves gives us the values of ![]() and
and![]() .
.
In summary, to reliably determine model parameters ![]() and
and![]() , we need to carry out tests with significantly different combinations of
, we need to carry out tests with significantly different combinations of![]() : one with moderate
: one with moderate ![]() and large
and large![]() , the other with large
, the other with large ![]() and moderate
and moderate![]() .
.
8. The Case of a Gaussian Beam with Heat Conduction
We consider a Gaussian beam with power density
![]() (59)
(59)
where ![]() is the power density at the beam center (
is the power density at the beam center (![]() ) and w is the beam radius, which is twice the standard deviation of the Gaussian distribution. At each value of
) and w is the beam radius, which is twice the standard deviation of the Gaussian distribution. At each value of![]() , the temperature is governed by the electromagnetic heating and the heat conduction along the y-dimension, independent of the temperature at other values of
, the temperature is governed by the electromagnetic heating and the heat conduction along the y-dimension, independent of the temperature at other values of![]() . The temperature distribution
. The temperature distribution ![]() is obtained by applying exact solution (23) at each
is obtained by applying exact solution (23) at each ![]()
![]() (60)
(60)
where ![]() is the parameter-free normalized non-dimensional temperature defined in (22). The activated volume in spatial temperature profile (60) at a given time t does not have a closed-form expression. We use a numerical integration method to calculate the activated volume at any given time. The reflex time
is the parameter-free normalized non-dimensional temperature defined in (22). The activated volume in spatial temperature profile (60) at a given time t does not have a closed-form expression. We use a numerical integration method to calculate the activated volume at any given time. The reflex time ![]() satisfies
satisfies![]() . We use an iterative non-linear solver to find
. We use an iterative non-linear solver to find![]() . Once
. Once ![]() is known, we calculate
is known, we calculate ![]() using (60). Following this procedure, we generate simulated data and then we use the data to test the theoretical predictions derived in the previous section for case B.
using (60). Following this procedure, we generate simulated data and then we use the data to test the theoretical predictions derived in the previous section for case B.
To facilitate the analysis, we introduce parameters ![]() and
and ![]() as in case B, and write temperature distribution (60) in a non-dimensional form, in terms of
as in case B, and write temperature distribution (60) in a non-dimensional form, in terms of ![]() and
and![]() .
.
![]() (61)
(61)
![]() .
.
8.1. Activated Domain and Reflex Time
First, we discuss how to generate simulated data of reflex time in the case of a Gaussian beam with finite radius. At time t, the activated domain is described by
![]() (62)
(62)
Figure 9 shows an example of activated domain for a Gaussian beam. Since the beam center (![]() ) has the highest intensity, near the beam center the skin receives more electromagnetic energy and the activated domain extends more in the depth direction. Away from the beam center, the beam intensity falls quickly and accordingly the depth of activated domain decreases toward 0. This leads to the bowl-shaped activated domain in Figure 9.
) has the highest intensity, near the beam center the skin receives more electromagnetic energy and the activated domain extends more in the depth direction. Away from the beam center, the beam intensity falls quickly and accordingly the depth of activated domain decreases toward 0. This leads to the bowl-shaped activated domain in Figure 9.
Withdrawal reflex occurs when the volume of the activated domain reaches the critical threshold![]() . The reflex time
. The reflex time ![]() is governed by
is governed by
![]() (63)
(63)
We non-dimensionalize spatial coordinates ![]() and y, respectively with scales w and
and y, respectively with scales w and![]() .
.
![]()
Note that ![]() and y are scaled differently. In coordinates
and y are scaled differently. In coordinates![]() , (63) be-comes
, (63) be-comes
![]() (64)
(64)
Equation (64) for ![]() is completely specified by parameters
is completely specified by parameters![]() ,
, ![]() and
and![]() . Function
. Function ![]() is parameter-free and there is no other parameter. In simulations, we use
is parameter-free and there is no other parameter. In simulations, we use
![]()
With these parameters, we solve for the true reflex time ![]() from (64) as a function of
from (64) as a function of![]() . The observed reflex time is calculated as
. The observed reflex time is calculated as![]() . Figure 10 plots the simulated function of
. Figure 10 plots the simulated function of ![]() vs
vs ![]() for a Gaussian beam. We
for a Gaussian beam. We
![]()
Figure 9. Activated domain in the case of a Gaussian beam. (a) Color map of ![]() with the activated domain marked by dashed curve. (b) 3-D view of the activated domain.
with the activated domain marked by dashed curve. (b) 3-D view of the activated domain.
![]()
Figure 10. Observed reflex time ![]() vs beam center power density
vs beam center power density![]() . Comparison of the simulated function (treated as exact) and the prediction by algorithm (44) based solely on the 3 data points shown above, without using any other information.
. Comparison of the simulated function (treated as exact) and the prediction by algorithm (44) based solely on the 3 data points shown above, without using any other information.
regard the simulated ![]() in Figure 10 as exact since it is numerically accurate to the computer precision.
in Figure 10 as exact since it is numerically accurate to the computer precision.
8.2. Estimating the Latency
We study the methodology for determining the time delay in the observed withdrawal reflex:![]() . The time delay
. The time delay ![]() is an intrinsic property of the test subject, independent of the applied power density
is an intrinsic property of the test subject, independent of the applied power density![]() . We estimate the time delay
. We estimate the time delay ![]() based solely on the measured values of observed reflex time
based solely on the measured values of observed reflex time![]() , without using any model parameters. In tests,
, without using any model parameters. In tests, ![]() is tunable. The general strategy is to measure
is tunable. The general strategy is to measure ![]() at a sequence of
at a sequence of ![]() values, and then use the test data to build multiple joint constraints on
values, and then use the test data to build multiple joint constraints on ![]() and other unknowns. All parameters involved in the constraint formulation are treated as unknown, and all unknowns are solved simultaneously from the system of joint constraints.
and other unknowns. All parameters involved in the constraint formulation are treated as unknown, and all unknowns are solved simultaneously from the system of joint constraints.
In subsection 7.2, a joint constraint was constructed for 3 unknowns:![]() ,
, ![]() and
and![]() . Equation (37) is derived in the idealized situation where.
. Equation (37) is derived in the idealized situation where.
· the applied power density is uniform over the beam cross-section and is zero outside; heat conduction is included in the depth direction (case B);
· the beam spot area is large and approaching infinity (![]() ).
).
Given 3 data points, we applied (37) to construct a constraint at each data point. Then we used the joint system of 3 constraints to derive algorithm (44) for determining![]() . Algorithm (44) is based solely on the 3 data points. It does not require any input parameter. In the idealized situation above,
. Algorithm (44) is based solely on the 3 data points. It does not require any input parameter. In the idealized situation above, ![]() solved from algorithm (44) is exact. In this subsection, we test the performance of algorithm (44) for inferring
solved from algorithm (44) is exact. In this subsection, we test the performance of algorithm (44) for inferring ![]() in the case of a Gaussian beam with a finite beam radius. The purpose is to demonstrate the versatility and accuracy of algorithm (44) when the idealized conditions above are not met. Here we focus on the accuracy of estimating the time delay since
in the case of a Gaussian beam with a finite beam radius. The purpose is to demonstrate the versatility and accuracy of algorithm (44) when the idealized conditions above are not met. Here we focus on the accuracy of estimating the time delay since ![]() is our objective while coefficients
is our objective while coefficients ![]() and
and ![]() are just auxiliary unknowns accompanying
are just auxiliary unknowns accompanying ![]() in algorithm (44).
in algorithm (44).
The simulated curve of ![]() vs
vs ![]() for a Gausian beam is shown in Figure 10. From the simulated curve, function values at
for a Gausian beam is shown in Figure 10. From the simulated curve, function values at ![]() and
and ![]() (with
(with![]() ) are selected as the 3 data points, shown as filled squares in Figure 10. These 3 data points and only these 3 data points are then used in algorithm (44) to estimate
) are selected as the 3 data points, shown as filled squares in Figure 10. These 3 data points and only these 3 data points are then used in algorithm (44) to estimate![]() . A Gaussian beam with finite beam radius does not satisfy the idealized conditions above. Nevertheless, we apply algorithm (44) to the 3 data points in Figure 10 to estimate
. A Gaussian beam with finite beam radius does not satisfy the idealized conditions above. Nevertheless, we apply algorithm (44) to the 3 data points in Figure 10 to estimate![]() . Operationally, algorithm (44) is universally applicable in any situation since it does not require any input parameter.
. Operationally, algorithm (44) is universally applicable in any situation since it does not require any input parameter.
Once we obtain the estimated values![]() , we use them in (44) to predict the observed reflex time as a function of
, we use them in (44) to predict the observed reflex time as a function of![]() .
.
![]()
Figure 10 demonstrates that the predicted function ![]() (dashed blue line) is a very good approximation of the exact function (solid red line). Note that the predicted function is based solely on the 3 data points. No other information is used.
(dashed blue line) is a very good approximation of the exact function (solid red line). Note that the predicted function is based solely on the 3 data points. No other information is used.
8.3. Scaling Properties of the Formulation for Estimating Latency
In addition to its high accuracy for estimating the time delay in situations where the idealized conditions are not met, formulation (44) and the predicted function based on it, have several important properties. We now discuss these properties.
1) The prediction is based solely on the 3 data points. Formulation (44) and the predicted function ![]() are parameter-free. Coefficients
are parameter-free. Coefficients ![]() and
and ![]() are auxiliary unknowns that are solved simultaneously with
are auxiliary unknowns that are solved simultaneously with ![]() in Equation (44).
in Equation (44).
2) The prediction is invariant with respect to a shift in![]() . Quantity
. Quantity ![]() defined in (40) contains differences in observed reflex time among the 3 data points, and thus, is independent of time delay
defined in (40) contains differences in observed reflex time among the 3 data points, and thus, is independent of time delay![]() . It follows that
. It follows that ![]() and
and ![]() calculated in (44) are independent of
calculated in (44) are independent of![]() . If the measured values of
. If the measured values of ![]() at 3 data points are shifted by a constant amount, then the estimated time delay
at 3 data points are shifted by a constant amount, then the estimated time delay ![]() and the predicted function
and the predicted function ![]() are both shifted by the same amount. In other words,
are both shifted by the same amount. In other words, ![]() is invariant with respect to
is invariant with respect to![]() . This can be seen by subtracting
. This can be seen by subtracting ![]() in (44)
in (44)
![]()
In the equation above, all quantities on the right hand side are independent of![]() . Thus, the absolute error
. Thus, the absolute error ![]() is not affected by
is not affected by![]() . The absolute error in
. The absolute error in ![]() reflects the model error that the Gaussian beam does not satisfy the idealized conditions described in subsection 8.2. In Figure 10, the absolute error is
reflects the model error that the Gaussian beam does not satisfy the idealized conditions described in subsection 8.2. In Figure 10, the absolute error is![]() , In data generation, we used
, In data generation, we used![]() . If we used a different value for
. If we used a different value for![]() , it would not change the absolute error
, it would not change the absolute error![]() .
.
3) The prediction is invariant with respect to a scaling of![]() . Suppose the true value of
. Suppose the true value of ![]() is not measurable. Instead, a quantity proportional to
is not measurable. Instead, a quantity proportional to ![]() with a fixed but unknown multiplier is measured. Let
with a fixed but unknown multiplier is measured. Let ![]() be the measured quantity where
be the measured quantity where ![]() is an unknown coefficient. For example, while it may be difficult to measure the power density deposited on the skin (
is an unknown coefficient. For example, while it may be difficult to measure the power density deposited on the skin (![]() ), the power emitted at the antenna (Q) is proportional to
), the power emitted at the antenna (Q) is proportional to ![]() and is measured in experiments. The 3 data points with Q as the independent variable are at
and is measured in experiments. The 3 data points with Q as the independent variable are at ![]() and
and ![]() where
where![]() . Here
. Here ![]() is measured/specified but both
is measured/specified but both ![]() and
and ![]() are unknown. Let
are unknown. Let ![]() be the solution of Equation (44) with Q as the independent variable. We have
be the solution of Equation (44) with Q as the independent variable. We have
![]()
The predicted observed reflex time as a function of Q satisfies
![]()
Therefore, for the purpose of determining![]() , we only need to measure
, we only need to measure![]() . There is no need to measure
. There is no need to measure ![]() or find the value of multiplier
or find the value of multiplier![]() .
.
It is worthwhile to point out that all of the properties above are attributed to the formulation form of (44). They are independent of the data on which algorithm (44) is applied. In particular, they are not affected by the true model governing the data generation in simulations or in experiments. Property 3 above is very powerful in applications. To estimate the time delay![]() , it is sufficient to measure i) the power emitted at the antenna (Q) and ii) the corresponding observed reflex time (
, it is sufficient to measure i) the power emitted at the antenna (Q) and ii) the corresponding observed reflex time (![]() ). Both of these are readily measurable. In algorithm (44), using the measurable quantity Q as the independent variable instead of
). Both of these are readily measurable. In algorithm (44), using the measurable quantity Q as the independent variable instead of ![]() does not introduce any additional error in estimating the time delay
does not introduce any additional error in estimating the time delay![]() . Formulation (44) is truly invariant with respect to scaling.
. Formulation (44) is truly invariant with respect to scaling.
8.4. Energy Consumption vs. Applied Power
Let ![]() be the power absorbed in the skin (energy absorbed per time) and
be the power absorbed in the skin (energy absorbed per time) and ![]() be the power emitted at the antenna of radiators. At a fixed beam radius w and at a fixed distance d between the antenna and the test subject,
be the power emitted at the antenna of radiators. At a fixed beam radius w and at a fixed distance d between the antenna and the test subject, ![]() is proportional to
is proportional to![]() , which in turn is proportional to
, which in turn is proportional to![]() , the power density absorbed in the skin at the beam center.
, the power density absorbed in the skin at the beam center.
![]()
![]()
The proportionality constant ![]() is independent of
is independent of![]() .
.
Let ![]() be the total energy emitted at the antenna by the time of withdrawal reflex
be the total energy emitted at the antenna by the time of withdrawal reflex![]() . Energy
. Energy ![]() is proportional to
is proportional to ![]()
![]()
We treat ![]() as the energy consumption and study it as a function of applied power density
as the energy consumption and study it as a function of applied power density![]() . Since the proportionality constant
. Since the proportionality constant ![]() is independent of
is independent of![]() , we use
, we use ![]() as a measure of energy consumption. Figure 11 plots
as a measure of energy consumption. Figure 11 plots ![]() vs
vs ![]() for a Gaussian beam. In Figure 11, the energy consumption varies with the applied power density and it attains a minimum at a moderate value of
for a Gaussian beam. In Figure 11, the energy consumption varies with the applied power density and it attains a minimum at a moderate value of![]() .
.
In case B, we showed analytically (in subsection 7.4) that the energy consumption attains a minimum at an intermediate range of applied power density. The minimum energy consumption is attributed to the two opposite effects of heat conduction on temperature increase, respectively over short time and over long time. In case B, with a given beam spot area, withdrawal reflex occurs when the temperature at a fixed depth reaches the nociceptor activation temperature. Mathematically, we derived (in subsection 7.3) that at a fixed depth, over short time the net heat gain via conduction is positive. When the applied power is large, the reflex occurs in short time. Over that short time, the heat conduction augments the temperature increase of electromagnetic heating, speeds up the process of reaching the activation temperature, and reduces the energy consumption. In the regime of large applied power, increasing the applied power further makes the reflex time very short and leaves very little time for the conduction to take its effect in reducing the energy consumption. As a result, in the regime of large
![]()
Figure 11. Energy consumption by the reflex time![]() .
.
applied power, the energy consumption increases with the applied power. At a given depth, the positive net heat gain via conduction depends on the heat in-flow from upstream. At the skin surface, however, there is no heat in-flow. As time goes on, the effect of insulated boundary propagates in the depth direction in the form of attenuating the heat flow. Mathematically, at a fixed depth, eventually the net heat gain via conduction turns negative and the magnitude of net heat loss grows with time. When the applied power is small, it takes long time to induce the reflex. Over that long time, the heat conduction yields net heat loss, diminishes the temperature increase of electromagnetic heating, slows down the process of reaching the activation temperature, and drives up the energy consumption. In the regime of small applied power, reducing the applied power will give the conduction more time to take its effect in neutralizing the electromagnetic heating, and increase the energy consumption. Consequently, In the regime of small applied power, the energy consumption increases when the applied power is lowered. The transition between these two regimes produces a minimum for the energy consumption. Although the behaviors of these two regimes were derived for the idealized case B, in the case of a Gaussian beam, we observe the same behaviors in Figure 11: in the regime of small ![]() when
when ![]() increases, energy consumption is reduced; in the regime of large
increases, energy consumption is reduced; in the regime of large![]() , energy consumption increases with
, energy consumption increases with![]() ; the transition between these two trends produce a minimum energy consumption in the middle. Figure 11 indicates that the two opposite effects of heat conduction on temperature increase, respectively over short time and over long time, are present in all situations even when the idealized conditions are not met.
; the transition between these two trends produce a minimum energy consumption in the middle. Figure 11 indicates that the two opposite effects of heat conduction on temperature increase, respectively over short time and over long time, are present in all situations even when the idealized conditions are not met.
Figure 11 describes the energy consumption in the situation where the power is turned off exactly at the predicted internal initiation of withdrawal reflex (before the actual occurrence of observed reflex). Given that the predicted ![]() is not exact, to ensure that the applied beam induce the withdrawal reflex, it is prudent to keep the power on for a short time beyond
is not exact, to ensure that the applied beam induce the withdrawal reflex, it is prudent to keep the power on for a short time beyond![]() . In real operations, adding a short time serves as a cushion for accommodating the uncertainty in estimating
. In real operations, adding a short time serves as a cushion for accommodating the uncertainty in estimating![]() . The uncertainty is in the form of an absolute error in the estimated
. The uncertainty is in the form of an absolute error in the estimated![]() , which leads to an absolute error in the estimated true reflex time
, which leads to an absolute error in the estimated true reflex time![]() . We study the energy consumption until (
. We study the energy consumption until (![]() + cushion time), as a function of applied power density. Figure 12 plots
+ cushion time), as a function of applied power density. Figure 12 plots ![]() vs
vs![]() . With a fixed short time 0.05 added to
. With a fixed short time 0.05 added to![]() , the energy consumption has a more pronounced minimum, which also occurs at a more moderate range of applied power.
, the energy consumption has a more pronounced minimum, which also occurs at a more moderate range of applied power.
8.5. Determining ![]() from Test Data
from Test Data
In subsection 7.6, we discussed selecting test conditions for producing distinct constraint functions on ![]() in the idealized case B. We found that a combination of large beam spot area
in the idealized case B. We found that a combination of large beam spot area ![]() and moderate applied power density
and moderate applied power density ![]() yields a flat
yields a flat ![]() vs
vs ![]() while a combination of moderate
while a combination of moderate ![]() and
and
large ![]() gives a slant
gives a slant ![]() vs
vs![]() . In this subsection, we test this strategy in the case of a Gaussian beam.
. In this subsection, we test this strategy in the case of a Gaussian beam.
We use the temperature distribution given in (61). To mimic the situation of real applications, we work with![]() , the physical temperature in physical coordinates. In simulations of this subsection, we use
, the physical temperature in physical coordinates. In simulations of this subsection, we use
![]()
Here, for clarity, we reserve ![]() as the notation for the true value of
as the notation for the true value of ![]() and use the general notation
and use the general notation ![]() to represent the variables in constraint functions. We run simulations using the parameters listed above with various combinations of
to represent the variables in constraint functions. We run simulations using the parameters listed above with various combinations of ![]() to generate simulated data sets. Each data set consists of the reflex time
to generate simulated data sets. Each data set consists of the reflex time ![]() and the temperature distribution
and the temperature distribution ![]() for a particular test condition
for a particular test condition![]() . For each data set, we apply formulation (5) described in section 4 to construct a constraint function on
. For each data set, we apply formulation (5) described in section 4 to construct a constraint function on![]() . Formulation (5) is based solely on the data of spatial temperature profile at reflex
. Formulation (5) is based solely on the data of spatial temperature profile at reflex![]() . It does not require any input parameter. Figure 13 displays constraint functions for 3 combinations of
. It does not require any input parameter. Figure 13 displays constraint functions for 3 combinations of![]() . It demonstrates the same behaviors as we observed in case B: increasing the beam radius w makes the constraint curve
. It demonstrates the same behaviors as we observed in case B: increasing the beam radius w makes the constraint curve ![]() vs
vs ![]() flat while decreasing w makes the curve slate. The intersection of distinct constraint curves gives us the true value
flat while decreasing w makes the curve slate. The intersection of distinct constraint curves gives us the true value![]() .
.
9. Concluding Remarks
We studied theoretically the occurrence of heat-induced withdrawal reflex caused by exposure to an electromagnetic beam. We investigated several aspects of the problem, including i) non-dimensionalization to pinpoint the effects of parameters; ii) normalization of the non-dimensional temperature into a parameter-free function; iii) forward prediction of system behaviors given model
![]()
Figure 13. Constraint functions constructed from simulated data for a Gaussian beam. Three distinct constraint curves are shown, corresponding to three test conditions.
Parameters; iv) asymptotic behaviors in certain regimes of parameters; and v) backward inference of model parameters based on measured data.
First, we reviewed the model components used in ADT CHEETEH-E [17], and we synthesized them to distill a concise dose-response model for predicting the occurrence of withdrawal reflex based on the given spatial temperature profile. In the dose-response relation, the dose quantity is defined as the volume of the activated region of heat-sensitive nociceptors. Under the assumption that the nociceptor density is uniform in the skin, the activated volume is proportional to the total number of nociceptors activated, and thus, increases monotonically with the perceived pain level, which controls the occurrence of withdrawal reflex. In a deterministic setting, withdrawal reflex occurs precisely when the activated volume reaches a critical threshold. The resulting dose-response relation described in (4) is specified by two parameters: the nociceptor activation temperature ![]() and the critical threshold
and the critical threshold ![]() on the activated volume for withdrawal reflex.
on the activated volume for withdrawal reflex.
The concise model has the advantage that the two parameters can be determined from test data in the situation where the reflex time and the spatial temperature profile at reflex are measurable. Parameters ![]() and
and ![]() are constrained by function (5), which is constructed solely from the measured temperature profile at reflex. The inference method based on (5) is parameter-free, requiring no input parameter. The data set measured at each test condition provides only one constraint on
are constrained by function (5), which is constructed solely from the measured temperature profile at reflex. The inference method based on (5) is parameter-free, requiring no input parameter. The data set measured at each test condition provides only one constraint on![]() . To determine the two unknown parameters, several tests at various conditions are needed to produce distinct constraint functions. The intersection of distinct constraint curves yields the true value
. To determine the two unknown parameters, several tests at various conditions are needed to produce distinct constraint functions. The intersection of distinct constraint curves yields the true value![]() .
.
The dose-response relation predicts the occurrence of withdrawal reflex from the given spatial temperature profile. We connected it with a time evolution model for the temperature increase of electromagnetic heating. The result is a composite model that takes as input the test condition described by two tunable quantities: the beam spot area and the applied power density. Other quantities, such as the initial temperature, the characteristic depth of the electromagnetic wave penetrating into the skin and the nociceptor activation temperature, are viewed as parameters. In the composite model, the time evolution model produces the temperature distribution from the test condition, and then the dose-response relation uses the temperature distribution to determine the time of withdrawal reflex. We solved the composite model analytically in two idealized cases, first in the case of no heat conduction and uniform electromagnetic heating over beam cross-section (case A).
To examine the validity of the no-conduction assumption, we investigated the effect of heat conduction on temperature distribution. In the case of uniform electromagnetic heating over beam cross-section with heat conduction in the depth direction (case B), we carried out non-dimensionalization to facilitate the exact solution and to pinpoint the effects of model parameters. We solved the non-dimensional system analytically to obtain the exact solution given in (22). As a function of non-dimensional time and depth, the non-dimensional temperature is the product of the non-dimensional power density and a parameter-free function, which is called the normalized temperature. The normalized temperature has no dependence on the power density or any other parameters. The effects of physical parameters are contained in the non-dimensional variables and quantities. Scaling temperature distribution into a parameter-free function significantly simplifies the structure of exact solution and reveals its dependence on parameters. We compared the normalized temperatures in the presence and in the absence of heat conduction. We found that the no-conduction approximation is valid only in the region away from the skin surface and only over a short time. Both conditions need to be satisfied in order to make the effect of heat conduction negligible. This result indicates that the no-conduction approximation is not an adequate tool for analyzing the temperature evolution near the skin surface.
Using the exact solution obtained in case B (the case with heat conduction), we studied theoretical behaviors of the system. Below are the findings.
· As the beam spot area A increases, the reflex time decreases rapidly to a positive value above zero. The convergence is described by 1/A2 in (34).
· We define the true reflex time as the moment when the number of activated nociceptors is sufficiently large to produce a perceived pain level exceeding the tolerance and thus to initiate the withdrawal reflex. The observed reflex time is when the reflex response (i.e., the subject moving out of the beam) actually takes place. There is a latency (time delay) between the observed reflex time and the true reflex time. We assume that the latency is intrinsic to the subject being tested and is independent of the applied power density. We derived algorithm (44) for inferring the time delay from measured values of observed reflex times at a sequence of applied power density values. Once the time delay is obtained, the true reflex time is calculated from the observed reflex time.
· The true reflex time decreases when the applied power density is increased. To examine the behaviors respectively at large and at small applied power density, we carried out asymptotic expansions of the normalized temperature respectively for small and large time. From the expansions of the normalized temperature, we derived asymptotic approximations of the reflex time, respectively, for large applied power density given in (51) and for small power density given in (52). At a fixed beam spot area, the product of beam power density and reflex time is proportional to the energy consumed for inducing withdrawal reflex. The asymptotic analysis indicates that when we increase the power density gradually in the small regime, initially the energy consumption decreases and then it attains a minimum; eventually in the large regime, further increase of power density leads to an increase in energy consumption. The two sides of the energy consumption curve surrounding the minimum correspond to the two opposite effects of heat conduction, respectively over short time and over long time. At a fixed depth, over short time, heat conduction augments the temperature increase of electromagnetic heating. It leads to a temperature growth faster than the no-conduction solution and reduces the energy consumption by shortening the reflex time. In contrast, over long time, heat conduction diminishes the temperature increase of electromagnetic heating. It results in a much slower temperature growth than the no-conduction solution and drives up the energy consumption needed for inducing withdrawal reflex.
· We examined the spatial temperature profile at reflex and how it varies with the applied power density. We found that at a fixed depth, for large power density, the temperature at reflex converges to the no-conduction solution. This result indicates that it is appropriate to neglect the effect of heat conduction only when the location is away from the skin surface and when the (non-dimensional) power density is large.
· In the situation where the spatial temperature profile at reflex is measured in tests, we studied the methodology for determining ![]() from test data.
from test data. ![]() is constrained by Equation (5), which is parameter-free and is constructed based solely on the measured spatial temperature profile. The intersection of two or more distinct constraint curves, calculated from test data at various test conditions, determines the true value
is constrained by Equation (5), which is parameter-free and is constructed based solely on the measured spatial temperature profile. The intersection of two or more distinct constraint curves, calculated from test data at various test conditions, determines the true value![]() . We explored how to select test conditions to produce significantly distinct constraints on
. We explored how to select test conditions to produce significantly distinct constraints on![]() . We found that the steepness of
. We found that the steepness of ![]() is negatively associated with the beam spot area. For the purpose of estimating
is negatively associated with the beam spot area. For the purpose of estimating![]() , we need to carry out tests with moderate beam spot area and with large beam spot area. This is to ensure that the constraint curves constructed from test data are substantially distinct and have a well-defined intersection.
, we need to carry out tests with moderate beam spot area and with large beam spot area. This is to ensure that the constraint curves constructed from test data are substantially distinct and have a well-defined intersection.
We conducted a case study of a Gaussian beam with finite beam radius and with heat conduction in the depth direction. Since it has no closed-form solution, the case study was carried out using numerical simulations. The goal was to test the theoretical results predicted for the idealized case of uniform temperature over beam cross-section (case B). We first examined the performance of algorithm (44) for determining the unknown latency from measured values of observed reflex times at a sequence of applied power density values. Algorithm (44) was derived under the assumptions of case B and in the limit of beam spot area approaching infinity. (44) calculates the time delay solely from 3 data points of ![]() where
where ![]() is the applied power density and
is the applied power density and ![]() is the corresponding observed reflex time. Algorithm (44) does not require any input parameter. Operationally, it is universally applicable in all situations where the observed reflex time is measured. We applied it to the case of a Gaussian beam with a finite beam radius. In Figure 10, the estimated time delay is very close to the true value, suggesting the wide applicability of algorithm (44) beyond the idealized case B.
is the corresponding observed reflex time. Algorithm (44) does not require any input parameter. Operationally, it is universally applicable in all situations where the observed reflex time is measured. We applied it to the case of a Gaussian beam with a finite beam radius. In Figure 10, the estimated time delay is very close to the true value, suggesting the wide applicability of algorithm (44) beyond the idealized case B.
In addition to its high accuracy, formulation (44) has an important scaling property: the prediction by (44) is invariant with respect to a scaling in the independent variable![]() . At a fixed beam radius and fixed distance from the test subject, the power emitted at the antenna is proportional to the beam center power density. The scaling property allows us to use the power emitted at the antenna as the independent variable in (44). The calculation of
. At a fixed beam radius and fixed distance from the test subject, the power emitted at the antenna is proportional to the beam center power density. The scaling property allows us to use the power emitted at the antenna as the independent variable in (44). The calculation of ![]() in (44) is independent of the proportionality constant in scaling. The time delay calculated this way will be the same as if we use the beam center power density as the independent variable in (44). This scaling property is especially useful when it is impractical to measure the beam center power density deposited on the skin.
in (44) is independent of the proportionality constant in scaling. The time delay calculated this way will be the same as if we use the beam center power density as the independent variable in (44). This scaling property is especially useful when it is impractical to measure the beam center power density deposited on the skin.
In the case of a Gaussian beam, we examined numerically the energy consumption for inducing withdrawal reflex as a function of applied power density. We first considered the situation where the power is turned off at the true reflex time when the activated volume reaches the threshold to start the internal initiation of withdrawal reflex. The observed reflex action (the subject moving out of beam) occurs with time delay ![]() after the internal initiation. We observed that a minimum energy consumption is attained at a moderately large beam center power density, similar to what we theoretically predicted in the idealized case B. This observation suggests that the existence of minimum energy consumption may be a general phenomenon in all situations. In the situation where we keep the power on for a short period beyond the true reflex time, the energy consumption has a more pronounced minimum, which is attained at a more moderate value of the applied power density.
after the internal initiation. We observed that a minimum energy consumption is attained at a moderately large beam center power density, similar to what we theoretically predicted in the idealized case B. This observation suggests that the existence of minimum energy consumption may be a general phenomenon in all situations. In the situation where we keep the power on for a short period beyond the true reflex time, the energy consumption has a more pronounced minimum, which is attained at a more moderate value of the applied power density.
In the case of a Gaussian beam, we tested the strategy of selecting test conditions for determining parameters ![]() and
and![]() . Again, the theoretical behavior of constraint function
. Again, the theoretical behavior of constraint function![]() , established in the idealized case B, remains qualitatively true for a Gaussian beam: the slope of constraint function
, established in the idealized case B, remains qualitatively true for a Gaussian beam: the slope of constraint function ![]() decreases when the beam size is increased. To obtain substantially distinct constraint curves for
decreases when the beam size is increased. To obtain substantially distinct constraint curves for![]() , we need to carry out tests with a moderate beam radius and with a large beam radius.
, we need to carry out tests with a moderate beam radius and with a large beam radius.
In summary, in a deterministic setting, we studied mathematically the system from the electromagnetic power deposited on the subject’s skin to the subject’s behavioral response. Our theoretical findings provide insight into how the system behaves in various regimes of model parameters and how the system behavior varies in response to changes in parameters. Furthermore, through theoretical formulation and analysis in idealized cases, we established a mathematical framework for designing tunable parameters in tests to fully sample the effects of hidden parameters in test data. Properly sampling the effects of model parameters in test data is a vital step toward reliably determining the values of these parameters.
Acknowledgements and Disclaimer
The authors thank Dr. John Biddle and Dr. Stacy Teng of the Institute for Defense Analyses for introducing the ADT CHEETEH-E model and for many helpful discussions. The authors acknowledge the Joint Non-Lethal Weapons Directorate of U.S. Department of Defense and the Naval Postgraduate School for supporting this work. The views expressed in this document are those of the authors and do not reflect the official policy or position of the Department of Defense or the U.S. Government.
Appendix A: Exact Solution of Case A
In case A defined in (9), the temperature distribution ![]() is governed by
is governed by
![]()
Integrating with respect to t yields the temperature distribution
![]() (65)
(65)
Since case A is a special situation of case U, the reflex time ![]() is governed by Equation (8). With the expression of
is governed by Equation (8). With the expression of ![]() given in (65), equation for
given in (65), equation for ![]() becomes
becomes
![]()
Solving for![]() , we obtain
, we obtain
![]() (2)
(2)
Appendix B: Analytic Expression of Function ![]()
Recall that ![]() is defined as the solution of
is defined as the solution of
![]()
To solve for![]() , we first convert the initial boundary value problem to an initial value problem by extending the initial condition for
, we first convert the initial boundary value problem to an initial value problem by extending the initial condition for ![]() to an even function of y.
to an even function of y.
![]()
Using the fundamental solution of the heat equation, we write ![]() as
as
![]()
Completing the square in the exponent of term![]() , we get
, we get
![]()
Similarly, we can derive
![]()
Substituting ![]() and
and ![]() into the expression of
into the expression of![]() , we arrive at
, we arrive at
![]() (67)
(67)
Appendix C: Asymptotics of Functions![]() ,
, ![]() and
and ![]()
Recall that function ![]() is defined in (42) in terms of
is defined in (42) in terms of![]() . Function
. Function ![]() is
is
![]()
We carry out analysis in steps below to derive the asymptotics of![]() .
.
Step 1: We first show that ![]() is well defined. We show that for
is well defined. We show that for ![]() , function
, function ![]() increases with t, and its range is
increases with t, and its range is![]() .
.
Noticing that ![]() and
and![]() . To prove that the range of
. To prove that the range of ![]() is
is![]() , we derive the asymptotic of
, we derive the asymptotic of ![]() for large t. We write
for large t. We write ![]() as
as
![]()
where ![]() is the scaled complementary error function and has the expansion
is the scaled complementary error function and has the expansion
![]() (68)
(68)
Using (68), we write out the expansion of ![]() for large t
for large t
![]() (69)
(69)
As t goes to infinity, ![]() increases unbounded. Thus, the range of
increases unbounded. Thus, the range of ![]() is
is![]() .
.
Step 2: Using the results of ![]() obtained in Step 1, we see that
obtained in Step 1, we see that ![]() is well defined for
is well defined for![]() . In this step, we derive the expansion of
. In this step, we derive the expansion of ![]() for large u.
for large u.
We notice that u as a function of ![]() has the expansion given in (69).
has the expansion given in (69).
![]()
Based on this, we write out an iterative formula for expanding ![]()
![]()
Starting the iteration with![]() , we calculate
, we calculate![]() ,
, ![]() and
and
![]()
Squaring both sides, we obtain the expansion of ![]() as a function of u.
as a function of u.
![]() (70)
(70)
Step 3: In this step, we expand ![]() for large u. Using (6), we write
for large u. Using (6), we write
![]()
![]() (71)
(71)
Step 4: In this step, we expand ![]() for small u. We start with the expansion of
for small u. We start with the expansion of ![]()
![]() (72)
(72)
Based on this, we write out an iterative formula for expanding ![]()
![]()
Starting the iteration with![]() , we calculate
, we calculate![]() ,
, ![]() , and
, and
![]()
Thus, near ![]() function
function ![]() has the expansion
has the expansion
![]() (73)
(73)
Step 5: In this step, we expand ![]() for small u. Using (73), we write
for small u. Using (73), we write
![]()
![]() (74)
(74)
Appendix D: Calculation of ![]() in Expansion (47)
in Expansion (47)
The expansion of ![]() for large t is given in (47) with
for large t is given in (47) with ![]() undetermined. Recall that
undetermined. Recall that ![]() is governed by Equation (20). To derive
is governed by Equation (20). To derive![]() , we substituting expansion (47) into (20). The balance of leading terms gives us
, we substituting expansion (47) into (20). The balance of leading terms gives us ![]() , which leads to
, which leads to
![]()
The insulated boundary condition ![]() yields
yields![]() . To determine
. To determine![]() , we compare the expansion of
, we compare the expansion of ![]() for large t given in (69) with expansion (47) at
for large t given in (69) with expansion (47) at![]() . We obtain
. We obtain![]() . Thus,
. Thus, ![]() in expansion (47) has the expression
in expansion (47) has the expression
![]() .
.