Developed Numerical Simulation of Falling and Moving Objects in Viscous Fluids under the Action of a Reynolds Lubrication Theory and Low Reynolds Numbers ()
1. Introduction
In many areas of science and engineering, the flow of viscous fluids at low Reynolds number plays an important role, especially in applied areas of lubrication theory and micro-organism locomotion. This work focuses on the simulation of very slow motion of solid bodies in viscous fluids, inspired by applications in micro-fluidics and bio-mechanics. Viscous flow past in a sphere and in a circular cylinder at very low Reynolds number was first analyzed by Stokes [1].
At low Reynolds number, the inertia of the surrounding fluid becomes unimportant in comparison with viscous forces and thus is generally neglected. Thus the flow is dominated by the viscous forces and the problem is termed as the Stokes-flow problem. It is usually difficult to formulate the exact or approximate solutions for the sphere, ellipsoids and long cylinder body shapes [2]. To solve the Stokes flow problem approximately, two analytical methods are very well known. One is the boundary-value method and the other is the singularity method. The most important special case is that of the exact solution to Stokes’ flow problem using the motion of an ellipsoid derived by [3] [4] [5]. Their solution is based on the boundary value problem.
The axi-symmetric slender-body theory is using singularity method at low Reynolds number flow, which has been studied by [2] [6] - [14] and others. More complete formulations of the asymptotic motion of slender axi-symmetric rigid bodies have been done by Geer [15], Keller and Rubinow [16] and non-axially symmetric straight bodies also have been studied by Batchelor [11]. Recently, in the limit of zero Reynolds number, the slender-body theory has been studied by Butler and Shaqfeh [17], Tornberg and Gustavsson [18]. Butler and Shaqfeh [17] have delivered far-field and short-range interaction between particles. For slender bodies of non-spherical shapes at short ranges [17] have used the lubrication theory while for simulation algorithms they have used slender-body theory to model linear and angular velocity and force distribution along the centerline of each thin objects, they have used periodic boundary conditions for non-spherical body shape. The paper by Geer [15] has the treatment of circular cross-section of axi-symmetric rigid body shape and Batchelor [11] has demonstrated the case of non-circular cross-section of non-axial symmetric straight body.
The developed numerical simulation focused on the flow of a viscous fluid at low velocities around a slender body. Considering two different model settings: vertical and spherical shape cylindrical models have been used and theoretical calculation has carried out by Reynolds Lubrication Theory. For the simulation of vertical cylindrical and spherical models, the fluid tank is assumed to be non axi-symmetric, and calculation has been carried out for both models. For the simulation algorithms, polar coordinate system based on lubrication theory is imposed. This is utilized for all short-range calculations including calculation of force and velocity distributions. The results from the numerical simulation (COMSOL) are compared to the analytical approximation (Matlab), and the numerical solutions for vertical and spherical models are very close to the analytical approximation solutions.
In addition, for most macroscopic fluid dynamics processes, inertia forces dominate, and the propulsion systems of swimmers and manmade crafts exploit the lift forces created by the re-direction of the flow by moving surfaces. Slow swimming in very viscous fluids is a very different proposition [19] explains how. Hancock [6] first considered the usage of “Resistive Theory” in the theoretical development of flagella motion. Johnson and Brokaw [20] surmised that the flagellum would be able to swim provided the average force exerted by the flagella on the fluids is non-zero. Jeffery [5] has been first introduced ellipsoid shape of particle and has given formula for the increase of viscosity.
In addition, the particular aim of the study here is to perform numerical simulations of motion of development microscopic organ in viscous fluids with reference to the stationary boundary wall. For a solitary particle in motion in a viscous fluid, firstly the forces between the boundary walls and the moving body are considered. The worm like 2D body swims past a travelling wave such that its motion is constrained along the centerline of its body. COMSOL3.5a and Matlab software with predefined models for Navier-Stokes and Stokes flow are employed to solve the problem numerically. A moving coordinate system has been used to describe the ellipsoidal particle swimming in the viscous fluid. The resulting force and torque are calculating along with linear and angular velocity of the ellipsoidal body. This is calculated on the basis that net force and torque on the object are zero. The result shows the force and torque that is exerted on the swimming object by the viscous fluid and swimming object is moving slowly in one position to another through small amplitude and wavelengths.
2. Methodology and Methods
2.1. Physical Description
Conceptual Models for Simulation of Falling and Moving Objects in a Viscous Fluid
The cylindrical and spherical cases are designed to simulate the motion of very thin objects under gravity in a fluid. The collective motion of many of such objects is studied in Linström and Uesaka [21], Tornberg and Gustavsson [18]. How such a thin object is related when it approaches the bottom is important, and it is found that the retarding force is the pressure field resulting form squeezing out the liquid between the thin object and the plane bottom [18]. As illustrated by the analysis and calculations here, the thin object, however, does not sense the bottom until the distance is on the order of the fiber diameter, a length scale which is uncomfortable for the simulations. The vertical cylinder and the spherical model have a line of symmetry to the vertical. One can visualize the vertical cylinder and the sphere falling along their lines of vertical symmetry when introduced into a tank containing viscous fluid. The coordinate directions of interest in vertical cylinder and spherical cases are the radial direction r and the direction of the vertical axis z. The governing equation for these models as stated earlier is the Stokes flow equation (Figure 1(a) and Figure 1(b)).
The fluid velocity u matches the movement of the body surface, and, in response, the fluid exerts a force f on the surface. The computational domain is bounded by a wall, which is assumed to be stationary. In order to obtain smooth and exact solutions, we introduce slight compressibility. This change gives a unique pressure even in the absence of pressure boundary conditions. Since the flow is bounded by (slip or no-slip) walls, one has to ensure that the velocity specified on the body surface is nearly compatible with incompressible flow i.e., the body volume must be held constant. Continuing from here, we compute the velocity and pressure. Then we observe the forces in the models when they have reached near the bottom wall of the tank.
In second experiment Figure 1(c), consider two-dimensional ellipsoid body that is swimming or moving in a viscous incompressible fluid at low Reynolds number. The locomotion of microscopic organisms [22] [23] [24] is an example of swimming at low Reynolds number. The motion of particles in Stokes flows is important in many biological systems. Blood platelets are spheroidal or ellipsoidal and bacteria swim with the aid of flagella or cilia [25].
Swimming at the small scales relevant to cell swimming that tens of micro-meters and below when it’s submerged in a viscous fluid [26]. It is possible for small objects to move when fluid is viscous or at low Reynolds number [27]. If the solid object motion is symmetric in time, then it is called as periodic motion [28].
![]()
Figure 1. Falling objects and body moving at small Re number in a bounded domain. (a) Vertical cylinder in tank; (b) Sphere in tank; (c) Moving Object.
In situations like this, the reciprocal theorem becomes applicable [29]. Single degree of freedom movement is known to be reciprocal motion [19]. If an object is capable of reciprocal motion then it has one degree of freedom configuration. This implies that time is not of significance and that there is no difference between fast and slow movements. The application of periodic boundary conditions results in periodic motion. Consider an object which has been introduced to a tank which is filled with viscous fluid. In the fluid dynamic equations, if the body moves at some average velocity then the average force must be zero [25] [16] [30]. That means calculation of force and torque on the object by the surrounding fluid in terms of the specified object motion. The unknown linear and angular velocity are determined by the condition that the net force and torque on the organism are zero [31].
2.2. Governing Equations
2.2.1. Low Reynolds Number Flow
Low Reynolds number viscous flow past a sphere and a circular cylinder has been analysed by [1] [27] etc. Low Reynolds number flow is characterised by low velocities and dominant viscosity effects. The case where the solution is stable and linear under low Reynolds number flow is governed by the so-called slow flow equations or the Stokes equations. The Stokes equation is a special case of the Navier Stokes equations. At low Reynolds numbers, inertial forces are negligible viscous forces tend to dominate. This is almost the case of zero Reynolds number [32]. The reduction of Navier Stokes equations to Stokes equations brings in time independence and there is really no difference between slow and quick swimming as demonstrated by [33]. It might also be noted that Stokes flow is also called the reciprocal theorem [26]. The governing equations of Stokes flow are Partial Differential Equations (PDE’s) of the elliptic type.
When we apply the velocity boundary condition on the surface of an ellipsoidal, spherical or any other experimental body, the body being in a viscous fluid tends to slow down. This is due to the effect of viscous forces, which impair the motion of the body. The system behavior is strongly viscous, and the so-called creeping motion or Stoke Equations [34] govern their behavior.
2.2.2. Derivation of Stokes Equation
The Navier-Stokes equations describe flow in viscous fluids with momentum balances for each component of the momentum vector in all spatial dimensions. The study focus on the boundary movement and swimming at low Reynolds number flow that is either very viscous, very slow, or very small. Low Reynolds number flow for water is about 10 to 4 m2⁄s. Flows with small Re are also called creeping flows or Stokes slow and appear on small scales in porous media, in micro-fluidic devices, and flows with small bodies such as bacteria, amoeba, and innate particles such as blood corpuscles, droplets, bubbles, and mineral grains. However, the inertial forces are negligible also in very large-scale geological movements such as glacier flow and tectonic plate movement. Important thing is that the low Reynolds number flow plays an important role in the study or lubrication theory, moving micro-organism and many area of biophysical and geophysical interest [27].
The Stokes Flow equations for creeping flow are obtained as the
limit of the Navier-Stokes equations for momentum balance augmented by the mass balance law [19], and the fluid flow has made slightly compressible,
, where
. The slightly compressible Stokes equation can be written as,
(1)
The Stokes Equation (1) with boundary conditions of specified body surface velocities. This is a linear system of PDE, and it follows that the velocity field and hence the forces exerted by the fluid on a moving body are linear and the body surface velocities are proportional to
.
2.2.3. Reynolds Lubrication Theory (RLT)
For the analysis of the thin layer fluid flow between cylindrical and spherical object and bottom wall of the tank, the Reynolds Lubrication theory is used which is generally called the Lubrication theory. It is a most important approximation of Stokes equation whenever one of the dimensions of the system is small compared to the others [35] [36].
A body with the surface
is considered close to a solid plane at
. One can regard the gap as “thin” provided that “h” is small, and the pressure z-gradient can be neglected as well as the momentum transport terms,
Integration across the layer of the mass balance results in the Reynolds lubrication equation,
(2)
If the body is rigid and moving in the z-direction, we have
.
1) For Vertical Cylindrical Model (RLT)
For the vertical cylinder, we have axial symmetric axis,
(3)
2) For Spherical Model (RLT)
For the sphere there is axi-symmetry, so with r the radial polar coordinate,
(4)
2.2.4. Body Movement
A long body performs a wiggling motion, a sinusoidal lateral (η) displacement of every point on its surface, as traveling waves,
(5)
This motion, combined with translation and rotation of the local coordinate system, keeps body volume constant, but the body perimeter is not constant. The dimension of the object chosen in this simulation is 0.002 m and the shape of the moving object is elliptical. The wiggling amplitude
is small, on the order of the worm thickness, and the worm length is a few wavelength
. In Figure 2, a snapshot of an elliptical striped worm about two wavelengths long is shown.
The angular frequency is immaterial in the sense that the wiggle motion is periodic in time and the body has moved a certain distance per period. Consider the calculation of the swimming velocities of the model object. This model is designed by small amplitude to deform the surface of the swimmer. Small amplitude body motion is periodic motion.
For deformation or swimming of the object, we have chosen non-reversible flow. This means flow is going forward and backward but moving object has no way to go back to the original position. When we have chosen the moving boundary condition, allow re-meshing and use time dependent solver then we see the mesh deform and the object move. This means that the fluid particle is swimming periodically on average.
When we differentiate Equation (5) with respect to t then we get the velocity in the moving frame
(6)
For the forward swimming motion, we calculate the force and torque that is exerted on the object by the domain fluid and also calculate the unknown linear and angular velocity of the swimmer object whose net force and torque on the object are zero.
The transformation from local coordinates to the global coordinates (see Figure 2) is
(7)
![]()
Figure 2. Elliptrical striped worm of two wavelengths long.
where,
.
Then, on the boundary of the wiggling swimmer (see Figure 2),
(8)
where,
must be computed from global coordinates
,
(9)
These are the velocities of a point on the swimmer surface, used as boundary condition for the Stokes equation. From that solution, the forces f on the surface S are calculated, and the net forces and moment on the body,
(10)
The sum of internal forces of all bodies are zero, the balance of linear and angular momentum for the deforming body take the form,
If the body were rigid, these equations would determine the motion of its centre of gravity and the angle θ of rotation, the three 2D rigid-body degrees of freedom. For the deforming body there is in general no such convenient reduction.
However, in the limit of small inertial forces, the acceleration terms vanish and we are left with
(11)
consistent with the neglecting of inertial forces as expressed by the Stokes flow model. For numerical reasons, we have implemented the singular perturbation model of (11)
(12)
where “m” and “J” are “small”. Since inertia forces are neglected in the momentum balance for the fluid, this is an inconsistent approximation.
However, it shows that if the system is stable, i.e. that the forces tend to act against the velocities, then there should be a well-defined limit as “m” and “J” vanish and it should be the solution of the differential-algebraic system, Equation (12). The numerical implementation uses the Ordinary Differential Equations (ODE) system with small “m” and “J”.
The ODE is used for differential algebraic equations or to add degrees of freedom to a PDE (Partial Differential Equations) using the introduced states. First time derivative represents velocity and second time derivative represents force and moment in ODE setting. In ODE system, there is no need to find consistent initial values for
,
and W. “Smallness” was determined by trial and error in choosing smaller and smaller “m” and “J”.
The final set of ODE then becomes,
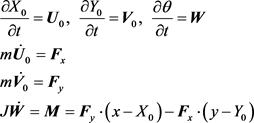 (13)
(13)
Force F and torque M on the object is calculated [22] for a body in slow motion with a known velocity and rotational rate.
At low Reynolds number flow, swimming motion of a small object depends on different wave parameters.
2.3. Model Description
2.3.1. Vertical Cylindrical Model Using RLT (Figure 3)
Consider the axial symmetric axis and the dynamic simulation of thin rigid fiber body, the force distribution is at zero Reynolds number with slow flow. The vertical cylindrical pressure force on the circular area is calculated by using Reynolds
![]()
Figure 3. Vertical model shape in COMSOL.
lubrication theory. In the minimum separation between particle and bottom wall tank, lubrication dominates the short-range interactions. This short-range hydrodynamic force is calculated using lubrication approximation. The lubrications formulas are derived by [37].
Suppose the fiber has a finite length, a short-range interaction between the fiber and fluid, the lubrication equations of [37] are implemented using a dimensional radius of curvature is equal to the particle length. For the vertical cylindrical case our Reynolds Lubrication Equation is
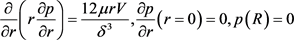
To solve the force distribution the pressure is derived in the fiber coordinates.
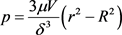
The far-field hydrodynamic interaction and the end interaction of thin fiber have no effect. However, the details must be included when calculating the lubrication interactions. The equations in Claeys and Brady [37] are handled in the same manner as above using the lubrication analysis. For the bottom wall tank interacting with a cylindrical body, the total pressure force on the circular area in z-direction becomes,
![]()
2.3.2. Spherical Model Using RLT (Figure 4)
The spherical model has a two-dimensional (2D) axi-symetric axis. The object is
![]()
Figure 4. Spherical model shape in COMSOL.
falling in an infinite tank filled with viscous fluid. The same boundary conditions (vertical cylindrical) have used for force and velocity calculation. The sphere in tank case has been used to assess the element mesh density necessary to obtain the force accurately and for sufficiently small radius to tank width ratio R⁄W can be compared to the Stokes force on a sphere in an infinite fluid.
The spherical polar coordinates are,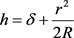 .
.
In addition, the Reynolds lubrication equation becomes,
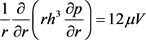
Pressure, 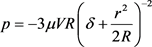 , and total force,
, and total force,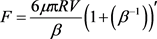 .
.
2.3.3. Moving Coordinates (Figure 5)
Consider the two-dimensional (2D) numerical simulations of Stokes flow for the small swimming object at low Reynolds number. We have chosen two reference frames, one is fixed (Global Coordinates), and another is the moving frames of reference (Local Coordinates). The local coordinates moves with fluid particle. This motion is realised when we apply the moving boundary condition on fluid particle. For the swimming object with moving mesh, we choose the 2D plane axis. For the moving mesh, we have allowed for re-meshing using the arbitrary Lagrangian-Eulerian (ALE) technique and have added Stokes equation from MEMS module in COMSOL Multiphysics software.
When we allow for re-meshing, we get three frames: The spatial frame, the reference frame, the mesh frame. The spatial frame coordinates are x and y by default, the reference frame coordinates are X and Y by default and the mesh frame coordinates are xm and ym by default. In the moving case, we have chosen
![]()
Figure 5. Picture of two frames where particle is moving with local frame.
a large tank that is filled by viscous fluid and elliptical object shape that is moving or swimming in the fluid. In Subdomain Setting we use free displacement which means mesh displacement is controlled only by the boundary conditions on the surrounding boundaries. In boundary setting we use two kinds of setting. For tank boundary we add mesh displacement module and in x and y direction add zero because our global coordinate is fixed and there is no mesh displacement in here, and for object boundary we add mesh velocity u and v, which is the free boundary.
3. Results and Discussion
3.1. Vertical Cylindrical Model
3.1.1. Velocity and Pressure Model (Figure 6)
There are some necessary steps to be taken to get a complete solution of vertical cylindrical model in COMSOL. Select geometry, constant parameters, set-up equation system, boundary conditions (applied at the global and subdomain level), and refine mesh or non-uniform mesh is to avoid error in solution between two bottom wall. One tries to choose different orders of elements for finite element solutions like the Lagrange quadratic or the Lagrange cubic. If the difference in solution between using quadratic or cubic elements is negligible, one can retain the lower order element. It is seen in this case that there is practically no difference between solutions arising from the choice of quadratic (2nd order) or cubic (3rd order) Lagrange shape functions. Hence, quadratic Lagrange elements are used. Finally, the solution is sought and then post processing is carried out to visualize the solution fields of interest.
The velocity and pressure plots are near the bottom wall of the tank. The pressure plots show some spikes at the cylinder edges. This is owing to the singularities that arise at sharp corners or edges of the cylinders [38]. An option to avoid singularity is to refine the meshes at these locations. This could be done either by increasing the order (p-convergence) or by increasing the number of elements (h-convergence). However, either of these options didn’t yield the result and one is led to think that the alternative would only be to smoothen out the sharp edges.
3.1.2. Force: Compare RLT with PDE (Figure 7)
The numerical (PDE) and the theoretical forces (LRT) are calculated, the x-axis corresponds to the ratio 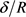 describing the motion of the cylinder towards the bottom wall of the tank and plotted the along y-coordinate are the forces on the cylinder calculated numerically and theoretically. The force grows quickly when
describing the motion of the cylinder towards the bottom wall of the tank and plotted the along y-coordinate are the forces on the cylinder calculated numerically and theoretically. The force grows quickly when 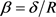 is below 0.05. For values of
is below 0.05. For values of 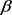 greater than this the value of force asymptotically approaches the value of zero (0).
greater than this the value of force asymptotically approaches the value of zero (0).
Logarithmic plots are used to find the differences in growth rates for the force in the numerical and the theoretical case. The logarithmic plot also shows that the force in the low ranges of  is proportional to
is proportional to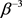 . The force plot seems to show a favorable agreement between the numerical and theoretical calculations
. The force plot seems to show a favorable agreement between the numerical and theoretical calculations
![]() (a)
(a) ![]() (b)
(b)
Figure 6. Vertical cylindrical coordinate system plot. (a) Velocity plot; (b) Pressure plot.
![]() (a)
(a)![]() (b)
(b)
Figure 7. Compare solution and loglog plot for vertical cylinder force calculation. (a) Compare solution; (b) Loglog plot.
for the vertical cylinder. It must however be kept in mind that we have introduced the slightly compressibility as opposed to the incompressibility that is otherwise assumed.
3.2. Spherical Model
3.2.1. Velocity and Pressure Model
Consider the sphere is close to the bottom wall boundary. The pressure field results shown in Figure 8(b) shows no spikes and this seems to indicate that the horizontal and spherical model are best used to avoid unsavoury spikes in the pressure fields.
3.2.2. Force: Compare RLT with PDE
The forces have been computed for the cases of sphere close to the bottom wall of the tank. We examine the force when the spherical model reaches near the bottom wall of the tank. The plots in Figure 9 seem to produce a good agreement for the force fields between the theoretical and the numerical simulations.
![]() (a)
(a) ![]() (b)
(b)
Figure 8. Velocity and Pressure plot of spherical model. (a) Velocity plot; (b) Pressure plot.
![]() (a)
(a)![]() (b)
(b)
Figure 9. Force and logarithmic plot of spherical model. (a) Force plot; (b) Loglog plot.
3.3. Swimming Object Simulation
We have focussed on visualizing the resultsfor swimming object, continuously re-meshingthe object to reach final time step. The geometry of deformations has shown at different time steps in Figure 10.
Figure 10 depicts the object in its wiggling motion starting from an initial shape and returning back to its initial shape in a certain time. The surface plots on the moving object depict the velocity at different time steps. The deformation of this object depends upon its boundary conditions. It is seen in the initial time step that the velocity at the edges of the moving object is the highest.
The linear and angular velocity for moving object is calculated on the basis that net force and torque on the object are zero. That means these forces are calculated from the global coordinate system and the velocities are applied on the moving object boundary. Using these conditions, allows one to visualise the motion of the object up till its final time step. The convergence of solution for each of the time step is rather slow and this results in a longer duration for the entire solution to be ready, sine one needs to re-mesh at every time step.
As opposed to the previous case, one sees in this Figure 11 that the object doesn’t come back to its initial shape. In every wiggling motion, one sees that the velocity is higher than the previous motion. It shows that that the deviation of the motion from an average straight line is sinusoidal in nature.
3.3.1. Mesh Displacement
The six different images of mesh displacement is at different time steps (Figure 12). The first image corresponds to a time step of t = 0. In this the mesh is equally distributed around the corners of the swimming object. However in the third, fourth and fifth images one can see the mesh in its deformed form. The object deformation is identical to the way the mesh has deformed. On the left hand side there is compression in the negative x-direction and the right mesh elements are stretched. The meshes in the first image are structured while the remaining meshes are seen to be unstructured.
3.3.2. Velocity Profile
Force and torque are applied on the moving object from the global coordinate system and we get the linear and angular velocity of local variables. The slow motion of the worm is noticed by the change in velocities or motion of the local co-ordinate system.
![]()
Figure 10. Periodic motion at different time steps. (a) t = 0.0 s; (b) t = 0.2 s; (c) t = 0.5 s; (d) t = 1.2 s; (e) t = 1.4 s; (f) t = 1.7 s; (g) t = 2 s; (h) t = 2.1 s.
![]()
Figure 11. Object swimming very slowly. (a) t = 0.2 s; (b) t = 0.6 s; (c) t = 5.5 s; (d) t = 7.7 s; (e) t = 8.7 s; (f) t = 10 s.
![]()
![]()
Figure 12. Mesh displacement at different time steps. (a) t = 0.0 s; (b) t = 0.2 s; (c) t = 0.6 s; (d) t = 1.1 s; (e) t = 1.5 s; (f) t = 2 s.
The result shows that the x-direction mean displacement profile for global coordinate system and its derivatives displacement with respect to time profile of same coordinates system. The x-direction displacement refers to the moving object displacement per time period.
Imagine the object to be an ellipsoid moving by combinations of horizontal wave pattern travelling from one place to another with small amplitude and wave length. By using a combination of such oscillations for the motion, the swimmer can move in the opposite direction to that of the surface waves [34].
Figure 13 is a plot of the fluid velocity field directions near the swimming object. Here we see that the domain velocity direction has changed periodically with the object motion, except that they would be translated in the direction of the object wave motion.
Velocity profile observation for different motion cases
It has already been stated that the body motion is periodic if amplitude of motion is small [24] [39]. It’s a good approximation for periodic motion of ellipsoid when amplitude and wave length are both small. We use identical idea to observe the mean velocity profile and mean displacement in a periodic motion of the ellipsoid body.
The periodic motion is observed for different amplitudes and wave length to see mean velocity profile for different waveforms. Results from the comparison of these with the calculated velocity profile are shown in below. Velocity profile amplitude ![]() and wave length
and wave length ![]() are default values in this observation. There seems to be a good agreement with the calculated values. The results are summarised in Table 1 below.
are default values in this observation. There seems to be a good agreement with the calculated values. The results are summarised in Table 1 below.
Observation:
From this velocity profile observation it is seen that the default mean displacement and mean velocity values agree very well. One, two and four time periods mean velocity values are almost the same implying that the wiggle motion is small and its moving very slowly in every period.
In the first observation, amplitude is reduced by 10% to ![]() and wave length remains fixed at
and wave length remains fixed at![]() . The x-direction mean velocity profile and mean displacement value are verified. They are almost identical to the mean velocity and mean displacement Figure 13 that are obtained in default calculation in Table 1.
. The x-direction mean velocity profile and mean displacement value are verified. They are almost identical to the mean velocity and mean displacement Figure 13 that are obtained in default calculation in Table 1.
![]()
Table 1. Different amplitude and wave length.
In second observation, the amplitude has been reduced by 50% to ![]() but wavelength remains fixed at
but wavelength remains fixed at![]() . This experiment results shows only for one and two time periods respectively. But the fourth time period motion could not be obtained with consistent initial values.
. This experiment results shows only for one and two time periods respectively. But the fourth time period motion could not be obtained with consistent initial values.
This simulation result is less efficient from the first observation mean velocity result and the mean velocity value decreases at small amplitudes. But at amplitude below 0.003 then there is an error suggesting a failure to find consistent initial values. In the third observation, we take the default amplitude value, ![]() and increase 75% the wave length to
and increase 75% the wave length to![]() . One gets inefficient wiggling at the change of wave length alone and when the mean velocity value is very small. When we increase wave length over 1.5 then the solvers returns an error.
. One gets inefficient wiggling at the change of wave length alone and when the mean velocity value is very small. When we increase wave length over 1.5 then the solvers returns an error.
In fourth observation, we choose a smaller value for amplitude, ![]() and a larger value for wavelength
and a larger value for wavelength![]() . The velocity profiles remain insufficient and the mean displacement and mean velocity of wiggling object is not smooth. In this case we have changed both wave length and amplitude, and it is seen that in every period of this observation mean velocity value is very smaller than previous observations.
. The velocity profiles remain insufficient and the mean displacement and mean velocity of wiggling object is not smooth. In this case we have changed both wave length and amplitude, and it is seen that in every period of this observation mean velocity value is very smaller than previous observations.
4. Summary and Conclusions
In this study, we have developed low Reynolds number flow to simulate the effect of a thin fibre falling in a tank filled with viscous fluid. This allows for the observation and calculation of the forces exerted by the fluid on the thin fibre. Slightly compressible assumption is imposed upon the incompressible Stokes flow equation. It was observed that there needs to be an increased refinement of the meshes as the falling objects approach the bottom boundary of the tank. Simulations provide the velocity, pressure and force on the body. Reynolds Lubrication theory is used to theoretically model the problem while the numerical solution is sought in COMSOL, and compared the results obtained from calculations and it showed a good agreement.
The second model focuses on object moving with a moving mesh and emphasised on the velocity for the swimmer object. Choose two coordinate systems: one is fixed and another is moving with rotation and translation. The fluid-flow simulation in a moving coordinate system is coupled to an ordinary differential equation (ODE) describing the object motion. The idea that the net force and torque exerted by the surrounding fluid on the object are zero is used to calculate the unknown linear and angular velocity. Re-meshing is used for moving boundary objects. The simulations show velocity and mesh displacement profiles. The velocity profiles that we got for the case of moving objects agreed with our anticipations.
For velocity observations, we compute the table for ![]() and
and ![]() and have seen that mean velocity is equivalent to the amplitude (i.e.,
and have seen that mean velocity is equivalent to the amplitude (i.e.,![]() ) and for the efficient swimming of small objects, it is seen that wave length should be smaller than the size of the moving object (i.e.,
) and for the efficient swimming of small objects, it is seen that wave length should be smaller than the size of the moving object (i.e.,![]() ). The development methods in COMSOL 3.5 Multiphysics with Matlab has worked sufficiently well in getting a good enough solution as required in our study.
). The development methods in COMSOL 3.5 Multiphysics with Matlab has worked sufficiently well in getting a good enough solution as required in our study.
Acknowledgements
I am grateful to my colleague and friends who supported me to finish the work.