1. Introduction
Logistic regression is a proper analysis method to model the data and explain the relationship between the binary response variable and explanatory variables. The maximum likelihood estimator is a common technique of parameter estimation in the binary regression model. Unfortunately, this method does not resistant against atypical observations in data. To handle this problem, many robust estimators an alternative to MLE have been proposed. [1] developed a diagnostic measurement of outlying observations and they showed that in the logistic regression, the MLE was very sensitively to outlying observations (see also [2]). [3] discussed different types of M-estimators for binary regression, these estimates belong to the Mallows-type based on leverage down weight. [4] derived a robust estimator based on a modified median estimator for the logistic regression model and they also studied a Wald-type test statistic for the logistic regression model. [5] developed projection estimators for the GLM which are very robust but their computation is extremely complex. [6] defined a robust estimator based on the quasi-likelihood, which replaced the least squares estimator (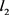 norm) by the least absolute deviation estimator (
norm) by the least absolute deviation estimator ( norm) in the definition of quasi-likelihood. [7] proposed a natural class of robust estimator and testing procedures for binomial models and Poisson models, which are based on a concept of quasi-likelihood estimator proposed by [8]. [9] studied the breakdown of the maximum likelihood estimator in the logistic model. [10] suggested a highly robust and consistent estimator. [11] presented a stable and fast algorithm to compute the M-estimator introduced by [10]. [12] introduced a fast algorithm based on breakdown points of the trimmed likelihood for the generalized linear model. Another class of the robust estimator is the fisher-consistent estimators proposed by [10]. [14] studied a robust resistant estimator and this estimator based on the misclassification model. [15] generalized optimally bounded score functions studied by [16] for linear models to the logistic model.
norm) in the definition of quasi-likelihood. [7] proposed a natural class of robust estimator and testing procedures for binomial models and Poisson models, which are based on a concept of quasi-likelihood estimator proposed by [8]. [9] studied the breakdown of the maximum likelihood estimator in the logistic model. [10] suggested a highly robust and consistent estimator. [11] presented a stable and fast algorithm to compute the M-estimator introduced by [10]. [12] introduced a fast algorithm based on breakdown points of the trimmed likelihood for the generalized linear model. Another class of the robust estimator is the fisher-consistent estimators proposed by [10]. [14] studied a robust resistant estimator and this estimator based on the misclassification model. [15] generalized optimally bounded score functions studied by [16] for linear models to the logistic model.
In this article we investigate the use of weight functions introduced by [17] as a weight function for Mallows type (weighted maximum likelihood estimator) to obtain a robust estimation for logistic regression, in addition, to compare their performance with classical maximum likelihood estimator and some existing robust methods by means of simulation study and real data sets.
The maximum likelihood estimator for the logistic regression model is given in Section 2. In Section 3, we state a review and describe some of the existing robust techniques. We explain the performance of the estimators based on the results of a simulation study and real data in Section 4. The conclusion is given in Section 5.
2. Maximum Likelihood of Logistic Regression
Suppose the binary response variable 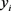 takes values (0,1), these numerical values represented the negative response and the positive response respectively. The mean of this variable will be the proportion of positive responses. If p is the proportion of the observations with an outcome of 1, then
takes values (0,1), these numerical values represented the negative response and the positive response respectively. The mean of this variable will be the proportion of positive responses. If p is the proportion of the observations with an outcome of 1, then  is the probability of an outcome of 0. The predictor variables
is the probability of an outcome of 0. The predictor variables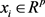 ,
, 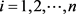 , the probability of positive response variable
, the probability of positive response variable 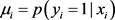 is linked to predictor variables by the mean of a link function
is linked to predictor variables by the mean of a link function , such that
, such that 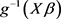 is the logit link function which transforms the covariate values in the interval (0,1).
is the logit link function which transforms the covariate values in the interval (0,1).
We can write the multiple logistic regression model by:
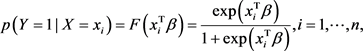 (1)
(1)
where  are the values of the predictor variables and
are the values of the predictor variables and 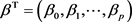 is the vector of unknown parameters. The binary regression model can be defined by:
is the vector of unknown parameters. The binary regression model can be defined by:
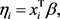
where 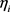 is a linear predictor and also known as transformation function, where
is a linear predictor and also known as transformation function, where 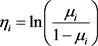 this transformation is known as a logit link function. There are another two transformation functions used in practice for modeling binomial and Bernoulli data:
this transformation is known as a logit link function. There are another two transformation functions used in practice for modeling binomial and Bernoulli data:
• The probit function ,
,
• The complementary log-log function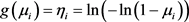 .
.
In this article, we focus on a logit function as a link function. The classical maximum likelihood estimator is used to estimating the vector of unknown parameters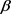 . Suppose that the response variables
. Suppose that the response variables ![]() distributed according to the Bernoulli distribution and the probability distribution for the ith observation is given by:
distributed according to the Bernoulli distribution and the probability distribution for the ith observation is given by:
![]()
and each observation ![]() takes the value 1 with probability
takes the value 1 with probability ![]() or the value 0 with probability (
or the value 0 with probability (![]() ). The likelihood function is given by:
). The likelihood function is given by:
![]() (2)
(2)
then, we take a log-likelihood of above formula:
![]()
where ![]() and
and![]() , then, the log-likelihood can be written as:
, then, the log-likelihood can be written as:
![]() (3)
(3)
In design experiments, we have repeated observations or trials at each level of the explanatory variables (x). Let ![]() be a number of the trials at each level of the predictor and
be a number of the trials at each level of the predictor and ![]() be the number of 1’s observed at the ith observations with
be the number of 1’s observed at the ith observations with![]() . Then, the log-likelihood is given by:
. Then, the log-likelihood is given by:
![]() (4)
(4)
however, the likelihood function can be maximized by differentiating it with respect to![]() :
:
![]()
where, ![]() , we have
, we have
![]()
where![]() , represents the mean of the binomial variable, we can write above equation in matrix notation as
, represents the mean of the binomial variable, we can write above equation in matrix notation as![]() , where
, where
![]()
As a result, the MLE estimator is typically done by solving the score equation:
![]() (5)
(5)
Equation (5) is nonlinear in ![]() one may use the iteratively weighted least squares (IWLS) algorithm. The method of iteratively weighted least squares is used to solve certain optimization problems, in logistic regression model the (IWLS) is used to find the maximum likelihood estimates with objective function of the form of:
one may use the iteratively weighted least squares (IWLS) algorithm. The method of iteratively weighted least squares is used to solve certain optimization problems, in logistic regression model the (IWLS) is used to find the maximum likelihood estimates with objective function of the form of:
![]() (6)
(6)
by an iterative method in which each step involves solving a weighted least squares problems of the form:
![]()
where ![]() is the diagonal matrix of weights, usually will all elements set initially to
is the diagonal matrix of weights, usually will all elements set initially to![]() . Let use rewrite
. Let use rewrite ![]() as a matrix form:
as a matrix form:
![]()
where ![]() is the vector of linear predictor
is the vector of linear predictor![]() , in the other hand the Newoton method can be factorized as:
, in the other hand the Newoton method can be factorized as:
![]()
with a new vector![]() . That is
. That is ![]() is the solution of a weighted least square problem with weight
is the solution of a weighted least square problem with weight![]() , response vector
, response vector ![]() and explanatory variable
and explanatory variable![]() .
.
3. Robust Estimators in Logistic Regression
An outlier is an observation deviated from the other values in data and produces the large residuals. In the logistic regression model, an outlier can be occurred in the response variables as well as in the predictor variables or in both. In the binary regression model, all the response variables ![]() are binary, takes the numerical values 0 or 1, therefore, an outlier in the response variable can only occur as a transposition
are binary, takes the numerical values 0 or 1, therefore, an outlier in the response variable can only occur as a transposition ![]() or
or ![]() discussed by [14]. An error in response variables is also well-known as a misclassification error or residual outlier. Extreme observation in explanatory variables is known as a leverage point or leverage outlier: there are two types of leverage point, good and bad. A good leverage point occurs when
discussed by [14]. An error in response variables is also well-known as a misclassification error or residual outlier. Extreme observation in explanatory variables is known as a leverage point or leverage outlier: there are two types of leverage point, good and bad. A good leverage point occurs when ![]() with a small value of
with a small value of ![]() or when
or when ![]() with a large value of
with a large value of![]() , and vice versa for a bad leverage point. The classical maximum likelihood estimation can be influenced by leverage points and misclassification in the response variables, studied by [13] and [14]. To solve this problem, there are many robust estimators proposed for GLM, specifically, for the logistic and Poisson models. For instance, the Mallows-type technique of [2] and we can also cite works of ( [2] [3] [7] [10] [13]).
, and vice versa for a bad leverage point. The classical maximum likelihood estimation can be influenced by leverage points and misclassification in the response variables, studied by [13] and [14]. To solve this problem, there are many robust estimators proposed for GLM, specifically, for the logistic and Poisson models. For instance, the Mallows-type technique of [2] and we can also cite works of ( [2] [3] [7] [10] [13]).
In this article we proposed a new class of robust techniques for logistic regression, they are weighted maximum likelihood estimators, where the weight depends on the weight functions introduced by [17] as a weight of explanatory variables in Mallows-type estimator. In addition, we compare the performance of these techniques with classical maximum likelihood, Mallows-type estimator and unbiased bounded-influence estimator, in the presence of outliers.
3.1. Conditionally Unbiased Bounded-Influence Estimator (CUBIF)
In the CUBIF estimator, the weights of controlling atypical observations depend on the response variables and the predictor variables, this estimator is also known as the Schweppe class estimator introduced by [2]. The idea of this method is to minimize a measure of efficiency based on the asymptotic variance-covariance matrix to bound the measure of infinitesimal sensitivity. The M-estimators are the solution of the form of![]() , such that
, such that![]() , where
, where ![]() represents the ith response variable,
represents the ith response variable, ![]() represents the ith explanatory variables,
represents the ith explanatory variables, ![]() is a vector of unknown parameters and
is a vector of unknown parameters and ![]() is a known
is a known ![]() functions that does not depend on i or n. We can write the optimal function of
functions that does not depend on i or n. We can write the optimal function of ![]() as follows:
as follows:
![]() (7)
(7)
where B is a variance covariance matrix, b is bounded on the measure of infinitesimal sensitively and ![]() is a leverage measure. The function
is a leverage measure. The function ![]() is a bias correction term with corrected residual given by:
is a bias correction term with corrected residual given by:
![]() (8)
(8)
The weights function in the form of![]() , where
, where ![]() represent the Huber weights function given by
represent the Huber weights function given by![]() . The weight function W downweights observations with a high leverage point and large corrected residual making M-estimator to have bonded influence.
. The weight function W downweights observations with a high leverage point and large corrected residual making M-estimator to have bonded influence.
3.2. Mallows Type Class (Mallows)
[2] proposed Mallows-type leverage dependent weight estimator, this estimator minimizes the weighted log-likelihood function, where the weight depends on the explanatory variables. [3] discussed more deeply on Mallows-type estimator and suggested a simple way to make the maximum likelihood estimator more robust by downweighting the atypical observation in the predictor variables. The leverage of observation x can be measured by the following:
![]() (9)
(9)
where ![]() represents a robust location estimator, and
represents a robust location estimator, and ![]() represents a robust variance-covariance matrix of the continuous covariates (
represents a robust variance-covariance matrix of the continuous covariates (![]() ). The initial robust scale and location estimator of continuous
). The initial robust scale and location estimator of continuous ![]() and
and![]() , can be calculated by using minimum covariance determinant (MCD) approach. The Mallows type estimator for logistic regression can be obtained by a solution of the form of:
, can be calculated by using minimum covariance determinant (MCD) approach. The Mallows type estimator for logistic regression can be obtained by a solution of the form of:
![]() (10)
(10)
where![]() , W is a non-increasing function such that
, W is a non-increasing function such that ![]() is bounded. [3] suggested choosing W depends on a constant
is bounded. [3] suggested choosing W depends on a constant![]() .
.
![]()
this estimate is called the weighted maximum likelihood estimate (Mallows-type estimator) and the influence function of WMLE is given by:
![]() (11)
(11)
where ![]() with
with ![]() and
and ![]() are the limit values of
are the limit values of ![]() and
and ![]() and
and
![]() .
.
3.3. Weighted Maximum Likelihood Estimator (WMLE)
Similar to the strategy used in constructing the Mallows-type estimator, we proposed a new class of robust techniques, they are the weighted maximum likelihood estimators, with weight depends on the weight functions introduced by [17]. First, compute the initial location and scatter estimators of the explanatory variables ![]() and
and ![]() respectively. Then, calculate the squared Mahalanobis distances of the explanatory variables which can be defined as:
respectively. Then, calculate the squared Mahalanobis distances of the explanatory variables which can be defined as:
![]()
The weight function we proposed can be defined as: first weight: ![]() , where
, where ![]() refers to squares Mahalanobis distances, then:
refers to squares Mahalanobis distances, then:
![]()
second weight:![]() , then, we can write in the form of:
, then, we can write in the form of:
![]()
Then, the weighted maximum likelihood estimators for logistic regression can be obtained by a solution of the form of:
![]() (12)
(12)
For these weights no observation is trimmed we used the modified algorithm for Mallows-type estimator of [3] for computation of the weighted maximum likelihood estimates.
4. Evaluation of the Robust Estimators
In order to examine the performance of the estimators, two approaches have been taken. The first includes simulated models for comparing the new techniques with the classical MLE, Mallows type estimator for [2] and [3]. In the second, we used real data sets of leukemia data.
4.1. Simulation Study
In this subsection, a simulation study was carried out to examine the performance of new robust techniques (WMLEw1, WMLEw2) and compare with MLE, conditionally unbiased bounded influence (CUBI) of [2] and the Mallows-type estimator (Mallows) of [3]. The weighted maximum likelihood estimator was computed using the modified algorithm for Mallows type estimator. The Mallows and CUBI were computed by the standard available in the robust package of R. The simulation study involves four models, these are an uncontaminated model (model 1), 5% of the data are contaminated (model 2), 10% moderate contaminated (model 3) and 20% extreme contaminated model (model 4). In the first scenario without contamination, we generated two predictor variables according to the standard normal distribution with mean zero and variance one, ![]() and
and![]() , with four sample sizes,
, with four sample sizes,![]() . The large sample size was selected to guarantee the existence of the overlapping in each replication. The response variable is generated from the Bernoulli distribution with parameter equal to
. The large sample size was selected to guarantee the existence of the overlapping in each replication. The response variable is generated from the Bernoulli distribution with parameter equal to![]() . The true parameters for the clean model setting as
. The true parameters for the clean model setting as![]() . In the second scenario, 5% of the data are contaminated with the amount of deviating atypical observation in the x-direction is taken as
. In the second scenario, 5% of the data are contaminated with the amount of deviating atypical observation in the x-direction is taken as![]() , the vector of true parameter for contaminated observations equals
, the vector of true parameter for contaminated observations equals![]() . The predictor variables for contaminated models were generated according to normal distribution,
. The predictor variables for contaminated models were generated according to normal distribution, ![]() and
and![]() . The third and four models are in the same way as the second scenario with a percentage of contamination equals 10% and 20% respectively and a quantity of deviating atypical observation in the x-direction equals (5). The new values of the predictor variables are denoted by
. The third and four models are in the same way as the second scenario with a percentage of contamination equals 10% and 20% respectively and a quantity of deviating atypical observation in the x-direction equals (5). The new values of the predictor variables are denoted by ![]() and
and![]() , where the response variable
, where the response variable ![]() for the contaminated model are generated from the following model equations:
for the contaminated model are generated from the following model equations:
![]() (13)
(13)
The performance of these estimators is examined based on the Bias and mean squared error (MSE) for different scenarios. However, the estimator which has small Bias and MSE is a good one. In each scenario run included over 1000 repetitions. Therefore, the bias and mean squared error for each parameter are computed as follows:
![]()
and
![]()
4.2. Results from the Monte Carlo Simulation Study
Table 1 reports bias and mean squared errors of the five estimators for the contaminated data. The results indicate that the bias and MSE of MLE, Mallows, CUBIF estimators are fairly close to each other, both WMLEw1 and WMLEw2 estimators perform less compared to other estimators. It can observe that the bias and mean squared errors decrease when the sample size is increased. As can be seen from Table 2 under 5% of the data was contaminated, the two new robust techniques WMLEw1 and WMLEw2 have overall the best performance among all compared estimators for different sample sizes.
The results of moderate in Table 3 with 10% of the data are contaminated and extreme bad leverage point in Table 4 with 20% of the data are contaminated demonstrated that our weighted maximum likelihood estimators WMLEw1 and WMLEw2 perform better than other estimators in the term of bias and mean squared errors. However, the classical maximum likelihood estimates perform poorly in the contaminated model due to the sensitivity of outliers. In summary, the two new estimators show the best performance among all compared techniques in contaminated data. Moreover, these new estimators have reasonable perform in clean data.
![]()
Table 1. Bias and mean squared errors of estimators for model 1.
![]()
Table 2. Bias and mean squared errors of estimators for model 2.
![]()
Table 3. Bias and mean squared errors of estimators for model 3.
![]()
Table 4. Bias and mean squared errors of estimators for model 4.
4.3. Leukemia Data
The datasets analyzed here. This data includes 33 leukemia patients. Three variables were measured for each patient: Time, AG and WBC. The response variable is a survival time patient in weeks, we coded into (1 = the patient survived more than 52 weeks, 0 = otherwise). The two explanatory variables are: WBC measured a white blood cell count of patient and AG is a binary variable (1 = present of morphologic characteristic of white blood cells, 0 = absent of morphologic characteristic of white blood cells) according to an identification method of atypical observation in the leukemia data, the observation number 17 looks like atypical. A logistic regression model was fitted using binary survival time y as the response variable and AG and WBC as the predictor variables. The estimators examined here are new weighted maximum likelihood estimates (WMLEw1, WMLEw2), MLE, MLE17 (MLE17 is the maximum likelihood estimator for clean data after excluding observation number 17), Mallows (Mallows type estimator) and CUBIF (conditionally unbiased bounded-influence function estimator).
It can be observed from Table 5, the MLE is very sensitively to influential observations. In addition, after deleting observation number 17 reduced the effect of WBC close to zero. The new WMLE estimators (WMLEw1, WMLEw2) are showed the best performance among all other estimators for the leukemia data. However, Mallows estimates are sensibly close to the MLE17.
5. Conclusion
In this study, we introduced two new robust techniques of logistic regression, also known as weighted maximum likelihood estimators. In order to examine the performance of new techniques, we conducted simulation experiments under different scenarios and real datasets. The classical maximum likelihood estimates show the lack of robustness when outliers are present. Our simulation experiments for uncontaminated models demonstrated that the MLE, Mallows and CUBIF estimators are fairly perform close to each other, while, the new weighted techniques perform less compared to other estimators. In both simulation study under different contaminated scenarios and real datasets, the new proposed weighted maximum likelihood techniques showed the best performance among all compared estimators. The new techniques used here to construct robust estimators can also be extension to other generalized linear models like Poisson regression model and negative binomial model.
![]()
Table 5. The estimated parameters and standard errors for the leukemia data.