Contact Pressure between the Outside Surface of the Sealer and Cylinder Wall ()
1. Introduction
Achieving tightness with the least external load by sealers improves their efficiency and determination of sealing parameters has an important scientific value [1] - [9]. A major problem with these studies arises from the ignoring influence of edge effects and heredity and also, mechanism of achieving tightness was not studied enough. The mechanism of achieving tightness was touched upon in the works [1] [2] [3]. As the experience of using sealing elements shows, the edge effects and heredity have a significant influence on their sealing ability [10] [11] [12] [13]. Therefore, study of sealing ability of cylindrical sealing elements with regard to edge effects and heredity and development on this basis effective measure to improve their efficiency has both a practical and scientific value.
In this paper, based on theoretical investigations, we determine the character of contact pressure distribution between the outside surface of the sealing element and rigid cylinder wall depending on geometrical sizes and mechanical properties of the sealer under its unilateral compression.
The magnitude of the axial load for achieving tightness with regard to differences of strain state before and after contact of outside surface of the sealing element with cylinder wall, is defined. The dependence between the magnitude of the axial load necessary for tightness and geometrical sizes under unilateral compression of the sealing element, is established. It is shown that with decrease in the height of the sealing element the axial load necessary for achieving tightness, greatly increases. Furthermore, the limiting value of the height of the sealing element under unilateral compression, above which contact pressure depends a little on the magnitude of the axial load, is defined.
In this paper, the first section is exposed to research background of this paper’s work and the structure of this paper. Section 2 introduces the elastic statement of problem, and the dependence between the axial load necessary for the first contact of the outer surface of the sealing element with the rigid cylinder wall and its physic-mechanical properties and geometrical sizes is established. In Section 3, the analytic formula allowing to determine the axial load necessary for full contact and tightness of the surface of the sealing element and cylinder wall depending on its physic-mechanical properties and geometrical sizes is found. Section 4 introduces the character of contract pressure distribution between the outside surface of the sealing material and rigid cylinder wall depending on geometrical sizes and mechanical properties of a sealer under its unilateral compression. In Section 5, based on linear laws of heredity the influence of viscous-elastic properties of the cylindrical sealing element on its sealing ability is determined. In Section 6, numerical calculations are conducted under different conditions, and the results of numerical calculations are represented in the form of graphs of contact pressure and external forces necessary achieving sightless and discussed. In Section 7, some conclusions are reached.
2. Statement and Solution of the Problem Elastic Solution
First, some parameters are given in Table 1.
Let us consider a sealing element tightly put on the stock and with a gap 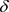 between its outside surface and rigid cylinder wall (Figure 1).
between its outside surface and rigid cylinder wall (Figure 1).
The tightness of the surface of the sealing element and cylinder wall is achieved by unilateral axial compression (Figure 1). The solution of the problem is performed in two stages. The first step is compression of the sealing element to the first contact of its outside surface with cylinder wall, the second state is to achieve tightness.
Let us consider the first stage. As the material of the sealing element is homogeneous, we accept its deformation as axially-symmetric. Then we can use the hypothesis of plane sections and assuming that the axial deformation of the sealing element depends only on the coordinate z in the axial direction.
We locate the origin of the coordinate system in the center of the lower section of the sealing element, direct the coordinate axis z vertically-upwards, the axis r to the direction of increasing the radius (see Figure 1).
Allowing for above assumptions, we accept the deformation of the sealing element 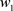 in the axial direction in the form [1] [2] [3]
in the axial direction in the form [1] [2] [3]
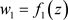 , (2.1)
, (2.1)
where 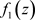 is an unknown function dependent on z and to be determined.
is an unknown function dependent on z and to be determined.
Accepting the sealing element material as incompressible [3] [14] we have the equality
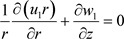 , (2.2)
, (2.2)
where  is deformation of the sealing element in the radial direction.
is deformation of the sealing element in the radial direction.
Allowing for formula (2.1), from expression (2.1) we get
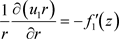 . (2.3)
. (2.3)
Integrating expression (2.3), we have the equality
 , (2.4)
, (2.4)
where 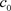 is an integration constant.
is an integration constant.
The boundary condition has the form:
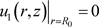 . (2.5)
. (2.5)
Then, allowing for condition (2.5), from expression (2.4) we get
 . (2.6)
. (2.6)
For the potential energy of the sealing element, after its deformation with regard to axisymmetry, we have the equality [3] [6]
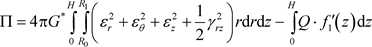 , (2.7)
, (2.7)
where H is height;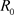 ,
, 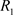 are inner and outer radii of the sealer;
are inner and outer radii of the sealer; ,
, 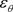 ,
, ![]() and
and ![]() are radial, tangential, axial and shear deformations, respectively [5] [14] :
are radial, tangential, axial and shear deformations, respectively [5] [14] :
![]() ;
;![]() ;
;![]() ;
;![]() . (2.8)
. (2.8)
Then allowing for formulas (2.1), (2.6) and (2.8), from expression (2.7) we get
![]() (2.9)
(2.9)
where G is a shear modulus of the sealing material.
Based on the Euler equation [15] [16] from the functional (2.9) we have
![]() , (2.10)
, (2.10)
where![]() ,
,![]() .
.
Integrating differential Equation (2.10) accepting![]() , we get the equation
, we get the equation
![]() (2.11)
(2.11)
![]() .
.
![]() ,
, ![]() ,
, ![]() are integration constants determined from the boundary conditions
are integration constants determined from the boundary conditions
![]() ;
;![]() ;
;![]() , (2.12)
, (2.12)
where ![]() is a friction coefficient between the washer and the end of the sealer.
is a friction coefficient between the washer and the end of the sealer.
Allowing for boundary conditions (2.12), from the expression (2.11) we get
![]() ;
;![]() ;
;
![]() (2.13)
(2.13)
![]() .
.
The radial stress at any point of the sealer, with regard to its compressibility can be defined by the formula [3] [14] [17]
![]() , (2.14)
, (2.14)
where s is a hydrostatic pressure function.
s can be determined from the boundary condition
![]()
![]() . (2.15)
. (2.15)
Then, allowing for expression (2.6) and (2.14), from condition (2.15) we get
![]() . (2.16)
. (2.16)
We define the axial load Q for repressing the scalar by the formula
![]() , (2.17)
, (2.17)
on the other hand, we have the equality
![]() . (2.18)
. (2.18)
Allowing for expressions (2.11), (2.13)-(2.16) and (2.18), from expression (2.17) we get
![]() . (2.19)
. (2.19)
From expression (2.19) we define q in the explicit form
![]() (2.20)
(2.20)
![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
3. Determining Axial Load until the Outer Surface of the Seal Is Completely in Contact with the Cylinder Wall
Now let us define the magnitude of the axial load necessary for complete contact of the outer surface of the sealing element with rigid cylinder wall. We locate the origin of the coordinate system at the center of the lower section of the sealing element and direct the axis z vertically upwards, the axis r to the side increasing of the radius as was shown in Figure 2.
Using the hypothesis of plane sections and assuming that the axial deformation of the sealing element depends only on the coordinate in the axial direction z, we can accept
![]() , (3.1)
, (3.1)
where ![]() is axial deformation of sections of the sealing element,
is axial deformation of sections of the sealing element, ![]() is an unknown function dependent only on z.
is an unknown function dependent only on z.
Then allowing for formula (3.1), from the incompressibility condition (2.2) we have
![]() , (3.2)
, (3.2)
where ![]() is an integration constant.
is an integration constant.
The boundary condition has the form
![]() . (3.3)
. (3.3)
Then allowing for the boundary condition, from expression (3.2) we get
![]() . (3.4)
. (3.4)
For the potential energy of the sealing element, after its deformation, with regard to axisymmetry of the problem we have the equality [9] [18].
![]() ,
,![]() . (3.5)
. (3.5)
Substituting expression (3.4) in formula (2.8), the obtained results in expression (3.5) and then integrating it with respect to r , based on the Euler equation [15] from the obtained functional we obtain the equality
![]() (3.6)
(3.6)
![]() ,
,
![]() .
.
The solution of differential Equation (3.6) will have the form
![]() , (3.7)
, (3.7)
where ![]() and
and ![]() are integration constants.
are integration constants.
Allowing for ![]() from expression (3.7) we get
from expression (3.7) we get
![]() . (3.8)
. (3.8)
We define the integration constants![]() ,
, ![]() and
and ![]() from the boundary conditions
from the boundary conditions
![]() ; (3.9)
; (3.9)
![]() ; (3.10)
; (3.10)
![]() ; (3.11)
; (3.11)
![]() .
.
Then allowing for boundary conditions (3.9)-(3.11), from expression (3.8) we have
![]() ;
;
![]() ;
; ![]()
![]() .
.
The axial force, necessary for deformation of the sealing element to its complete contact of its outer surface with cylinder wall, can be determined by the formulas
![]() , (3.12)
, (3.12)
where ![]() is axial stress in any cross section of the scaling element.
is axial stress in any cross section of the scaling element.
After complete contact of the outer surface of the sealing element with rigid cylinder wall, the boundary condition in the upper section has the form
![]() . (3.13)
. (3.13)
Then allowing for boundary condition (3.13), from expression (2.14) we get
![]() , (3.14)
, (3.14)
And allowing for expressions (2.18) and (3.14) the expression (3.12) takes the form
![]() . (3.15)
. (3.15)
Then allowing for formula (3.8), and expressions of![]() ,
, ![]() and
and ![]() from expression (3.15) we get
from expression (3.15) we get
![]() . (3.16)
. (3.16)
4. Contact Pressure between the Surface of the Sealer and Cylinder Wall
The contact pressure between the outside surface of the sealing element and cylinder wall after their complete contact can be determined (by the analogy with a beam on an elastic foundation) by the formula
![]() (4.1)
(4.1)
![]() .
.
If this time the tightness of the wall is not provided, then we continue to compress the sealing element. To determine the stress-strain state, at the distance z from the lower basis of the sealer we distinguish an annular element of height dz and compose for it the equilibrium equation
![]() , (4.2)
, (4.2)
where ![]() is tangential stress.
is tangential stress.
On the other hand, with regard to incompressibility of the sealing material, we have [2] [3]
![]() , (4.3)
, (4.3)
where ![]() is a friction coefficient,
is a friction coefficient, ![]() is Poisson’s ratio.
is Poisson’s ratio.
Substituting the expression (4.3) in Equation (4.2) and having integrated the obtained expression with regard to the boundary condition![]() , we get
, we get
![]() , (4.4)
, (4.4)
where ![]() is axial stress in the section of the sealing element, where the compression force is applied.
is axial stress in the section of the sealing element, where the compression force is applied.
The contact pressure distribution between the outer surface of the sealer and rigid cylinder wall can be determined from the expression (4.1) and (4.4) as follows:
![]() . (4.5)
. (4.5)
Then allowing for formula (4.4), from the expression (4.5) we get
![]() . (4.6)
. (4.6)
The value of ![]() maybe determined from the tightness condition
maybe determined from the tightness condition
![]()
![]() .
.
5. Heredity Accounting
Accounting of viscous-elastic properties of the material of the sealing element on sealing ability may be realized based on the hypothesis of elastic analogy [3] [13]. By this hypothesis when passing from elastic calculation to viscous-elastic one, only dependence between the stresses and strains changes.
It should be noted that at elastic analogy, all stress components satisfy the dependence between stresses and strain obtained on the basis of the chosen model for a uniaxial stress-strain state.
The dependence between the stress-strain components for an arbitrary case of loading of a model that describes best the viscoelastic behavior of the material of a sealing element, is of the form [3] [10] [11]
![]() , (5.1)
, (5.1)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() is dynamical viscosity of the material
is dynamical viscosity of the material
of the sealing element, ![]() is instantaneous modulus of elasticity,
is instantaneous modulus of elasticity, ![]() is an elasticity modulus,
is an elasticity modulus, ![]() are stress components,
are stress components, ![]() are relative strain components,
are relative strain components, ![]() is Kronecker’s symbol,
is Kronecker’s symbol, ![]() and
and ![]() is a time derivative from stress and strain components.
is a time derivative from stress and strain components.
Based on elastic analogy we represent
![]() . (5.2)
. (5.2)
Substituting expression (5.2) in formula (5.1), we get
![]() . (5.3)
. (5.3)
Integrating expression (4.3) with the initial condition ![]() we get
we get
![]() . (5.4)
. (5.4)
Introducing the denotation
![]() , (5.5)
, (5.5)
we can represent the expression (5.4) in the form
![]() . (5.6)
. (5.6)
For the considered case, when the sealing element at initial moment of deformation![]() .
.
![]() ,
,![]() . (5.7)
. (5.7)
Then allowing for (5.7), from expression (5.5) we get
![]() . (5.8)
. (5.8)
Allowing for the expression (5.8), from the expression (2.20) we get
![]() (5.9)
(5.9)
Allowing for the expression (5.8), from the expression (3.16) we get
![]() . (5.10)
. (5.10)
We now consider the case when the sealing element deforms uniformly. Based on the elastic analogy [3] [13] accepting the deformation of cross sections of the sealer in the form (Figure 3)
![]() , (5.11)
, (5.11)
![]() , (5.12)
, (5.12)
where ![]() is a Heaviside function,
is a Heaviside function, ![]() is time of deformation of the upper section of the sealing element to its first contact of the outer surface with the rigid cylinder wall.
is time of deformation of the upper section of the sealing element to its first contact of the outer surface with the rigid cylinder wall.
![]()
Figure 3. Graph of time dependence of relative axial deformation of the upper section.
From formulas (5.5) and (5.12) we get
![]() (5.13)
(5.13)
where ![]() is Dirac’s function.
is Dirac’s function.
Integrating formula (5.13), we get
![]() (5.14)
(5.14)
Then, allowing for formula (5.14) following from the expression (2.20) we get
![]() (5.15)
(5.15)
From the expression (5.15) we define the magnitude of the axial load necessary for recompressing the sealing element to contact of its outer surface with the cylinder wall.
Substituting formulas (5.14) in expression (3.16) for the axial load necessary for full contact of the outer surface of the sealing element with the cylinder wall with regard to heredity, we get
![]()
The axial load necessary for achieving tightness
![]() . (5.17)
. (5.17)
6. Numerical Calculation
Thus, based on theoretical investigations, the analytic formulas allowing to determine the contact pressure between the outside surface of the sealing element and rigid cylinder wall and the axial loads necessary for first and full contact of these surfaces depending on its physic-mechanical properties and geometrical sizes is found.
The numerical calculation is made by formulas (2.20), (3.16), (4.6), (5.9), (5.10), (5.15) and (5.16) for the values of parameters, which are showed in Table 2.
The results of numerical calculations are represented in the form of graphs of contact pressure and external forces necessary achieving sightless (Figures 4-10).
As is seen from Figure 4, with increasing the element’s height, the axial load necessary for the first contact of its outer surface with the rigid cylinder wall at first falls and then (after certain value of height) stabilizes.
It follows from Figure 5 that the axial load necessary for full contact of the outer surface of the sealing element with the wall of the casing also decreases with increasing the height, and then (after its certain value) stabilizes.
The distribution of contact pressure between the outer surface of the sealing element and the rigid cylinder wall depending on the coordinate z was depicted in Figure 6. As is seen from Figure 6 the greatest value of the contact pressure is achieved in the lower section of the sealing element. With increasing the value of z the contact pressure decreases and then after certain value of the height of the sealing element it disappears.
![]()
Figure 4. The graph of dependence of axial load necessary for the contact of the outer surface of the sealing element with the rigid cylinder wall on its height.
![]()
Figure 5. The graph of dependence of the axial load necessary for full contact of the outer surface of the sealer with the rigid cylinder wall on its height.
![]()
Figure 6. The graph of dependence of the character of contact pressure distribution depending on coordinate z.
![]()
Figure 7. The graph of dependence of the axial load Q necessary for precompressing the sealing element to the first contact of its outer surface with the rigid cylinder wall with regard to heredity.
![]()
Figure 8. The graph of dependence of the axial load P necessary for recompressing the sealing element to full contact of its outer surface with the rigid cylinder wall.
As is seen from Figure 7 and Figure 8, for constant value of axial deformation in the section of application of external force with regard to heredity the stress greatly relaxes. For 40 s. its value at the point of application of the external force decreases about 5 times, and then stabilizes. This may cause violation of tightness of the sealer.
The same picture is observed when deformation of the sealer happens uniformly. This time axial stress relaxation for different velocities of deformation occurs differently (Figure 9 and Figure 10).
7. Conclusions
In this article, we determine stress-strain state of the sealing element in the form of a hollow cylinder based on theoretical investigations. Influence of viscous-elastic properties of the material of the sealing element on its sealing ability is realized based on the hypothesis of elastic analogy.
1) The dependence between the magnitude of the axial load necessary for tightness and geometrical sizes under unilateral compression of the sealing element, is established. It is shown that, with decrease in the height of the sealing element the axial load necessary for achieving tightness, greatly increases. Furthermore, the limiting value of the height of the sealing element under unilateral compression, above of which contact pressure depends a little on the magnitude of the axial load, is defined.
2) The obtained expression allows to determine the character of contact pressure distribution between the surface of the sealer and the rigid cylinder wall depending on its physical-mechanical characteristics and geometrical sizes.
3) Based on linear laws of heredity the analytic formula allowing to determine the axial load necessary for tightness of the surface of the sealing element and cylinder wall depending on its physic-mechanical properties and geometrical sizes is found. The current work demonstrates that viscous elastic properties of the sealing material greatly influence on its sealing ability and their ignorance may lead to incorrect conclusions.
4) The results of numerical calculations are represented in the form of graphs of external force necessary for achieving sightless. It is shown that, viscous-elastic properties of sealer’s material greatly influence on its sealing ability. Because of heredity of the sealer’s material, the values of external forces in some cases drop about four times.