Improving Local Priority Hysteresis Switching Logic Convergence ()
1. Introduction
One of the earliest definitions of the term “adaption” was introduced by Drenick and Shahbender [2] in 1957:
“Adaptive systems in control theory are control systems that monitor their own performance and adjust their parameters in the direction of better performance.”
Adaptive control ensures the satisfactory performance of a closed-loop system by switching among a set of candidate controllers K when no single controller k can achieve the targeted performance objectives.
Two techniques have generally been used to achieve this goal: unfalsified adaptive control [3] [4] [5] and multiple model adaptive control [6] [7] [8]. In both cases, the switching process is supervised by a unit that provides the best controller k for the feedback loop from the controller set K based on the plant input/output data and performance criterion
. Figure 1 shows the general architecture of an adaptive control system.
One serious challenge associated with adaptive control switching systems is a type of instability called chattering. Chattering means the switching system will cycle among two or more candidate controllers without ever converging. Various techniques can help to avoid chattering for a finite and infinite candidate controller set. Using a continuum of candidate controllers instead of a finite set allows for greater flexibility for the adaptive control system to manage uncertainty [9] [10] [11] [12].
One technique involves the hysteresis switching algorithm reported by Morse and Middleton in [13] [14]. Morse and his co-workers demonstrated adaptive control convergence for a finite controller set. Also, Hespanha et al. [9] [10] and Stefanovic et al. [11] proved adaptive control convergence for an infinite controller set.
These studies contributed to ensuring adaptive control switching system convergence by adding constraints to the switching scheme that required strictly positive hysteresis and local priority constants.
Unfortunately, however, such constraints in the switching scheme can hinder the adaptive control system in achieving optimality.
This paper contributes to the body of knowledge by easing the local priority hysteresis switching logic constraints in switching schemes based on the persistent excitation assumption. Easing these constraints is necessary to achieve the objective of high performance.
This paper is organized as follows. In Section 2, preliminary facts are given. Section 3 reviews definitions of local priority hysteresis switching logic. Section 4 contains the main results. Simulation examples are shown in Section 5. The conclusion and avenues for future work are provided in Section 6.
2. Preliminaries
Definition 1. Suppose that
is twice differentiable on
and that for some
,
(1)
Then, f is uniformly convex on X.
With respect to uniform convexity, if
is uniformly convex on a connected set
, then for every
that satisfies (1), we have ( [15], Prop.A.23)
(2)
for any
satisfying (1).
Definition 2. A function
is said to be equi-quasi-positive definite (EQPD) in k if for some continuous monotonic function
with
and
, it holds for all sufficiently large values of
and t that
exists, and (3)
(4)
Definition 3. (Second order Taylor theorem expansion) Let
, and let
be twice continuously differentiable over C. Then,
or
for
where the gradient
of the function
is a row vector of size n, i.e.,
the Hessian
is an
matrix.
and
Lemma 1. (Weierstrass theorem [15] ) Let
be a non-empty subset of
and let
be a lower semicontinuous function at all points of
. If
is compact, then
exists.
Definition 4. The system is persistently excited if for all sufficiently large values of
and all p values it holds that
for some
.
Under the persistent excitation assumption and for a sufficient length of time t, the function
is a uniformly convex function in p. Therefore, if the system is persistently excited, the monitoring signal will become uniformly convex.
The definition of persistent excitation (PE) is critical in adaptive scheme studies that seek parameter convergence; see, for example, [16] - [21].
3. Local Priority Hysteresis Switching Logic
In this section, we present notations and definitions of local priority hysteresis switching logic. The intent is to introduce a switching scheme that can be applied when the unknown parameters of the system belong to a continuum set. Due to the differences between finite and infinite sets of candidate controllers, an infinite set of candidate controllers (typically, a continuum of controllers) can result in a better environment that facilitates the feasibility assumption (i.e., there is a controller in the candidate controller set can satisfy the adaptive control performance).
The supervisory control approach [22] [23] is used to achieve or maintain a desired performance level in a closed-loop system via switching through the given set of candidate controllers. The basic idea in selecting a controller strategy is to determine which nominal process model is associated with the smallest monitoring signals “
”. Then, the corresponding candidate controller can be selected.
Assume a linear single-input and single-output (SISO) finite-dimension uncertain process
shown in Figure 2.
is assumed to be a stabilizable and observable model with control input signals u and measured output signals y.
The supervisor contains three subsections, as shown in Figure 2.
1) Multi-estimator
—is a dynamic system with inputs of u and y and outputs of the signals
,
.
is a compact subset of a finite-dimension normalized linear vector space.
2) Monitoring signal generator
—is a dynamic system with inputs of estimation errors
and outputs of monitoring signals
,
where
is defined as the integral norms of the estimation errors, called monitoring signals.
3) Switching logic
—involves a switched system with inputs of the monitoring signals
and outputs of the parameters that optimize the performance criterion
, which is defined as follows.
(5)
takes its values in
and is used to select the associated controller parameter.
![]()
Figure 2. Supervisory control block diagram.
Each
converges to y if the transfer function of
equals the nominal process model transfer function
in the absence of disturbances. Unmodeled dynamics and noise, which represent disturbance inputs and noise signals, are represented by d and n, respectively.
Assume that the transfer function of
from u, the output of the multi-controller “
”, and y belong to a family of admissible process model transfer functions.
(6)
For each p,
denotes a family of transfer functions centered in a known nominal process model transfer function
, where p is a parameter with values based on a given index set
and
is typically a continuum. In the absence of noise, the unmodeled dynamics and disturbances (6) can be written as follows.
(7)
The state-space equations for the three subsystems are described in [10] ; the multi-estimator
can be stated as follows.
,
where
is the estimated state that is assumed to be available for the controller at all times and
is a stable matrix.
The matrix
is designed based on each
so that
exists and is unique (see reference [22] ; Section IV). Moreover, for
to form a continuum,
is assumed to be linearly dependent on p, which ensures tractability (see reference [22] ; Section XI). Therefore, the matrix
can be written as follows.
(8)
For a SISO system, A is a nonzero matrix with a dimension
, p is
unknown process parameters, and b is a
vector.
In [9], the candidate controller set =
is selected so that each
,
is a controller stabilizing all the process models in
, where
is any element of
. We assume that feasibility holds. A set
is defined as follows.
(9)
where
is a norm function in
and
is a proper positive constant. The output of
at each instance is
. In this case, a hysteresis constant
is selected, and
. Assume that at time
,
switches to
and remains fixed until time
, such that the following inequality is satisfied.
We set
. Repeating these steps yields a sequence of switching signals that converge as time passes.
Assume
is the controller parameter associated with the process parameter
, then the active controller in the feedback loop
changes as follows.
(10)
A key result is the local priority hysteresis switching convergence lemma, which can be stated as follows.
Lemma 2. (Convergence Lemma [10] ) Assume that both of the following hold:
1) Monotonicity: For all p it holds that
for all
2) Feasibility: A
exists for which the monitoring signal is uniformly bounded
Then, if constant
and hysteresis constant h are strictly positive, the local priority hysteresis switching logic converges after a finite number of switches.
A concern with constant
required by Lemma 2 is that the constant
prevents the adaptive system from switching to a new parameter
that minimizes the monitoring signal
if this parameter is in the set
(i.e.,
). Another notable issue with this lemma is that the strictly positive hysteresis constant h can slow the supervisor’s adaptive response and limit the accuracy with which the supervisor can minimize the monitoring signal
to
.
In the following section, we re-examine the local priority hysteresis switching logic convergence when the constraints on the switching scheme are eased, allowing the supervisor to instantaneously respond and continuously use the optimal, adaptive, zero-hysteresis trend.
(11)
4. Main Results
The following lemmas and theorem establish that under the PE assumption, if the strictly positive local priority and hysteresis constants are eased in the local priority hysteresis switching logic convergence lemma, the optimal process parameter
, as defined in (5), still converges as
under the same conditions (i.e., monotonic monitoring signal and feasible system) given in [9] and with the identical monitoring signal.
Recall that the authors in [9] use the following monitoring signal.
(12)
Since
,
and
,
can be written as follows.
(13)
Then,
(14)
The following lemmas will be used in the proof of the main result.
Lemma 3. Let
be monotonically increasing in t for all p, and suppose that a minimizing value
exists for all t. Then,
for all
.
Proof. By monotonicity
(15)
Also, since
minimizes
(16)
From (15) and from (16)
Hence,
☐
Lemma 4. Let
be monotonically increasing in t for all p, and suppose that a
minimizing value
exists for all t. If the system is persistently
excited (def. 4), then
.
Proof. Writing the monitoring signal
in the second order Taylor theorem expansion form
(17)
where
can be written as
and
.
Since
minimizes , we have
, we have
 (18)
(18)
Additionally, since the system is persistently excited,
 (19)
(19)
From (18) and (19), Equation (17) can be written as follows.
 (20)
(20)
or, equivalently,
 (21)
(21)
By monotonicity
 (22)
(22)
Therefore,
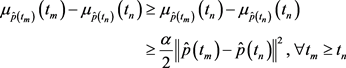
and hence for all 

☐
Theorem 1. (Main Result) Consider the supervisory control system in Figure 2.
Assume that the following conditions hold.
1) Monotonicity: For all p, it holds that
 for all
for all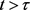 .
.
2) Feasibility: A  value exists for which the monitoring signal is uniformly bounded, as follows.
value exists for which the monitoring signal is uniformly bounded, as follows.

If the system is persistently excited (def. 4), then the optimal process parameter  converges as t increases to infinity to a point in the closure of the set
converges as t increases to infinity to a point in the closure of the set .
.
Proof. By feasibility and by Lemma 3,  exists and
exists and ![]() is monotonic in t and has an upper bound. Hence,
is monotonic in t and has an upper bound. Hence,
![]() (23)
(23)
![]() (24)
(24)
Since the systems is persistently excited, it follows from Lemma 4 that for all![]() ,
,
![]() (25)
(25)
Thus, for all![]() , it holds that
, it holds that
![]()
Therefore, for every![]() , there exists
, there exists ![]() such that for all
such that for all![]() .
.
![]()
Moreover, ![]() as
as![]() . Since,
. Since, ![]() ,
, ![]() is a nondecreasing continuous function that satisfies
is a nondecreasing continuous function that satisfies ![]() and
and ![]() for
for
![]() , it follows that for every
, it follows that for every![]() , a
, a ![]() exists, such that
exists, such that ![]() for all
for all![]() . Therefore, the sequence
. Therefore, the sequence ![]() is a Cauchy sequence. Since every Cauchy sequence converges [24], it follows that
is a Cauchy sequence. Since every Cauchy sequence converges [24], it follows that ![]() converges as
converges as ![]() to a point in the closure of the set
to a point in the closure of the set![]() .
.
Remark 1. (Performance Improvement) According to the certainty equivalence concept [25],
“The nominal process model with the smallest performance criterion signal ‘best’ approximates the actual process, and therefore the candidate controller associated with that model can be expected to do the best job of controlling the process.”
The basic idea is to determine which nominal process model is associated with the smallest monitoring signals. Then, the corresponding candidate controller can be selected.
As shown in theorem 1, the approach introduced in this paper (which relies on easing the local priority hysteresis switching logic constraints) improves adaptive controller convergence. Based on certainty equivalence [25], this method also improves adaptive control performance.
5. Simulation Examples
In this section, two systems are examined to demonstrate the unconstrained performance criterion introduced in this work and how it can converge to an optimum solution within a certain time without unstructured uncertainty or plant/sensor noise. In both examples, the reference signal is set to a unit step function.
Example 1: Consider the model reference adaptive control in Figure 2 with a
first-order model reference ![]() and actual plant
and actual plant![]() , where p is
, where p is
a parameter with values from index set ![]() and
and ![]() is
is![]() . The simulation starts with the initial process parameter set to
. The simulation starts with the initial process parameter set to![]() . The monitoring signal “
. The monitoring signal “![]() ” converges to the optimum value if parameter p converges to −4. The results are shown in Figure 3 and Figure 4. The graph in Figure 3 shows that the
” converges to the optimum value if parameter p converges to −4. The results are shown in Figure 3 and Figure 4. The graph in Figure 3 shows that the
![]()
Figure 3. Simulation results for example 1.
![]()
Figure 4. Simulation results for example 1.
performance criterion instantaneously and continuously responds and the output of the plant converges to the output of the reference model “![]() ” when “
” when “![]() ”, which is the point when the error “e” reaches zero. The graph in Figure 4 shows the rapid and smooth convergence of the error and process parameters to optimal values. In both graphs, exact matching is achieved.
”, which is the point when the error “e” reaches zero. The graph in Figure 4 shows the rapid and smooth convergence of the error and process parameters to optimal values. In both graphs, exact matching is achieved.
Example 2: In this example, a second-order system shows how the unconstrained performance criterion manages a system that exhibits a transient response. Consider the model reference adaptive control in Figure 2 with a second-order
model reference ![]() and actual plant
and actual plant![]() ,
,
where ![]() is a parameter with values from the index set
is a parameter with values from the index set ![]() and
and ![]() is
is![]() . The simulation starts with the initial process parameter set to
. The simulation starts with the initial process parameter set to![]() . The results are shown in Figure 5 and Figure 6. The graph in Figure 5 shows that the error “e” reaches zero when the process parameter “
. The results are shown in Figure 5 and Figure 6. The graph in Figure 5 shows that the error “e” reaches zero when the process parameter “![]() ” converges to −6. The graph in Figure 6 shows the smooth convergence of the error and process parameter to the optimal values over a short time. In this example, the plant performance and error convergence results are satisfactory, and exact matching is achieved.
” converges to −6. The graph in Figure 6 shows the smooth convergence of the error and process parameter to the optimal values over a short time. In this example, the plant performance and error convergence results are satisfactory, and exact matching is achieved.
6. Conclusion and Future Work
6.1. Conclusion
In this paper, we examined the local priority hysteresis switching logic and established performance criteria under which the hysteresis constant can be set to zero. The main results indicate that when the convergence lemma conditions
![]()
Figure 5. Simulation results for example 2.
![]()
Figure 6. Simulation results for example 2.
(i.e., monotonic monitoring signal and feasible system) hold, the PE assumption ensures convergence in local priority hysteresis switching logic without adding constraints to the switching logic. Easing these constraints improves adaptive control convergence, which results in improved performance.
6.2. Future Work
The quadratic model reference performance criterion in the example satisfies the EQPD condition, but it lacks the fading memory term, which may lead to difficulties for plants with unstructured uncertainty or plant/sensor noise. In those cases, a performance criterion with a fading memory term that satisfies the EQPD condition must be designed. Whether such a performance criterion exists remains an open question to address in future studies.