1. Introduction
The basic elements of the multiplicative number theory are the prime numbers (positive integers divisible only by 1 and themselves). There is a mixture of randomness and hidden regularity in their behavior ([2 - 4]). The oldest conjecture in number theory is considered to be that of Christian Goldbach. As shown in [5], in his letter to Leonhard Euler, dated 7 June 1742, Christian Golbach mentioned that every integer greater than 5 can be written as the sum of three primes. Euler replied in a letter dated 30 June 1742 reminding Go7ldbach of an earlier conversation they had in which Goldbach remarked that his original conjecture was that every even integer greater than 2 can be written as the sum of two primes. In this letter, Euler stated: “That … every even integer is the sum of two primes, I regard as a completely certain theorem, although I cannot prove it.” As Goldbach considered 1 to be a prime, today his conjecture is known as stating that: “Every even integer larger than 4 is the sum of two primes.” Goldbach’s Conjecture has been verified for larger and larger even integer but still remained unproven.
If Goldbach’s Conjecture is true then to every even positive integer
there correspond two primes p and q such that:
. Assuming
, this implies that:
,
showing that either:
, or, if
, that
is located at the middle of the distance between the two primes.
Conversely, if n is a prime then
and Goldbach’s Conjecture is true. If n is a positive composite integer strictly larger than 3, located at the middle of the distance between two primes
, then:
,
implying that:
.
Therefore, if n is a prime, or a positive composite integer
, and every such an integer is located at the middle distance between two primes, then 2n is the sum of two primes and Goldbach’s Conjecture is true for every
, and therefore, for every
.
In [1] there is the proof that every positive composite integer n, strictly larger than 3, is located at the middle of the distance between two primes and, implicitly, that Goldbach’s Conjecture is true for 2n as well. The present paper is a follow up of paper [1], bringing additional and complementary details of the proof of Goldbach’s Conjecture, insisting on the existence and the number of Goldbach’s representations of the positive even integers as sums of pairs of primes.
2. The frames of symmetric odd positive integers
Assume that n is an odd composite positive integer strictly larger than 3.
Frame I for n odd composite positive integer:

The odd integers from the interval
, symmetric with respect to n, are put in two Groups, as shown in Frame I. Each column contains two odd integers, symmetric with respect to n, called matching integers, whose sum is equal to 2n. Except n, which is the center of symmetry, the even numbers from the interval
are not included in Frame I. Also, the odd integer
is also missing from Frame I because it matches the integer 1 which is not relevant in this context. The smallest integer from Group 1 is matched with the largest integer from Group 2 but the difference between the matching integers gradually decreases by a constant rate equal to 4.
In each Group of Frame I, there are primes or odd composite positive integers. Let us notice that if
is a prime factor of n and an integer
from any Group is a multiple of
, then its matching integer
is also a multiple of
because:
As a consequence, if an odd integer
from a Group is relative prime with n then its matching integer
is also relative prime with n. An odd prime which is not a factor of n can match with an odd prime or with an odd composite integer relative prime with n but not with an odd composite positive integer divisible by an odd prime factor of n. An odd composite integer can match with a prime or with another odd composite integer but the two odd composite integers must be either relative prime with n or divisible by the same od prime factor of n.
In Frame I, the number of odd integers from Group 1 is:
,
and in Group 2 the number is the same:
,
where
is the integer part of the real number x.
The number of primes in Group 1 is:
, where
is the number of primes not exceeding the real number x. The number of primes in Group 2 is:
.
As n is an odd composite integer, let:
be the prime factorization of n, where
are odd primes.
The primes relative prime with n from Frame I are grouped into three disjoint Classes:
Class 1 is the set of primes relative prime with n belonging to the interval
.
Class 2 is the set of primes relative prime with n from Frame I belonging to the interval
.
Class 3 is the set of primes relative prime with n from Frame I belonging to the interval
.
The primes from Class 1 have odd composite multiples in both Groups. The primes from Class 2 have odd composite multiples only in Group 2. The primes from Class 3 have no odd composite multiples in the corresponding Frame I. Let us mention that if the square of the smallest prime from Class 2 exceeds
then all the odd composite multiples relative prime with n are generated by primes relative prime with respect to n from Class 1.
Assume that n is an even composite positive integer strictly larger than 3. Its Frame is:
Frame II for n even composite positive integer:

All the comments made about Frame I remain valid for Frame II as well. Briefly, in Frame II, the number of odd integers from Group 1 is:
,
and in Group 2 the number of odd integers is the same:
.
The number of primes in Group 1 is:
, where −1 is needed because the prime 2 does not belong to Group 1 and cannot be counted. The number of primes in Group 2 is:
.
As n is an even composite integer,
,
is the prime factorization of n, where
are odd primes.
The primes relative prime with n from Frame II are grouped in three disjoint Classes:
Class 1 is the set of primes relative prime with n from Frame II belonging to the interval
.
Class 2 is the set of primes relative prime with n from Frame II belonging to the interval
.
Class 3 is the set of primes relative prime with n from Frame II belonging to the interval
.
The primes from Class 1 have odd composite multiples in both Groups. The primes from Class 2 have odd composite multiples only in Group 2. The primes from Class 3 have no odd composite multiples in the corresponding Frame II. Let us mention that if the square of the smallest prime from Class 2 exceeds
then all the odd composite multiples relative prime with n are generated by primes relative prime with respect to n from Class 1.
When n is given, its corresponding Fram contains the prime factors of n, the primes relative prime with n, the odd composite multiples of the prime factors of n, and the odd composite multiples of the primes that are relative prime with n. Obviously, all prime factors of n are located in Group 1. Denote by a the number of prime factors and their odd composite multiples from Group 1. Let b be the number of odd composite multiples of the prime factors of n from Group 2. Let
be an odd integer from Group 1 and
be an odd integer from Group 2. They match if they are symmetric with respect to n, which means:
.
This equality shows that if
is a prime factor of n then
has to be an odd composite multiple of this prime factor. If
is an odd composite multiple of a prime factor of n then
is an odd composite multiple of the same prime factor of n. On the other hand, if
is a prime relative prime with n then
may be only a different prime relative prime with n or an odd composite multiple relative prime with n of a different prime relative prime with n. If
is an odd composite multiple relative prime with n then
may be either a prime relative prime with n and relative prime with
or an odd composite multiple relative prime with n of a prime relative prime with n and relative prime with
. This elementary analysis shows that the prime factors of n and their odd composite multiples match together and that
.
Remark: If
there are no odd prime factors of n and there are some differences. As there are no odd prime factors of n, we have
. If
is an integer from Group 1 and 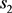 a matching integer from Goup 2, we have:
a matching integer from Goup 2, we have:
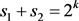 .
.
If 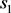 is a prime, then
is a prime, then  cannot be a multiple of
cannot be a multiple of 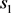 because this would make
because this would make 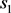 to be a prine factor of
to be a prine factor of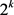 , which is absurd. Similarly, if
, which is absurd. Similarly, if  is a prime, then
is a prime, then 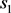 cannot be a multiple of
cannot be a multiple of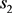 . Also,
. Also, 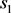 and
and 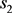 must be relative prime because if they have a common prime factor p, it would be a factor of
must be relative prime because if they have a common prime factor p, it would be a factor of 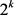 as well, which is absurd.
as well, which is absurd.
Except the prime factors of n and their odd composite multiples, Group 1 contains  odd integers representing
odd integers representing  primes relative prime with n from Class 1,
primes relative prime with n from Class 1, ![]() primes relative prime with n from Class 2,
primes relative prime with n from Class 2, ![]() primes relative prime with n from Class 3, and
primes relative prime with n from Class 3, and ![]() distinct odd composite multiples relative prime with n of primes relative prime with n from Class 1. The number of primes relative prime with n in Group 1 is:
distinct odd composite multiples relative prime with n of primes relative prime with n from Class 1. The number of primes relative prime with n in Group 1 is:
![]() .
.
Except the odd composite multiples of prime factors of n, Group 2 contains ![]() odd integers representing
odd integers representing ![]() primes relative prime with n from Class 3 and
primes relative prime with n from Class 3 and ![]() distinct odd composite multiples relative prime with n of primes relative prime with n from Class 1 and Class 2. The number of primes relative prime with n in Group 2 is:
distinct odd composite multiples relative prime with n of primes relative prime with n from Class 1 and Class 2. The number of primes relative prime with n in Group 2 is:
![]() .
.
The rate of generating odd composite multiples relative prime with n of primes relative prime with n is lower than the rate of generating odd integer spaces between odd composite multiples to accommodate other primes relative prime with n. If, for instance, p is a prime relative prime with n, from Class 1, it generates its odd composite multiples at a rate of ![]() and leaves extra spaces in between its multiples for other primes at a rate of
and leaves extra spaces in between its multiples for other primes at a rate of![]() . From this number of odd composite multiples of p we have to discount those odd multiples of p that are not relative prime with n. If we have two primes p and q, relative prime with n, from Class 1, then if p and q have a common odd composite multiple relative prime with n it has to be taken only once because we count the distinct odd composite multiples relative prime with n generated by the primes from Class 1 in Group 1 and by the pries from Class 1 and Class 2 in Group 2. Therefore, the rate of generating odd composite multiples relative prime with n by primes relative prime with n is slower than the rate of generating interspaces to accommodate other primes relative prime with n in Group 1 and Group 2. In general, the process of generating odd composite multiples becomes slower when we discount the odd composite multiples divisible by prime factors of n and count only distinct odd composite multiples of primes relative prime with n from Class 1 in Group 1 and from Class 1 and Class 2 in Group 2. As the rate of generating distinct odd composite multiples relative prime with n by primes relative prime with n from Class 1 in Group 1 and from Class 1 and Class 2 in Group 2 is smaller than the rate of generating other primes in between the odd composite multiples generated by the primes from Class 1 and, eventually, from Class 2, we have:
. From this number of odd composite multiples of p we have to discount those odd multiples of p that are not relative prime with n. If we have two primes p and q, relative prime with n, from Class 1, then if p and q have a common odd composite multiple relative prime with n it has to be taken only once because we count the distinct odd composite multiples relative prime with n generated by the primes from Class 1 in Group 1 and by the pries from Class 1 and Class 2 in Group 2. Therefore, the rate of generating odd composite multiples relative prime with n by primes relative prime with n is slower than the rate of generating interspaces to accommodate other primes relative prime with n in Group 1 and Group 2. In general, the process of generating odd composite multiples becomes slower when we discount the odd composite multiples divisible by prime factors of n and count only distinct odd composite multiples of primes relative prime with n from Class 1 in Group 1 and from Class 1 and Class 2 in Group 2. As the rate of generating distinct odd composite multiples relative prime with n by primes relative prime with n from Class 1 in Group 1 and from Class 1 and Class 2 in Group 2 is smaller than the rate of generating other primes in between the odd composite multiples generated by the primes from Class 1 and, eventually, from Class 2, we have:
![]() (1)
(1)
Finally, let m be the number of matching odd composite multiples relative prime with n of primes relative prime with n.
3. the proof of goldbach’s conjecture
As the proof of Goldbach’s Conjecture is the same for each of the two Frames, let us simplify and unify the notations. In this section: N is the number of odd integers from Group 1 or Group 2; ![]() is the number of primes from Group 1 that are not prime factors of n;
is the number of primes from Group 1 that are not prime factors of n; ![]() is the number of primes from Group 2;
is the number of primes from Group 2; ![]() is the number of distinct odd composite multiples in Group 1 of the prime numbers from Class 1;
is the number of distinct odd composite multiples in Group 1 of the prime numbers from Class 1; ![]() is the number of distinct odd composite multiples in Group 2 of the primes from Class 1 and Class 2; m is the number of matching pairs of odd composite multiples relative prime with n from Group 1 and Group 2; a is the number of multiples of prime factors of n in Group 1; b is the number of multiples of prime factors of n in Group 2. We have:
is the number of distinct odd composite multiples in Group 2 of the primes from Class 1 and Class 2; m is the number of matching pairs of odd composite multiples relative prime with n from Group 1 and Group 2; a is the number of multiples of prime factors of n in Group 1; b is the number of multiples of prime factors of n in Group 2. We have:
![]() .
.
As![]() , we get:
, we get:
![]() ,
,
and, adding m to both sides, we have:
![]()
or, equivalently,
![]() . (2)
. (2)
But ![]() is the number of odd composite multiples relative prime with n from Group 1 that match primes from Group 2 and
is the number of odd composite multiples relative prime with n from Group 1 that match primes from Group 2 and ![]() is the number of odd composite multiples relative prime with n from Group 2 that match primes from Group 1. Then, there are matching primes from Group 1 and Group 2, and, therefore, Goldbach’s Conjecture is true, if and only if:
is the number of odd composite multiples relative prime with n from Group 2 that match primes from Group 1. Then, there are matching primes from Group 1 and Group 2, and, therefore, Goldbach’s Conjecture is true, if and only if:
![]() , and
, and![]() , (3)
, (3)
which is true because:
a) If:
![]() ,
,
then there are not enough primes in Group 1 to match the odd composite multiples relative prime with n from Group 2 that are supposed to match primes from Group 1.
b) If:
![]() ,
,
then there are not enough primes in Group 2 to match the odd composite multiples relative prime with n from Group 1 that are supposed to match primes from Group 2.
c) If:
![]() ,
,
then we have:
![]()
which contradicts the inequality (1).
Therefore, the inequalities (3) are true, proving that Goldbach’s Conjecture is true, and the number (2) gives the number of Goldbach solutions for 2n.
4. numerical examples
From computational point of view, it is quite easy to deal with prime numbers. In Wolfram’s software Mathematica ([6]), for instance, there are two useful functions: Prime[n], giving the n-th prime number, and PrimePi [x], giving the number of primes not exceeding the real number x, known in number theory as the function![]() . Goldbach solutions for the even integer 2n may be obtained online, by typing on GOOGLE: “Goldbach Conjecture Calculator - Tester - Online Tool - dCode.” Typing “Prime Counting Function Calculator - Online Software Tool”, we can choose: “Prime Counter
. Goldbach solutions for the even integer 2n may be obtained online, by typing on GOOGLE: “Goldbach Conjecture Calculator - Tester - Online Tool - dCode.” Typing “Prime Counting Function Calculator - Online Software Tool”, we can choose: “Prime Counter ![]() Calculator”, or “Prime Factors Decomposition”, or “Multiples of a Number”, or “Divisors of a Number.”
Calculator”, or “Prime Factors Decomposition”, or “Multiples of a Number”, or “Divisors of a Number.”
Example 1. Let ![]() The corresponding Frame II is:
The corresponding Frame II is:
![]()
![]()
The bold numbers represent primes. Tne numbers followed by the asterisk * are odd multiples of the prime factors of n. The other integers are odd multiples of the primes relative prime with n.
We have:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,![]() .
.
![]() .
.
The number of matching primes, or the number of Goldbach solutions for 100, is:
![]()
or, equivalently,
![]() .
.
Indeed, they are: (3, 97), (11, 89), (17, 83), (29, 71), (41, 59), (47, 53).
Let us notice that in the two pairs of matching odd composite multiples, namely,
![]()
the components are relative prime multiples of primes from Class 1.
Example 2: In the previous example, the Frame was given and examined afterwards. It is possible, however, to reverse this approach and to show that the primes from Class 1 generate the entire corresponding Frame. Let![]() . The corresponding Frame I, containing the pairs of odd positive integers symmetric with respect to 33, has Group 1 containing the odd positive integers from 3 to 31, going forward, and Group 2 containing the odd positive integers from 35 to 63, going backwards. Thus:
. The corresponding Frame I, containing the pairs of odd positive integers symmetric with respect to 33, has Group 1 containing the odd positive integers from 3 to 31, going forward, and Group 2 containing the odd positive integers from 35 to 63, going backwards. Thus:
1)![]() .
.
2) The odd prime factors of n are 3 and 11.
3) The odd multiples of the prime factors in Group 1 are: 3, 9, 11, 15, 21, 27.
4) The odd multiples of the prime factors in Group 2 are: 39, 45, 51, 55, 57, 63.
5) Class 1 consists of the primes from the interval![]() , relative prime with n, namely: {5, 7}.
, relative prime with n, namely: {5, 7}.
6) There is only one odd composite multiple of the primes from Class 1 relative prime with n in Group 1, namely: 25.
7) All odd positive integers from Group 1 not mentioned at steps 2, 3, 5, and 6 are prime numbers, namely: 13, 17, 19, 23, 29.
8) As the smallest prime, relative prime with respect to n, larger than the primes from Class 1, namely 13, has the square larger than![]() , this means that in Group 2, except the integers listed at step 4, we have only prime numbers and odd composite multiples of the primes from Class 1.
, this means that in Group 2, except the integers listed at step 4, we have only prime numbers and odd composite multiples of the primes from Class 1.
9) The odd composite multiples of the prime numbers from Class 1 in Group 2 are: 35, 49.
10) All the integers from Group 2 not mentioned at steps 4 and 9 are prime numbers, namely: 37, 41, 43, 47, 53, 59, 61.
11) Summarizing, the Frame of the number ![]() is shown below:
is shown below:
![]()
Example 3: In the Frame corresponding to ![]() given in the previous example, we have:
given in the previous example, we have:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Let illustrate in this example why the inequality:
![]() ,
,
holds. We notice that:
The prime factor 3 has 4 odd composite multiples in Group 1, namely 9, 15, 21, 27, and 5 odd composite multiples in Group 2, namely 39, 45, 51, 57, 63.
The prime factor 11 has 0 odd composite multiples in Group 1, and 1 odd composite multiple, 55, in Group 2.
Thus, the prime factors 3 and 11 have a total of 4 odd composite multiples in Group 1 and 6 odd composite multiples in Group 2. Counting the prime factors 3 and 11 themselves among the odd multiples, we get that the number of odd multiples of the prime factors in Group 1 is ![]() and the number of odd multiples of the prime factors in Group 2 is
and the number of odd multiples of the prime factors in Group 2 is![]() .
.
Class 1 is the set of primes relative prime with n from the interval![]() , namely {5, 7}.
, namely {5, 7}.
The prime 5 from Class 1 has 2 odd composite multiples in Group 1, namely 15 and 25, and 3 odd composite multiples in Group 2, namely 35, 45, and 55.
The prime 7 from Class 1 has 1 odd composite multiple, namely 21, in Group 1, and 3 odd composite multiples in Group 2, namely 35, 49, 63.
As we are interested only in the odd composite multiples that are relative prime with n, we notice that:
The prime 5 from Class 1 has 1 odd composite multiple relative prime with n, namely 25, in Group 1, and 2 odd composite multiples relative prime with n, namely 35 and 55, in Group 2.
The prime 7 from Class 1 has no odd composite multiples relative prime with n in Group 1 and 2 odd composite multiples relative prime with n in Group 1, namely 35, 49.
As 35 is a common odd composite multiple relative prime with n of both 5 and 7, it has to be counted only once.
Therefore, the primes 5 and 7 from Class 1 generate the following distinct odd composite multiples relative prime with n: 25 in Group 1 and 35, 49 in Group 2. Thus, ![]() ,
, ![]() , and we have:
, and we have:
![]() ,
,
confirming the inequality (1).
5. conclusion
Goldbach’s Conjecture is the oldest conjecture in number theory. It states that every even integer strictly greater than 4 is the sum of two primes. There have been many empirical verifications of it, up to astronomic numbers, but it has remained unproven since 1742. The paper [1] formulated an equivalent property about a hidden symmetry of primes stating that for every positive composite number n, strictly larger than 3, there are two primes symmetric with respect to n. The paper [1] contained a proof of this prime symmetry property and, implicitly, of Goldbach’s conjecture for 2n as well. The present paper is a follow up of paper [1] bringing explicit new and complementary details about the proof given in [1], insisting on the existence and the number of Goldbach representations of even positive integers as sums of pairs of primes.
Acknowledgements
The author thanks Yavonne Zhang, Editorial Assistant of Natural Science, for her very valuable advice and professional recommendations.