Fast Fourier Transform Based Computation of American Options under Economic Recession Induced Volatility Uncertainty ()
1. Introduction
Financial mathematics encompasses many relevant areas in which option valuation is one of them and connects many different fields of study in mathematics. It relies on the application of various mathematical concepts and tools for survival. Such concepts are Probability theory, optimization theory, numerical analysis, partial differential equations, Ordinary Differential Equations, integral representations, transformation and many more. Among various transformation techniques obtainable in Mathematics such as Hankel transform, Mellin transform, Hilbert transform, Laplace transform, z-transform, and Fourier transform, this paper applies fast Fourier transform based computation of Options focusing on uncertainty in the options value induced by Economic Recession.
Instability of Economy has created a wide disparity between Economic activities and the values of Assets found in the economy. It is very obvious that Assets’ values are been affected by the state of the Economy. The effect of Economic recession to the falling of the payoff of investments and standard of living is enormous and should not be taken for granted. This is evident as the data from Nigeria Stock Exchange (NSE) indices prior to recession outbreak, during recession and after recession revealed huge lower performance of Nigeria stocks during the Nigeria economy recession of 2016. The National Bureau of Economic Research (NBER) has been recognised in the United States as an official body saddled with the responsibility of providing an accurate information on economic recession dates and business cycle publishing since 1929. The definition of recession according to NBER cited in [1] is a significant decline in economic activity spread across the economy, lasting more than a few months, normally visible in production, employment, real income, and other indicators. Some other definitions of economic recession obtainable in financial press emphasised that recession begins with two consecutive quarters of decline in Gross Domestic Product (GDP). NBER ponders on GDP as the single best measure of total economic activity and reflects on the GDP definition to be too narrow in measuring economic activity and to reliably date economic recessions. There exists scenario whereby recession may not include two consecutive quarters of negative growth such as United States recession of 2001 but according to Thomas Hsu [1] , declines in GDP are closely correlated to recession periods. Nigerian economic recession outbreak in year 2016 was based on decline in GDP and rise in some other macroeconomic indicators such as high inflation rate and unemployment rate after two consecutive quarters. Some measures were invented by axiomatic methods: for example, as cited in [2] . Probability Measure was invented by A.N. Kolmogoroff in 1933, Possibility Measure by L.A. Zadeh in 1978 and Uncertain Measure (B. Liu) in 2007 (see [2] [3] [4] [5] [6] ). Probability theory has been seen as the vehicle for dealing with uncertainty in finance and insurance risks. Probability theory as a mathematical theory is useful in describing and analysing situations where randomness or uncertainty are present [7] . Definition of uncertainty had been given by different authors in various scenarios. According to [8] (Dungan et al., 2002), Uncertainty is a multi-faceted characterization about data or predictions made from data that may include several concepts including error, accuracy, validity, quality, noise and confidence and reliability. Uncertainty connotes difficulty in predicting the outcome of an event due to inexact knowledge of information concerning the outcome of the event in a particular time. Uncertainty appears to endogenously increase during recessions, as lower economic growth induces greater micro and macro uncertainty [9] . It was stressed in [10] that investment growth experiences downward trend during the period of recession.
The following authors [11] - [21] have considered uncertainty with respect to models. The aspect of uncertainty in terms of economic recession was not discussed in their formulations. It was recognized that prices of insurance and financial risks are not solely determined by mathematics or economic theories but are also impacted by activities taking place in financial markets. During the period of economic crisis, prices of assets tend to change stochastically in the financial market (especially while dealing with stocks) since there is much tendency for fluctuations of asset prices due to fluctuation in the underlying term structures typically, the volatility variation. The study of volatility of stock prices is very essential due to its effect on the prices of stocks in the financial market. Pfante, O. and Bertschinger, N. (2018), [21] consider the uncertainty of volatility estimates from Heston Greeks. It was stressed in [22] that volatility has been the cause for several Statistical properties of observed stock prices processes. It was further emphasized in [22] that volatility clustering is commonly accompanied by other large fluctuations and similar for small changes. As volatility is not observed it has to be estimated from market prices, i.e., as the implied volatility from option prices. There is strong tendency that predictions of the volatility of asset prices induced by economic recession factor among other market risk factors may not really be accurate. This becomes a challenge for investors that do not like taking risk, that is, the risk averters. There are some existing methods of calculating the volatility of asset prices in financial market especially while dealing with instantaneous prices (i.e. the real time prices) of assets in the financial market. Among the methods known to us are 1) Standard deviation approach, 2) using Historical value of the volatility and 3) implied volatility. The Standard deviation approach tells us how tightly the stock price is grouped around the mean or moving average. When the prices are spread apart, the implication is that one has a relatively large standard deviation but if the prices are relatively closed to each other or bunched together, this connotes that the standard deviation is negligible.
The causal effect of volatility on stock prices is discussed briefly as follows. The stock market prices rise when volatility decreases and increase in volatility causes fall in stock market value (prices). Increase in volatility leads to increase in market risk but decrease in returns of the market. In the case of options on stocks market, the causal effect of volatility changes on options depends on the type. For example, increase in volatility leads to increase in call options value but for put options, increase in volatility leads to decline in the payoff of the put options vice versa. An intuition behind the introduction of recession induced volatility uncertainty is revealed by huge volatility fluctuations during the period of Economic recession compared to the period of normalcy (recession-free). This in turn affects investors’ prediction in the market. Since Economic recession induces a high level of uncertainty on investors activities to include decision making and the payoffs of stocks in general, we then proposes giving a close attention to volatility changes in relation to economic recession and financial models for options valuation. Nigeria economic recession outbreak in 2016 and its effects on the payoffs uncertainty of Nigeria Stocks Exchange (NSE) among other investments is among the motivating factors for proposing economic recession induced volatility formulation in Options pricing. A good knowledge of the behavior or the level of uncertainty in economic recession induced volatility by investor’s will help in decision making during recession period.
The rest part of the paper is organized as follows: Preliminaries on financial modeling is discussed in Section 2 in addition to some other subsections to include Fourier transform, uncertainty and uncertain measure. Section 3 deals with accounting for jumps in the asset price linked with recession, Section 4 shows the model formulation. Numerical Fourier based transform of options is presented in Section 5 while Section 6 is conclusion.
2. Preliminaries on Financial Modeling
2.1. Some Literature Review on Uncertainty
The theory of uncertainty in financial market could be traced back to the research work of [2] [3] [4] . Without uncertainty, the probabilities of risky events are known and frictionless markets can precisely price contracts contingent on risky events broadly. The volatility of the stock market or GDP is often used as a measure of uncertainty because when a data series becomes more volatile it is harder to forecast. Other common measures of uncertainty include forecaster disagreement, mentions of “uncertainty” in news, and the dispersion of productivity shocks to firms [9] . It was further stressed by Nicholas Bloom [9] that the volatility of stock markets, bond markets, exchange rates, and GDP growth all rise suddenly during economy recessions. In Philip et al. [10] , it was stressed that investment under the exposure of economic recession tends to have negative growth. This in turn poses a lot of challenges on investors in a financial or money market as investors’ decision in the market also depends on the daily information on the state of the economy.
In the history of options pricing in financial market, the famous Black - Scholes model [23] with the assumption of constant rate of return and volatility have been criticized by many researchers due to the fact that it does not reflect the stochastic nature of financial markets wholly. As a result of this deficiency in the B-S model, some other realistic models have been formulated and come to stay in the sense that the models shows better random movement of financial market. Example of such models are: Double exponential jump model, Regime switching model, Stochastic volatility models of Heston [24] , etc. In [25] , it was asserted that regime-switching behaviour captures changing preferences and beliefs of investors concerning asset prices as the state of financial market changes. Regime-Switching formulation in valuation of financial market was known to be introduced by J. Hamilton [26] . Since then, there have been some development on considering his suggestion. A closed form formula for the valuation of European call option in a two-state economy under the assumption of no-arbitrage was presented in [27] by Guo, X. European and American-style derivatives pricing was presented in [28] by Bollen using lattice-based approach.
Fourier transform approach of pricing options especially European-style options have been looked into by various authors. The one with great popularity known to us among others was that of Carr and Madan (1999) [29] in pricing European call option. Some other authors have also shown other mathematical formulation of Fourier transform of European options such as in [30] . As far as we know, the issue of economy recession factor in option pricing has not been incorporated into fast Fourier Transform of both European and American-style options. Very few authors have worked on Fourier Transform of American-style options compare to European style options. The notable one known to us as at the time of this research was the work of Oleksandr, Z. in (2010) [31] . Geske-Johnson scheme with Richardson Extrapolation was adopted to numerically extend fast Fourier Transform algorithm to American-style security, which features a continum of potential exercise times up to expiration.
Our contribution to the existing literature on options valuation is highlighted in sequel:
1) We incorporate economic recession induces volatility uncertainty into exponential jump model with stochastic volatility and intensity. The economic recession induce volatility is assumed to be an uncertain variable.
2) Derivation of Characteristic function of the affine model with recession uncertainty effect is presented.
3) The Fourier transform of the affine model is performed.
4) The Characteristic function of the affine model is extended to fast Fourier transform algorithm of Carr & Madam [29] in pricing European options. It was extended to pricing American style options by adding time premium such that the limit value tends to zero at the expiry time.
5) Volatility Surface of the affine model based on the recession induced uncertainty is presented.
2.2. Uncertainty
Definition 1: [5] [6] . An uncertain variable
is a measurable function from an uncertainty space to the set of real numbers.
Definition 2: O.O. Ugbebor [6] . Let
be a non-empty set. A collection
consisting of subsets of
is called an algebra over
if the following three conditions hold:
•
;
• if
, then
; and
• if
, then
Under the notion of countable union, if
such that
the collection
becomes a σ- algebra over
.
Example 1: Suppose
is a proper subset of
. Then the set
is a σ-algebra over
.
Remark 1: The collection
is closed under countable union, countable intersection, difference and limit.
Definition 3: [5] [6] Let
be a non-empty set and suppose
is a σ-algebra over
. Then
is called a measurable space and any member in
is a measurable set.
Definition 4: [6] A function
is said to be measurable if
(1)
where
is a measurable space and
is a Borel set of real numbers.
2.3. Uncertain Measure
B. Liu, [4] [5] highlighted the following three axioms for an uncertain process:
Axiom 1: (Normality Axiom);
for the universal set
.
Axiom 2: (Duality Axiom):
for any even
.
Axiom 3: (Subadditivity Axiom);
for every countable sequence of events
.
Remark 2:
For some application of B. Liu (2007)’s uncertainty theory, the reader should see the research work of the following authors in [12] [13] [14] as cited earlier.
2.4. Fourier Transform
Fourier transform in mathematical finance was firstly used to determine the distribution of an underlying asset price under the stochastic volatility model by the inversion method, Stein et al. (1991) [18] . The following definitions and conditions are necessary for the understanding of Fourier transform technique.
Definition 5: Let
be a Lebesgue-measurable function of
, then the
-norm of f is defined by
(2)
where
(3)
Equivalently,
is a piecewise integrable real function over the entire real line satisfying the condition
(4)
For the Fourier transform and inverse Fourier transform of a function to exist, it is necessary that the function is absolutely integrable over R with finite value as defined in (3) above. An absolutely integrable functions on a given interval
are said to be on the space of
. The notion of Fourier transform can be extended to the square integrable functions.
Definition 6: A square integrable functions is defined by
(5)
The space of square integrable functions is represented by
over the real line or simply an interval
.
Definition 7: Let
be a real-value function for
, then the Fourier transform of f is defined as
(6)
where
and
is a parameter.
We can recover
from
by the inverse Fourier transform.
Definition 8: The inverse Fourier transform of the real valued function
is defined by
(7)
which belongs to either
or
- spaces.
3. Accounting for Jumps in the Asset Prices Linked with Recession
The major market parameters which most financial modeler will wish to consider while formulating a financial model relies on price, interest rate, dividend rate, volatility and time. In an economy threatened by recession, asset price tends to experience lots of fluctuation. Asset price especially stocks can never be stable. It is very necessary to consider interest rate and volatility to be stochastic in nature. Even if one considers interest rate to be constant, in reality volatility cannot be constant. The Stock volatility is seen as a measure of the uncertainty on the payoff or returns of the stock which investors look up to for decision making and taking. During economic recession, the rate of volatility variation is considered higher than the state of normalcy of an economy. As a result an economy recession factor is invoked in this paper as we shall see later.
Jumps in the Underlying Stock Price
Consider the dynamics of a stock price
given by
(8)
where r is the interest rate, q is the dividend rate,
is a Poisson process with stochastic intensity
, m is an average jump amplitude given as
where jump size
is a random variable. The equation consists of diffusion process and jump process. There are two sources of fluctuations in the stock price which we classified as “changes in economic state” and “changes due to supply and demand factors”. The inclusion of jump in the model is to cater for the arrival of useful information into the market that will have an abnormal consequence on the stock price. Among the factors that are responsible for jumps in the stock price highlighted by Matthew, S.M in [32] , we added economic recession factor. The factors are grouped into:
• Firm specific jumps: Caused by news inflow to the market on individual firm’s profit/loss report.
• Industry/sector specific jumps: Caused by news that can affect specific company or industry such as news on sudden declaration of Holiday.
• Market specific jumps: This jumps are caused by news such as oil prices, interest rates, credit spreads etc. that affect the market.
• Economic recession jumps: This is caused by the news inflow to the market on the state of the economy to include deep economy crisis with recession probability indicators.
In our model formulation of stock price to capture economy recession induced volatility uncertainty on stock in the next section, we further grouped the above highlighted factors “(a)-(c)” as other sources with volatility
while the factor (d) Economic Recession induced volatility source as
.
Poisson process
has probability density function given as
(9)
where
is the intensity. In line with Matthew [24] , if information on economic recession or other source of panic enters the financial market (stock) causing an instantaneous jump in the stock price such that the price jump change from
where
is taking as the absolute magnitude jump. Then the relative change in price is given by
(10)
4. The Model Formulation
Let
be an economy recession induced parameter variation define on an uncertain space
, with
such that
Then
(11)
is an uncertain variable. We have that
and
such that
.
Example 2: Let the above economic recession induce parameter variation
defined on an uncertain space
, with
be defined such that
satisfying Equation (11), then
and
Let
be a filtered probability space where
and
describes the filtration in the market and the economy where market activities takes place, respectively. The
and
are the market information and economy information available up to a time
respectively.
Definition 9: [33] An uncertain random variable is a measurable function
(resp.
) from an uncertainty probability space
to the set in
(resp.
), for any Borel set
(resp,
) the given set
.
The expected value of the uncertain random variable
is defined as
(12)
where
and
represent the expected values under the uncertainty space and the probability space, respectively.
The above definition connects both the notion of probability and uncertainty such that the random variable is defined from a probability space to uncertainty space. It makes sense to introduce the notion of uncertainty to financial models especially while pricing during economy recession or strong financial crisis in the market. The works of the authors cited in this paper to have contributed to parameter uncertainty in financial models did not consider uncertainty with respect to economic recession. We extended the notion of uncertainty to the term structure of stochastic volatility to include economy recession.
Let an asset X be described as a two-state regime switching process which is free to jump between the states defined as
(13)
Suppose further that there is room for transition between the two states which evolves as a Poisson process
(14)
where
is the rate of transition from state l to state m and the times spent in state l before transiting to state m is
.
Assumption 1: Assume there are two sources of volatility on the asset,
, i.e volatility
and
representing market volatility triggered by economy recession and other sources (usual) respectively such that
, but
(15)
Assumption 2: It is assumed that an economy cannot be in the two states at the same time. Therefore, when pricing in the financial (stock) market, the choice of the volatility parameter depends on the state of the economy. For example, if the stock is under the exposure of economy recession, then market volatility of the stock
since recession will have an influence on the market but if there is no recession, then market volatility
usual volatility, here
, since
.
Suppose further that the asset X price is defined on a filtered probability space
such that the market filtration is generated by the combination of Wiener process and jump process at a given time,
and
is taken as a risk-neutral probability measure. The dynamics of the underlying stock price
(not necessarily a stock) is given by
(16)
where r is the interest rate, q is the dividend rate,
is a Poisson process with stochastic intensity
, m is an average jump amplitude given as
where jump size
is a random variable. The parameters
and
are constants with mean - reverting rates
and
which are also taken to be positive constants. The stock market stochastic volatility
(17)
where
is economy recession induced volatility in the stock market due to the information flow from the Recessed Economy into the stock market while
is the volatility in the market from other sources. Furthermore, the constants
and
are respectively regarded as the usual long-term volatility, long-term volatility influenced by recession during the period of economy recession and
is the intensity constant. The
as specified above is to account for the possibility of economy recession source of long-term volatility in addition to the usual long-term volatility that may arise during the life-span of the quoted option on the stock. Also,
and
are Wiener processes but
evolve independently of the correlated Wiener process
and
in the above model. The correlation of
and
is such that
with
is less than 1. As we take m to be an average jump amplitude since the stock price is expected to jump either upward or downward. Then setting
(18)
where p is the probability of upward move jump and q, the downward move jump such that
. In [16] , the mean positive jump and negative jumps
were given as
and
, respectively. An analysis on double exponential
jump model with stochastic volatility and stochastic intensity was done by Jiexiang Huang et al in [34] and solved. The major distinction between our formulation here and that of [34] is the incorporation of economic recession induced uncertainty into the term structure of the volatility of the model. Consequently, we propose the model in Equation (16) to be referred to as an “Uncertain Affine Exponential jump model with Recession induced Stochastic volatility and stochastic Intensity”.
Remarks 3:
The stochastic volatility
of the stock has been formulated to capture recession induced volatility.
4.1. Determination of Characteristics Function
The notion of characteristics function is indispensable in the study of random variables in the context of jump diffusion processes. It is a viable tool in Fourier transformation of options pricing. It is worth noting that the distribution function of jump diffusion processes in closed form may not be readily available or known but the characteristics function is explicitly known. However, the characteristics function of some certain stochastic processes or model may not be readily available in closed form but it can be determined.
Definition 10: The characteristics function of a random variable X is a function
(19)
where
is the probability density function of the random variable X.
This definition almost coincide with the definition of inverse Fourier Transform in (6) with the exception of
. For a Poisson process say
with
parameter
, the characteristics function is given by
(20)
There is relationship between Moment-generating function and characteristics function. Moment generating function say, M of a real valued random variable is very useful in the study of probability theory as an alternative specification of the probability distribution of the random variable
.
Definition 11: Moment-generating function of a random variable, X, is defined as
(21)
if the expectation exists.
Example 3: For a Poisson
distribution, the moment-generating function
and its characteristic function
.
For a continuous probability density function, the moment-generating function is
(22)
where
is the probability distribution function.
To this end, let
with
or
as the case may be where
is the log stock price in the model (16) and
is the time difference between the maturity time and the present time or the time difference between the optimal time and the present time for exercising the option as the case may be. The latter is for Early exercise of American option peradventure one is able to determine the optimal exercise time for the option. In order to derive the characteristics function for the proposed model in 16, we need to consider Feynman-Kac Formula in what follows.
4.2. The Feynman-Kac Formula Revisited
The formula states that a probabilistic expectation wrt some Ito-diffusion processes can be obtained as a solution of a related partial differential equation. For an example, for a 1-dimensional stochastic process
which is a solution of stochastic differential equation
where
are Wieners process with correlation
. Let
be some payoff.
Then the function
(23)
is a solution of the PDE
(24)
with final condition
. For 1-dimensional stochastic process Xt which is a solution of the SDE
(25)
By Feynman-Kac formula, for any function say
(26)
is the solution to the PDE
(27)
The Equation (26) is useful as it can be extended to characteristics function as
(28)
Similarly,
(29)
Remarks 4:
1)
is the characteristics function of
.
2) The moment-generating function
.
4.3. Solution to the Proposed Uncertain Affine Exponential Jump Model with Recession Induced Stochastic Volatility and Intensity
Consider the Equation (16) rewritten in the form
(30)
where
and
and the volatility is taken as
as defined in Equation (17). The PIDE for the moment-generating function
of
for the model above is given by
(31)
where
is the final condition and
.
The solution to the PIDE (30) is speculated to be of the form
(32)
Substituting Equation (32) into (31) gives
(33)
Rearranging the equation in terms of the state variables volatility and intensity results to
(34)
where
(35)
is the moment-generating function of the jump size distribution and m is an average jump amplitude given earlier by
(36)
Equating the coefficients of the term structures (the stochastic volatility and the intensity) in Equation (35) to zero, the following ordinary differential equations were obtained:
(37)
(38)
(39)
The above systems of solutions were solved as follows.
Starting with the Equation (38) first, we can see that Equation (38) is a Ricatti differential equation. Setting
(40)
in Equation (38) and simplify further, one will have a second order differential equation given by
(41)
The general solution of the Equation (41) is given by
(42)
where
(43)
At
, the following boundary conditions hold:
(44)
The sum
with
and the product
The constants
and
has values
and
respectively using the boundary conditions in Equation (47) and initial conditions
Substituting for
and
in Equation (40)
and after simplification gives
(45)
(46)
In line with Artur [35] . Letting
.
We rewrite Equation (37) as
(47)
such that
(48)
(49)
Integrating the Equation (48) firstly, the following equations emerged.
(50)
(51)
(52)
(53)
(54)
(55)
The result is finally written as
(56)
Similarly, integrating the ODE in the Equation (49), one will have
(57)
Writing an explicit solution for
as the sum of the solutions
and
in (56) and (57) respectively yield
(58)
Analogously,
(59)
where
(60)
(61)
(62)
(63)
but
The summary of the solution to the model (16) in which we have incorporated economic recession induced volatility parameter on the stock market price is given by the characteristic function approach (the core for Fourier transform) in sequel as
(64)
where
For a financial claim
satisfying the Partial Integro-Differential Equation (PIDE) given in Equation (30) such that the payoff function say
is satisfied by the claim, i.e.
. The Fourier transform of
simply put defined on the PIDE in the light of the definition defined in Equation (5) is given as
(65)
and the corresponding inverse Fourier transform using definition in (6) is given by
(66)
In light of Theorem 3.1 given by Artur Sepp [35] , and Theorem 3.2 given by Lewis (2001) [36] on page 11, we gave another modified version as follow.
Theorem 5: (Characteristic formula)
Let an asset price
possesses an affine analytic characteristic function
at time
. Define a regularity strip
where
is the imaginary part of w lying between
and
in the regularity strip. Suppose further that
is defined on space of
such that
where
is the payoff strip and
obeys the Fourier transform given in Equation (65). Then the option value is given by
(67)
where
.
Proof:
In a risk-neutral world Q, we expressed
(68)
(69)
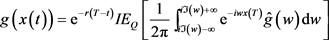 (70)
(70)
(71)
(72)
Corollary 6 : (Characteristic formula for early exercise Option)
For an American option, consider a range of time
, where t is the initial (starting) time,
is an early exercise time and T is the expiry time. Suppose one is able to determine an optimal payoff time
in a stopping region, then the early exercise payoff of the claim
is given as
(73)
whenever
.
The proof follows immediately from the above theorem in addition to optimality condition attached to early exercising of American options whenever the early exercise time
.
The justification of the corollary rely on the fact that an American option can be exercised at any time up to the expiry time. By symmetric property, we assume that there exists
since
, and by extension the entire integrand exists whenever
.
5. Numerical Fourier Based Transform of
A good number of references such as Carr & Madan (1999) [29] among others has agreed that if the corresponding characteristic function of a risk-neutral density is given or derived, the Fourier transform representation can be written analytically.
Let the characteristics function
of the moment generating function
derived above holds for the affine model. In general, we rewrite
(74)
where
:= Optimal time in the time horizon
.
In the case of European call
maturing at time
with exercising price
defined on an underlying stock S. Suppose further that
represent the probability distribution function pdf of
. Then the fair price
is expressed as the present value of the expected payoff defined by
(75)
With reference to Carr & Madan (1999) [29] , we rewrite modified call to accommodate damping factor say
so that
.
Define
as the Fourier transformation representation of
such that
. (76)
Then the call option price function is written as
(77)
(78)
in (78) is the Fourier transform of the call price given by
(79)
(80)
(81)
(82)
Integrating the term in the second integral wrt k gives
(83)
Further simplification yields
(84)
By rationalising the base yields
(85)
(86)
From difference of two’s squares, the denominator reduces to
(87)
Since
, then negative sign in the denominator changed to positive,
Hence we have
(88)
a and b as used above are for ease simplification purpose and henceforth suppressed.
(89)
Finally,
(90)
Substituting Equation (90) into (79), we now have a complete analytical formula for the option price as
(91)
Equivalently stated as
(92)
Extending this formulation to American option, we express the value of American call price as the sum of European call Fourier prices and Early exercise premium price as
(93)
represent the early premium price of the American call option such that
, since at the maturity time, continuation region varnishes and there is no waiting time any longer. In other words, once the option reaches the maturity date, if it has not been exercised at an early time
, then the option must be exercised at
. The implication is that the American option prices coincides with that of European option prices at the maturity date, T.
Hence,
(94)
To extend FFT algorithm which is a numerical technique of Discrete Fourier Transform (DFT) to American options valuation for the models under study with economic recession induced uncertainty, we define Fast Fourier Transform (FFT) equation as
(95)
Applying FFT algorithm to (94), we have
(96)
where
,
and
.
is the size of consistent spacing existing between N values of log strikes K. Setting
, and substituting into Equation (96) yields
(97)
The size of the consistent spacing
between the N values of k has the following relation
(98)
The relation is observable if we make comparison between Equations (95) and (97).
The smaller the values assumed by
, the better the fineness of the integration grid and vice versa.
Numerical Experiment
Consider an American Stock with initial price
, Strike Price
, Risk free interest rate
, Dividend rate
, Time to Maturity
year, Volatilities
, Integrability Parameter
, Fineness of integration grid point
. The call option value on the underlying American stock is reported below.
Table 1 above shows the payoff of a dividend paying American style call options during economic recession period and recession free period in Nigeria which the proposed volatility change formulation presented in this paper stressed. The option prices obtained via Fast Fourier Transform (FFT) approach yields better results compared to the values obtained by BSM and American call options solver prices. This confirmed numerical performance of Fast Fourier Transform (FFT) technique among other methods of pricing options such as Analytical payoff via BSM and American call option solver.
Figure 1 shows the true representation of the call options value obtained during recession free period in Table 1 above while Figure 2 shows the payoff of the
![]()
Figure 1. FFT call options payoffs comparison among other methods without recession induced volatility.
![]()
Table 1. Numerical value for a dividend paying American call options.
![]()
Figure 2. FFT call options payoffs comparison among other methods with recession induced volatility.
American style call options during recession period. The inference we can draw from both the Table 1 and the two Figure 1 and Figure 2 is that during a very short maturity period of a month in the options life span, the options value in both economic states (recession and recession-free) coincides while as the maturity period increases beyond a month, the upward volatility change induced by recession causes slight increase in the call options prices. If further experiment is carried out on put options, reverse will be the case in terms of volatility change effect on the put options payoff.
6. Conclusions
The notion of economic recession and its effect on volatility uncertainty on the payoff of European and American Options based on some certain assumptions was presented in this paper. Economic recession is becoming a global issue and not too far to be recognized as a re-occuring incident. In the history of economic recession, US is at the forefront as the continent has experienced several economic recessions. An intuition behind the introduction of economic recession induced volatility uncertainty in this research could be traced to Nigeria economic recession outbreak in 2016. This has an enormous effect on investors, financial institutions and every other economic activities in the country and by extension affected some aspect of foreign transactions (exchange), import and export etc. by the individual within and outside the country. In relation to the options (or stock) market, volatility has been a reference point to the level of fluctuation in the market price of the underlying asset. It is seen as a metric for the speed and amount of changes stochastically in the underlying asset’s prices. An investor’s acquaintance with volatility gives a better comprehension of why option prices behave in certain ways and this will guide them in decision making.
The model we investigated is proposed to be referred to as Uncertain Affine Exponential jump model with Recession induced Stochastic volatility and Intensity. Fourier transform of the model was implemented having derived an affine close form of the characteristic function. A numerical based Fourier transform algorithm called Fast Fourier transform (FFT) which was a variant of Carr & Madan [29] FFT algorithm for European call option valuation was adopted to determine the European call Fourier prices. The algorithm was further extended to American call options valuation by adding premium price to the European call options prices.
We also reported Nigerian Flourmill stock performance, during recession and recovery year in this study. The Stock volatility is seen as a measure of the uncertainty on the payoff or returns of the stock which may require an estimation. The two common methods in practice for an estimation of volatility of stocks or assets generally are known to be an estimation of historical volatility or implied volatility on that stock. Estimation of Recession induced volatility may be difficult to be determined accurately. Nevertheless, the fact we try to establish here is that the stocks price experiences a high level of uncertainty during the period of recession. The volatility of stocks tends to increase during recession compared to the period of normalcy. One major point is that volatility is never constant in an ideal real life situation. The Flourmill stock prices data used for calibration purpose revealed that during Nigerian recession, the stock prices became more volatile compared to other periods. According to the Assumption 1 above in this paper, we suggest the use of historical data prior to recession period to determine the level of uncertainty posed by Economic recession which we refer to as Economic recession induced volatility. We hope the figures we generated using MATLAB was presented in the Appendix section. Figures A1-A5 showed more details in terms of volatility change effect on stock prices induced by economic recession.
Acknowledgements
The authors would like to thank the editors and the anonymous reviewers for their useful comments and suggestions.
Appendix
The following Figures A1-A5 were generated using Nigerian Flour mill stock prices of year 2016-2017 through MATLAB.
![]()
Figure A1. Nigerian flourmill stock prices movement during recession 2016 and recovery year 2017.
![]()
Figure A2. Comparison of stock prices variance during Nigeria economic recession.
![]()
Figure A3. Bar charts of flourmill stock prices movement during Nigeria economic recession and recovery year.
![]()
Figure A4. Flourmill stock price metrics during economic recession period.
![]()
Figure A5. Rotated side view of flourmill stock prices metrics during Nigerian economic recession 2016.