Slipping Phenomenon in Polymeric Fluids Flow between Parallel Planes ()
1. Introduction
Many fluid systems, including polymeric materials, reveal the anomaly of slipping often near the solid surface. The presence of such a wall effect leads to a violation of the hypothesis on attachment and the need to specify appropriate boundary conditions.
This anomalous behavior of materials in a plastic state (slurry, grease, fluids and polymer melts) at solid surfaces requires a comprehensive study of both rheological properties and calculating the flow parameters and characteristics of the processing equipment. In the first place, there are rather complex problems of determining the rheological characteristics of the material results according to the viscometric studies. The next stage is associated with specific problems on the motion of fluids which exhibit abnormalities in solid surfaces and the direct use the sliding velocities as boundary conditions.
It should be noted that the study of this issue is reviewed in a large number of papers in [1], where it was noted that there are two approaches to study of this phenomenon.
The first approach is a detailed study and consideration of molecular properties of contacting media, the formulation of a mechanism of slippage and checking the adequacy of the proposed approach. Moreover, the results for different physical systems have much in common, which indicates the possibility of a unified approach to the study of this effect.
The second approach is to specify explicitly the slip velocity at the wall – , which is generally a function of stress at the wall –
, which is generally a function of stress at the wall – , the geometric dimensions and temperature. And this dependence of slip velocity at the wall of these factors can be found from viscometric measurements [1].
, the geometric dimensions and temperature. And this dependence of slip velocity at the wall of these factors can be found from viscometric measurements [1].
From the mathematical point of view, the result of each approach leads to dependence – , and this dependence is taken from the processed experimental data. At the same time as an argument, you can choose not only –
, and this dependence is taken from the processed experimental data. At the same time as an argument, you can choose not only – , but the pressure gradient and the specific consumption and the choice of a particular function in the study depending on how easily one can apply the law in the calculations.
, but the pressure gradient and the specific consumption and the choice of a particular function in the study depending on how easily one can apply the law in the calculations.
2. Rheological Model
In modeling the flow of solutions and melts of linear polymers formulating rheological constitutive relations plays an important role. It establishes the relationship between the kinematic characteristics of the flow and internal thermodynamic parameters. Previously a simple rheological model based on microstructural representations [2,3] was proposed
 (1)
(1)
where —the stress tensor; p—hydrostatic pressure,
—the stress tensor; p—hydrostatic pressure,  and
and —the initial values of the shear viscosity and relaxation time,
—the initial values of the shear viscosity and relaxation time,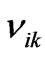 —the tensor of velocity gradients;
—the tensor of velocity gradients; —symmetric second rank anisotropy tensor;
—symmetric second rank anisotropy tensor;  —the first invariant of the anisotropy tensor,
—the first invariant of the anisotropy tensor,  —the symmetrized velocity gradient tensor,
—the symmetrized velocity gradient tensor, —phenomenological model parameters that take into account in the equations of the dynamics of the macromolecule size and shape of the molecular coil. This model was tested for compliance by viscosimetric flow of real polymeric liquids [2-7] and by calculating the overlap of small oscillatory fluctuations in simple shear flow in the parallel and orthogonal shear directions [7]. In conducting the numerical experiment dependences on the stress tensor of velocity gradients and from time to time were obtained, allowing for calculations of the complex shear modulus, dynamic viscosity and dynamic loss angle depending on the frequency of forcing oscillations, shear rate and the number of Deborah (De). The dependences obtained are compared with experimental data that showed qualitative compliance between theory and experiment.
—phenomenological model parameters that take into account in the equations of the dynamics of the macromolecule size and shape of the molecular coil. This model was tested for compliance by viscosimetric flow of real polymeric liquids [2-7] and by calculating the overlap of small oscillatory fluctuations in simple shear flow in the parallel and orthogonal shear directions [7]. In conducting the numerical experiment dependences on the stress tensor of velocity gradients and from time to time were obtained, allowing for calculations of the complex shear modulus, dynamic viscosity and dynamic loss angle depending on the frequency of forcing oscillations, shear rate and the number of Deborah (De). The dependences obtained are compared with experimental data that showed qualitative compliance between theory and experiment.
Also on the basis of the rheological model (1) seconddary flows in rectangular channels were calculated. Paper [5] considered the steady flow in a smooth round pipe under constant pressure gradient. The system of equations for solving the complete hydrodynamic problem was recorded in a cylindrical coordinate system.
In this paper we will solve the problem of determining the velocity profile of a nonlinear viscoelastic fluid moving between parallel planes under a constant pressure gradient: , based on model (1). We arrange the origin of one of these planes, axis
, based on model (1). We arrange the origin of one of these planes, axis  directed along the flow, axis
directed along the flow, axis —perpendicular to the plane and axis
—perpendicular to the plane and axis —perpendicular to axes
—perpendicular to axes  and
and .
.
Then the system of equations of dynamics in Cartesian coordinates will be:
 (2)
(2)
where: ,
, ,
, —velocity along the axes
—velocity along the axes ,
, and
and 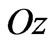 respectively,
respectively, —the density.
—the density.
Since along axis  velocity profile will not change, the final expression does not depend on the variable z and the system of Equations (1) and (2) becomes:
velocity profile will not change, the final expression does not depend on the variable z and the system of Equations (1) and (2) becomes:


 (3)
(3)
The system of Equations (3) describes the flat twodimensional unsteady flow of polymer media. Further, we find independent of variable x solutions of the system and we obtain:
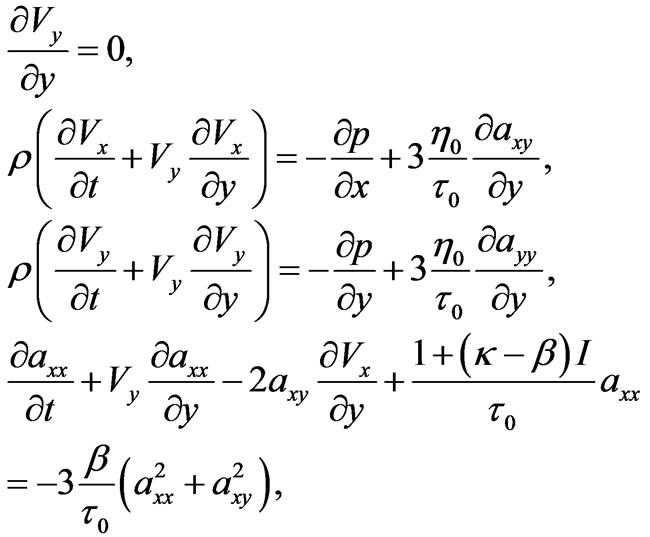

 (4)
(4)
The first Equation (4) implies that —linear function y, but due to boundary conditions:
—linear function y, but due to boundary conditions: 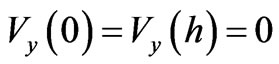 , which shows that:
, which shows that:  and the continuity equation is automatically satisfied. Given this, Equation (4) can be rewritten as:
and the continuity equation is automatically satisfied. Given this, Equation (4) can be rewritten as:



In the stationary case we have:

 (5)
(5)
In [6], the system of Equation (5) was solved by successive approximations method up to the first order in the parameters of the induced anisotropy, and obtained the following expressions for the components of the stress tensor and the longitudinal velocity components:


 where
where 
Second Equation of (5) shows that non-zero pressure gradient in the direction perpendicular to the flow velocity is found. However, that does not lead to the emergence of secondary flows. This pressure gradient may be due to the effect of swelling of the jet at the exit of the channel. The expressions obtained due to approximation can not be used for large pressure gradients that are of interest in practice, therefore we will be selins depending on the expressions for the components of the stress tensor and the components of the velocity without the smalllness of the model parameters. Then out of the first equation of system (5) we have:
 (6)
(6)
This shows that the shear stresses for two dimensional steady flow is a linear function of the variable, and the constant of integration is chosen from the condition of symmetry: For clarity, we introduce the following notation:
 (7)
(7)
Then the system of Equations (5) becomes:
 (8)
(8)
Subtracting the first Equation (9) the last equation, after transformations we obtain:
 (9)
(9)
The second Equation of (8) can be rewritten as:
 (10)
(10)
Then dividing (9) to (10) we obtain:
 or
or  (11)
(11)
Substituting (11) in the last Equation (8) we obtain an equation containing only variable that, once converted in the form:
 (12)
(12)
Equation (12) can be solved by one of the iterative methods, such as the method of successive approximations, and taking into account the expression (6), we can find the dependence: that is, by virtue of (11) and (10) leads to dependence and. Next numerically integrating, using (7) and using the boundary condition the dependence can be found.
3. Results
It turns out that as an additive constant of integration, the total flow rate will have the form

where —the additional flow rate calculated under the condition at the wall sticking. If we assume that
—the additional flow rate calculated under the condition at the wall sticking. If we assume that  is a function of
is a function of —the stress at the wall, when calculating the velocity profile becomes necessary in an iterative procedure for approval
—the stress at the wall, when calculating the velocity profile becomes necessary in an iterative procedure for approval  and
and .
.
If we assume that  is a function of the
is a function of the , then this procedure isn’t necessary to carry out The dependence
, then this procedure isn’t necessary to carry out The dependence  can be easily obtained by processing experimental data, as done in Figure 1 for data from [9], where melt flows polyethylene high and low density were studied. These melts are extruded through the die width of 1 mm and it was found that low-density polyethylene adheres to the interface, high-density polyethylene shows slippage at the wall. For the sliding velocity by the following relation was obtained:
can be easily obtained by processing experimental data, as done in Figure 1 for data from [9], where melt flows polyethylene high and low density were studied. These melts are extruded through the die width of 1 mm and it was found that low-density polyethylene adheres to the interface, high-density polyethylene shows slippage at the wall. For the sliding velocity by the following relation was obtained:

Values themselves were determined by the formula: .
.
Note that the data for low density polyethylene have been described based on the approach (1) in [8].

Figure 1. Approximation of experimental dependence of the slipping velocity at the wall on the additional flow rate.
Let us now consider how to influence the parameters of the model, and the type of derived dependencies. To this end, fix scale parameters, and (in this case), and will take into account that in many cases, as shown in [7]. The results are shown in Figure 2, which shows the flow of the pressure gradient for different values and which shows that increases with increasing deviation of the flow from the law of Poiseuille, as appropriate . In this case, the dependences of the accounting slip appears a kink, which is associated with an approximation used for Figure 1. The curves corresponding accounting slip located above the curves are constructed by taking into account the slip at the wall.
. In this case, the dependences of the accounting slip appears a kink, which is associated with an approximation used for Figure 1. The curves corresponding accounting slip located above the curves are constructed by taking into account the slip at the wall.
In order to allow comparison with experimental data [9], we note that in [9,10] there are no data on the values of the pressure gradient and therefore its definition should be used according to Figure 2 and the known values of flow rate to determine the value of the pressure gradient and then using it to calculate the velocity profiles. Comparison of experimental and theoretical curves for the velocity profile in the gap between the parallel planes are shown in Figure 3.
Thus, in considering the case of plane Poiseuille flow with allowance for slippage of the polymer material at the boundary, the system of equations of the modified model Vinogradov and Pokrovskii describes non parabolic velocity profile in the gap between parallel plates, which is confirmed by experimental data. Dependence obtained in this can be used to develop numerical methods for 2-dimensional and 3-dimensional flows as an initial approximation of input and output profiles in the simulation of flows of polymer fluids in the gap between parallel planes, for example, when forming thin films.

Figure 2. Dependence of flow on the pressure gradient in different flow regimes in the presence of stick and slip phenomena.

Figure 3. Comparison of experimental (points) and theoretical dependencies of the velocity profile in the gap for different values of specific consumption.
5. Acknowledgements
The authors greatly appreciate Prof. Vladimir Pokrovskii for his interest to this work and useful discussions.
NOTES