A Knowledge Measure with Parameter of Intuitionistic Fuzzy Sets ()
1. Introduction
Entropy is a basic parameter that characterizes the state of matter launched by Shannon [1] , which is used to characterize the degree of disorder in the system, the uncertainty of the system structure and movement, and the degree of irregularity. In 1965, Zadeh launched fuzzy sets (FS) [2] , and Atanassov proposed intuitionistic fuzzy sets (IFS) in 1986 by introducing the degree of hesitation, which means that the research of intuitionistic fuzzy sets is more complex than that of fuzzy sets [3] . Fuzzy entropy is one of the most important methods to measure the degree of disorder in fuzzy sets, and knowledge measure is one of the most important bases for measuring the degree of order between fuzzy sets [4] [5] [6] . In 1972, De Luca and Termini put forward an axiom system of fuzzy entropy in terms of Shannon’s entropy function [4] [6] ; Yager proposed some fuzzy entropy formulas according to fuzzy distance measure [5] . Since then, many scholars began to use various methods to study fuzzy entropy and intuitionistic fuzzy entropy [6] - [11] . Because intuitionistic fuzzy sets are an extension of ordinary fuzzy sets, many scholars focus on entropy and knowledge measure of intuitionistic fuzzy sets [7] - [16] . In the past 20 years, based on the study of fuzzy sets, many scholars have proposed a variety of methods to calculate intuitionistic fuzzy entropy and knowledge measure [7] - [16] . Based on the axioms of intuitionistic fuzzy entropy [10] [11] , Szmidt and Kacprzyk presented a standard judgment of intuitionistic fuzzy knowledge measure with a relatively wide application [12]: non-negative boundedness, symmetry and order. Some researchers also studied Szmidt and Kacprzyk’s axiom system and introduced some classic knowledge measure formulas [13] [14] [15] . According to the order property, Guo put forward a new knowledge measure with order [13] , Nguyen presented a model from a classic distance measure [14] , and Das et al. proposed a new model based on a series of similarity measures [15] . However, most of the existing research only focused on knowledge measure based on membership degree and non-membership, lack of the research of the known extent for information amount. In order to make full use of intuitionistic fuzzy information to construct information measurement tools, this paper studies a fractional knowledge measure.
Taking into account the extensive application and its rationality of the axiom system by Szmidt and Kacprzyk [12] , we first put forward a simple necessary & sufficient condition of order property in Section 2. And then, we comprehensively analyze the differences among some classic models of intuitionistic fuzzy knowledge measure. Hence, in Section 3, we bring about a new construction method consisting of the decision-making advantages and the known extent and theoretically prove that this knowledge measure satisfies all the conditions of Szmidt & Kacprzyk’s axiom system. It is proved theoretically that the operators with the order condition in Szmidt & Kacprzyk axiom system will be better than those without the order condition. In Section 4, combined with the research results of De et al. [17] , an experimental case construction and empirical test scheme are put forward. Experimental results show that the performance of the presented model with parameters is better than that of the majority of classical operators, and the operators with the order condition will be more accurate than those without the order condition.
2. Intuitionistic Fuzzy Sets
Definition 1 An fuzzy sets (FS) A in a finite set X is an object with the following form:
where
,
.
where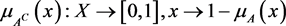 .
.
Definition 2 An intuitionistic fuzzy sets (IFS) A in a finite set X is an object with the following form:
and
are the degree of membership and non-membership, respectively.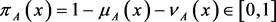 ,
is the degree of hesitancy.
,
is the degree of hesitancy.
Definition 3 Let A and B be two IFSs, then we have:
1)
if and only if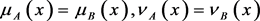 .
.
2)
if  and
and .
.
3) .
.
3. Entropy and Knowledge Measure of IFS
Claudius’s entropy is one of the important parameters in physics that characterize the state of matter. It is a measure of the degree of chaos in the physical sense and describes the disorder degree of matter in an isolated system. In 1948 Shannon first launched entropy into information theory in the “Mathematical Principles of Communication”, which characterize the degree of disorder, and uncertainty and irregularity of system structure and motion [1] . After the creation of fuzzy sets, many scholars proposed a series of fuzzy entropies and its formulas, which are used to express fuzzy uncertainty. Since Atanassov proposed intuitionistic fuzzy sets [3] , many scholars presented many intuitionistic fuzzy entropy formulas and knowledge measures [7] - [16] . Next some classic entropy formulas and their knowledge measures will be introduced.
Fuzzy entropy is defined as follows [4] [5] [6]:
Definition 4 A fuzzy set A in the domain X, for each
,
is the entropy of A with the following properties:
(EP1)
or
.
(EP2)
.
(EP3)
.
(EP4) For another fuzzy set B,
denotes the entropy of B, and then we have: If
and
,
; If
and
,
.
where
and
are the degree of membership of fuzzy sets A and B, respectively. EP1 and EP2 denote the property of non-negative boundedness, EP3 is the property of symmetry, and EP4 is the property of order.
Intuitionistic fuzzy entropy is defined as follow [7] - [11]:
Definition 5 For IFS A in the domain X,
is the entropy of A with the following properties for
:
(EP1)
or
.
(EP2)
.
(EP3)
.
(EP4) For another IFS B,
denotes the entropy of B, and we have: If
and
,
; If
and
,
.
Where
are the degree of membership, non-membership and hesitancy of IFS, respectively.
EP1 and EP2 are the property of non-negative boundedness, EP3 is the property of symmetry, and EP4 is the property of order.
In terms of EP4, we obtain the following necessary and sufficient conditions:
(EP4I)
If
or
, then we have
.
Proof.
, and
, then
.
And if
, then we have:
,
and then we get
and
.
Similarly,
, and
, then
.
And if
, then we have:
, and then we have
and
.
EP4 is equivalent to EP4I, thus we obtain
.
According to Definition 5, intuitionistic fuzzy knowledge measure can be defined as follows [12] [13]:
Definition 6 For IFS A,
is an intuitionistic fuzzy knowledge measure of A if
have the following properties:
(KP1)
.
(KP2)
or
.
(KP3)
.
(KP4) If B is also an IFS, and
is the intuitionistic fuzzy knowledge measure of B, then we have: If
and
,
; If
and
,
.
KP1 and KP2 are the property of non-negative boundedness, KP3 is the property of symmetry, and KP4 is the property of order.
In terms of EP4, we obtain the following necessary and sufficient conditions KP4I:
(KP4I)
If
or
, then we have
.
Obviously, KP4Ⅰmeans that for
, we infer
. Hence, knowledge measure
can be considered to be a positive relation to
.
From the concept of entropy and knowledge measure above, we can define the knowledge measure of IFS A by:
(1)
Some intuitionistic fuzzy knowledge measure formulas can be defined according to some classic intuitionistic fuzzy entropy formulas as follows:
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
In 1996, Bustince and Burillo proposed an entropy formula
[7] . In 2014, Szmidt and Kacprzyk introduced an improved knowledge measure formula
, which is derived from the entropy
[12] . In terms of the Szmidt and Kacprzyk’s axiom system [10] [11] [12] , in 2016 Guo put forward
, which is the basis of
[13] . Moreover, Huang and Yang presented
and
in 2006 [9] . In [14] , Nguyen introduced a knowledge measure formula
according to distance measure proposed by Szmidt and Kacprzyk [18] , and Szmidt and Kacprzyk presented a knowledge measure
from similarity measure [16] . Both
and
are proved to be equivalent to knowledge measure
introduced by Das, Guha, and Mesiar [15] .
It is easy to prove that the classic knowledge measure formulas above meet the property of non-negative boundedness and symmetry. For the property of order, we have the following Lemma 2.
Lemma 2
meet the property of order KP4I, while
and
don’t meet KP4I.
Proof: According to KP4I,
meet the property of order.
For
, according to
,
, we have:
Therefore, we have
.
Similarly, We also have:
When
,
. Thus we get:
Thus we obtain: For
,
.
Similarly, we also have:
For
,
.
Therefore,
meet the property of order.
According to KP4I,
and
don’t meet KP4I.
For
,
,
. We cannot have
.
Obviously, we cannot get
.
We cannot obtain
too.
Obviously,
cannot be determined. Hence,
does not meet the property KP4I.
For
, we have
and we cannot have
. Hence, We cannot have
and
, Hence,
and
do not meet the property KP4I.
4. Intuitionistic Fuzzy Knowledge Measure Model with Parameter
According to KP4I, knowledge measure
can be considered to be a positive relation to
. In addition, when
is a constant, due to the same difference between membership and non-membership, the greater the minimum value of the degree of membership and non-membership is, the greater the maximum value of the degree of membership and non-membership will be, the higher the degree of known information will be, and hence the larger the knowledge measure value should be under the
same difference between membership and non-membership. Thus, the knowledge measure should be positively correlated to
.
Based on the definition of knowledge measure of IFSs and the analysis above, a model can be achieved:
(14)
is proved to meet all four properties of Definition 6.
Proof: For each
and for each A ∈ IFSs, obviously,
.
(KP1)
.
(KP2)
or
.
(KP3)
.
(KP4I) For
,
Similarly, we also have:
For
,
.
Hence, for each
,
is a knowledge measure of IFSs A.
4.1. Comparison between
and
According to Lemma 2 and the analysis above,
and
meet the property of order, while
and
don’t meet KP4I. Hence, we compare
with
as follows.
(15)
is affected by the difference between membership and non-membership degree with the positive correlation, which is the same as
. Meanwhile, when
, the difference between membership and non-membership degree, is a constant,
is also affected with the positive correlation by the minimum of membership and non-membership degree, while
the negative correlation.
.
From practical significance,
will be more reasonable than
. If
is a constant, then the greater the minimum value of membership and non-membership, the greater the amount of knowledge. For example, if
and
, then we have
, and hence we know that the known extent of A is more than that of B under the same difference between membership and non-membership degree. Thus, it means that
, which is the same as
and different from
.
4.2. Analysis of Parameter p for
Let
.
Obviously,
is a power function of
, and we get
. According to the nature of the power function, we obtain:
1) When
,
is linear function of
.
2) When
,
is a convex function on the defined domain
, which means that if
is close to 0, the amount of information
decreases rapidly; when
approaches 1, the amount of information
increases slowly.
3) Contrary to 2), when
,
is a concave function on the defined domain
, which means that if
is close to 0, the amount of information
decreases slowly; when
approaches 1, the amount of information
increases sharply.
According to the analysis above, in practical applications, people can find suitable information measurement models based on parameter adjustments.
5. Experimental Example and Result Analysis
Example 1. Consider five IFSs,
It is clear that
From Equations (7)-(14), we obtain Table 1. The evaluation index Accuracy
![]()
Table 1. Comparison of experimental results of K (Di), (i = 1, 2, 3, 4, 5).
Note. Each bold data means the wrong prediction result and the corresponding method.
can be defined as follows:
(16)
Results show that for the knowledge measures with the order property, such as KG and Kp, the order of their results is completely correct, while the order of the results for the knowledge measures without the order property, such as KSKB, KBB,
,
, KN, KSK and S(U, V), do not meet the property KP4I. According to Table 1, KG and Kp will be better than the others. Hence, we conclude that KG and Kp are better than the others.
A type of classic intuitionistic fuzzy sets
are used to compare and analyze the difference of results among the proposed
and all those traditional knowledge measure formulas [18] .
Example 2. Let
be an IFS in X. For any positive real number m, De et al. define the IFS
as follows [18]:
.
Obviously, we have
,
,
, and a series of IFSs for contrast experiments can be constructed.
Using the operation above, they defined the concentration and dilation of A as follows:
Concentration:
.
Dilation:
.
Like fuzzy sets,
and
can be treated as “Very (A)” and “More or less (A)”, respectively.
In the next, we consider an IFS A in X = {6, 7, 8, 9, 10} defined in reference [9] [13] [17] as follows:
Taking into account the characteristics of the value of language variables, De et al. define IFS
in X to be “More or Less Large”, “Large”, “Very Large”, “Quite Very Large”, “Very Very Large”. In the same way,
and
can be defined [17] .
From the data above, for each
, we obtain:
According to the definition of knowledge measure of IFSs, obviously we get:
The results are shown in the following Tables 2-4.
Where the evaluation index Accuracy is defined as follows:
(17)
![]()
Table 2. Comparison of experimental results from Ak.
Note. Each bold data means the wrong prediction result and the corresponding method.
![]()
Table 3. Comparison of experimental results from Bk.
Note. Each bold data means the wrong prediction result and the corresponding method.
![]()
Table 4. Comparison of experimental results from Ck.
Note. Each bold data means the wrong prediction result and the corresponding method.
Based on the theoretical derivation,
and
satisfy the property of order KP4I, while
and
do not Satisfy this property. From the comparative analysis of the results in Tables 2-4, we found that the overall order accuracy of
is 89%, and that of
is 93.3%, owning the highest accuracy among all methods. Moreover, From Example 1 - 2, the order of all the results from
and
is exactly the same. And for the order of all the results from
and
, there is only slight differences in Example 2 between them. Hence the overall performance of
is acceptable.
6. Conclusion
On the basis of Szmidt & Kacprzyk’s axiom system, a simple model of knowledge measure with parameters is presented. And we illustrate the validity of the measure tool from the theoretical and empirical evidence. At the same time, this paper also applies the proposed knowledge measure, along with some classical knowledge measure formulas of IFSs, from the theoretical and practical comparison, to verify a conclusion: In most knowledge measures of IFSs, the accuracy of those formulas satisfying the order property will be higher than that of those not satisfying.
Funds
This paper is funded by the National statistical research key projects (No. 2016LZ18), Natural Science Projects (No. 2016A030310105, 2018A030313470) & Soft Science Project (No. 2015A070704051, 2016A030313688) & Quality engineering and teaching reform project (No. 125-XCQ16268) of Guangdong Province, Philosophy and Social Science Project of Guangzhou (No. 2017GZYB45), Team Project Guangdong University of Foreign Studies (No. TD1605), National Undergraduate Training Program for Innovation and Entrepreneurship of China (No. 201511846058, 201711846004).
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.