Penetrative Bénard-Marangoni Convection in a Micropolar Ferrofluid Layer via Internal Heating and Submitted to a Robin Thermal Boundary Conditions ()
1. Introduction
Ferrofluids are colloidal suspensions of magnetic nanoparticles, as suggested by Rosensweig [1] in his monograph, it is pertinent to consider the effect of micro-rotation of the particles in the study. Based on this fact, studies have been undertaken by treating ferrofluids as micropolar fluids and the theory of micropolar fluid proposed by Eringen [2] has been used in investigating the problems. Micropolar fluids have been receiving a great deal of interest and research focus due to their applications like solidification of liquid crystals, the extrusion of polymer fluids, cooling of a metallic plate in a bath colloidal suspension solutions and exotic lubricants. In the uniform magnetic field, the magnetization characteristic depends on particle spin but does not on fluid velocity: Hence micropolar ferrofluid stability studies have become an important field of research these days. Although convective instability problems in a micropolar fluid layer subject to various effects have been studied extensively, the works pertaining to micropolar ferrofluids are in much-to-be desired state. Many researchers (Lebon and Perez [3] , Payne and Straughan [4] , Siddheshwar and Pranesh [5] , Idris et al. [6] , Mahmud et al. [7] , Sharma and Kumar [8] ) have been rigorously investigated the Rayleigh-Bénard situation in Eringen’s micropolar non-magnetic fluids. From all these studies, they mainly found that stationary convection is the preferred mode for heating from below. Zahn and Greer [9] have considered interesting possibilities in a planar micropolar ferromagnetic fluid flow with an AC magnetic field. Abraham [10] has investigated the problem of Rayleigh-Bénard convection in a micropolar ferromagnetic fluid layer permeated by a uniform magnetic field for stress-free boundaries. Thermal instability problem in a rotating micropolar ferrofluid has also been considered by Sunil et al. [11] . Nanjundappa et al. [12] have investigated the onset of ferromagnetic convection in a micropolar ferromagnetic fluid layer heated from below in the presence of a uniform applied vertical magnetic field.
The practical problems cited above require a mechanism to control thermomagnetic convection. One of the mechanisms to control (suppress or augment) convection is by maintaining a non-uniform temperature gradient across the layer of ferrofluid. Such a temperature gradient may arise due to 1) uniform distribution of heat sources 2) transient heating or cooling at a boundary, 3) temperature modulation at the boundaries and so on. Works have been carried out in this direction but it is still in much-to-be desired state. Rudraiah and Sekhar [13] have investigated convection in a ferrofluid layer in the presence of uniform internal heat source. The effect of non-uniform basic temperature gradients on the onset of ferroconvection has been analyzed (Shivakumara et al. [14] , and Shivakumara and Nanjundappa [15] [16] ). Singh and Bajaj [17] have studied thermal convection of ferrofluids with boundary temperatures modulated sinusoidally about some reference value. Nanjundappa et al. [18] have studied the effect of internal heat generation on the criterion for the onset of convection in a horizontal ferrofluid saturated porous layer Nanjundappa et al. [19] have explored a model for penetrative ferroconvection via internal heat generation in a ferrofluid saturated porous layer. Nanjundappa et al. [20] have investigated the onset of penetrative Bénard-Marangoni convection in a horizontal ferromagnetic fluid layer in the presence of a uniform vertical magnetic field via an internal heating model. Ram and Kumar [21] has carried out to examine the effects of temperature dependent variable viscosity on the three dimensional steady axi-symmetric Ferrohydrodynamic (FHD) boundary layer flow of an incompressible electrically non conducting magnetic fluid in the presence of a rotating disk. Ram and Kumar [22] have analyzed the analysis of three dimensional rotationally symmetric boundary layer flow of field dependent viscous ferrofluid saturating porous medium. Ram et al. [23] have been made to describe the effects of geothermal viscosity with viscous dissipation on the three dimensional time dependent boundary layer flow of magnetic nanofluids due to a stretchable rotating plate in the presence of a porous medium. Ram et al. [24] have investigated numerically on the convective heat transfer behaviour of time-dependent three-dimensional boundary layer flow of nano-suspension over a radially stretchable surface. Kumar et al. [25] have studied the Bodewadt flow of a magnetic nanofluid in the presence of geothermal viscosity. Very recently, Ram et al. [26] have studied the rheological effects due to oscillating field on time dependent boundary layer flow of magnetic nanofluid over a rotating disk.
The purpose of this paper is to study the penetrative Bénard-Marangoni convection in a micropolar ferromagnetic fluid layer via internal heat generation. Such a study helps in understanding control of convection due to a non-uniform temperature gradient arising due to an internal heat source, which is important in the applications of ferrofluid technology. The linear stability problem is solved numerically using the Galerkin method, and the results are presented graphically. Moreover, the stability of the system when heated from below and also in the absence of thermal buoyancy is discussed in detail.
2. Mathematical Formulation
We consider an initially quiescent horizontal incompressible micropolar ferrofluid layer of characteristic thickness d in the presence of an applied uniform magnetic field H0 in the vertical direction with the angular momentum
. Let
and
be the temperatures of the lower and upper rigid boundaries, respectively with
being the temperature difference. A uniformly distributed overall internal heat source is present within the micropolar ferrofluid layer. The Cartesian co-ordinate system
is used with the origin at the bottom of the layer and z-axis is directed vertically upward. Gravity acts in the negative z-direction,
where
is the unit vector in the z-direction.
The upper free boundary is assumed to be flat and subjected to linearly temperature dependent surface tension σ is
,
is the rate of thermal surface tension.
The governing equations for the flow of an incompressible micropolar ferromagnetic fluid are:
(1)
(2)
(3)
(4)
(5)
,
or
(6)
(7)
(8)
(9)
The basic state is assumed to be quiescent and is given by
(10)
Using Equation (10) in Equation (2) and (4) respectively yield
(11)
(12)
Solving Equation (12) subject to the boundary conditions
at
and
at
, we obtain
(13)
Substituting Equation (6) after using Equations (9) and (13), the basic state magnetic field intensity
and magnetization
are found to be (see Finlayson [4] )
(14)
(15)
where
.
Using Equations (13) and (14) in Equation (11) and integrating, we obtain
(16)
The pressure distribution is of no consequence here as we are eliminating the same. It may be noted that
,
and
are distributed parabolically with the porous layer height due to the presence of internal heat generation. However, when
(i.e., in the absence of internal heat generation), the basic state temperature distribution is linear in z. Thus the presence of internal heat generation plays a significant role on the stability of the system.
To study the stability of the system, we perturb all the variables in the form
(17)
where
and
are the perturbed quantities and are assumed to be very small. Substituting Equation (17) into Equation (6) and using Equations (8) and (9) and assuming
and
as propounded by Finlayson [4] , we obtain (after dropping primes)
(18)
where,
and
are the
components of the magnetic field and magnetization respectively. Thus the analysis is restricted to physical situation in which the magnetization induced by the variations in temperature gradient and internal heating is small compared that induced by external magnetic field.
Substituting Equation (17) into Equation (2), linearizing, eliminating the pressure term by operating curl twice and using Equations (18) the z-component of the resulting equation can be obtained as (after dropping the primes)
(19)
Substituting Equation (17) into Equation (3) we obtain (after dropping primes)
(20)
As before, substituting Equation (17) into Equation (4) and linearizing, we obtain (after dropping primes)
(21)
where
.
Finally Equation (6), after using Equation (17) and (18), yield (after dropping primes)
(22)
Since the principle of exchange of stability is valid, the normal mode expansion of the dependent variables takes the form
(23)
On non-dimensionalizing the variables by setting
(24)
Equation (23) is substituted into Equations (19)-(22) and then Equation (24) is used to obtain the stability equations in the following form
(25)
(26)
(27)
(28)
The typical value of M2 for magnetic fluids with different carrier liquids turns out to be of the order of 10−6 and hence its effect is neglected when compared to unity.
The above equations are to be solved subject to the rigid-paramagnetic boundary conditions:
(29)
3. Numerical Solution
Equations (25)-(28) together with boundary conditions (29) constitute an eigenvalue problem with thermal Rayleigh number Rt being an eigenvalue. Accordingly,
and
are written as
(30)
where
and
are the unknown constants to be determined. The basis functions
,
,
and
are generally chosen such that they satisfy the corresponding boundary conditions but not the differential equations. Substituting Equation (30) into Equations (25)-(28) and multiplying the resulting momentum Equation (25) by
, angular momentum Equation (26) by
, energy Equation (27) by
and magnetic potential Equation (28) by
, performing integration by parts with respect to z between
and
and using the boundary conditions (29) we obtain the following system of linear homogeneous algebraic equations:
(31)
(32)
(33)
(34)
where the co-efficient
-
involve the inner product of the basis functions and are given by
where the inner product is defined as
. The set of
homogeneous algebraic equations can have non-trivial solutions if and only if
(35)
The eigenvalue has to be extracted from the above characteristic equation. In Galerkin method, we choose the weighting function as the trial functions, thus:
(36)
The velocity (
), temperature (
), vorticity (
) and magnetic potential (
) trail functions satisfy all the boundary condition while the temperature (
) does not satisfy the boundary condition
at
. Therefore, following, the boundary residual technique is used for these functions. The velocity, vorticity and the magnetic equations are made orthogonal to each of the corresponding trail functions. For the temperature trial the boundary residuals are added and their combined inner product is set to zero to obtain
. Besides, the residual from this condition is included as residual from the differential Equation (36) leads to a relation involving in the form
.
The critical values of Rt (i.e., Rc) or Rm (i.e., Rmc) or Ma (i.e., Mac) is determined numerically with respect to a for different values of Ns, M1, M3, N1, N3 and N5.
4. Result and Discussion
The classical linear stability analysis has been carried out to investigate the effect of internal heat source strength on the onset of Bénard-Marangoni ferroconvection in a horizontal micropolar ferrofluid layer heated from below in the presence of a transverse uniform vertical magnetic field. The both the boundaries is considered to be rigid-ferromagnetic. The critical thermal Rayleigh number (Rtc), critical magnetic Rayleigh number (Rmc) and critical Marangoni number (Mac) and the corresponding critical wave number (ac) are used to characterize the stability of the system. The critical stability parameters computed numerically by Galerkin technique as explained above, are found to converge by considering nine terms in the Galerkin expansion.
To validate the solution computed numerically for various values of Rt and Bi in the absence of micropolar effects and internal heat source strength (i.e.
) are compared in Table 1 with the previously published results of Davis [27] . In addition, the present method are compared with the previously published results of Char and Chiang [28] when
and
(classical Rayleigh-Bénard problem) for various values of Ns (see Table 2). From the Tables, it is observed that our results are identical
![]()
Table 1. Comparison of Mac for diff values of Rt and Bi in the absence of micropolar ferrofluid.
![]()
Table 2. Comparison of Rtc for diff values of Ns and Bi in the absence of micropolar ferrofluid.
with those obtained by Davis [27] as well as Char and Chiang [28] using different approaches.
The presence of internal heating makes the basic temperature, magnetic field and magnetization distributions to deviate from linear to parabolic with respect to micropolar ferrofluid layer height which in turn have significant influence on the stability of the system. To assess the impact of internal heat source strength Ns on the criterion for the onset of ferroconvection, the distributions of dimensionless basic temperature,
, magnetic field intensity,
and magnetization,
are exhibited graphically in Figure 1 for various values of Ns. From the figure it is observed that increase in Ns amounts to large deviations in these distributions which in turn enhance the disturbances in the horizontal
![]()
Figure 1. Basic state temperature, magnetic intensity and magnetization distributions for different Ns.
porous layer and thus reinforce instability on the system.
Figures 2-4 depict the critical Mac at the onset of ferroconvection as the function of “a”. It is noted that, as “a” decreases the Marangoni number decreases, attains a minimum at some critical wave number, and increases again. The curves reported in figures have the shape is upward concave to that of Bénard-Marangoni-ferroconvection. For increasing Rm, Ns, N3, Rt, and decreasing N1 is shifted to the neutral curves are slanted towards the higher wave number region.
Figure 5 represents the variation of critical Marangoni number Mac as a function of N1 for different values of Rm and N5 for
,
and
. It is seen that Mac decreases with an increase in Rm and hence its effect is to hasten the onset of ferroconvection due to an increase in the destabilizing magnetic force and the curve for
corresponds to non-magnetic micropolar fluid case. In other words, heat is transported more efficiently in magnetic fluids as compared to ordinary micropolar fluids. Also observed that Mac increases with increasing N1. This is because, as N1 increases the concentration of microelements also increases and as a result a greater part of the energy of the system is consumed by these elements in developing gravitational velocities in the fluid which ultimately leads to delay in the onset of ferromagnetic convection. Moreover, the system is found to be more stable if the micropolar heat conduction of the parameter with
as compared to the case of
.
In Figure 6 Mac is plotted as a function of N1 for different values of spin diffusion (couple stress) parameter N3 and Rm when
,
and
. Here, it is observed that Mac curves for different N3 coalesce when
. The impact of N3 on the stability characteristics of the system is noticeable clearly with increasing N1 and then it is seen that the critical Marangoni
![]()
Figure 2. Neutral curves for different values of
and
with
.
![]()
Figure 3. Neutral curves for different values of
and
for
and
.
number decreases with increasing N3 indicating the spin diffusion (couple stress) parameter N3 has a destabilizing effect on the system. This may be attributed to the fact that as N3 increases, the couple stress of the fluid increases, which leads to a decrease in micro-rotation and hence the system becomes more unstable.
Figure 7 shows the variation of critical Marangoni number Mac and as a function of N1 for various values of dimensionless internal heat source strength Ns when
,
and
. Figure 7 clearly indicates that Mac decreases monotonically with Ns indicating the influence of increasing internal heating is to decrease the value of Mac and thus destabilize the system. This is because increasing Ns amounts to increase in energy supply to the system.
![]()
Figure 4. Neutral curves for different values of
and
with
and
.
![]()
Figure 5. Variation of
verses
for different
for
.
The complementary effects of both buoyancy and magnetic forces are made clear in Figure 8 by displaying the locus of Mac and magnetic Rayleigh number Rmc for various values of Bi and N5 when
, 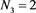 and
and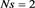 . We note that Mac is inversely proportional to Rmc due to the destabilizing magnetic force. From the figure it is evident that, increasing in Bi is to increase Mac and Rmc and thus its effect is to delay the onset of magnetic Bénard-Marangoni ferroconvection. This may be attributes to fact that with increasing Bi, the thermal disturbances can be easily dissipate in to the ambient surrounding due to a better convective heat transfer co-efficient at the top surface and hence higher
. We note that Mac is inversely proportional to Rmc due to the destabilizing magnetic force. From the figure it is evident that, increasing in Bi is to increase Mac and Rmc and thus its effect is to delay the onset of magnetic Bénard-Marangoni ferroconvection. This may be attributes to fact that with increasing Bi, the thermal disturbances can be easily dissipate in to the ambient surrounding due to a better convective heat transfer co-efficient at the top surface and hence higher
heating is required at make the system unstable. It is also evident that micropolar ferrofluid saturated porous layer in the presence of vertical magnetic field becomes more stable with increasing in Bi.
The measure of non-linearity of fluid magnetization M3, on the onset of ferroconvection is depicted in Figure 9. The curves of Mac versus Rmc shown in Figure 9 for various values of M3 when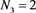 ,
,  ,
, ![]() and
and ![]() demonstrate that increasing M3 has a destabilizing effect on the system. Nevertheless, the destabilization due to increase in M3 is only marginal. This may be
demonstrate that increasing M3 has a destabilizing effect on the system. Nevertheless, the destabilization due to increase in M3 is only marginal. This may be
attributed to the fact that the application of magnetic field makes the ferrofluid to acquire larger magnetization which in turn interacts with the imposed magnetic field and releases more energy to drive the flow faster. Hence, the system becomes unstable with a smaller temperature gradient as the value of M3 increases. Alternatively, a higher value of M3 would arise either due to a larger pyromagnetic coefficient or larger temperature gradient. Both these factors are conducive for generating a larger gradient in the Kelvin body force field, possibly promoting the instability.
5. Conclusions
The effect of internal heating and heat transfer coefficient on the onset of Bénard-Maranagoni-convection in a micropolar ferrofluid layer has been made theoretically. The solution of this problem is obtained numerically using Galerkin-type of weighted residual technique by developing computer codes for MATTHEMAICA-11 software. Tabular and graphical method of appearance of the computed results illustrates the details in this paper and their dependence on the physical parameters involved in the problem. The significant findings of this analysis are:
1) The system becomes more unstable with an increase in magnetic Rayleigh number Rm, nonlinearity of fluid magnetization parameter M3, internal heat source strength Ns and spin diffusion (couple stress) parameter N3.
2) The effect of increasing the value of coupling parameter N1, micropolar heat conduction parameter N5, Biot number Bi and is to delay the onset of ferromagnetic convection.
3) The effect of increasing Rm and Ns as well as decrease in N1, M3, N3 and N5 is to increase the critical wave number ac and hence there is to reduce the convection cells.
4) The magnetic and buoyancy forces are complementary with each other and the system is more stabilizing when the magnetic forces alone are present.
Acknowledgements
The authors gratefully acknowledged the financial support received in the form of a “Research Fund for Talented Teacher” scheme from Vision Group of Science & Technology, Government of Karnataka, Bengaluru (No. KSTEPS/ VGST/06/2015-16).
Nomenclature
![]() : Velocity of the fluid
: Velocity of the fluid
![]() : Pressure
: Pressure
![]() : Moment of inertia
: Moment of inertia
![]() : Thermal conductivity
: Thermal conductivity
![]() : Temperature
: Temperature
![]() : Specific heat at constant volume and magnetic field
: Specific heat at constant volume and magnetic field
![]() : Magnetic induction field
: Magnetic induction field
![]() : Magnetic field
: Magnetic field
![]() : Constant magnetic field
: Constant magnetic field
![]() : Pyromagnetic co-efficient
: Pyromagnetic co-efficient
![]() : Magnetization
: Magnetization
![]() : Constant mean value of magnetization
: Constant mean value of magnetization
![]() : Overall uniformly distributed effective volumetric internal heat generation
: Overall uniformly distributed effective volumetric internal heat generation
![]()
![]()
![]() : Differential operator
: Differential operator
![]() : Overall horizontal wave number
: Overall horizontal wave number
![]() : Gravity thermal Rayleigh number
: Gravity thermal Rayleigh number
![]() : Magnetic number
: Magnetic number
![]() : Magnetic parameter
: Magnetic parameter
![]() : Non-linearity of magnetization
: Non-linearity of magnetization
![]() : Magnetic Rayleigh number
: Magnetic Rayleigh number
![]() : Coupling parameter:
: Coupling parameter:
![]() : Spin diffusion parameter
: Spin diffusion parameter
![]() : Micropolar heat conduction parameter
: Micropolar heat conduction parameter
![]() : Dimensionless heat source strength
: Dimensionless heat source strength
![]() : Prandtl number
: Prandtl number
Greek Symbols
![]() : Density
: Density
![]() : Shear kinematic viscosity co-efficient
: Shear kinematic viscosity co-efficient
![]() : Vortex (rotational) viscosity
: Vortex (rotational) viscosity
![]() : Angular velocity of colloidal particles along z-axis
: Angular velocity of colloidal particles along z-axis
![]() : Reference density
: Reference density
![]() : Free space magnetic permeability
: Free space magnetic permeability
![]() : Shear spin viscosity co-efficient
: Shear spin viscosity co-efficient
![]() : Thermal expansion co-efficient
: Thermal expansion co-efficient
![]() : Micropolar heat conduction coefficient
: Micropolar heat conduction coefficient
![]() : Magnetic susceptibility
: Magnetic susceptibility
![]() : Magnetic potential
: Magnetic potential
![]() : Laplacian operator
: Laplacian operator
![]() : Convective derivative
: Convective derivative
![]() (
(![]() ): Temperature gradient
): Temperature gradient