Buffer standards for the physiological pH of the zwitterionic buffer 3-[N-tris(hydroxymethyl)methylamino]-2-hydroxypropanesulfonic Acid (TAPSO) From (278.15 to 328.15) K ()
1. INTRODUCTION
Good and his associates [1,2] have suggested several useful zwitterionic amino acid buffer solutions used in measuring the pH of blood and having the pH constrained so it closely reflects that of the physiological range (pH =7 - 9). Very recently, the authors have reported the pH values of 3-(N-morpholino)-2-hydroxypropanesulfonic acid (MOPSO) [3] from (278.15 to 328.15) K, including 310.15 K. The zwitterionic buffer 3-[N,N-bis(2-hydroxymethyl)amino]-2-hydroxypropanesulfonic acid (DIPSO)[4] is also recommended for physiological use at (278.15 to 328.15) K. Regarding the current experiment the goal of the authors is to provide staunch pH values for the ampholyte 3-[N-tris(hydroxymethyl)-methylamino]-2-hydroxypropanesulfonic acid (TAPSO) depicted by the following structure:
This zwitterionic buffer, among others suggested by Bates and coworkers [5,10], may be used as biological buffers for biological media. The currently used NBS certified physiological phosphate primary standard buffer has recorded pH values of 7.415 and 7.395 at (298.15 and 310.15) K, respectively [5]. This phosphate buffer is comprised of KH2PO4 (0.008695 mol·kg–1) and Na2HPO4 (0.03043 mol·kg–1). Though it has been accepted by the NBS, problems still occur when using this particular phosphate buffer.
Some of the disadvantages concerning the phosphate buffer are: 1) phosphates precipitate some polyvalent cations in the blood, such as the constituents Mg2+ and Ca2+; 2) the phosphate may also inhibit or unnecessarily activate enzymatic processes such as some metabolic cycles; and 3) the phosphate buffer’s temperature coefficient (–0.0028 pH unit·K–1) does not accurately approximate that of whole blood (–0.015 pH unit·K–1) [6]. The zwitterionic buffer compound TAPSO is not expected to yield such adverse effects, but the potential for complex formation with cations such as Mg2+ and Ca2+ does still exist. The likeliness of this occurring has been minimized with a high NaCl: buffer concentration ratio for an isotonic saline solution of I = 0.16 mol·kg–1.
Good and coworkers established a group of hydrogennion buffers suitable for use within the physiological pH range [1,2]. They also cited published works from other

Figure 1. 3-[N-tris(hydroxymethyl)methylamino]- 2-hydroxypropanesulfonic acid (TAPSO).
researchers for structurally related zwitterionic buffer compounds and their substituents for comparison of their pH and pK2 values. Wu and associates [7] have published pH and pK2 values for N-(2-hydroxyethyl)piperazine-N- 2-ethanesulfonic acid (HEPES), another zwitterionic buffer. Wu et al. [8] have also studied MOPSO using two point pH calibration measurements. Roy et al.[9] studied pK2 and pH values of 3-(N-morpholino)propanesulfonic acid (MOPS) and reported the results in the temperature range of (278.15 to 328.15) K, including 310.15 K. The previously mentioned buffer solutions have yielded a pH similar to common biological media.
The following compositions were examined with solutions (a) to (e) lacking the NaCl and solutions (f) to (j) containing NaCl resulting in an ionic strength of I = 0.16 mol·kg–1:
(a) TAPSO (0.04 mol·kg–1) + NaTAPSO (0.02 mol·kg–1)
(b) TAPSO (0.06 mol·kg–1) + NaTAPSO (0.03 mol·kg–1)
(c) TAPSO (0.05 mol·kg–1) + NaTAPSO (0.05 mol·kg–1)
(d) TAPSO (0.06 mol·kg–1) + NaTAPSO (0.06 mol·kg–1)
(e) TAPSO (0.08 mol·kg–1) + NaTAPSO (0.08 mol·kg–1)
(f) TAPSO (0.02 mol·kg–1) + NaTAPSO (0.04 mol·kg–1) + NaCl (0.12 mol·kg–1)
(g) TAPSO (0.03 mol·kg–1) + NaTAPSO (0.06 mol·kg–1) + NaCl (0.10 mol·kg–1)
(h) TAPSO (0.04 mol·kg–1) + NaTAPSO (0.02 mol·kg–1) + NaCl (0.14 mol·kg–1)
(i) TAPSO (0.06 mol·kg–1) + NaTAPSO (0.03 mol·kg–1) + NaCl (0.13 mol·kg–1)
(j) TAPSO (0.04 mol·kg–1) + NaTAPSO (0.04 mol·kg–1) + NaCl (0.12 mol·kg–1)
The detailed procedure for preparation of the aforementioned TAPSO buffer solutions is described in the Experimental Section below.
2. EXPERIMENTAL
TAPSO was obtained from Research Organics (Cleveland, Ohio). Further crystallization was used for purification. This technique and the assay have been previously reported [8]. It was concluded from the assay that the TAPSO used was 99.99% pure. Buffer solutions (a) to (j) were prepared by massing the TAPSO buffer, ACS reagent grade NaCl, a standard NaOH solution (which allowed the NaTAPSO to be prepared), and finally carefully calculated amounts of CO2-free doubly distilled water. Buoyancy corrections were applied to all masses used during the preparation of the solutions.
In previous publications, the cell design and preparation procedures for the chloroplatinic acid, hydrogen electrodes, purification using hydrogen gas, silver-silver chloride electrodes (of the thermal electrolytic type), and solution preparation have been described [9,12] Details about the equipment (including model numbers) and experimental techniques have also been previously reported [12].
3. METHODS AND RESULTS
The cell voltage values for the paH calculations are given in Tables 1 and 2 for cell A. Cell A contains five solutions lacking their Cl– component and five solutions with Cl– to give them an ionic strength of I = 0.16 mol·kg–1. The cell voltage values have been corrected to a hydrogen pressure of 101.325 kPa. At (298.15) K, cell voltage values are averaged from readings taken once at each portion of the reading (the beginning, middle, and end). Duplicate cells gave readings of ±0.04 mV on average in the temperature range under study.
3.1. pH of the TAPSO Buffer
The Bates et al. [10,11,16-18] method has been used to evaluate the conventional standard pH values for solutions (a) to (j) described in the Introduction. For accurate calculations of the ten buffer solutions, the following cell A was used for the collection of cell potential data:
Pt(s), H2(g), 101.325 kPa | TAPSO (m1) +
NaTAPSO (m2) + NaCl (m3) | AgCl(s), Ag(s) (A)
where m1, m2 and m3 denote the molalities of the respective species at 1 atm = 101.325 kPa in SI units. Cell A is known as the Harned-type cell.
3.2. Evaluation of Liquid Junction Potential
Cell B, the flowing junction cell, was used to evaluate the liquid junction potential at the contact point between the buffer solution and the heavier, saturated KCl solution shown with a double vertical line as follows:
Pt(s), H2(g), 101.325 kPa | TAPSO (m1) + NaTAPSO
(m2) + NaCl (m3) || KCl(satd), Hg2Cl2(s), Hg(l) (B)
where the abbreviations “s,” “l,” and “g” indicate the solid, liquid, and gaseous states, respectively. In routine laboratory measurements, a glass electrode commonly replaces the hydrogen electrode. For cell B, the values of the standard electrode potential, denoted as , of the saturated calomel electrode were recorded as –0.2415 V
, of the saturated calomel electrode were recorded as –0.2415 V

Table 1. Cell potential of cell A (in volts): Pt(s); H2(g), 101.325 kPa | TAPSO (m1), NaTAPSO (m2), NaCl (m3) | AgCl(s), Ag(s).

Table 2. Cell potential of cell A (in volts): Pt(s); H2(g), 101.325 kPa | TAPSO (m1), NaTAPSO (m2), NaCl (m3) | AgCl(s), Ag(s).
and –0.2335 V at (298.15 and 310.15) K, respectively. These values are periodically confirmed through experimentation.
3.3. Application in Physiological Media
For cell C, the phosphate salts were NBS standard reference materials whose compositions were mentioned in the Introduction. Its solutions are recommended for pH measurements in physiological media. Cell C’s cell diagram is as follows:
Pt(s), H2(g), 101.325 kPa | KH2PO4 + Na2HPO4 ||
KCl(satd), Hg2Cl2(s), Hg(l) (C)
3.4. Application of Liquid Junction Corrections
The  values of the saturated calomel electrode were recorded as –0.2415 and –0.2335 at (298.15 and 310.15) K, respectively [8,9]. The Ej values were also obtained by use of the flowing junction cell [9]. The Ej values of the standard buffer solution, as well as others in cell B, were calculated using the following equation:
values of the saturated calomel electrode were recorded as –0.2415 and –0.2335 at (298.15 and 310.15) K, respectively [8,9]. The Ej values were also obtained by use of the flowing junction cell [9]. The Ej values of the standard buffer solution, as well as others in cell B, were calculated using the following equation:
Ej = E +  – kpH (1)
– kpH (1)
where k = 0.059156 and pH = 7.415 at (298.15) K and k = 0.061538 and pH = 7.395 at (310.15) K. The pH inputs are that of the standard phosphate buffer solution. The operational definition of pH, denoted as pH(x), can be calculated by use of the subsequent equation:
 (2)
(2)
where the subscript “x” refers to the unknown buffer (in this case, a solution of TAPSO + NaTAPSO), “s” is the NBS standard buffer solution of a known pH, and δEj = Ej(s) – Ej(x). The dEj value is of interest rather than the actual Ej value in mV.
To calculate the paH values for the buffer solutions under investigation, the acidity function was calculated, denoted as p(aHgCl), in the temperature range of (278.15 to 328.15) K. These calculations were made using the cell voltage (E) values listed in Tables 1 and 2, the molality of the chloride ion, and the standard electrode potential of the silver-silver chloride electrode (E˚). The tool used to calculate p(aHgCl), the Nernst equation [11, 12], is shown below:
 (3)
(3)
where “k” is the Nernst slope.
3.5. Plotting of Results
When plotting p(aHgCl) against the molality of the chloride ion, linear regression analysis is used to determine the y-intercept to give a p(aHgCl)˚ value at mCl = 0. These p(aHgCl)˚ values for the five chloride-free buffer solutions are listed in Table 3. The mean deviation from this linear regression technique was approximately 0.002 from the lines generated. The p(aHgCl) values for the buffer solutions containing Cl– are listed in Table 4 from (278.15 to 328.15) K.
3.6. Calculation of pH Results
Conventional paH values for solutions without a liquid junction and a chloride ion were determined using the following equation:
 (4)
(4)
where the single-ion activity coefficient,  , cannot be experimentally measured. A previous publication describes the method used for obtaining this figure [9]. The pH values obtained from the liquid junction cell are indicated by pH whereas the “conventional” pH, calculated from Eq.5, is denoted as paH. The “pH convention,” commonly known as the Bates-Guggenheim convention [17] is expressed by the use of the successive equation:
, cannot be experimentally measured. A previous publication describes the method used for obtaining this figure [9]. The pH values obtained from the liquid junction cell are indicated by pH whereas the “conventional” pH, calculated from Eq.5, is denoted as paH. The “pH convention,” commonly known as the Bates-Guggenheim convention [17] is expressed by the use of the successive equation:
 (5)
(5)
The International Union of Pure and Applied Chemistry has recommended this convention. Eq.5 is assumed to be true for concentrations I < 0.1 mol·kg–1. For I > 0.1 mol·kg–1, there is no widely accepted convention. A more logical choice for solutions with I > 0.01 mol·kg–1 may need to include a linear-dependent “CI” term from Eq.6 with the ion size parameter as a function of temperature.
Due to this need for alteration, a pH convention [7,9] based on an extended version of the Debye-Hückel equation [7] has been selected as a more logical approach to calculate  when (0.1 < I < 1.0) mol·kg–1 for all of the buffer solutions containing Cl–. This equation is shown below:
when (0.1 < I < 1.0) mol·kg–1 for all of the buffer solutions containing Cl–. This equation is shown below:
 (6)
(6)
where “I” is the ionic strength of the buffer solution, “A” and “B” are slope parameters known as the DebyeHückel constants, and “C” is an adjustable parameter whose explanation will follow shortly. Ba˚ was assumed to be 1.38 kg1/2·mol–1/2 for all the experimental temperatures. This corresponded to an ion size parameter, a˚, of 4.2 Å [7,9]. The empirical equation that follows is used for the calculation of the adjustable parameter “C” and was obtained from a curve-fitting method [7,9].
 (7)
(7)
where C298.15 = 0.032 kg·mol–1 at (298.15) K [7] and T is the absolute temperature in Kelvin.
The paH values listed in Table 5 for the five TAPSO buffer solutions without the presence of Cl– were calculated using the following equations with their respective solution denotations:
(a) (8)
(8)
(b) (9)
(9)
(c) (10)
(10)
(d) (11)
(11)
(e) (12)
(12)
for the temperature range of (278.15 to 328.15) K. The standard deviations of regression for the paH of the chloride-free buffer solutions are obtained from lines of best

Table 3. p(aHγCl)° of (TAPSO + NaTAPSO) buffer solutions from 278.15 K to 328.15 K obtained by extrapolation for chloride-free solutions.

Table 4. p(aHγCl) of (TAPSO + NaTAPSO) buffer solutions from 278.15 K to 328.15 K, computed using Eq.4a.

Table 5. paH of (TAPSO + NaTAPSO) buffer solutions from 278.15 K to 328.15 K, computed using Eqs.4-7a.
fit using Eqs.3-7. These standard deviations are 0.0009, 0.0014, 0.0016, 0.0012 and 0.0012, respectively.
For the five buffer solutions containing Cl–, with an isotonic saline media ionic strength of I = 0.16 mol·kg–1, the paH values were also calculated using Eqs.3-7. The acidity function data from Table 4 was also used to generate the paH data residing in Table 6. These values of paH are expressed by use of the following equations:
(a) (13)
(13)
(b)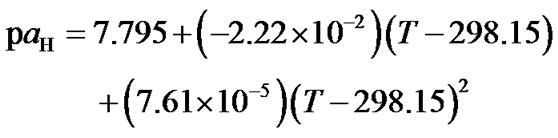 (14)
(14)
(c)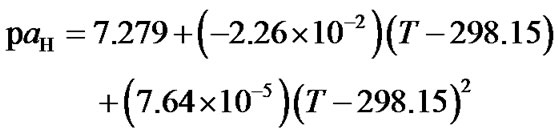 (15)
(15)
(d) (16)
(16)
(e)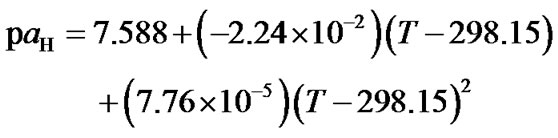 (17)
(17)
The observed standard deviations of regression from Eqs.13-17 are 0.0012, 0.0019, 0.0019, 0.0011 and 0.0010, respectively.
4. DISCUSSION
The operational pH values at (298.15 and 310.15) K were evaluated from cells with a liquid junction (cells B and C) using the flowing junction cell [7,9]. The cell voltage values of cells B and C at (298.15 and 310.15) K are given in Table 7. The values of Ej listed in Table 8 were obtained using Eq.1. The widely used equation for the calculation of  is based on the Bates-Guggenheim convention [3,6,7,10] and is valid for concentrations of I < 0.1 mol·kg–1. The total standard uncertainty for the paH values was accounted for by combining various known sources of error: 1) extrapolation of the p(aHgCl)˚ plot for Cl– free solutions (error is < ±0.002 pH unit); 2) assumption for the calculation of
is based on the Bates-Guggenheim convention [3,6,7,10] and is valid for concentrations of I < 0.1 mol·kg–1. The total standard uncertainty for the paH values was accounted for by combining various known sources of error: 1) extrapolation of the p(aHgCl)˚ plot for Cl– free solutions (error is < ±0.002 pH unit); 2) assumption for the calculation of  using Eq.6 (error of ±0.004 pH unit); and 3) the error in the experimental measurement from the multimeter (an error of ±0.02 mV). This yields an overall error of ±0.012 pH and ±0.006 pH unit for buffer solutions with and without the presence of Cl–, respectively. Errors in values of Ej are irrelevant to the values of paH determined from cell A without liquid junction; however, Ej of Eq.2 does affect the operational paH values listed in Table 9 at (298.15 and 310.15) K.
using Eq.6 (error of ±0.004 pH unit); and 3) the error in the experimental measurement from the multimeter (an error of ±0.02 mV). This yields an overall error of ±0.012 pH and ±0.006 pH unit for buffer solutions with and without the presence of Cl–, respectively. Errors in values of Ej are irrelevant to the values of paH determined from cell A without liquid junction; however, Ej of Eq.2 does affect the operational paH values listed in Table 9 at (298.15 and 310.15) K.
5. CONCLUSIONS
The four buffer solutions listed in Tables 7-9 are recommended as useful secondary pH standards for calibrating electrodes for pH measuring assembly in the physiological range. The consistency of the three sets of experiments listed in Table 9 leads credibility to the pH values of these TAPSO buffer solutions as primary standards for physiological use.
6. ACKNOWLEDGEMENTS
The authors are grateful for the funding from the National Institutes

Table 6. paH of (TAPSO + NaTAPSO) buffer solutions from 278.15 to 328.15 K, computed using Eqs.4-7a.

Table 7. Cell voltage of cell B for TAPSO buffer.

Table 8. Values of the liquid junction potentials for TAPSO buffer at (298.15 and 310.15) K.

Table 9. Values of pH at (298.15 and 310.15) K for TAPSO buffer solutions.
of Health (AREA), under the grant 2-R15 GM 066866-03 and the diversity supplemental grant 3-R15 GM 066866-03 S1. The authors would also like to thank Josie Yost and Rhode Doriscar for their dedication and hard work. The content of this paper is the sole responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or the National Institutes of General Medical Sciences.