1. Introduction
The M-BCJR [1] is a low complexity version of the leader MAP-BCJR (Maximum A Posteriori) algorithm [2]. It consists to use only M best metrics in trellis. Others states are not evaluated next step, so the complexity is reduced. The M-BCJR finds its applications in turbo equalisation [3] where more variants are proposed [4-6]. It can reduce trellis of detectors to M states, but when M decreases, performances will be degraded [7]. Note that for turbo equalisation, some designs use very low complexities (two “2” states only) without M-BCJR strategy [8].
For turbo decoding [9], there are no variants of M-BCJR. The performances are not acceptable. The reduction of the recursions to a constant M computation paths through the trellis was not successful [1]. The imperfection of the M-BCJR is in the fact that it presents degraded performances when the complexity is reduced. Other strategy is better than M-BCJR such as T-BCJR algorithm [1] where the states that have values less than threshold T are forced to zero but in this case, number of state is varying.
In order to enhance the performances of M-BCJR algorithm, an optimal version is proposed in this paper. it offers same performances of full MAP-BCJR turbo decoding with the same complexity of the M-BCJR algorithm.
The rest of the paper is organized as follows: In Section 2 and 3, we present the behavior of the M-BCJR algorithm and characterization of its error instants. In Section 4, we explain our idea for improvement this algorithm and we detail our new algorithm Z-MAP. Finally, in Section 5 we present the results of our simulations and conclude with the evaluation of our improvements.
2. M-BCJR Behavior
Let us show quickly the principle of M-BCJR. It simply consists to keep the M significant values of alpha 
in the forward (beta 
in the backward). The other states are declared dead and set to 0. This implies a reduction of: calculated states (alpha, beta forced to zero), outgoing branches of each state (thus gamma, also forced to zero) because [2]:
(1)
and
(2)
Our observations of M-BCJR algorithm show that its weakness is error amplification. The nature of M-BCJR algorithm causes bad estimations of alpha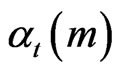 
due to zero forcing of some states. This causes a frame of errors. At erroneous moments, we observe one or more concurrents with the most probable state in trellis. The unique way to correct this is increasing states number. We call this mechanism Z-MAP algorithm. Z designs go, stop in error instance, back and increase states number. This is similar to “Z” letter.
3. Error Moments
In M-BCJR decoding, we observe that the correct instants are characterized by an impulse with high alpha value for the probable state (Figure 1). Others alphas have very little levels (probabilities) due to more zeros at previous instants. The presence of error is generally characterized by a presence of one or more competitors in alpha values (Figure 2). This phenomena can be used as an easy criterion to locate error possibility.
For example, let us take a trellis with “4” states (Figure 3) of an encoder which has a strength length equal to “3”. We establish a relation between instant “n” and the
Figure 1. The most probable state in correct instant.
Figure 2. Presence of concurrent in error instant.
past. Let us take this past “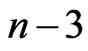
”. In this case, alpha of state “0” is given by :
(3)
We suppose that at “
”, 
is forced to zero with M-BCJR mechanism. This event changes the four alphas
, 
, 
and 
with different quantities. This phenomena generates a competitor in M-BCJR decoding.
Figure 4 shows an example of the difference 
between real alpha values of full MAP-BCJR and those of M-BCJR algorithm for trellis of Figure 3. We use SNR (Eb/N0) equals to 0 dB. The 
is forced to zero. It affects next near 15 alphas for all states with different amplitudes. Theses fluctuations are the reason of concurrent apparition.
The accumulation of more zero forcing in M-BCJR algorithm is more significant and promotes the concurrent apparition.
These remarks of error possibility give an idea about the prediction of errors moments during decoding:
The presence of the competitors indicates the possibility of an erroneous decision.
The criterion of prediction can be: if the most probable competitor exceeds a threshold “Th”, then, we have to apply Z-MAP algorithm.
Finally, we note that this technique gives only a possibility of error instant.
4. The Proposed Algorithm: Z-MAP
When we locate the error instant, we have to delete the reason of this degradation. Our Z-MAP algorithm consists to increase the states number around this instant. We
Figure 4. Difference between real alpha values of full MAP-BCJR and those of M-BCJR.
should fix a threshold “Th” for detect the event of error presence and a fixed backward “r”.
The proposed Z-MAP algorithm, consists to:
1) Locate the error moment during the progress of the M-BCJR in a direction. Let us take for example the forward direction, it means, during the calculation of alphas. Let us take “i” this moment.
2) Make a return with “i-r” in the trellis.
3) Increase 
to
, with
.
4) This increase should not exceed “2 * r”.
The following example (Figure 5(a)) shows the surviving states during the execution of the 2-BCJR of a trellis with 4 states.
Let us suppose that an error is located at moment 5, and take r = 2. We show in second part (Figure 5(b)) the procedure of the Z-MAP.
5. Z-MAP Applied to Turbo Decoding
5.1. Simulation Parameters
For simulations, we use the following conditions :
Convolutional turbocode: [1, 35/23].
Code rate: 1/3, without puncturing.
Modulation: BPSK.
Interleaver: Pseudo random (S-Random) of length 5120.
Iteration number: 5.
Performance evaluation: Simulations are stopped after 20 erroneous frames.
Complexity: 12 states , reduction with 4 states.
Z-MAP: used in second decoder with threshold Th = 10–2, and r = 3.
5.2. Performances of ZMAP Turbo Decoding
The Figure 6 shows the performance of the turbo decoder ZMAP with 12 states. The reduction is 4 states.
To show that the ZMAP is an optimal version of M-BCJR, let us plot the average number of live states.
Figure 6. Performances of Z-MAP turbo decoding.
Figure 7 shows this important parameter per iteration. We can see that we keep the same low complexity of M-BCJR at some SNR (near 0.6 dB) and after little iterations (5 iterations). At the 5th iteration, the ZMAP uses 12.3 states. So, the average cost of complexity is 0.3 states only.
To show improvement in performances, Figure 8 gives a comparison between the Full MAP-BCJR turbo decoder (optimal), turbo decoder M-BCJR (degraded performance) and the turbo decoder of the proposed algorithm (Z-MAP).
The results are unexpected. The simulation shows that the performance of the Turbo decoder Z-MAP are very close to those of Full-MAP (note that the proposed algorithm works with the reduced complexity 12.3 only). At 10–3, The loss in performances between Z-MAP and Full-MAP is 0.02 dB.
Figure 7. Average number of states of Z-MAP turbo decoding.
Figure 8. BER comparison between Full-MAP, M-BCJR and Z-MAP turbo decoding at 5th iteration.
6. Conclusions
Simulations show that the Z-MAP gives an improvement in performances of the M-BCJR with low complexity at the price of a little increase in complexity (an average of 0.3). This increase is very weak because it’s related to the error moments only. The idea of Z-MAP algorithm is very important, and it opens a new field of research in digital communications. We believe that there is an important theory which is hiding behind this story.
Finally, we can say that the Z-MAP is an optimal version of the M-BCJR algorithm.