Blocking Response Surface Designs Incorporating Neigh-bour Effects ()
1. Introduction
Response Surface Methodology (RSM) is used to explore the relationship between one or more response variable and a set of experimental variables or factors with an objective to optimize the response.
Let there be  independent variables denoted by
independent variables denoted by 
 and the response variables be
and the response variables be  and there are N observations. The response is a function of input factors, i.e.
and there are N observations. The response is a function of input factors, i.e.

where u = 1, 2, …, N,  is the level of the
is the level of the , (i = 1, 2, …, v) factor in the
, (i = 1, 2, …, v) factor in the  treatment combination,
treatment combination,  denotes the response obtained from
denotes the response obtained from  treatment combination. The function f describes the form in which the response and the input variables are related and
treatment combination. The function f describes the form in which the response and the input variables are related and  is the random error associated with the
is the random error associated with the  observation that is independently and normally distributed with mean zero and common variance
observation that is independently and normally distributed with mean zero and common variance . For details on RSM, one may refer to Khuri and Cornell [1], Myers et al. [2].
. For details on RSM, one may refer to Khuri and Cornell [1], Myers et al. [2].
In the literature, the work on RSM is done assuming observations to be independent and no effect of neighbouring units. However, plots in agricultural experiments are nearby and induce some overlap effects from neighbouring units. Hence, the response from a particular plot may not be the actual response from the plot but may be the joint effect of the treatment combination applied to same plot and the treatment combination applied to the neighbouring plots. For example, in an experimental trial when the combination of pesticides is used, wind drift may cause the effect of spray spill over to adjacent plots. It is thus important to study the response surface in the presence of neighbour effects which would result in more precise estimation of the parameters of the response surface model.
Draper and Guttman [3] suggested a general model for response surface problems in which it is anticipated that the response on a particular plot will be affected by overlap effects from neighbouring plots and the same has been illustrated.
Sarika et al. [4] studied second order response surface model with neighbour effects and the rotatability conditions were derived. Methods of obtaining designs satisfying the derived conditions were given.
Jaggi et al. [5] studied response surface model incorporating neighbour effects and the same has been illustrated. They showed that if the neighbour effect is present and is included in the model, there is a substantial reduction in the residual sum of squares and the response is predicted more precisely.
In response surface analysis, it is generally assumed that the experimental trials are carried out under homogeneous conditions. This assumption may not be valid in every experimental situation. In such circumstances, the experimental trials should be carried out in groups, or blocks so that the units within each block are homogeneous. Also when the number of runs is too large, it is very difficult to accommodate all the units in a single block. Blocking is usually beneficial where it is possible to identify groups, or blocks, of experimental units, such that within blocks the experimental units are considerably more homogeneous than the blocks themselves. This type of grouping makes it possible to eliminate from error variance a portion of variation attributable to block differences. The variation between the blocks in the experiment is accounted for by including block effects in the statistical model. The nature of the blocking variables has an important impact on the data analysis.
In this paper, we focus on the methodology for blocking in first order response surface model incorporating neighbour effects. The conditions for orthogonally blocked experiments for estimation of the parameters of the model and the conditions for the constancy of variance of the parameter estimates of the model are derived. Construction of response surface designs in blocks with neighbour effects has also been given and an example is discussed.
2. First Order Response Surface Methodology with Block Effects and Incorporating Neighbour Effects
2.1. Model and Estimation of Parameters
The first order response surface model with block effects can be written in the form
 ,
,  (1)
(1)
where f(xu) denotes the observed response value at uth experimental run, xiu is the corresponding setting of the ith input variable, δl denote the effect of the lth block (l = 1, 2, …, b), wlu is a dummy variable taking the value 1 if the uth trial is carried out in the lth block; otherwise, it is equal to zero and eu is the random error.
Incorporating neighbour effects to the given model, the above model with neighbour effects in matrix notation is
 (2)
(2)
where , where δl denotes the effect of the lth block (l = 1, 2, …,b) and W is a block-diagonal matrix of the form
, where δl denotes the effect of the lth block (l = 1, 2, …,b) and W is a block-diagonal matrix of the form , where nl is the size of the lth block (l =1, 2, …, b) such that
, where nl is the size of the lth block (l =1, 2, …, b) such that . The random error vector e is assumed to have zero mean and a variance-covariance matrix
. The random error vector e is assumed to have zero mean and a variance-covariance matrix .
. ,
,  (l = 1, 2, …, b) is a (nl + 2) × v matrix.
(l = 1, 2, …, b) is a (nl + 2) × v matrix.  = ((xiu)), i = 1, 2, …, v; u = 1, 2, …, nl for all b blocks.
= ((xiu)), i = 1, 2, …, v; u = 1, 2, …, nl for all b blocks.
 , where
, where  =
=  (l = 1, 2, …, b, s ¹ s¢ = 1, 2, …, nl) is a nl × (nl + 2) neighbour matrix (assuming same neighbour structure in the b blocks) with
(l = 1, 2, …, b, s ¹ s¢ = 1, 2, …, nl) is a nl × (nl + 2) neighbour matrix (assuming same neighbour structure in the b blocks) with
 (3)
(3)
The model given in (2) is not of full column rank since the columns of W sum to 1N. The model therefore can be written as
 (4)
(4)
where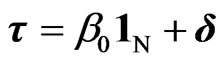 . If the columns of W are linearly independent of those of GX, then model (4) is of full rank. Thus β and τ can be uniquely estimated by the method of ordinary least squares. It is not possible to estimate β0 independent of δ unless certain constrain is imposed on the element of δ. For this purpose we can assume
. If the columns of W are linearly independent of those of GX, then model (4) is of full rank. Thus β and τ can be uniquely estimated by the method of ordinary least squares. It is not possible to estimate β0 independent of δ unless certain constrain is imposed on the element of δ. For this purpose we can assume . In this case β0 is given by
. In this case β0 is given by .
.
The Equation (4) can be written as
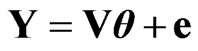 where
where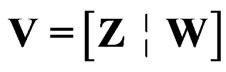 ,
,  , Zl = GlXl and
, Zl = GlXl and . The least square estimate of θ is given by
. The least square estimate of θ is given by

and the variance-covariance of  is
is

Let v = b = 2 and n1 = n2 = n. Xl (l = 1, 2) is of order (n + 2) ´ 2. Hence, . Assuming the same neighbour structure in both the blocks, the n ´ (n + 2) neighbour matrix Gl is as defined in (3).
. Assuming the same neighbour structure in both the blocks, the n ´ (n + 2) neighbour matrix Gl is as defined in (3).
Block I Block II
 ,
,  ,
,

 . Thus,
. Thus,


Therefore,
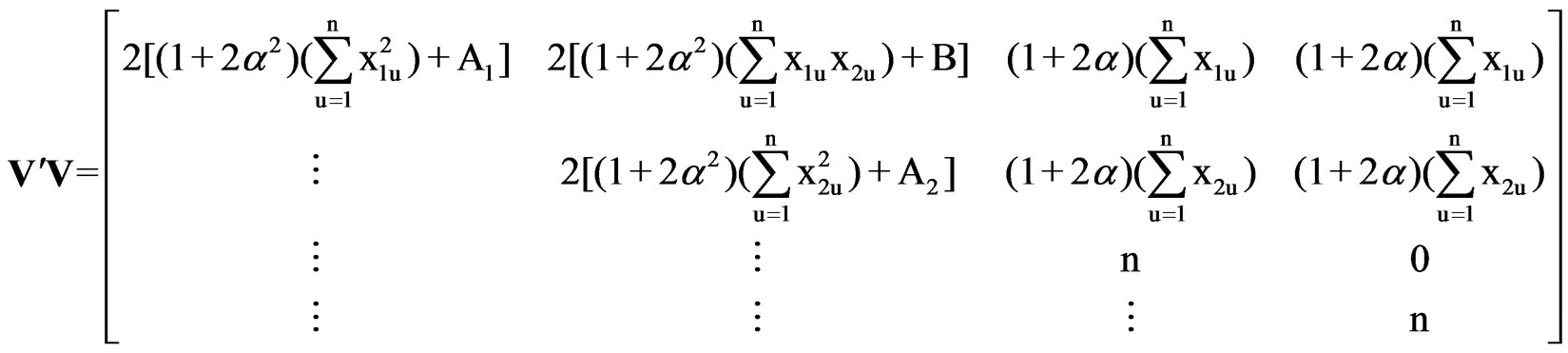
where,
 ,
, 
and

In general for v factors and for b blocks, the X matrix with two extra points as border points is

and so on

Thus, V´V is obtained as

where,


and

 .
.
2.2. Conditions for Orthogonality
To ensure orthogonality in the estimation of the parameters ,
,  has to be diagonal. This gives rise to the following conditions:
has to be diagonal. This gives rise to the following conditions:
1) 

2) 
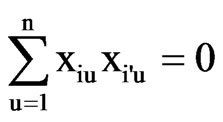
3) 
 for all blocks of size n.
for all blocks of size n.
Thus, in view of above conditions,  can be written as:
can be written as:

The normal equations for the estimation of (v + b) parameters are 
i.e., 
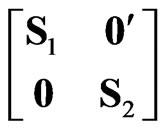 =
= 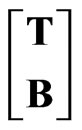 (5)
(5)
where and
and  are the parameters to be estimated.
are the parameters to be estimated.  and
and  are the vector of treatment combination totals and block totals respectively,
are the vector of treatment combination totals and block totals respectively,  and
and , i = 1, 2, …, v and l = 1, 2, ..., b.
, i = 1, 2, …, v and l = 1, 2, ..., b.


Hence,
 =
=  (6)
(6)
and
 =
= . (7)
. (7)
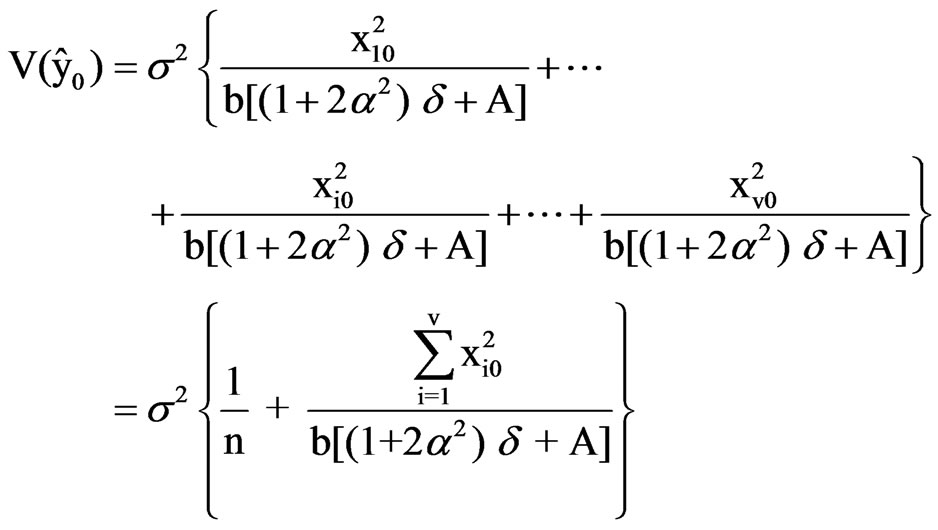
We thus obtain the variance of parameter estimates as
 and
and for i = 1, 2,…,v, and l = 1, 2, …, b. The estimated response at the point
for i = 1, 2,…,v, and l = 1, 2, …, b. The estimated response at the point  is
is 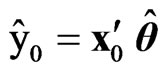 with its variance
with its variance


Thus,
 (8)
(8)
2.3. Conditions for Constancy of the Variances
The constancy of the variances of the parameter estimates is ensured by the following conditions:
1)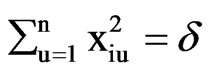 , a constant
, a constant 
2) Ai = A, a constant  for all blocks of size n.
for all blocks of size n.
Therefore,
 (9)
(9)
It is thus seen that the variances of bi’s (i = 1, 2,…, v) are same and the variance of the estimated response is a function of . For given
. For given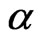 , the points for which
, the points for which  is same, the estimated response will have the same variance.
is same, the estimated response will have the same variance.
3. Method of Construction
Consider a 2v full factorial for v factors each at 2 levels and arrange the combinations in lexicographic order. Put all these runs in a single block. The second block can be obtained by circularly rotating the columns of first block once. Similarly, rotating the v columns of 2v factorial points (v – 1) times we get v × 2v design points in v blocks each of size 2v. The design so obtained satisfies all the conditions obtained in Section 2. Two extra units are added as border units in each block for neighbour effects.
Illustration
Let v = 2 (X1 and X2) with each factor at two levels, then we get four runs in full factorial. The four runs constitute the first block and the other block can be obtained by rotating the columns of the first block in a circular fashion. The various matrices are obtained as follows:
Block I Block II


 ;
; 

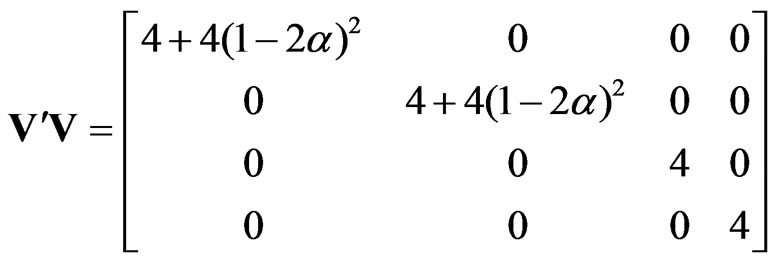
Thus,
 for i = 1, 2.
for i = 1, 2.
and
 for l = 1, 2.
for l = 1, 2.
For ,
,

Thus,
 ,
,  and
and 
Thus, it is seen that the variance of the estimated response at all points is same.
4. Conclusions
The presence of block effects in a response surface model can affect the estimation of mean response, as well as in determination of the optimum response. Hence, blocking should be done in response surfaces wherever heterogeneity among experimental units is suspected. It has also been shown that incorporating neighbour effect in a model along with block effects results in better estimates of the parameters. The developed methodology and designs can be used to fit the response surfaces with block effects and incorporating neighbour effects.
5. Acknowledgements
We are grateful to the referee and the editor for the valuable suggestions which helped in improving the quality of the paper.
[1] A. I. Khuri and J. A. Cornell, “Response Surfaces-Designs and Analysis,” Marcel Dekker, New York, 1996.
[2] R. H. Myers, D. C. Montgomery and C. M. Anderson, “Response Surface Methodology-Process and Product Optimization using Designed Experiments,” John Wiley Publication, New York, 2009.
[3] N. R. Draper and I. Guttman, “Incorporating Overlap Effects from Neighbouring Units into Response Surface Models,” Applied Statistics, Vol. 29, No. 2, 1980, pp. 128-134. doi:10.2307/2986297
[4] Sarika, S. Jaggi and V. K. Sharma, “Second Order Response Surface Model with Neighbour Effects,” Communications Statistics: Theory and Methods, Vol. 38, No. 9, 2009, pp. 1393-1403.
[5] S. Jaggi, A. Sarika and V. K. Sharma, “Response Surface Analysis Incorporating Neighbour Effects from Adjacent Units,” Indian Journal of Agricultural Sciences, Vol. 80, No. 8, 2010, pp. 719-723.