1. Introduction
Inference for the difference of two independent normal means is omnipresent in statistical practice and is introduced in most introductory staitstics texts. Typically, the variances are assumed to be unknown and must be estimated. When we assume equal variances, then a pooled estimate of the common variance is used and the test statistic is exactly distributed as a t-distribution. However, without making the equality of variances assumption, the problem is then the well-known Behrens-Fisher problem, where no exact distribution of the test statistic is available. Although there exists many approximate solutions for this problem, most statistical software packages use the Satterthwaite solution, where the test statistic is approximately distributed as a t-distribution. Maity & Sherman [1] considered the Behrens-Fisher problem with an additional assumption that one of the variances is known, and a Satterthwaite type solution is obtained. Wong & Wu [2] examined the problem considered by Maity & Sherman [1] and derived a likelihood based asymptotic solution, which has excellent coverage property.
Schechtman & Sherman [3] also considered the Behrens-Fisher problem but with an assumption that the ratio of the two variances is known. This problem arises in many practical situations. For example, when two instruments report averaged responses of the same object based on a different number of replicates, the ratio of the variances of the response is then known, and is the ratio of the number of replicates going into each response. Schechtman & Sherman [3] showed that their proposed solution is equivalent to the one suggested by Sprott & Farewell [4].
In this paper, we followed the approach by Wong & Wu [2] and obtained a likelihood based asymptotic solution for the problem considered in Schechtman & Sherman [3]. The underlying theories of the proposed method are discussed in Wong & Wu [2]. Simulation results showed that the proposed solution has excellent coverage property even for small sample sizes. The proposed method is then applied to the Behrens-Fisher problem. Again, simulation results showed the excellent coverage property of the proposed method.
The structure of the paper is as follows. Likelihood based inference for a scalar canonical parameter of the exponential family model is presented in a step-by-step algorithm in Section 2. The proposed method is applied to obtain inference for the difference of two independent normal means with known ratio of variances in Section 3. Simulation results are also recorded in Section 3 to illustrate the coverage properties of the proposed method. The proposed method is then applied to the BehrensFisher problem in Section 4. Simulation results recorded in Section 4 showed that the proposed method and the Satterthwaite method have similar coverage properties. Some concluding remarks are given in Section 5.
2. An Algorithm to Obtain Confidence Interval for a Scalar Parameter of Interest
Let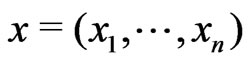 
be a sample from an exponential family model with density
where 
is the canonical parameter, and 
is a minimal sufficient statistic. Also let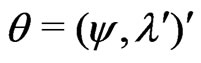 
where 
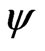is the scalar parameter of interest and 
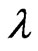is the vector nuisance parameter. Two widely used methods for inference concerning 
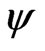are based on the Wald statstic and the signed log-likelihood ratio statistic. It is well-known that
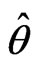, the maximum likelihood estimate of
, is asymptotically distributed as a normal distribution with mean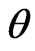 
and that the asymptotic variance can be estimated by the inverse of either the expected Fisher information matrix or the observed information matrix evaluated at
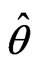. Hence a 
confidence interval for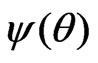 
based on the Wald statistic is
where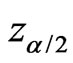 
is the 
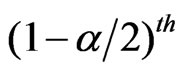percentile of
, 
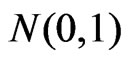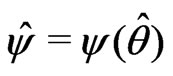, and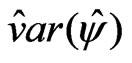 
is the estimated asymptotic variance of
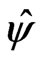, which can be derived from the asymptotic variance of 
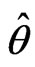using the Delta method. Alternatively, the signed log-likelihood ratio statistic
is also asymptotically distributed as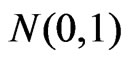 
with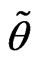 
being the constrained maximum likelihood estimate of 
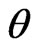for a given
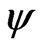. Therefore a 
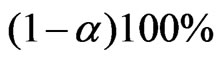confidence interval for 
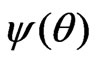based on the signed log-likelihood ratio statistic is
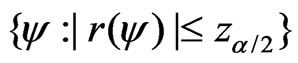
In this paper, we consider the method discussed in Wong & Wu [2], which can be summarized into the following algorithm:
Given:
a) A sample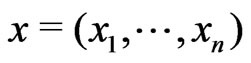 
from an exponential family model.
b) Log-likelihood function of the model is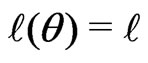 
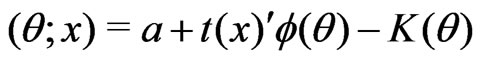where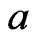 
is an additive constant that does not depend on
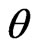, and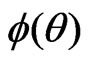 
is the canonical parameter.
Aim: Inference for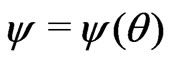
.
Step 1:
a) Obtain the overall maximum likelihood estimate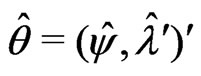 
by solving
.
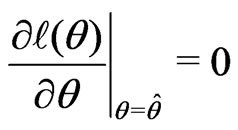b) Obtain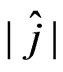
, the determinant of the observed information matrix evaluated at
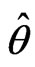, where
.
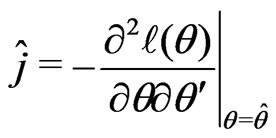c) Obtain the constrained maximum likelihood estimate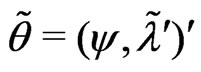 
at a fixed 
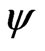by solving
.
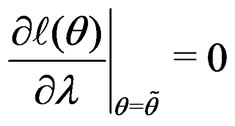d) Obtain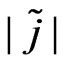
, the determinant of the observed nuisance information matrix evaluated at
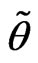, where
.
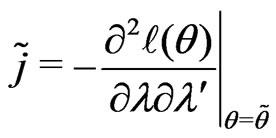Step 2: Calculate the signed log-likelihood ratio statistic
Under regularity conditions as given in DiCiccio et al [5],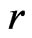 
is asymptotically distributed as 
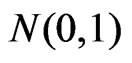with order of convergence
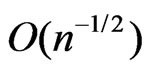. Hence a 
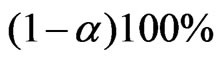confidence interval of 
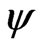is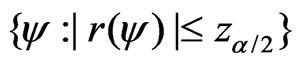
, where 
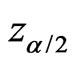is the 
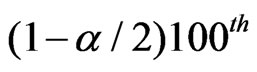percentile of
.
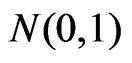Step 3: With the canonical parameter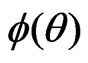
, calculate
a) 
b)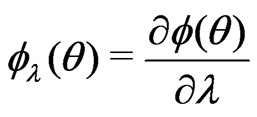 
c)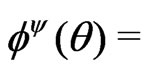 
first row of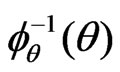 
Step 4: Parameter of interest and its variance in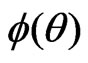 
space are
a)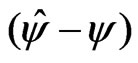 
calculated in 
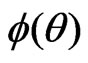space is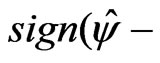 
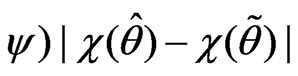where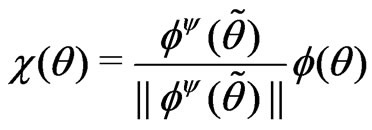
.
b)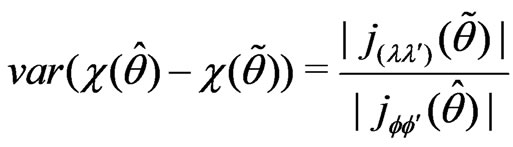 
where
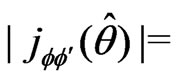
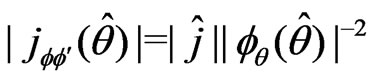and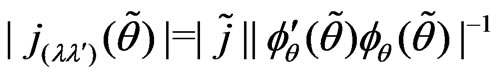
.
Step 5. The standardized maximum likelihood departure in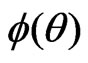 
space is
Step 6: The modified signed log-likelihood ratio statistic is
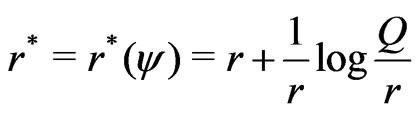
which is shown in Barndorff-Nielsen [6,7] and Wong & Wu [2] to be distributed as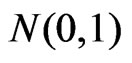 
with order of convergence
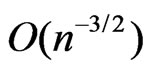. Hence a 
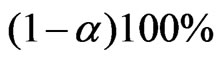confidence interval of 
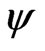is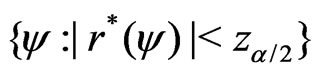
.
3. Inference for the Difference of Two Independent Normal Means with a Known Ratio of Variances
3.1. Proposed Likelihood Based Inference
Let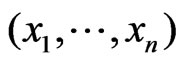 
and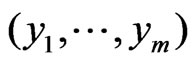 
be samples from two independent normal distributions with mean and variance 
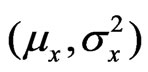and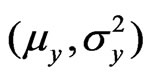 
respectively. Assume 
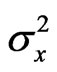and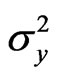 
are unknown parameters but 
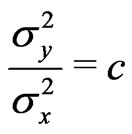is known. Schechtman & Sherman [3] showed that a 
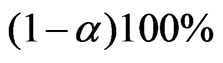confidence interval for 
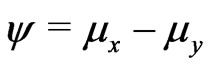can be obtained by
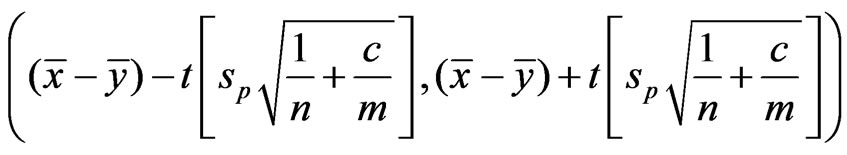
where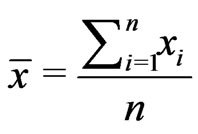
, 
, 
, 
, 
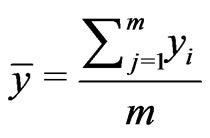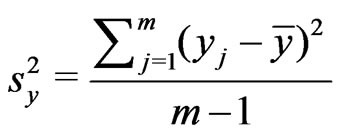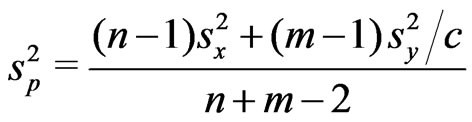, and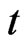 
is the 
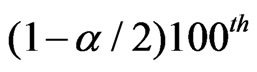percentile of the t-distribution with 
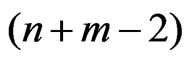degrees of freedom.
The log-likelihood function can be written as
(1)
where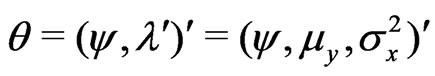
. Following the algorithm given in Section 2, we have:
Step 1:
a)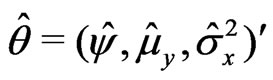 
where
, 
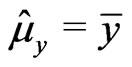, and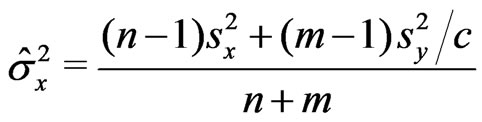
.
b) 
c)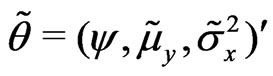 
where 
and
.
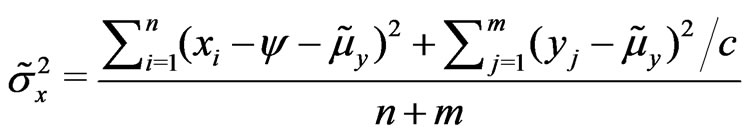d)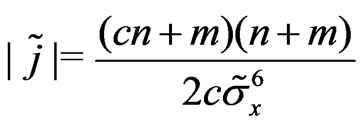
.
Step 2: 
can be obtained.
Step 3: For this problem, the canonical parameter is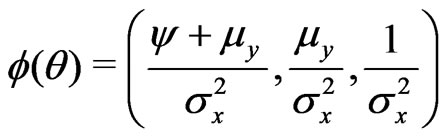
. Hence, we have a)
.
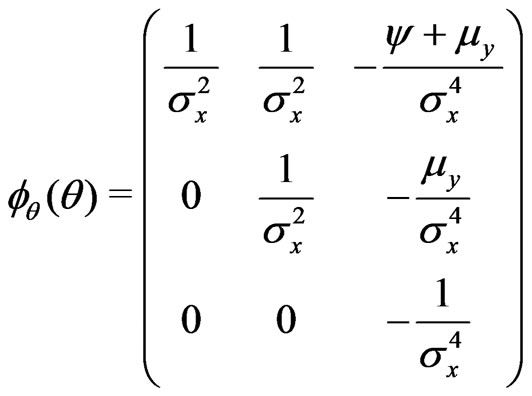b)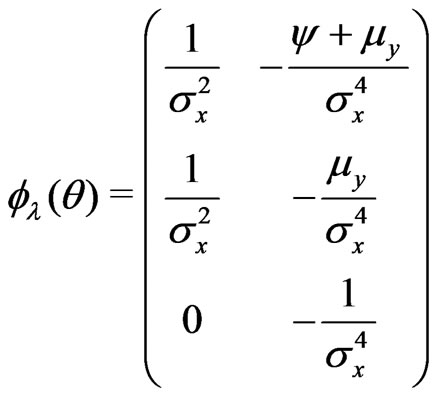
.
c)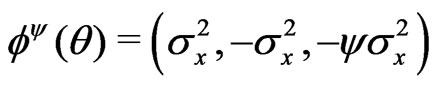
.
The rest of the steps can be obtained from the above information. Hence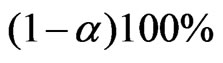 
confidence interval can be obtained from the modified signed log likelihood ratio statistic.
3.2. Simulation Study
To compare the accuracy of the proposed method with the signed log likelihood ratio method, and the Schechtman & Sherman [3] method, Monte Carlo simulation studies were conducted. We generated 10,000 simulated samples for some combinations of the parameters. For each simulated sample, we calculate the 95% confidence intervals for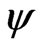 
obtained by the proposed method (
) with the signed log-likelihood ratio method (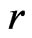
), and the Schechtman & Sherman [3] method (
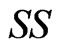). For each simulated setting, we report the proportion of 
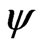that falls outside the lower bound of the confidence interval (lower error), the proportion of 
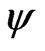that falls outside the upper bound of the confidence interval (upper error), and the proportion of 
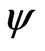that falls within the confidence interval (central coverage). The nominal values for the central coverage, and the lower and upper errors are 0.95, 0.025, and 0.025 respectively. The simulation standard errors for these three quantities are 0.0022, 0.0016 and 0.0016 respectively. Results are recorded in Tables 1-3. It is clear that the results from signed log-likelihood method are not satisfactory especially when the sample sizes are small. Results from the Schechtman & Sherman [3] method and the proposed method are almost indistinguishable even for small sample sizes (they are all within 3 simulated standard errors). The major difference between the two methods is that Schechtman & Sherman [3] method is tailor-made for this problem and cannot be applied when 
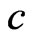is unknown; whereas the proposed method can be applied to the 
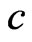is unknown case.
4. Inference for the Difference of Two Independent Normal Means with an Unknown Ratio of Variances
4.1. Proposed Likelihood Based Inference
In this section, we consider the same model set up as in Section 3, but the ratio of variances is unknown. This is the Behrens-Fisher problem, and no exact distribution of the test statistic is available. The most common approximate solution is the Satterthwaite solution, which is discussed in most of the introductory statistics texts, and it is implemented in most statistical software packages.
For this problem, the log likelihood function can be written as
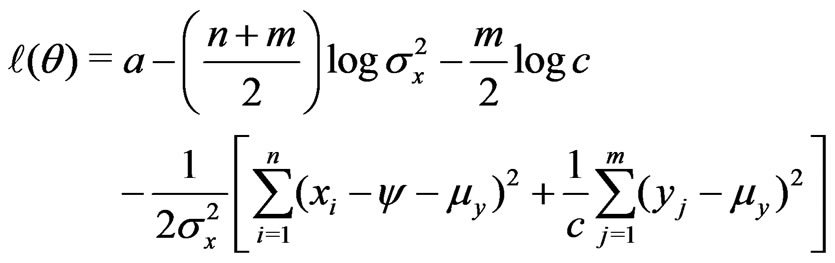(2)
where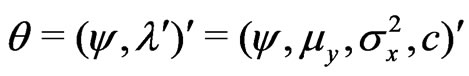
. Again, following the algorithm given in Section 2, we have Step 1:
a)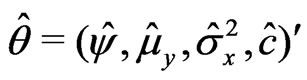 
where
, 
, 
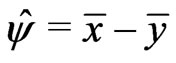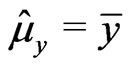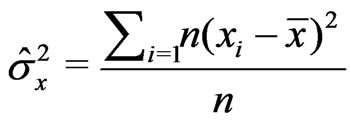, and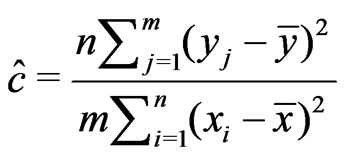
.
b)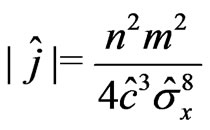 
c) The constrained maximum likelihood estimate of 
for a given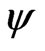
, 
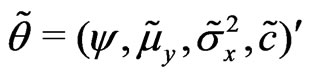does not have a closed form. However, it can be obtained by the following iterative procedure:
i) Set 
ii) Then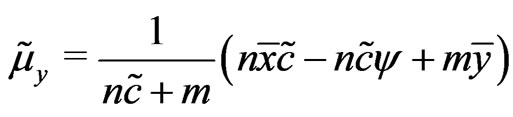
, and
iii) 
iv) Update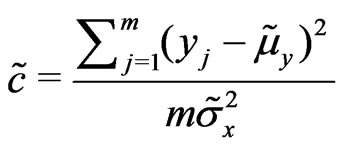
.
v) Go to ii). Will stop when the absolute value of the difference of two consecutive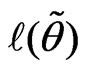 
is less than some pre-set tolerance level.
d) Since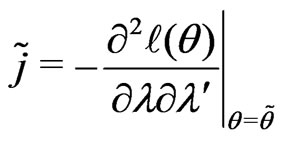
, 
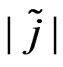can be obtained.
Step 2: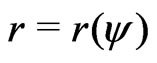 
can be obtained.
Step 3: For this problem, the canonical parameter is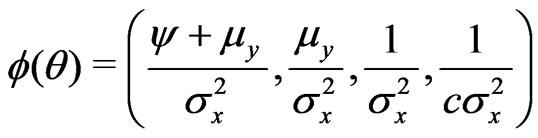
. Hence, we have
a)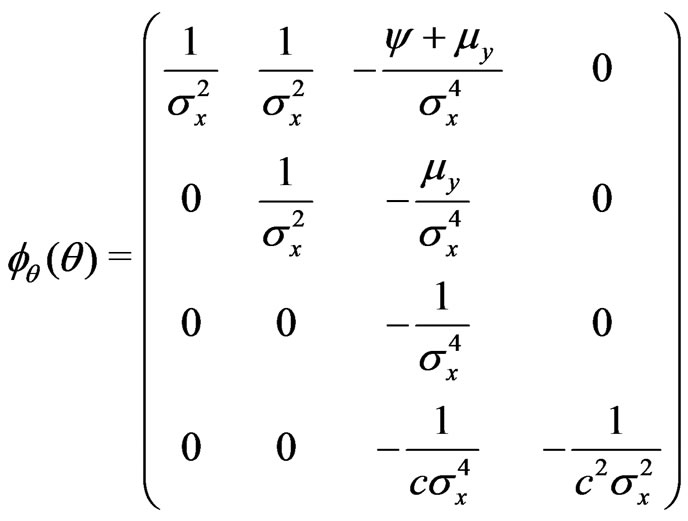
.
b)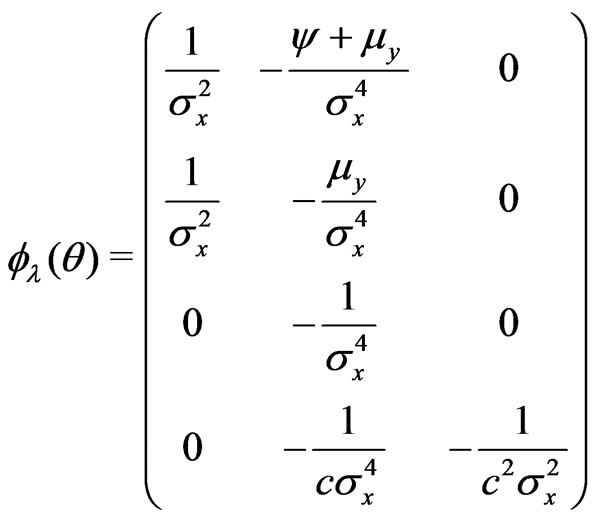
.
c)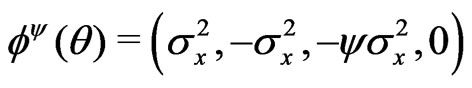
.
The rest of the steps can be obtained from the above information. Hence 
confidence interval can be obtained from the modified signed log-likelihood ratio statistic.
4.2. Simulation
Monte Carlo simulation studies, with setting being the same as those considered in Section 3, were conducted to compare the coverage properties of the proposed method (
) with the signed log-likelihood ratio method (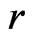
). Results are recorded in Tables 4-6 and they are similar to what we have observed in Section 3: the signed log-likelihood method does not have good coverage properties, whereas the proposed method have coverages very closed to the nominal levels.
5. Discussion
A likelihood based method to obtain inference for the
difference of two independent normal means with known ratio of variances is proposed. Monte Carlo simulation results showed that the proposed method and the Schechtman & Sherman [3] method are almost indistinguishable. However, Schechtman & Sherman [3] method is tailored made for this particular problem and cannot be applied to the case where the ratio of variances is unknown. On the other hand, the proposed method can still be applied to the unknown ratio of variance case. Simulation studies for other combinations of the parameters have also been conducted and results are consistent with those reported in this paper. A simple 
program to perform the calculations is available upon request. As a final note, the theoretical accuracy of the modified signed log-likelihood method is shown in BarndorffNielsen [5,6] and Wong & Wu [2].
[1] A. Maity and M. Sherman, “The Two Sample t-Test with One Variance Unknown,” The American Statistician, Vol. 60, No. 2, 2006, pp. 163-166. doi:10.1198/000313006X108567
[2] A. Wong and Y. Wu, “Likelihood Analysis for the Difference in Means of Two Independent Normal Distributions with One Variance Unknown,” Journal of Statistical Research, Vol. 42, 2008, pp. 17-35.
[3] E. Schechtman and M. Sherman, “The Two-sample t-Test with a Known Ratio of Variances,” Statistical Methodology, Vol. 4, No. 4, 2007, pp. 508-514. doi:10.1016/j.stamet.2007.03.001
[4] D. A. Sprott and V. T. Farewell, “The Difference between Two Normal Means,” The American Statistician, Vol. 47, No. 2, 1993, pp. 126-128. doi:10.2307/2685194
[5] O. E. Barndorff-Nielsen, “Inference on Full and Partial Parameters, Based on the Standardized Signed Log-likelihood Ratio,” Biometrika, Vol. 73, 1986, pp. 307-322.
[6] O. E. Barndorff-Nielsen, “Modified Signed Log-likelihood Ratio,” Biometrika, Vol. 78, No. 3, 1991, pp. 557- 563. doi:10.1093/biomet/78.3.557
[7] T. DiCiccio, C. Field and D. A. S. Fraser, “Approximation of Marginal Tail Probabilities and Inference for Scalar Parameters,” Biometrika, Vol. 77, 1990, pp. 77-95. doi:10.1093/biomet/77.1.77