Lindblad Equation for Harmonic Oscillator: Uncertainty Relation Depending on Temperature

Boris V. Bondarev

Moscow Aviation Institute, Moscow, Russia.

DOI: 10.4236/am.2017.811111                

Abstract

Specific nonequilibrium states of the quantum harmonic oscillator described by the Lindblad equation have been hereby suggested. This equation makes it possible to determine time-varying effects produced by statistical operator or statistical matrix. Thus, respective representation-varied equilibrium statistical matrixes have been found. Specific mean value equations have been found and their equilibrium solutions have been obtained.

Keywords

Statistical Operator, Density Matrix, Lindblad Equation, Harmonic Oscillator

1. Lindblad Equation

Statistical operator $\hat{\varrho }$ or density matrix is basically applied as the quantum mechanics tool, any information of the nonequilibrium process proceeding within the tested system may be gained from [1] [2] [3] [4] [5] . When the process concerned proceeds within the system which fails interacting with its environment, statistical operator $\hat{\varrho }$ will satisfy Liouville-von Neumann equation as follows:

$i\hslash \stackrel{\dot{}}{\hat{\varrho }}=\left[\hat{H}\hat{\varrho }\right]$ . (1.1)

With provision for the fact that the system interacts with any environment, a new equation shall be produced [4] - [18] . Lindblad is the first one who offered the equation describing interaction of the system with a thermostat [11] . This work is devoted to Markovian equation, which hereby describes nonequilibrium quantum harmonic oscillator performance.

We will write the kinetic equation for a quantum harmonic oscillator as follows:

$i\hslash \stackrel{\dot{}}{\hat{\varrho }}=\left[\hat{H}\hat{\varrho }\right]+i\hslash A\left(\left[\hat{a}\hat{\varrho },{\hat{a}}^{+}\right]+\left[\hat{a},\hat{\varrho }{\hat{a}}^{+}\right]\right)+i\hslash B\left(\left[{\hat{a}}^{+}\hat{\varrho },\hat{a}\right]+\left[{\hat{a}}^{+},\hat{\varrho }\hat{a}\right]\right)$ , (1.2)

where

$\hat{H}=\hslash \omega \left({\hat{a}}^{+}\hat{a}+1/2\right)$ , (1.3)

A and B are constants. Operator $\hat{a}$ is formulated as follows:

$\hat{a}=\left(i\hat{p}/\sqrt{m}+\sqrt{\kappa }\hat{x}\right)/\sqrt{2\hslash \omega }$ , (1.4)

where

$\omega =\sqrt{\kappa /m}$ .

Equation (1.2) is very precise to describe time varying state of the thermostat-interacted quantum harmonic oscillator and its equilibrium state.

2. Energy Representation

Now, we will define the wave functions describing specific energy state ${\phi }_n\left(x\right)$ . The very functions satisfy the equation as follows:

$\hat{H}{\phi }_n\left(x\right)=E_n{\phi }_n\left(x\right)$ , (2.1)

where

$E_n=\hslash \omega \left(n+1/2\right)$ , (2.2)

$n=0,1,2,\cdots$

As referred to energy representation, the matrix elements of statistical operator $\hat{\varrho }$ will be formulated by the equation as follows:

${\varrho }_{m{n}^{\prime }}={\displaystyle \int {\phi }_n^{*}\left(x\right)\hat{\varrho }{\phi }_{n^{\prime }}}\left(x\right)dx$ . (2.3)

Wave functions satisfy the following equations:

$\hat{a}{\phi }_n=\sqrt{n}{\phi }_{n-1},{\hat{a}}^{+}{\phi }_n=\sqrt{n+1}{\phi }_{n+1}$ . (2.4)

With provision for the above formulas the following matrix-formed equation (1.2) is derived:

$\begin{array}{l}{\stackrel{\dot{}}{\varrho }}_{n{n}^{\prime }}=-i\omega \left(n-n^{\prime }\right){\varrho }_{n{n}^{\prime }}+A\left[2\sqrt{\left(n+1\right)\left(n^{\prime }+1\right)}{\varrho }_{n+1,n^{\prime }+1}-\left(n+n^{\prime }\right){\varrho }_{n{n}^{\prime }}\right]\\ +B\left[2\sqrt{n{n}^{\prime }}{\varrho }_{n-1,n^{\prime }-1}-\left(n+n^{\prime }+2\right){\varrho }_{n{n}^{\prime }}\right].\end{array}$ (2.5)

Now, we will write the equation for diagonal elements of density matrix ${\varrho }_{nn}=w_n$ , where $w_n$ is the probability referred to oscillator state ${\phi }_n$ . The equation produced has the form as follows:

${\stackrel{\dot{}}{w}}_n=2A\left[\left(n+1\right)w_{n+1}-n{w}_n\right]+2B\left[n{w}_{n-1}-\left(n+1\right)w_n\right]$ . (2.6)

This kinetic equation describes particular harmonic oscillator state transitions. In this case, there may be gained coefficients A and B as follows:

$A=\left(1/2\right)P\exp \left(\beta \hslash \omega /2\right),B=\left(1/2\right)P\exp \left(-\beta \hslash \omega /2\right)$ , (2.7)

where P is probability of transition per unit time; $\beta =1/\left(k_{B}T\right)$ is reciprocal temperature.

Equation (2.6) has specific oscillator state equilibrium distribution, which satisfies the following equation:

$A\left[\left(n+1\right)w_{n+1}-n{w}_n\right]+B\left[n{w}_{n-1}-\left(n+1\right)w_n\right]=0$ . (2.8)

This equation is solved by the method as follows:

$w_n=\left(1-q\right)q^n$ (2.9)

under the following condition

$q=B/A=\exp \left(-\beta \hslash \omega \right)$ . (2.10)

3. Mean Value of Coordinate

Mean value $\bar{b}$ assigned by operator $\hat{b}$ is defined as

$\bar{b}=Tr\left(\hat{b}\hat{\varrho }\right)$ . (3.1)

For gaining mean value $\bar{a}$ the respective equation may be derived from Formula (1.2). Using the equality of:

$\hat{a}{\hat{a}}^{+}-{\hat{a}}^{+}\hat{a}=1$ , (3.2)

we will get the equation as follows:

$\stackrel{\dot{}}{\bar{a}}=\left(-i\omega -A+B\right)\bar{a}$ . (3.3)

Now, we can find the derivatives from mean values $\bar{x}$ and $\bar{p}$ . By applying Formula (1.4) we will get:

$i\stackrel{\dot{}}{\bar{p}}/\sqrt{m}+\sqrt{\kappa }\stackrel{\dot{}}{\bar{x}}=\left(-i\omega -A+B\right)\left(i\bar{p}/\sqrt{m}+\sqrt{\kappa }\bar{x}\right)$ .

Then, we will try to equate both the real and imaginary parts of this equation:

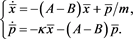(3.4)

If we eliminate $\bar{p}$ from this set of equations, we can obtain the mean coordinate equation

$\ddot{\stackrel{¯}{x}}+2\left(A-B\right)\stackrel{\dot{}}{\bar{x}}+\left[{\omega }^2+{\left(A-B\right)}^2\right]\bar{x}=0$ . (3.5)

The above Equation (3.5) provides the following solution:

$\bar{x}\left(t\right)=\left(C_1\cos \omega t+C_2\sin \omega t\right)\exp \left[-\left(A-B\right)t\right]$ , (3.6)

where $C_1$ and $C_2$ are arbitrary constants.

4. Mean Oscillator Energy

Now, we will find the time derivative from $\overline{a^{+}a}$ . By applying the above equality (3.2) we will produce the following derivative from Equation (1.2):

$\stackrel{.}{\stackrel{¯}{a^{+}a}}+2\left(A-B\right)\overline{a^{+}a}=2B$ . (4.1)

We can define harmonic oscillator time-varying energy effects inserting the following formula in Equation (4.1):

$\overline{a^{+}a}=\bar{H}/\left(\hslash \omega \right)-1/2$ .

Thus, the following differential equation is derived:

$\stackrel{\dot{}}{\bar{H}}+2\left(A-B\right)\bar{H}=\hslash \omega \left(A+B\right)$ . (4.2)

The solution of the equation is:

$\begin{array}{l}\bar{H}\left(t\right)=C\exp \left[-2\left(A-B\right)t\right]\\ +\left[\hslash \omega \left(A+B\right)\right]/\left[2\left(A-B\right)\right]\end{array}$ , (4.3)

where C is an arbitrary constant. The Equation (4.2) has specific stationary solution:

$\bar{H}=\left[\hslash \omega \left(A+B\right)\right]/\left[2\left(A-B\right)\right]$ . (4.4)

Since constants A and B are related (2.7), the stationary solution obeys the formula as follows:

$\bar{H}=\left[\hslash \omega \left(e^{\beta \hslash \omega }+1\right)\right]/\left[2\left(e^{\beta \hslash \omega }-1\right)\right]=\left(\hslash \omega /2\right)cth\left(\beta \hslash \omega /2\right)$ . (4.5)

If T = 0, then $\bar{H}=\left(\hslash \omega /2\right)$ . If T increases to infinity, then $\bar{H}=k_{B}T$ .

5. Kinetic Equation Expressed in Terms of Coordinate and Momentum Operators

Let us express the Equation (1.2) in terms of operators $\hat{x}$ and $\hat{p}$ . For this purpose, we will firstly write the Equation (1.2) as follows:

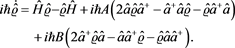(5.1)

Since the energy operator is equal to:

$\hat{H}={\hat{p}}^2/\left(2m\right)+\kappa {\hat{x}}^2/2$ , (5.2)

we will insert it in Equation (5.1) along with Formula (1.4) to obtain the following one:

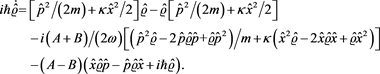(5.3)

6. Coordinate Representation

In coordinate representation the density matrix looks like this: $\varrho =\varrho \left(t,x,x^{\prime }\right)$ . The coordinate and momentum operators are:

$\hat{x}=x,\hat{p}=-i\hslash {\partial }_x$ .

Using the above values we can write Equation (5.3) by the formula as follows:

$\begin{array}{l}{\partial }_t\varrho =i\hslash /\left(2m\right)\left({\partial }_x^2-{\partial }_{x^{\prime }}^2\right)\varrho -i\kappa /\left(2\hslash \right)\left(x^2-{x^{\prime }}^2\right)\varrho \\ +\left(A+B\right)/\left(2\hslash \omega \right)\left[{\hslash }^2{\left({\partial }_x-{\partial }_{x^{\prime }}\right)}^2/m-\kappa {\left(x-x^{\prime }\right)}^2\right]\varrho \\ +\left(A-B\right)\left(1+x{\partial }_{x^{\prime }}+x^{\prime }{\partial }_x\right)\varrho .\end{array}$ (6.1)

Physical interpretation of density matrix implies that the following expression

$w\left(t,x\right)=\varrho \left(t,x,x\right)$ (6.2)

is the probability density.

Let us introduce new variables

$x_1=\left(x+x^{\prime }\right)/2,x_2=x-x^{\prime }$ . (6.3)

In this case

${\partial }_x=\left({\partial }_1+{\partial }_2\right)/2,{\partial }_{x^{\prime }}=\left({\partial }_1-{\partial }_2\right)/2$ .

Referring to density matrix and using the above new variables we will get the equation as follows:

$\begin{array}{l}{\partial }_t\varrho =i\hslash /m{\partial }_1{\partial }_2\varrho -i\kappa /\hslash x_1{x}_2\varrho \\ +\left(A+B\right)/\left(\hslash \omega \right)\left[{\hslash }^2/\left(2m\right){\partial }_1^2\varrho -\kappa /2x_2^2\varrho +\epsilon \left(1+x_1{\partial }_1-x_2{\partial }_2\right)\varrho \right],\end{array}$ (6.4)

where

$\epsilon =\hslash \omega \left(A-B\right)/\left(A+B\right)=\hslash \omega \text{th}\left(\beta \hslash \omega /2\right)$ . (6.5)

In this case

. (6.6)

We will find the solution of Equation (6.4) as follows:

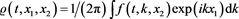. (6.7)

Reciprocal transformation

$f\left(t,k,x_2\right)=f\varrho \left(t,x_1,x_2\right)\exp \left(-ik{x}_1\right)\text{d}{x}_1$ . (6.8)

Taking into account (6.6) we will obtain:

$f\left(t,0,0\right)=f\varrho \left(t,x,0\right)\text{d}x={\displaystyle \int w\left(t,x\right)\text{d}x=1}$ . (6.9)

Thus, in view of function (6.8) the following equation is formed:

$\begin{array}{l}{\partial }_{t}f=-\hslash k/m{\partial }_{x}f+\kappa /\hslash x{\partial }_{k}f\\ -\left(A+B\right)/\left(\hslash \omega \right)\left[{\hslash }^2{k}^2/\left(2m\right)+\kappa x^2/2+\epsilon \left(k{\partial }_k+x{\partial }_x\right)\right]f.\end{array}$ (6.10)

This equation has an equilibrium solution which satisfies both equations as follows:

$-\hslash k/m{\partial }_{x}f+\kappa /\hslash x{\partial }_{k}f=0$ , (6.11)

${\hslash }^2{k}^{2}f/\left(2m\right)+\kappa x^{2}f/2+\epsilon \left(k{\partial }_k+x{\partial }_x\right)f=0$ . (6.12)

We will write the performance equation of the above Formula (6.11):

$-m\text{d}x\left({\hslash }^{2}k\right)=x\text{d}k/\kappa$ .

This equation has the solution as follows:

${\hslash }^2{k}^2/\left(2m\right)+\kappa x^2/2=\text{const}$ .

This formula implies that the general solution of Equation (6.11) takes the form as follows:

$f=f\left(E\right)$ ,

where

$E={\hslash }^2{k}^2/\left(2m\right)+\kappa x^2/2$ .

We put this function into Equation (6.12) to get the following formula:

$\text{d}f/\text{d}E+f/\left(2\epsilon \right)=0$ .

Taking into account condition (6.9) this equation has the following solution:

$f\left(E\right)=\exp \left[-E/\left(2\epsilon \right)\right]$ .

Thus, the equilibrium solution of Equation (6.10) takes the form as follows:

$f\left(k,x\right)=\exp \left\{-\left[{\hslash }^2{k}^2/\left(2m\right)+\kappa x^2/2\right]/\left(2\epsilon \right)\right\}$ . (6.13)

We will find the equilibrium density matrix by formula (6.7):

$\varrho \left(x_1,x_2\right)=1/\left(2\pi \right){\displaystyle \int \exp \left\{-\left[{\hslash }^2{k}^2/\left(2m\right)+\kappa x_2^2/2\right]/\left(2\epsilon \right)\right\}}{e}^{ik{x}_1}dk$ .

Integration brings us to the formula:

$\varrho \left(x_1,x_2\right)=\sqrt{\alpha /\pi }\exp \left[-\alpha x_1^2-{\sigma }^2{x}_2^2/\left(4\alpha \right)\right]$ , (6.14)

where

$\alpha =\sigma th\left(\beta \hslash \omega /2\right),\sigma =m\omega /\hslash$ .

Using Formulas (6.3) we will get the equation as follows:

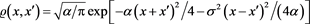. (6.15)

Using Formula (6.2) we will get equilibrium probability density [19]

$w\left(x\right)=\sqrt{\alpha /\pi }\exp \left(-\alpha x^2\right)$ . (6.16)

7. Momentum Representation

In momentum representation the coordinate and momentum operators are:

$\hat{x}=i\hslash {\partial }_p,\hat{p}=p$ .

In this representation the density matrix looks like this: $\varrho =\varrho \left(t,p,p^{\prime }\right)$ . This enables to write Equation (5.3) as follows:

$\begin{array}{l}{\partial }_t\varrho =-i/\left(2\hslash m\right)\left(p^2-{p^{\prime }}^2\right)\varrho +i\hslash \kappa /2\left({\partial }_p^2-{\partial }_{p^{\prime }}^2\right)\varrho \\ -\left(A+B\right)/\left(2\hslash \omega \right)\left[{\left(p-p^{\prime }\right)}^2/m-\kappa {\hslash }^2{\left({\partial }_p+{\partial }_{p^{\prime }}\right)}^2\right]\varrho \\ -\left(A-B\right)\left(1+p{\partial }_{p^{\prime }}+p^{\prime }{\partial }_p\right)\varrho .\end{array}$ (7.1)

Physical interpretation of density matrix $\varrho \left(t,p,p^{\prime }\right)$ implies that the expression

$w\left(t,p\right)=\varrho \left(t,p,p\right)$ (7.2)

is the probability density to detect the state when an oscillator have impulse p.

8. Wigner Function

In order to better understand the physical meaning of various kinetic state summands we will derive the equation for Wigner function $w=w\left(t,x,p\right)$ , which is a quantum analog of classical distribution function and can be defined with the use of density matrix $\varrho \left(t,x,x^{\prime }\right)$ by the relation:

$w\left(t,x,p\right)=1/\left(2\text{π}\right){\displaystyle \int \varrho }\left(t,x+\hslash q/2,x-\hslash q/2\right)\exp \left(-ipq\right)\text{d}q$ . (8.1)

If the density matrix depends on $x_1$ and $x_2$ , than

$w\left(t,x,p\right)=1/\left(2\text{π}\hslash \right){\displaystyle \int \varrho }\left(t,x_1=x,x_2\right)\exp \left(-ip{x}_2/\hslash \right)\text{d}{x}_2$ . (8.2)

Reciprocal transformation

$\varrho \left(t,x_1,x_2\right)={\displaystyle \int w}\left(t,x_1,p\right)\exp \left(ip{x}_2/\hslash \right)\text{d}p$ . (8.3)

Since there is Formula (6.9)

${\displaystyle \int \varrho }\left(t,x_1,0\right)\text{d}{x}_1=1$ ,

Wigner function satisfies the normalization requirement

${\displaystyle \int w}\left(t,x,p\right)\text{d}x\text{d}p=1$ . (8.4)

From Equation (6.4) for density matrix $\varrho \left(t,x_1,x_2\right)$ we will get the equation for Wigner function

$\begin{array}{l}{\partial }_{t}w=-p/m{\partial }_{x}w+\kappa x{\partial }_{p}w\\ +\left(A+B\right)/\left(2\hslash \omega \right)\left[{\hslash }^2/\left(2m\right){\partial }_x^{2}w+{\hslash }^2\kappa /2{\partial }_p^{2}w+\epsilon \left(2+x{\partial }_x+p{\partial }_p\right)w\right].\end{array}$ (8.5)

The equation obtained is much different from its quantum analog of Fokker- Planck equation. Summands containing derivatives ${\partial }_x^{2}w$ and ${\partial }_p^{2}w$ can be interpreted as those describing phase space diffusion. And still, it is necessary to add that it is rather hard to find physical meaning of the formula in parentheses that follows coefficient $\epsilon$ .

The equilibrium solution of Equation (8.5) should at the same time be a solution for the following equations:

$-p/m{\partial }_{x}w+\kappa x{\partial }_{p}w=0$ , (8.6)

${\hslash }^2/\left(2m\right){\partial }_x^{2}w+{\hslash }^2\kappa /2{\partial }_p^{2}w+\epsilon \left(2+x{\partial }_x+p{\partial }_p\right)w=0$ . (8.7)

General solution of the Equation (8.6) is the function:

$w=w\left(E\right)$ , (8.8)

where

$E=p^2/\left(2m\right)+\kappa x^2/2$ .

We will insert this function in Equation (8.7) and get the following equation:

$E{\text{d}}^{2}w/\text{d}{E}^2+\left(1+\mu E\right)\text{d}w/\text{d}E+\mu w=0$ , (8.9)

where

$\mu =2/\left(\hslash \omega \right)th\left(\beta \hslash \omega /2\right)$ . (8.10)

The solution of this equation is the function:

$w\left(E\right)=C{\text{e}}^{-\mu E}$ . (8.11)

Wigner function can be obtained by Formula (8.2) inserting in it equilibrium function (6.14). We have:

$w\left(x,p\right)=1/\left(2\text{π}\hslash \right)\sqrt{\alpha /\text{π}}{\displaystyle \int \exp }\left[-\alpha x^2-{\sigma }^2{x}_2^2/\left(4\alpha \right)\right]\exp \left(-ip{x}_2/\hslash \right)\text{d}{x}_2$ . (8.12)

Integration brings us to the equilibrium function

$w\left(x,p\right)=\mu \omega /\left(2\text{π}\right)\exp \left\{-\mu \left[p^2/\left(2m\right)+\kappa x^2/2\right]\right\}$ . (8.13)

This function can be represented as:

$w\left(x,p\right)=\sqrt{\alpha /\text{π}}\exp \left(-\alpha x^2\right)\sqrt{\gamma /\text{π}}\exp \left(-\gamma p^2\right)$ , (8.14)

where

$\gamma =\mu /\left(2m\right)$ . (8.15)

Let us find the mean value

$\overline{x^2}\overline{p^2}={\displaystyle \int x^2}{p}^{2}w\left(x,p\right)\text{d}x\text{d}p$ . (8.16)

Calculation gives the following formula:

$\overline{x^2}\overline{p^2}={\hslash }^2/4{\left[\left({\text{e}}^{\beta \hslash \omega }+1\right)/\left({\text{e}}^{\beta \hslash \omega }-1\right)\right]}^2$ . (8.17)

This formula leads to the following result. If T = 0, the uncertainty is equal to

$\overline{x^2}\overline{p^2}={\hslash }^2/4$ .

If $T\to \infty$ , than

$\overline{x^2}\overline{p^2}={\left(k_{B}T/\omega \right)}^2$ .

9. The Lindblad Equation Is a First Order Approximation

In work [17] it was proved that the Lindblad equation can be derived the quantum equation for a small system that interacts with the equilibrium system from the equation equations of Liouville-von Neumannas. The Lindblad equation can be written as

, (9.1)

here λ is the order parameter. Statistical operator ϱ write as well

$\hat{\varrho }={\hat{\varrho }}_0+\lambda {\hat{\varrho }}_1+\cdots$ (9.2)

Let us substitute the operator (9.2) in Equation (9.1). We have

$i\hslash {\stackrel{\dot{}}{\hat{\varrho }}}_0+\lambda {\stackrel{\dot{}}{\hat{\varrho }}}_1+\cdots =\left[\hat{H},{\hat{\varrho }}_0+\lambda {\hat{\varrho }}_1+\cdots \right]+\lambda i\hslash \hat{D}\left({\hat{\varrho }}_0+\lambda {\hat{\varrho }}_1+\cdots \right)$ . (9.3)

If the order parameter λ = 0, we get the unperturbed statistical operator ${\hat{\varrho }}_0$ :

$i\hslash {\stackrel{\dot{}}{\hat{\varrho }}}_0=\left[\hat{H}{\hat{\varrho }}_0\right]$ . (9.4)

The first value of λ, gives

$i\hslash {\stackrel{\dot{}}{\hat{\varrho }}}_1=\left[\hat{H}{\hat{\varrho }}_1\right]+i\hslash \hat{D}\left({\hat{\varrho }}_0\right)$ , (9.5)

Equilibrium values obey the equations:

$\left[\hat{H}{\hat{\varrho }}_0\right]=0$ , (9.6)

$\left[\hat{H}{\hat{\varrho }}_1\right]+i\hslash \hat{D}\left({\hat{\varrho }}_0\right)=0$ . (9.7)

Equation (9.7) is equivalent to the equation

$\hat{D}\left({\hat{\varrho }}_0\right)=0$ . (9.8)

So, the equilibrium values satisfy the following equations

$\{\begin{array}{l}\left[\hat{H}{\hat{\varrho }}_0\right]=0,\\ \hat{D}\left({\hat{\varrho }}_0\right)=0.\end{array}$ (9.9)

Examples of such equations are the Equations (6.11), (6.12) and (8.6), (8.7).

10. Conclusion

We considered the equation proposed by Lindblad for the statistical operator describing nonequilibrium state of quantum harmonic oscillator. From this equation, first we obtained the density matrix equation in energy representation and the equation for the diagonal elements of this matrix. We formulated the expressions defining physical meaning of Lindblad equation coefficients. Then we derived the equation for the mean value of a coordinate and found its general solution. We demonstrated that the mean coordinate value exponentially decreases in time. We obtained the equation for the mean oscillator energy and its general solution. We found the equilibrium mean energy value. This value is a monotonic decreasing function of temperature. We formulated Lindblad equation using coordinate and momentum operators. We obtained the density matrix equation in the coordinate representation. From this equation, we derived the formula for equilibrium density matrix. We wrote the density matrix equation in the momentum representation. We obtained Wigner function equation and found the respective equilibrium state function. We found the uncertainty relation for various temperatures by applying Wigner equilibrium function.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	von Neumann, J. (1964) Mathematical Basis of Quantum Mechanics. Nauka, Moscow.
[2]	Blokhintzev, D.I. (1961) Fundamental Quantum Mechanics. Higher School, Moscow.
[3]	Landau, L.D. and Lifshits, E.M. (1963) Quantum Mechanics. Nauka, Moscow.
[4]	Blum, K. (1981) Density Matrix Theory and Application. Plenum, New York and London. https://doi.org/10.1007/978-1-4615-6808-7
[5]	Bondarev, B.V. (2001) Density Matrix Method in Quantum Cooperative Process Theory. Sputnik+, Moscow.
[6]	Stratonovich, R.L. (1985) Nonlinear Nonequilibrium Thermodynamics. Nauka, Moscow.
[7]	Shen, Y.R. (1967) Quantum Statistics of Nonlinear Optics. Physical Review, 155, 921-931. https://doi.org/10.1103/PhysRev.155.921
[8]	Grover, M. and Silbey, R. (1970) Exciton-Phonon Interactions in Molecular Crystals. Journal of Chemical Physics, 52, 2099-2108. https://doi.org/10.1063/1.1673263
[9]	Kossakowski, A. (1972) On Quantum Statistical Mechanics of Non-Hamiltonian Systems. Reports on Mathematical Physics, 3, 247-274.
[10]	Gorini, V., Kossakowski, A. and Sudarshan, E.C.G. (1976) Completely Positive Dynamical Semigroups of N-Level Systems. Journal of Mathematical Physics, 17, 821-825. https://doi.org/10.1063/1.522979
[11]	Lindblad, G. (1976) On the Generators of Quantum Dynamical Semigroups. Communications in Mathematical Physics, 48, 119-130. https://doi.org/10.1007/BF01608499
[12]	Gorini, V., Frigerio, A., Verri, N., Kossakowski, A. and Sudarshan, E.C.G. (1978) Properties of Quantum Markovian Master Equations. Reports on Mathematical Physics, 13, 149-173.
[13]	Alicki, R. and Lendy, K. (1987) Quantum Dynamical Semigroups and Applications. Lecture Notes in Physics, Vol. 286, Springer-Verlag, Berlin. https://doi.org/10.1007/3-540-18276-4_5
[14]	Bondarev, B.V. (1991) Quantum Markovian Master Equation for System of Identical Particles Interacting with a Heat Reservoir. Physica A, 176, 366-386.
[15]	Bondarev, B.V. (1992) Quantum Markovian Master Equation Theory of Particle Migration in a Stochastic Medium. Physica A, 183, 159-174.
[16]	Bondarev, B.V. (1992) Quantum Lattice Gas. Method of Density Matrix. Physica A, 184, 205-230.
[17]	Bondarev, B.V. (1994) Derivation of Quantum Kinetic Equation from the Liouville-von Neumann Equation. Theoretical and Mathematical Physics, 100, 33-43. https://doi.org/10.1007/BF01017320
[18]	Bondarev, B.V. (2013) Quantum Markovian Kinetic Equation for Harmonic Oscilator.
[19]	Landau, L.D. and Lifshits, E.M. (1964) Statistical Physics. Nauka, Moscow.