Optimum Efficiency Analysis of Regenerative Cycle with Feed Water Heaters ()
1. Introduction
The regenerative cycle is a modified Rankine cycle which intends to improve the efficiency of the system. Baumann (1930) [1] analyzed the development of steam cycle power during years, using high steam pressure and temperature, with the objective to improve the efficiency of the power plants. In our case, we analyzed the regenerative cycle to improve the efficiency of Rankine cycle.
In the regenerative cycle, the water entering in solar collectors is hotter than the Rankine cycle and becomes better for solar power plants. The condensate of Rankine cycle at low temperature has greater irreversibility when the water is mixing in the collectors and this decreases cycle efficiency. The steam extracted from the turbine at different stages to the feed water heater with small fractions of vapor released by the turbine, reduced the irreversibility associated with the exchange of energy in the feed water heaters. The vapor or water through feed water heaters increases the average temperature of the heat source. The conditions of steam bled for each heater are selected so that the saturated steam temperature will be at 4˚C to about 100˚C higher than final condensate temperature, depending on the number of turbine extraction. It is analyzed that the thermodynamic cycle is associated to the collector’s field, looking for a way of improving its efficiency. The system is composed with the field of solar collectors, turbine, condenser, feed water heaters and pumps, as showing in Figure 1. The mass fractions (yn) are the mass relation between the mass flow extracted from the turbine and the mass fraction that crosses the solar collectors (yn = Wn/mn).
According to the capacity of the turbines, it can be divided in three categories: a) Medium capacity turbines that do not use more than 3 feed heaters; b) High pressure high capacity that does not use more than 5 to 7 feed heaters and c) Supercritical turbines that use between from 8 to 9 heaters.
There are some advantages of regenerative power cycle compared of Rankine cycle: 1) The heating process in the collectors tends to become reversible; 2) The thermal stresses in the collectors are minimized because of the water being hotter; 3) The steam condenser size can be reduced; 4) The turbine efficiency increases decreasing the turbine damage. But also there are some disadvantages as the plant become more complicated, more expensive and increase the number of maintenance.
In a regenerative cycle with superheated steam, the irreversibility of the feed water heaters are derived from mixing an undercooled liquid with two-phase
![]()
Figure 1. Regenerative cycle with several extractions of the turbine.
fluid or saturated or superheated fluid. According to Bejan (1988) [2] , due to these irreversibility, the efficiency of the regenerative cycle depends on the distribution of the turbine, that is, the temperature difference between a feed water heater and the heater adjacent. Haywood (1949) [3] affirms that the enthalpy difference in the output between each feed water heater and the heater adjacent must be constant to obtain a maximum efficiency.
Ying (1999) [4] presents a new approach for solar power utilization, i.e. using solar heat to replace the extracted steam to heat the feed water heater in the regenerative cycle plant. They analysis of a three-stage regenerative cycle plant and shows that, by using solar energy, the work generated can be increased up to 30% while the ratio of the work generated by the saved steam to the exergy supplied by the solar heat reaches 101.28%. By using low-grade thermal energy to replace the extracted steam to heat the feed water heater in the regenerative Rankine power plant, the exergy merit index of the energy hits extremely high values and is far superior to the corresponding exergy efficiencies in other power systems with the same waste heat as the heat source alone, and the aided system can run more efficiencies than the conventional regenerative Rankine plant. Then, it can be observed that the utility the Regenerative cycle with feed water heaters is important way in solar power plants.
Weir (1960) [5] also discusses the optimal distribution of feed water heater along the turbine for the regenerative cycle. In his work he distinguishes two types of extractions in the same cycle: extraction of a condensation turbine and a reheating turbine, which does not represent the proposal of this work.
Fraidenraich (2013) [6] developed an analytical modeling of direct steam generation solar power plants and they use Rankine Cycle as the power block. They choice of evaporation temperature of 290˚C in their analyses that have the advantages of near-maximum turbine work with a relatively small pressure in the collectors. The use of regenerative cycle could improve the results of efficiency and the work. This work can give an overview on conditions could use the regenerative cycle.
Figure 2 presents the diagram the entropy versus temperature of a regenerative cycle with five (5) extractions represented by five dashed line. The third heat
![]()
Figure 2. Diagram of entropy versus temperature of regenerative cycle.
exchanger is showed by 3 points: 1, 2 and 3. Point 1 indicates the inlet of the fluid extracted from the turbine which may be in the two-phase, saturated or superheated condition and which will leave at point 3, saturated liquid. Point 2 is undercooler liquid after passing through a pump. The net work cycle is represented by the area a-b-c-d-a and the heat absorbed in the collectors by area a-b-c'-d'-a. This area, a-b-c'-d'-a, would be larger without the presence of the feed water heaters of the cycle, and consequently the lower the efficiency that is the ratio of these two areas (η = (area a-b-c-d)/(area a-b-c'-d')).
2. Numerical Analysis
The proposed equation model is based on the energy and mass balance of each component of the regenerative cycle (Figure 1) and assumes the following hypotheses: 1) Expansion of vapor and pumping of water is isentropic such as the loss of pressure along the pipes. The work fluid (water) is saturated liquid at the inlet of the pumps and at the outlet of feed water heaters. The inlet conditions are the inlet and outlet pressure and superheat temperature. Thus, the equation generated for the work per unit mass of the turbine with “n” extractions (wt [kJ/kg]) is given by:
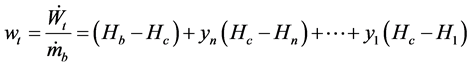 (1)
(1)
where 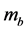 is the mass flow through the collectors [kg/s], Wt the power of the turbine [W], Hn is the enthalpy at the output of the extractions, Hb the enthalpy at the collectors output and Hc the enthalpy at the condenser inlet. The mass fraction of the “i” order extraction of the turbine is yi (i = 1 is the first extraction of the turbine) with equation:
is the mass flow through the collectors [kg/s], Wt the power of the turbine [W], Hn is the enthalpy at the output of the extractions, Hb the enthalpy at the collectors output and Hc the enthalpy at the condenser inlet. The mass fraction of the “i” order extraction of the turbine is yi (i = 1 is the first extraction of the turbine) with equation:
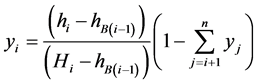 (2)
(2)
where Hi represents the enthalpy of i-order extraction from the turbine, hB(i-1) is the enthalpy at the output of each pump and hi is the enthalpy at the output of the heater. The first extraction of turbine is given by:
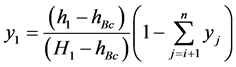 (3)
(3)
The heat per unit mass that enters the collectors (qb [J/kg]) and leaves the condenser (qc [J/kg]) is directly proportional to the enthalpy difference between the inlet and outlet of the collectors, given by:
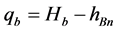 (4)
(4)
and
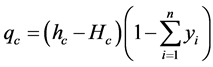 (5)
(5)
The efficiency of the cycle with “n” turbine extractions, defined by the ratio of the net work by heat entering the collectors, is calculated by the following equation:
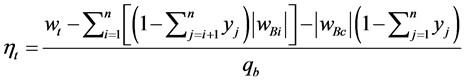 (6)
(6)
The pumps work (WBi) is the difference of output enthalpy and input enthalpy.
3. Results and Discussion
Simulations were realized with two superheating temperature (Tsup) of 400˚C and 500˚C. It was analyzed for the maximum possible efficiency and its respective work per unit of mass. When there are many extraction of turbine it can have different efficiencies, depending of the positions of the extractions in turbine. For find maximum efficiency was simulated in an interactive program that searches the maximum value in a Regenerative cycle. The software used was EES―Engineering Equation solver. The hypotheses used in the simulations are: The condensing pressure is 10 kPa for all tests; the condition of water going out of the condenser and the all feed water heaters is saturated. There is not loss pressure along of the tubes and the expansion of turbine is isentropic. If you need a non-isentropic expansion just multiply the turbine work by its isentropic efficiency which will not change the behavior of the turbine work.
Figure 3 and Figure 4 plot the maximum efficiency in function of evaporating temperature, superheating temperature and the turbine extraction number. It can note that when increase the number of extraction the maximum efficiency also increase as well as when the evaporating temperature (Tev) and superheating temperature (Tsup) is increased. The increasing of efficiency is getting smaller when the number of extraction is increased. This shows that it can be economically impracticable more than three or four extractions; the increase of efficiency is much small above four extractions.
![]()
Figure 3. Maximum efficiency of the regenerative cycle versus evaporation temperature, superheating temperature of 400˚C and number of turbine extractions.
![]()
Figure 4. Maximum efficiency of the regenerative cycle versus evaporation temperature, superheating temperature of 500˚C and number of turbine extractions.
Figure 5 and Figure 6 show the work per mass of respective maximum efficiency for superheating temperature of 400˚C and 500˚C, respectively, evaporating temperature and the number of extraction. It can be observed that there is one maximum value of work for each number of extractions. The difference of work for each evaporating temperature is decreasing when the number of extraction is increase. The work for the Rankine cycle is bigger compared with the regenerative cycle. The maximum values of Figure 5 and Figure 6 can be explained by the behavior of the mass fraction extracted from the turbine to obtain maximum efficiency, as well as the properties of the extracted fluid.
One analytical analysis for the regenerative cycle is realized to compare with numerical analysis. For the cycle of Figure 1, the balance of energy of the fist feed water heater considering the flux of mass in condenser (WC) equal 1, 0 is given by
 (7)
(7)
It can be consider as Haywood (1949) [2] that the difference of the inlet enthalpy and outlet enthalpy 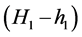 is called “t” and the difference of outlet enthalpy of heater and condensing enthalpy
is called “t” and the difference of outlet enthalpy of heater and condensing enthalpy 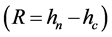 divided by the number of heater is “
divided by the number of heater is “ ”. These values t and r are considered constants. Then the mass flow for the first heater can be:
”. These values t and r are considered constants. Then the mass flow for the first heater can be:
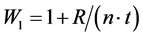 (8)
(8)
If “t” and “r” is considered constant, it could get the maximum of efficiency. The balance of energy for the second heater is given by:
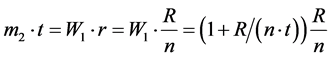 (9)
(9)
Then, the mass flow for heater number “n” can be calculated as:
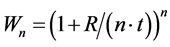 (10)
(10)
![]()
Figure 5. Work for respective maximum efficiency of the regenerative cycle versus evaporation temperature, superheating temperature of 400˚C and number of turbine extractions.
![]()
Figure 6. Work for respective maximum efficiency of the regenerative cycle versus evaporation temperature, superheating temperature of 500˚C and number of turbine extractions.
The efficiency of the cycle is calculated with the work express as the difference between the collector heat and the condenser heat that is rejected by heat absorved of collectors or:
![]() (11)
(11)
If define a preheating factor as![]() , where hb is the collector enthalpy in the saturation condition, the heat absorbed in collector can be given by about:
, where hb is the collector enthalpy in the saturation condition, the heat absorbed in collector can be given by about:
![]() (12)
(12)
where ![]() and z can be express by
and z can be express by![]() . For the efficiency to be maximum, then
. For the efficiency to be maximum, then ![]() must be maximum. Replacing the Equation (10) in Equation (12) and derivate the expression it finds:
must be maximum. Replacing the Equation (10) in Equation (12) and derivate the expression it finds:
![]() (13)
(13)
and
![]() (14)
(14)
If dQ/dz = 0 to find the maximum value of Q, it can find the following expression:
![]() (15)
(15)
Then, for n extractions of the turbine the preheating factor for the maximum efficiency is given by:
![]() (16)
(16)
That is, the efficiency of the cycle will be maximum when the preheating factor z is equal to n/(n + 1). For example, if five (5) heat exchangers were installed in the regenerative, the preheating factor would be 5/6 of the total enthalpy (hb − hc). For an infinite number of heaters in the cycle the preheating factor (z) tends to 1. Then it can replace the Equation (16) in the equation of efficiency, Equation (11), getting:
![]() (17)
(17)
Introducing![]() , (R as a function of z), the value that maximizes z, Equation (16) and substituting the difference (Hb − hn) for known values (t, n, and Rb), it finds the following expression for the efficiency that optimized regenerative cycle with n stages’ extraction:
, (R as a function of z), the value that maximizes z, Equation (16) and substituting the difference (Hb − hn) for known values (t, n, and Rb), it finds the following expression for the efficiency that optimized regenerative cycle with n stages’ extraction:
![]() (18)
(18)
Considering that Rb and t are well defined values, independent of n can be studied as the efficiency of the cycle varies according to this parameter. In the case of preheating without regeneration (n = 0), the efficiency turns out to be equal:
![]() (19)
(19)
And for a number (n) tending to infinity, the equation of efficiency is:
![]() (20)
(20)
If considering a case that Rb/t = 0.461, the efficiency for infinite extractions is![]() . The efficiency behavior for this situation can be observed in Figure 7 with the Equation (18) where the efficiency tend for 35.7%, that is the efficiency for infinite feed water heaters.
. The efficiency behavior for this situation can be observed in Figure 7 with the Equation (18) where the efficiency tend for 35.7%, that is the efficiency for infinite feed water heaters.
![]()
Figure 7. Efficiency behavior versus number of heaters.
Comparing the Figure 3 with Figure 7 it can be noted that the maximum efficiency depends of the evaporating and superheating temperature, different from analytical analysis that considering constants the value of “t” and “r”. The Table 1 shows the results of “t = Hi − hi” and “r= (hi − hc)/n” for the numerical analysis, where “i” is the order of the feed water heater. It is also present the results of ![]() to compare with the example of Figure 7.
to compare with the example of Figure 7.
The evaporating temperature that represents the situation of Figure 7 is 260˚C with the value of Rb/t = 0.461. As seen in the graph of Figure 3, the efficiency of regenerative cycle is about 48% differently of the analytical results of Equation (20) that is 35.9% for five extractions of turbine, calculated with Equation (18). Then, it can be concluded that the analytical method (considering “t” and “r” constants) with the Equation (18) is unsatisfactory because the value of t and r change with evaporating temperature, and the value of maximum efficiency is not accurate.
The pressure of extractions is also analyzed. The outlet pressure at each extraction varies with evaporation temperature (Tev) as observed in Figure 8 for superheating temperature for 400˚C and five (5) extractions. The turbine extraction pressure is given as percentages in relation to the turbine inlet pressure, i.e. pressure ratio. As an example, in the case of 5 (five) extractions, when the inlet pressure is 10 MPa the first extraction pressures along the turbine will be approximately 5500 kPa, approximately 55% of inlet pressure. For the second extraction, the pressure is approximately 2500 kPa, 25% of inlet pressure and approximately 1000 kPa (10%), 400 kPa (4%) and 100 kPa (1%) for the third, fourth and fifth feed water heaters, respectively.
It is possible to observe that, at each extraction point, the pressures extracted from the turbine have a pressure ratio not very variable along the evaporation temperature. This pressure ratio does not vary more than 5% along the evaporation temperature for the same position of extraction pressure. The pressure ratio can increase or decrease slightly along the evaporating temperature, respecting the 5% variation. This information is important for the time of simulations along the evaporating temperature.
![]()
Table 1. Results of “t” and “r” obtained in the numerical analyses for superheating of 400˚C and 4 feed water heater.
![]()
Figure 8. Ratio: inlet pressure and extraction pressure of turbine in function of evaporation temperature.
4. Conclusions
The regenerative cycle is a contribution to the Rankine cycle which intends to improve the efficiency of the thermodynamic cycle and warm the water entering in solar collectors, and become attractive for solar power plants. The maximum efficiency and turbine work of the regenerative cycle have been simulated and analyzed. The regenerative cycle uses feed water heaters to warm the water returned to the collectors. It analyzed cycle with until five feed water heaters using numerical method and compared with one analytical method. The analytical method presents an expression for maximum efficiency that can be simulated until infinite number of feed water heaters.
The results of numeric method show that the maximum efficiency increases when the number of heaters and the superheating temperature increase. The turbine works present one maximum value that depends on number of heaters, evaporating and superheating temperatures. It is also observed that the improvement of efficiency increases when the number of feed water increases.
The analytical method considers constants of the difference of enthalpy along of feed water heaters as well as between them. The results of this analytical method are unsatisfactory compared with numeric method which is more accurate. The difference of two methods can be more than 10% of difference, for example the efficiency of numerical method is 48% while the analytical method is 35.9%.
Analyzing the extractions pressure, it can be concluded that the outlet pressure at each extraction varies around five percent along the evaporation temperature. This conclusion helps the simulations to converge faster.
Acknowledgements
The authors would like to thank the Foundation of Support to Science and Technology of PE (FACEPE) for financial support.