1. Introduction
It is known that one of the key moments of the special relativity theory (SRT) is the question of the invariance of light speed and the physical sense of such invariance. Contradictory statements about this were made still by the SRT founder A. Einstein (see, for example, [1] ): “we shall, however, find in what follows, that the velocity of light in our theory plays the part, physically, of an infinitely great velocity”.
It is known that SRT is based on two postulates: the postulate of the light speed constancy and the principle of relativity, which is extended to electromagnetic phenomena [2] - [12] . Textbooks on the SRT seek the following meaning in the light speed constancy. Let the light be able to propagate in a vacuum without an intermediate medium. Since the frame of reference cannot be firmly “tied” to the emptiness, it does not matter how fast our system moves with respect to the vacuum. Consequently, the speed of light with respect to our system should allegedly be independent of the system motion. However, for some reason other particles can move in a vacuum with very different velocities. What the matter is that the other particles different from a photon? Further, for moving systems allegedly there should be a contraction of the space itself―it is the so-called kinematic effect. How can you determine the speed of this empty space itself with respect to a particular moving observer to calculate such a reduction? As one of the main confirmations of the principle of the light speed constancy, negative experiments on the detection of the ether wind are considered. So, one of the basic questions for the relativity theory: is the speed of light constant? Note that in advance to assume anything about the motion of the Earth was impossible: during the Galileo times, such experiments, for example, “could prove” that the Earth is at rest. Generally speaking, before using any “device”, it must be tested and calibrated in the laboratory to know what it measures. Imagine that someone had the false idea that, because of the Earth’s rotation around its axis, a constant wind of about 400 m/s along the parallels should be observed. Beginning to measure it with weather vanes with turntables, we found out that the wind constantly changes both in direction and in magnitude in huge limits, depending on time and place. From this, the “false conclusion” would be drawn that there is absolutely no atmosphere on the Earth.
It would seem that the answer to the question of the light speed constancy has already been given in the Michelson-Morley experiment studying the effect of the Earth motion on the speed of light. We also recall similar optical experiments made by Morley, Kennedy-Thorndike, Viennese experiment by Joose and others [13] [14] [15] . However, the term “constant” means independence on time, on spatial coordinates, on the direction of light propagation and, finally, on the properties of the light itself. It takes some effort to give an unbiased answer to the question: what could be determined in the Michelson interferometer? We note that no velocity in the Michelson experiment is measured at all, but the phase difference of the rays is measured, and we can think about speed only indirectly. Recall that two light rays moved in mutually perpendicular directions. We note, however, the following. To avoid synchronization of time intervals at different points, both these light rays moved along closed trajectories (and in two mutually perpendicular directions). Consequently, in fact, we are dealing in each of these two cases only with the “speed” of light, “averaged” for mutually opposite directions. Considering the abovementioned, it would seem that the result of Michelson’s experiment can be formulated as follows: the average speed of light of a fixed frequency for two opposite directions in a certain frame of reference does not depend on the motion of this system. No the conclusion of global constancy can be made. At least two questions would still remain in connection with the local result of the Michelson-Morley experiment: whether or not the speed of light depends on the spatial coordinates and time, and does the speed of light in a vacuum depend on the characteristics of the light itself? The result of the experiment can be theoretically analyzed both from the viewpoint of the relativity principle (by modern views in empty space) and from the viewpoint of different ideas on the properties of the ether.
The main objectives of this work are as follows:
-to give a number of theoretical remarks concerning the physical meaning of relativistic invariance;
-to analyze some theoretical ideas about the Michelson-Morley experiment;
-to critically analyze the proof of the existence of an invariant velocity.
2. General Remarks on the Relativistic Invariance
We begin with general remarks concerning the distortion of the very meaning of the invariance concept in the SRT. The wide-distributed relativistic cliche looks rather strange as if the SRT is just a new geometry, and that’s why it is allegedly consistent. There feels a clear bias toward mathematics. It must be recalled that physics is engaged in research on the causes of phenomena and specific mechanisms that directly affect the phenomenon under investigation. Of course, in order to obtain a mathematical solution, coordinate transformations are often used in physics. In essence, these are just elementary mathematical substitutions only. However, if someone claims that since the solutions are correct, then the whole Universe has really “transformed” from one area (for example, from a circle under conformal transformations) to another area, then all physicists will understand the inadequacy of such statements. It can come into mind only to the pseudo-mathematician with a sick imagination that the whole universe will contract if he does some operations with mathematical “letters”. But if some relativistic scientist says that he squeezed the entire Universe, when he went to a nearby bakery, many yes-mans will confirm this nonsense (possible, they did not read the tale “Naked King” as a child).
The existence of Lorentz transformations (published in 1900 by Larmor in the book “Ether and matter” even before the creation of the SRT) does not prove the objectivity of kinematic effects at all. First, the Lorentz transformations are not the only, but only one of many mathematical invariants of the wave equation. Prior to them, for example, the Vogt transformations were discovered, also being an invariant of the wave equation (Klein first pointed out the importance of studying group properties in 1872). Secondly, any physical principles do not follow from the mathematics itself: the invariance property is completely determined by a combination of operations and symbols in the equation. In particular, the Lorentz transformations with the speed of sound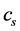 , instead of the speed of light c, can be used for some acoustic problems precisely because they are invariant (but it is obvious that no transformations of space and time are observed in this case). Thirdly, the Lorentz transformations are obtained for the process of light propagation in a vacuum. But this is a completely particular physical phenomenon, and one should not exaggerate its generality. Note that if some mathematical equation turns out to be invariant under Lorentz type transformations with some constant c’, then this only means that among the particular solutions of this equation there are “wave-type” surfaces that can propagate at a speed c’. Moreover, even the chosen equation may have other particular solutions with its own invariant transformations. But there are a lot of different mathematical equations. That is, for mathematics, no general mathematical conclusions follow from the fact of invariance. Only relativists try to “inflate a soap bubble” on such a particular phenomenon and “clone” this invariance to the properties of the whole world. Nobody makes global conclusions from the invariants of the heat equation for hydrogen or from the properties of hydrogen plasma only on the grounds that all atoms have electrons in their composition, and the nuclei have protons! The whole Universe “signalizes” that its symmetries do not coincide with the primitive spherical symmetry of point light flashes in the emptiness (look at the crystals, at living beings, at the Cosmos). Using one scalar constant c, it is impossible to determine even the speed of light in real substances-specific gases, liquids, crystals. Not to mention the fact that perturbations in the medium propagate with the speed of sound. This last speed is also not determined by a single constant, but depends on the specific substance (and may be anisotropic, for example). Apparently, in general it is impossible to fit all the properties of the world into one invariant scheme. Even for the process of light propagation, elements of the medium (atoms and molecules), possessing a huge variety of properties, are involved in the process in addition to the “properties” of the void, also interaction with devices is involved, that immediately individualizes this process. That is, there must be at least something average between the properties of the emptiness and the properties of a particular substance.
, instead of the speed of light c, can be used for some acoustic problems precisely because they are invariant (but it is obvious that no transformations of space and time are observed in this case). Thirdly, the Lorentz transformations are obtained for the process of light propagation in a vacuum. But this is a completely particular physical phenomenon, and one should not exaggerate its generality. Note that if some mathematical equation turns out to be invariant under Lorentz type transformations with some constant c’, then this only means that among the particular solutions of this equation there are “wave-type” surfaces that can propagate at a speed c’. Moreover, even the chosen equation may have other particular solutions with its own invariant transformations. But there are a lot of different mathematical equations. That is, for mathematics, no general mathematical conclusions follow from the fact of invariance. Only relativists try to “inflate a soap bubble” on such a particular phenomenon and “clone” this invariance to the properties of the whole world. Nobody makes global conclusions from the invariants of the heat equation for hydrogen or from the properties of hydrogen plasma only on the grounds that all atoms have electrons in their composition, and the nuclei have protons! The whole Universe “signalizes” that its symmetries do not coincide with the primitive spherical symmetry of point light flashes in the emptiness (look at the crystals, at living beings, at the Cosmos). Using one scalar constant c, it is impossible to determine even the speed of light in real substances-specific gases, liquids, crystals. Not to mention the fact that perturbations in the medium propagate with the speed of sound. This last speed is also not determined by a single constant, but depends on the specific substance (and may be anisotropic, for example). Apparently, in general it is impossible to fit all the properties of the world into one invariant scheme. Even for the process of light propagation, elements of the medium (atoms and molecules), possessing a huge variety of properties, are involved in the process in addition to the “properties” of the void, also interaction with devices is involved, that immediately individualizes this process. That is, there must be at least something average between the properties of the emptiness and the properties of a particular substance.
Thus, the group properties of mathematical equations, as transformations with mathematical symbols, have absolutely nothing to do with any physical principles or postulates, that is, group properties can be found without additional physical hypotheses. For example, the Lorentz transformations, reflecting the group properties of Maxwell’s equations in the emptiness (or of the classical wave equation, including in acoustics), are absolutely not connected with the postulate of light speed constancy or with the principle of relativity introduced in the SRT.
Now let us make a remark about one of the possible mathematical derivations of the Lorentz transformations. A transformation is sought that transforms the equation of one sphere (or interval) into the equation of another sphere (respectively, of another interval). Obviously, such a transformation is not the only one for four variables. First, the separate equating 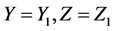 represents just one of the possible hypotheses, as well as the requirement of linearity, mutual unambiguity, reversibility, etc. For example, it is elementarily to include different functional dependencies into the transformations instead of the constant c. Secondly, any transformation of light surfaces does not at all determine the transformation of volumes in which non-electromagnetic physical processes can occur. Recall that the speed of sound also does not depend on the motion of the source, but no global conclusions about the properties of space and time follow from here. Thus, particular Lorentz transformations cannot impose any restrictions on all physics.
represents just one of the possible hypotheses, as well as the requirement of linearity, mutual unambiguity, reversibility, etc. For example, it is elementarily to include different functional dependencies into the transformations instead of the constant c. Secondly, any transformation of light surfaces does not at all determine the transformation of volumes in which non-electromagnetic physical processes can occur. Recall that the speed of sound also does not depend on the motion of the source, but no global conclusions about the properties of space and time follow from here. Thus, particular Lorentz transformations cannot impose any restrictions on all physics.
The theory of relativity is actually a “theory of visibility (only seem)”: what will we see in the experiment if the theoretical laws of electromagnetic interactions are putted in a basis of the observations (absolutization of electromagnetic phenomena). Similarly, we can raise the question of how the phenomena observed with the aid of sound, etc., will look. Of course, the finiteness of the interaction transmission rate alters the phenomena observed with the help of these interactions. But this does not prevent us from making unified extrapolations for binding to space and time (absolute classical physical concepts) for the universal description of the world, not limited by any universal hypotheses. All the kinematics of the SRT follows from the invariance of the interval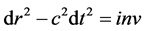 . However, we see that this expression is written for empty space. In a medium, the speed of light is not constant, it can be anisotropic, and not with arbitrary frequencies light can propagate in a given medium (recall damping, absorption, reflection, scattering). In no part of physics the properties of phenomena are determined by the properties of empty space. And only the SRT pretends to such a general “cloning” of properties.
. However, we see that this expression is written for empty space. In a medium, the speed of light is not constant, it can be anisotropic, and not with arbitrary frequencies light can propagate in a given medium (recall damping, absorption, reflection, scattering). In no part of physics the properties of phenomena are determined by the properties of empty space. And only the SRT pretends to such a general “cloning” of properties.
3. The Invariance of Maxwell Equations
Let us analyze in more detail the “fundamental” question of the invariance of the Maxwell equations, which is widely declared in the SRT. The following four equations in the differential form are attributed to the system of fundamental equations of electrodynamics in the textbook [16] :
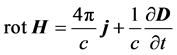 ,
, 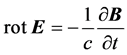
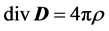 ,
, 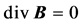
However, this system of eight equations in the coordinate form is obviously insufficient to determine the 16 quantities (with all components taken into account) E, D, B, H, j and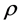 . It is also necessary to introduce the characteristics of the medium into the equations. Taking into account the existence of nonlinear, inhomogeneous, anisotropic media, it is impossible to do this in a general form. Only within certain limits we can introduce particular model representations of linear dependencies:
. It is also necessary to introduce the characteristics of the medium into the equations. Taking into account the existence of nonlinear, inhomogeneous, anisotropic media, it is impossible to do this in a general form. Only within certain limits we can introduce particular model representations of linear dependencies:
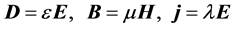
and can add 9 more equations with three new unknown functions 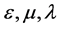 (or constants-for model assumptions) that characterize the medium. There can be no question of uniform invariance of the last three equations. We recall, for example, the existence of ferromagnets and ferroelectrics for which hysteresis is observed, that is, the course of the process depends on its prehistory. In the latter cases, behavior is not generally described by differential equations. Is it worth “to inflate the soap bubble of the SRT” only on the invariance for a part of the complete system of equations? Obviously not! Otherwise, it would be possible to select arbitrary pieces from any equation and speculate on the invariance of these terms. In addition, the Lorentz transformations (hyperbolic rotation) change the relationships between angles, hence, the change in the shape of complex boundaries must be taken into account for transition between moving frames of reference. Thus, the complete system of Maxwell’s equations in arbitrary media cannot be invariant with respect to any single physical transformation.
(or constants-for model assumptions) that characterize the medium. There can be no question of uniform invariance of the last three equations. We recall, for example, the existence of ferromagnets and ferroelectrics for which hysteresis is observed, that is, the course of the process depends on its prehistory. In the latter cases, behavior is not generally described by differential equations. Is it worth “to inflate the soap bubble of the SRT” only on the invariance for a part of the complete system of equations? Obviously not! Otherwise, it would be possible to select arbitrary pieces from any equation and speculate on the invariance of these terms. In addition, the Lorentz transformations (hyperbolic rotation) change the relationships between angles, hence, the change in the shape of complex boundaries must be taken into account for transition between moving frames of reference. Thus, the complete system of Maxwell’s equations in arbitrary media cannot be invariant with respect to any single physical transformation.
The first four equations can be of independent interest only when considering fields in the void. However, the invariance of the Maxwell equations in the void with respect to the Lorentz transformations does not mean anything at all for other phenomena. First, in an empty space, we can cut off half the segment and double it-we get the same segment. Therefore, in an empty mathematical space, you can use any frame of reference, consistent geometries and conversion factors. This can be determined only by the convenience of a mathematical description. However, the presence of real physical bodies and fields in space defines natural reference points, characteristic scales and interrelations between objects. All this determines the differences between the real physical space and the empty mathematical space. Secondly, the property of certain interactions to propagate in a vacuum at the speed of light does not determine the rate of propagation of interactions in the medium. Despite the huge role of electromagnetic interactions, perturbations in media propagate with the speed of sound. Using one scalar constant c belonged to the vacuum, it is impossible to determine the velocities of sound and light in gases, liquids and solids. For example, light of not every frequency can propagate in a medium (recall about scattering, absorption, attenuation, reflection). It is not clear how the anisotropy of real solids could arise in the initially isotropic space. All these and many other properties go beyond the applicability of the Maxwell equations in vacuum. But the SRT offers cloning spherically symmetric properties of point flashes of light in a vacuum for all properties of material bodies and media. Consequently, adjusting the properties of the whole world under the invariance of Maxwell’s equations in the void is an overestimated claim of the SRT. Thirdly, splitting the uniform (in its effect) field into electric and magnetic parts is relatively arbitrary, and the invariance of these artificially splitted parts cannot be of decisive importance.
Let’s give some important remark. Maxwell’s equations themselves can acquire physical meaning only after a physical method for measuring the introduced fields is indicated. To date, such a “closing equation” is the equation of motion of charged particles under the action of the Lorentz force. Recall that at different time periods as an electromagnetic force, the Lorentz force was not the only one. Among the most famous expressions were: Ampère’s force, Weber’s force and some others. If modern electrodynamics had a self-consistent nature, then, since the fields manifest themselves by their force action, the expression for the electromagnetic force would have to be derived from Maxwell’s equations rather than being introduced artificially. Such an expression was obtained in [17] and it differs from the expression for the Lorentz force. Can the expression for the Lorentz force be regarded as fundamentally strict and consistent as an electromagnetic force? Apparently not! Although the achievements of modern electrodynamics are well known, it is necessary to note some controversial points. First, even in modern electrodynamics, deceleration by radiation is additionally introduced, which, however, leads to a senseless spontaneous acceleration of charges (that is only postulatively limited by imposing conditions on the field values). Secondly, the very appearance of quantum mechanics suggests that the Lorentz force does not adequately describe the behavior of charges on atomic scales. Thirdly, for the known particle drift phenomenon, it is somewhat strange that its velocity 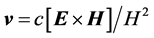 is independent of the charge, mass, and field values themselves, but depends only on the ratio of the fields
is independent of the charge, mass, and field values themselves, but depends only on the ratio of the fields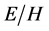 . Thus, the system of differential equations of modern electrodynamics cannot be regarded as fundamentally strict and completely self-consistent, capable of imposing restrictions on other branches of physics.
. Thus, the system of differential equations of modern electrodynamics cannot be regarded as fundamentally strict and completely self-consistent, capable of imposing restrictions on other branches of physics.
Further, Maxwell’s equations are obtained by phenomenological generalization of experimental facts at low velocities (by analogy with hydrodynamics). Therefore, do not expect that they are guessed in the final form. Maxwell’s equations (or the wave equation) determine the phase velocity, while the relativity theory has a “claim” to the maximum speed of signal transmission―the group velocity. In fact, we always deal with a specific light, so this fact should be marked by some index: for example, instead of c we need to write a parametric dependence 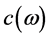 and the wave equation will be an equation for the Fourier harmonic. The requirement of the invariance of the Maxwell equations relative to the coordinate and time transformations is groundless, since the fields and equations for them can be introduced in a variety of ways, provided that the measured effects of these fields correspond to the values actually observed in the experiments. For example, in [18] it was shown that there exist non-local field transformations that preserve Maxwell’s equations with invariant time. It was shown in [19] that nonlinear and nonlocal transformations can be introduced so that for certain field transformations the field equations are invariant with respect to the Galilean transformations.
and the wave equation will be an equation for the Fourier harmonic. The requirement of the invariance of the Maxwell equations relative to the coordinate and time transformations is groundless, since the fields and equations for them can be introduced in a variety of ways, provided that the measured effects of these fields correspond to the values actually observed in the experiments. For example, in [18] it was shown that there exist non-local field transformations that preserve Maxwell’s equations with invariant time. It was shown in [19] that nonlinear and nonlocal transformations can be introduced so that for certain field transformations the field equations are invariant with respect to the Galilean transformations.
4. Michelson-Morley Experiment
Below, we will analyze what should be obtained in the experiments of Michelson-Morley and others from the position of the principle of relativity [20] [21] . It is known that light manifests itself in various phenomena either as a particle or as a wave. First we assume the corpuscular nature of light. Then the Michelson-Morley interferometer model can be represented as two arms with one ideal reflector in the center of the installation and two reflectors at the ends of the arms (Figure 1).
Let two particles moving parallel to each other with velocity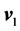 , fall into the given installation, which itself moves with a velocity
, fall into the given installation, which itself moves with a velocity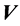 , with
, with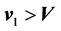 . Then at
. Then at
![]()
Figure 1. Corpuscular model of the Michelson experiment.
point O1 the particle velocity relative to the installation will be . After reflection in the center of the installation, the particle 1 will move in a perpendicular direction with the same (in modulus) velocity
. After reflection in the center of the installation, the particle 1 will move in a perpendicular direction with the same (in modulus) velocity ![]() relative to the installation. Particles will be reflected from the ends of the arms simultaneously. Also, the particles are reached simultaneously both point O and point O1. No difference in the velocities of these two particles for two mutually perpendicular directions will be observed, regardless of the velocities
relative to the installation. Particles will be reflected from the ends of the arms simultaneously. Also, the particles are reached simultaneously both point O and point O1. No difference in the velocities of these two particles for two mutually perpendicular directions will be observed, regardless of the velocities![]() ,
,![]() . Thus, if we consider light as a particle flux, then the experiments of Michelson-Morley (of Kennedy- Thorndike, Tomaschek, Bonch-Bruevich and Molchanov, and others) could not yield any positive result.
. Thus, if we consider light as a particle flux, then the experiments of Michelson-Morley (of Kennedy- Thorndike, Tomaschek, Bonch-Bruevich and Molchanov, and others) could not yield any positive result.
Let us now assume the wave nature of light. In this case, the speed of light can depend only on the properties of the medium and the internal characteristics of the propagating light itself. We will consider the etheric concept below, but for now we will rely only on the classical principle of relativity in a vacuum. If the light is a wave, then the speed of the source changes only the frequency. Thus, for a given frequency ω, the speed of light ![]() does not depend on the velocity of the source. Here we mean the following: light waves of one frequency are identical to each other. And if we perceive the light of frequency ω, it is completely indifferent whether it was radiated by the source at the same frequency or was radiated with frequency
does not depend on the velocity of the source. Here we mean the following: light waves of one frequency are identical to each other. And if we perceive the light of frequency ω, it is completely indifferent whether it was radiated by the source at the same frequency or was radiated with frequency![]() , but the frequency changed due to the motion of the source
, but the frequency changed due to the motion of the source ![]() (due to the Doppler effect). In both cases, the measured value of
(due to the Doppler effect). In both cases, the measured value of ![]() will be the same. Let us now return to the experiments of Michelson-Morley and others. Since the incident light, the light transmitted by the thin plate, and the light reflected from the mirrors have the same frequency in one and the same observation system, the speed of light
will be the same. Let us now return to the experiments of Michelson-Morley and others. Since the incident light, the light transmitted by the thin plate, and the light reflected from the mirrors have the same frequency in one and the same observation system, the speed of light ![]() remained constant for two perpendicular directions and experiments could not detect anything.
remained constant for two perpendicular directions and experiments could not detect anything.
The Towson experiment with two identical lasers also could not detect anything, since when the beams are brought into a single picture (in one direction) the frequencies become the same, and no regular beats will be observed. Thus, an attempt to seek changes in the speed of light in experiments with one fixed frequency is incorrect in its essence. The only dependence you can try to detect is![]() : all other dependencies can only enter indirectly, through the Doppler effect.
: all other dependencies can only enter indirectly, through the Doppler effect.
The Kennedy-Thorndike interferometer differed from Michelson’s interferometer only in that a different length of perpendicular arms was chosen at once. However, for an interference pattern, only the difference in the path of the rays relative to the wavelength of the light used (a fraction of the wavelength) is important. In addition, the accuracy of measuring the lengths of the interferometer arms (for example, the Michelson interferometer) is always less than the wavelength of the light used. Consequently, contrary to the opinion of [7] , the Kennedy-Thorndike experiment is fundamentally no different from the Michelson-Morley experiment.
The conclusion is the following: even if the result of this experiment were zero, it would not be able to distinguish Galilean invariance from Lorentz invariance. The Michelson-Morley experiment does not support the constancy of the light speed and does not disprove any classical principles. The installations with a fixed position of the source and receiver relative to a fixed installation moving as a whole in the medium are not capable to detect a change in the interference pattern (in-phase superposition of waves) with a change in orientation (rotation) of the installation. Thus, if the principle of relativity is true (even in the Galilean form!), then the result of the Michelson-Morley experiments (and also of Kennedy-Thorndike, Tomaschek, Bonch-Bruevich and Molchanov, etc.) must be strictly zero in the absence of ether under any assumptions!
If we accept the hypothesis of the existence of ether, then the speed of light will depend on the properties of this medium. Just like for sound, it does not depend on the speed of the source, but it is added up with the speed of the receiver (the buzz from the supersonic airplane is propagated at a constant speed, fixed by the medium and, as a result, the airplane is ahead of the sound). It is obvious that since light interacts both with matter (is scattered or absorbed), and with ether (propagates in it), then the interaction of ether with matter must be observed. But the relativistic interpretation of the Michelson-Morley experiment presupposed something incredible: the rigid “binding” of light to the ether, together with the total absence of interaction of the ether with the bodies (without the entrainment by the Earth, the installation). Naturally, in the case of partial entrainment of the ether, the theory becomes more complicated. However, this does not refute the ether hypothesis. Relativists also propose to act as in a joke about a drunkard under the lamp: seek not where he can find, but where it’s easier to seek.
We will not discuss experiments in which intensity was compared (this is the same as comparing average temperatures for two hospitals, including morgues), but make some remarks concerning the initial idea of interference experiment from the viewpoint of ether concepts. In fairness, it should be noted that the Michelson experiment and its analogs (despite the disputes on the installation device and the theory) always confidently gave a non-zero velocity of the ether wind taking into account possible errors [22] [23] . Marinov [24] [25] , Silvertus [26] found the correct speed relative to the relic radiation. Only when shielding with a metal casing [27] , the results turned out to be practically zero (at the present time all devices are made a locally closed system). And, for example, the local speed of sound in the cabin of the aircraft will remain constant (independent of the external wind), even with supersonic movement of the aircraft. The etheric viewpoint does not contradict the results obtained: Fresnel entrainment for metal bodies is total, and therefore the ether is at rest relative to the device (locally) inside the metal casing and searching the ethereal wind inside is meaningless.
Another point is usually hushed up. The whole set of experimental data on optics testifies to the correctness of the Huygens principle: every point to which the wave has reached is a source of secondary waves. Even in the absence of metallic screening, a thin plate of glass (or air) is sufficient for necessity to take into account the reemission of light by these locally resting elements. As a result, the actually measured speed in the ether concept should be obviously less than the speed of the Earth’s motion.
Thus, the Michelson-Morley experiment does not confirm the strict Lorentz invariance of the speed of light.
5. The Speed of Light and Addition of Velocities
To begin with, it is necessary to determine what is meant by the speed of such an “object” as light. After all, in the experiments one talked about small variations against a background of enormous magnitude. Of course, the classical definition of speed, as the ratio of the traversed path to the elapsed time interval![]() , is methodically preferable, because this definition does not completely distort the “object” in the process of its movement. But the determination of the light speed through the product of the wavelength at the frequency
, is methodically preferable, because this definition does not completely distort the “object” in the process of its movement. But the determination of the light speed through the product of the wavelength at the frequency ![]() immediately raises several questions. First, we do not directly see the process of electromagnetic oscillations itself (in contrast to mechanical oscillations). Consequently, we cannot be absolutely sure whether the “object” itself has wave properties, or wave properties are only manifested (are generated) in the process of its interaction with the measuring instrument. Secondly, the speed calculated in the second way is the speed of some wave process inside our measuring device. Consequently, it is still necessary to prove that the speed of movement of our “object” (of light) outside the device coincides with this calculated speed inside the device (in other medium!). There are no exhaustive proofs, as we see it.
immediately raises several questions. First, we do not directly see the process of electromagnetic oscillations itself (in contrast to mechanical oscillations). Consequently, we cannot be absolutely sure whether the “object” itself has wave properties, or wave properties are only manifested (are generated) in the process of its interaction with the measuring instrument. Secondly, the speed calculated in the second way is the speed of some wave process inside our measuring device. Consequently, it is still necessary to prove that the speed of movement of our “object” (of light) outside the device coincides with this calculated speed inside the device (in other medium!). There are no exhaustive proofs, as we see it.
However, in any case, the result is at least unambiguous, since the concept of speed in classical physics is clearly defined. And only in relativistic physics there are many “passports” for the “mysterious agent 007”-for light. Let us list them: 1) the “Great constant” c, to which is given a relativistic oath, 2) the coordinate velocity, when the relativists even cannot hide the need for sacrilegious![]() , 3) the phase velocity by which geodesists work [28] , opticians calculate microscopes and telescopes, astronomers calculate refraction, 4) the group speed, which was regretfully introduced by Rayleigh and which is rarely used by practitioners. But relativists often declare the latter to be real, if it does not accidentally turn out to be negative or more than the constant c assigned by them. The explicit “train station cheating with three glasses”: guessed―did not guess.
, 3) the phase velocity by which geodesists work [28] , opticians calculate microscopes and telescopes, astronomers calculate refraction, 4) the group speed, which was regretfully introduced by Rayleigh and which is rarely used by practitioners. But relativists often declare the latter to be real, if it does not accidentally turn out to be negative or more than the constant c assigned by them. The explicit “train station cheating with three glasses”: guessed―did not guess.
In the course of general physics, the relativistic law for velocity addition is usually considered in the one-dimensional case (the formula of the velocity addition was published by Larmor in “Aether and Matter” in 1900, before the creation of SRT).
Consider the following methodological remark [21] [29] . One rather strange fact from the SRT is the non-commutativity of the relativistic law for velocity addition of non-collinear vectors. The property of non-commutativity and the fact, that the Lorentz transformations without rotations do not compose a group, are mentioned in some theoretical physics textbooks. By contrast, a similar property in quantum mechanics essentially changes the entire mathematical formalism and physically expresses a simultaneous immeasurability of non- commutating values. What fundamentally changed in the latter case? We see from the general relativistic law for velocity addition that the final velocity
![]()
where ![]() and
and ![]() are the velocities of the first and second bodies accordingly. Clearly, the result depends on the order of transformation. In such a case, what can the decomposition of the velocity vector into components mean?
are the velocities of the first and second bodies accordingly. Clearly, the result depends on the order of transformation. In such a case, what can the decomposition of the velocity vector into components mean?
The classical law for velocity addition relates only to the translational motion of bodies. If there is also an oscillatory motion, then in general terms nothing definite about the total velocity can be said even for nonrelativistic velocities. For example, the velocity of a malleus blow to a tuning fork has no relation to the velocity of propagating waves.
Although the question of the speed of light was stated above, we formulate more clearly the law of velocity addition for a light signal (for a purely corpuscular and purely wave model of light) using the example of one-dimensional motion. The axis is directed from the source to the receiver. Suppose, at a distance L from the receiver, the source emits a light beam of some frequency![]() . Then two situations are possible. 1) Regardless of the nature of light, when the receiver moves at a speed v with respect to the source, the signal acquisition rate
. Then two situations are possible. 1) Regardless of the nature of light, when the receiver moves at a speed v with respect to the source, the signal acquisition rate ![]() will be determined by the geometric sum
will be determined by the geometric sum![]() , and the frequency of the perceived light will be determined by the simplest classical Doppler law
, and the frequency of the perceived light will be determined by the simplest classical Doppler law![]() . It is completely different the question of which local speed (when all measurements are conducted inside a receiver of fixed dimensions) will be registered by the receiver: this value may depend on device of the receiver, frequency
. It is completely different the question of which local speed (when all measurements are conducted inside a receiver of fixed dimensions) will be registered by the receiver: this value may depend on device of the receiver, frequency![]() , on the nature of the light (whether it is wave, or point particle, or particle with internal degrees of freedom) etc. 2) When the source of a signal moves with a speed v, the result depends on the nature of the light. If the light is a stream of particles, then again we obtain the linear classical law for velocity addition
, on the nature of the light (whether it is wave, or point particle, or particle with internal degrees of freedom) etc. 2) When the source of a signal moves with a speed v, the result depends on the nature of the light. If the light is a stream of particles, then again we obtain the linear classical law for velocity addition![]() . In the case that light is a wave, we are actually dealing with the addition of translational and oscillatory motion and the theorist cannot explicitly write the dependence
. In the case that light is a wave, we are actually dealing with the addition of translational and oscillatory motion and the theorist cannot explicitly write the dependence ![]() and Doppler’s law. In principle, a relationship with characteristics of the “medium” can be found for the value of the velocity. We recall that the speed of sound in gases can be expressed in terms of the following quantities: the molecular weight of the gas, the temperature, the adiabatic exponent. For solids the longitudinal and lateral velocity of sound is expressed in terms of density, Young’s modulus and Poisson’s ratio. For fluids one needs knowledge of certain empirical coefficients. Regarding frequency: only in the limit of small oscillations frequency is determined from the law of Doppler
and Doppler’s law. In principle, a relationship with characteristics of the “medium” can be found for the value of the velocity. We recall that the speed of sound in gases can be expressed in terms of the following quantities: the molecular weight of the gas, the temperature, the adiabatic exponent. For solids the longitudinal and lateral velocity of sound is expressed in terms of density, Young’s modulus and Poisson’s ratio. For fluids one needs knowledge of certain empirical coefficients. Regarding frequency: only in the limit of small oscillations frequency is determined from the law of Doppler![]() . All dependencies can be significantly complicated in the case of arbitrary distances, directions of motion, arbitrary fields and the possible presence of ether for different models of light. Thus, in general case both the definition of the law for velocity addition and the speed of light itself (again―not local, inside the receiver, but in a vacuum between the source and receiver!) together with the Doppler law is the prerogative of experience.
. All dependencies can be significantly complicated in the case of arbitrary distances, directions of motion, arbitrary fields and the possible presence of ether for different models of light. Thus, in general case both the definition of the law for velocity addition and the speed of light itself (again―not local, inside the receiver, but in a vacuum between the source and receiver!) together with the Doppler law is the prerogative of experience.
Let us make one remark about the “extraordinariness” of the relativistic law for velocity addition, which allows us to exchange a light signal, even when the algebraic sum of the velocities is greater than c. Let’s pay attention to the obvious fact: signals for information exchange should be sent necessarily in the direction of the object, and not in the opposite direction. Therefore, there is nothing surprising in the exchange of signals in the classical case also, when, as a result of the formal addition of velocities, ![]() is found. Let two aircrafts take off from the aerodrome O at speeds of
is found. Let two aircrafts take off from the aerodrome O at speeds of ![]() and fly apart from each other in opposite directions of the X axis (that is, at the relative speed of
and fly apart from each other in opposite directions of the X axis (that is, at the relative speed of![]() ). Is it possible to exchange sound signals between them? Of course! Since the sound wave propagates in the air regardless of the speed of the source
). Is it possible to exchange sound signals between them? Of course! Since the sound wave propagates in the air regardless of the speed of the source ![]() at the time of signal emission, the first aircraft (sending the signal) will catch up with the wave front propagating in the positive direction of the X axis, but the second aircraft will “compete” with the wave front propagating in the negative Direction of the X axis. Both aircraft are moving slower than the corresponding sections of the nearest wave front (see Figure 2).
at the time of signal emission, the first aircraft (sending the signal) will catch up with the wave front propagating in the positive direction of the X axis, but the second aircraft will “compete” with the wave front propagating in the negative Direction of the X axis. Both aircraft are moving slower than the corresponding sections of the nearest wave front (see Figure 2).
![]()
Figure 2. Exchange of sound signals between flying airplanes.
It is also obvious that the physical limitation on the speed cannot be imposed by mathematics (the fact that under the radical sign there will be a negative value in some expressions). We just need to remember that all the SRT formulas were obtained using the exchange of light signals (Einstein’s synchronization method). If the body moves at once faster than light, it simply cannot be caught up with the signal sent after it. Similarly, you can introduce the synchronization with the help of sound (and there will also be singularities in the formulas), but this will not be followed by the impossibility of supersonic speeds. The speed of propaga- tion of disturbances (sound or light) in a medium is in no way connected with the speed of movement of some body through this medium.
Note the curious facts. The speed of light is deliberately chosen in SRT as the maximum speed (as an insuperable boundary). The relativistic law for velocity addition is arranged so that the total velocity is always obtained no more than the speed of light, i.e. it would be impossible “to jump into the light train”. In this case, if one of the speeds is chosen equal to c, then the final speed will also be equal to c, regardless of the direction of the second speed. That is, it would also be impossible to jump off the light train. The speed of not only light, but also of the object would always remain equal to c. However, if for the mythical world of tachyons we deliberately choose velocities greater than the speed of light, then we will still get a value less than the speed of light. At the same time, you can get exactly the same final speed even if you add two speeds, each of which is less than the speed of light:
![]()
For example, the relativistic addition of two motions with velocities ![]() gives the final speed
gives the final speed![]() , as well as the addition of two motions with velocities
, as well as the addition of two motions with velocities![]() . Thus, there is ambiguity: do we observe some particle formed during the sub-light decay of a real particle from our world, or we see a superluminal decay of mythical tachyons that would seem to be impossible to see. It is also strange that it would not be possible to launch a superluminal probe from a superluminal rocket ahead in the direction of motion―it would have struck the missile’s body, flying with the sub-light speed back (relative to the rocket).
. Thus, there is ambiguity: do we observe some particle formed during the sub-light decay of a real particle from our world, or we see a superluminal decay of mythical tachyons that would seem to be impossible to see. It is also strange that it would not be possible to launch a superluminal probe from a superluminal rocket ahead in the direction of motion―it would have struck the missile’s body, flying with the sub-light speed back (relative to the rocket).
Generally speaking, the intrinsically contradictory properties of light in the SRT are simply postulated. Therefore, Fock’s assertion [30] that light is a simpler phenomenon than a ruler is unfounded. In fact, the SRT uses the speed of light as one of the standards. Recall that in classical kinematics there are two standards: length and time. We “formulate” the obvious “laws of constancy of standards”: the length of the standard of 1 m is constant and equals to one meter, the duration of the standard of 1 sec is constant and equals to one second, but all ears were buzzed about “the Great Law of the Constancy of the relativistic standard”! Since the introduction of a standard is some definition, its properties are not subject to discussion [4] . As a result, everything related to the light propagation ceases to be the prerogative of experience in the SRT. And since all calculations in the SRT are written only for events―flashes of light, then the SRT is logically inconsistent (not to mention that the use of the properties of light in a vacuum unfoundedly extended to all other “non-vacuum” phenomena).
One more remark concerns experimental results. The dispersion of data in each of the experiments on measuring the light speed is usually high. And the small variations declared in the SRT are obtained only after a certain statistical processing, that is, after fitting to the desired results. This already led to confusions: the declared most probable value of the light speed was changed twice with explicit yields beyond the declared tolerances (see [31] ). Note that in space, the dispersion of light was discovered long ago [32] . One can give an example when the emission lines appeared 2 months after the detection of the X-ray flare [33] , which can also be related to the dispersion of light in a vacuum.
Even for a vacuum, the light speed can depend on the frequency. It is generally accepted that when particles are injected into a vacuum, various processes occur in it, such as the appearance of virtual particle-antiparticle pairs. Many interaction processes can be described using virtual pairs. In the course of light propagation, it also affects the properties of the vacuum; in particular, vacuum polarization can take place. Consequently, the reciprocal effect of a polarized vacuum on the process of light propagation must exist according to the reciprocity principle. As a result, light of a certain frequency will propagate through the vacuum―some “medium” with a certain permeability ε, determined by the propagating light itself, that is,![]() .
.
There are various methods for measuring the speed of light, for example: astronomical methods, interrupt method, rotating mirror method, radio geodetic method, standing wave method (resonator), method of independent measurements ofλ and ν. Currently, the latter method is the most accurate; it is this method that the Bureau of Standards measures the speed of light to within an eighth sign of accuracy. However, in this way there are fundamental difficulties [13] . Besides, it should be noted that this method is fundamentally limited: it can be connected either to the local (within the device) speed of light, or may not have absolutely no relation to the speed of light, if the light is not a pure wave at all.
6. Analysis of Pseudo-Proofs for Existence of Invariant Light Speed
When using the interval in the SRT pseudo-proofs, the following moment is not emphasized: a specific light is used, going from one point to another, that is, the substitution of ![]() in the interval must be done. But in such a case the proportionality of intervals (from textbooks) leads to an indeterminate relationship:
in the interval must be done. But in such a case the proportionality of intervals (from textbooks) leads to an indeterminate relationship:
![]()
and even equality of intervals cannot be justified. There is a need to refer to experiment again, since this relationship is associated with some “unknown so far” Doppler law. For example, see article [34] for more details on the Doppler law. Thus, theoretical constructions that emanate only from their own principles are not unambiguous.
Let us consider in detail article [35] . In this paper an attempt is made to derive the relativistic law for velocity addition, but only for parallel velocities, that is, nature is already limited by theory. To begin with, we make preliminary remarks. What can c = constant mean? The velocity of wave propagation does not depend on the velocity of the source in classical physics either. The constancy of the light speed relative to the receiver (not inside the receiver!) has never been confirmed by anyone. Moreover, this constancy was refuted by Rømer in the determination of the magnitude of the light speed on the eclipses of Io―the satellite of Jupiter. Obviously, the time of signal reception depends on the motion of the receiver (otherwise values ![]() would not appear in the formulas at all). And the expression
would not appear in the formulas at all). And the expression ![]() determines only the speed of the wave process inside the closed measuring device, but not the speed of the signal propagation in the surrounding space. Time and clocks are completely different concepts. Synchronization of clocks generally has nothing to do with the course of time and is not necessary at all, since it does not change the duration
determines only the speed of the wave process inside the closed measuring device, but not the speed of the signal propagation in the surrounding space. Time and clocks are completely different concepts. Synchronization of clocks generally has nothing to do with the course of time and is not necessary at all, since it does not change the duration![]() . And a primitive exchange of signals with each other reminds the pigeon post of the Middle Ages. Unlike the course of time, the clock’s progress and their desynchronization depend on the device of these same clocks.
. And a primitive exchange of signals with each other reminds the pigeon post of the Middle Ages. Unlike the course of time, the clock’s progress and their desynchronization depend on the device of these same clocks.
The author [35] set the goal to show that the most general relation (for parallel velocities!), compatible with the principle of relativity, is the law for velocity addition
![]()
How a special case can be the most general thing: is it possible in reality to guarantee a strict parallelism of velocities? Obviously not! For two velocities u and v with given modules, the case of their parallelism is a set of measure zero. And for noncollinear vectors, the result of relativistic addition already depends on the order of its application (on the order of addition of velocities)!
The value of ![]() is not an “invariant velocity”, but a boundary velocity: the addition of two quantities less than this speed gives a value that is also smaller than this speed, but the addition of two quantities larger than this speed also gives a value less than this speed! Only if at least one of the quantities is exactly equal to this boundary speed, the result of “addition” will again be this speed. As you can see, additional groundless postulates have been introduced about the impossibility of achieving velocities, more than
is not an “invariant velocity”, but a boundary velocity: the addition of two quantities less than this speed gives a value that is also smaller than this speed, but the addition of two quantities larger than this speed also gives a value less than this speed! Only if at least one of the quantities is exactly equal to this boundary speed, the result of “addition” will again be this speed. As you can see, additional groundless postulates have been introduced about the impossibility of achieving velocities, more than ![]() and about the existence of a strange boundary speed from which it is impossible to “jump off” and on which it is impossible to “jump”.
and about the existence of a strange boundary speed from which it is impossible to “jump off” and on which it is impossible to “jump”.
Mermin [35] states about the method of reducing the function of two variables to a function of one variable. But this is not always possible in mathematics; therefore, some additional hypotheses and limitations will be artificially introduced, and even through thought experiments! The author of [35] presupposes the fulfillment of the relativity principle, that is, that we are dealing with isolated systems (identical systems without interaction, that is already a limitation of Nature), but it also seeks an open relationship between relative velocities. In expression (2.3) from [35] , he specially introduced other variables, so that the meaning of the previous expression (2.2) became invisible: pay attention to the subscripts! In expression (2.2), the subscripts are clearly joined together: ![]() that corresponds to the physical meaning of the velocity addition. If the author wanted to write an expression for
that corresponds to the physical meaning of the velocity addition. If the author wanted to write an expression for ![]() through a change of sign, then it was necessary to write
through a change of sign, then it was necessary to write![]() . Thus, instead of (2.3), the equality
. Thus, instead of (2.3), the equality ![]() must be written, and no symmetry (2.6) with respect to the arguments follows from any “general considerations”. Moreover, our viewpoint is confirmed by the fact that the general relativistic law for velocity addition depends on the order of the velocities for noncollinear vectors (it is noncommutative!). Therefore, a particular case of parallel velocities does not need to be symmetric (commutative) either.
must be written, and no symmetry (2.6) with respect to the arguments follows from any “general considerations”. Moreover, our viewpoint is confirmed by the fact that the general relativistic law for velocity addition depends on the order of the velocities for noncollinear vectors (it is noncommutative!). Therefore, a particular case of parallel velocities does not need to be symmetric (commutative) either.
We make the following remark. It is necessary to accurately subdivide the measurable velocities (related to the measuring device located in some system) and the calculated velocities (not related to the system in which the measuring instrument is located). Obviously, in our case, the speed ![]() is the calculated speed, because just for this reason some function f is introduced, but the variables of this function-the velocities
is the calculated speed, because just for this reason some function f is introduced, but the variables of this function-the velocities ![]() and
and![]() ―are the measurable velocities. But then the measuring device can only be in system B. Therefore, the addition of a new point D in [35] only leads to the fact that new calculated velocities
―are the measurable velocities. But then the measuring device can only be in system B. Therefore, the addition of a new point D in [35] only leads to the fact that new calculated velocities ![]() were simply introduced in expression (2.7), but the measuring instrument cannot measure them in the system B. In doing this, in the first of the expressions (2.8), the measurable and calculated velocities were mutually replaced, that changes the physical meaning of the seeked computational function. The possibility of interchanges the measurable and calculated quantities in (2.9) is an additional physical hypothesis. We cannot assume in advance that when the measurable and calculated quantities are replaced, the form of the unknown function remains one and the same. For classical physics (linear dependence), the calculated velocity does not really depend on the motion of the observation system, but in relativistic physics for non-collinear vectors this is no longer so.
were simply introduced in expression (2.7), but the measuring instrument cannot measure them in the system B. In doing this, in the first of the expressions (2.8), the measurable and calculated velocities were mutually replaced, that changes the physical meaning of the seeked computational function. The possibility of interchanges the measurable and calculated quantities in (2.9) is an additional physical hypothesis. We cannot assume in advance that when the measurable and calculated quantities are replaced, the form of the unknown function remains one and the same. For classical physics (linear dependence), the calculated velocity does not really depend on the motion of the observation system, but in relativistic physics for non-collinear vectors this is no longer so.
Note that in mathematics there is no such general property that any function of two variables can be expressed as a function of one variable, even if it is “continuous and differentiable”. And the plausible phrases about “parametric dependence”, “fixation of a variable” and the replacement of the partial derivative in (2.10) by the total derivative (2.14) are intended to hide the obvious deception. Each can elementarily find examples when this does not work. Thus, (2.17) does not hold in the general case, to which the “proof” of Mermin allegedly claims. Since we have seen earlier that the symmetry (2.6) does not hold in the SRT, then the equality (2.18) does not work all the more so. Then the expression (2.19) and the search for the function h lose meaning. Also the value ![]() could be equal to infinity if the derivative at zero turns out to be zero.
could be equal to infinity if the derivative at zero turns out to be zero.
Further, instead of (3.1), we must write other self-consistent expressions:
![]()
Expression (3.5) is correct, since it uses only classical relativity. It is obvious that (3.6) no longer corresponds to the previous definitions. But even if you forget about everything, said above, including the absence of meaning in the search for h, then the simplest solution (3.9) will be![]() . Note, firstly, that in any case, it can only be about determining the calculated speeds (so the best choice is the simplest option). But measurable speeds without our games with mathematics are determined from experiments. Secondly, take an attention that Mermin from the expression (3.9) tries to justify a certain unified constant for all cases of life. Note that the tortoise and the hare meet in any case: if one or both from them stand, or move with arbitrary speeds. Choosing u = 0, we again get the simplest choice in the particular case
. Note, firstly, that in any case, it can only be about determining the calculated speeds (so the best choice is the simplest option). But measurable speeds without our games with mathematics are determined from experiments. Secondly, take an attention that Mermin from the expression (3.9) tries to justify a certain unified constant for all cases of life. Note that the tortoise and the hare meet in any case: if one or both from them stand, or move with arbitrary speeds. Choosing u = 0, we again get the simplest choice in the particular case![]() . But the most important thing is that the integration of this fictitious function does not give any law for velocity addition due to non-commutativity.
. But the most important thing is that the integration of this fictitious function does not give any law for velocity addition due to non-commutativity.
If we allow the possibility of exotic (relativistic) transformations from the belief in the relativity principle, that is, assuming a possible dependence of a row of quantities on the relative velocity, then an additional hypothesis is the assumption of the dependence of these quantities on the modulus of the relative velocity. Then we cannot even be sure of the equality of the quantities measured when going back and forth. For example, then you can doubt that in the system of reference of the train![]() . Further, again it is not necessary to confuse the measurable and calculated quantities: instead of (4.1) it is necessary (for consistency with the function f) to check the value
. Further, again it is not necessary to confuse the measurable and calculated quantities: instead of (4.1) it is necessary (for consistency with the function f) to check the value![]() . The author’s ar-
. The author’s ar-
guments relate to the train’s motion system, that is, ![]() (4.3) and, instead of (4.6), we can only write
(4.3) and, instead of (4.6), we can only write![]() .
.
Then the author postulates (this is again an additional hypothesis) that this relation will be preserved in the v-system also. We will not correct all the intermediate formulas of the analyzed article, but directly write the final expression
![]()
and the limit:
![]()
But again, from here no special functions ![]() should follow.
should follow.
Further, the author notes that for a negative value of K, the law for velocity addition (5.2) can lead to the result![]() , if
, if ![]() and
and ![]() . But for some reason the author ignores another strangeness with a positive value of K. The boundary velocity
. But for some reason the author ignores another strangeness with a positive value of K. The boundary velocity ![]() breaks up the phenomena into three strange “Worlds”: I)
breaks up the phenomena into three strange “Worlds”: I)![]() , II) c, III)
, II) c, III)![]() . In this case
. In this case![]() ,
, ![]() ,
, ![]() ,
, ![]() , but with the addition of velocities, each of which is greater than c, the particles “fall” into I “World”:
, but with the addition of velocities, each of which is greater than c, the particles “fall” into I “World”: ![]() (the same result will be for
(the same result will be for![]() ).
).
There is no evidence of the invariance of the light speed in a vacuum. The speed of wave propagation does not depend on the velocity of the source for any waves and at any speed of their propagation (the set among them occurs). This is just a property of wave motion, including in classical physics. The velocity ![]() determines the local velocity of wave propagation inside the measuring device. And determination of the value of c on the eclipses of the Io―the satellite of Jupiter, speaks of the dependence of the light speed on the speed of the receiver. In any case, there is no other evidence.
determines the local velocity of wave propagation inside the measuring device. And determination of the value of c on the eclipses of the Io―the satellite of Jupiter, speaks of the dependence of the light speed on the speed of the receiver. In any case, there is no other evidence.
Mermin proposes to determine the value of K from expression (5.3), forgetting that in the system B only two velocities are measurable: ![]() and
and![]() . In essence, the expression (5.3) is a definition for the not measurable value of velocity
. In essence, the expression (5.3) is a definition for the not measurable value of velocity ![]() in the system B. But one expression cannot simultaneously determine two unknown quantities:
in the system B. But one expression cannot simultaneously determine two unknown quantities: ![]() and K. The author suggests to “ask” about the value
and K. The author suggests to “ask” about the value ![]() in the system A. Relativity turns strange! For some reason, we cannot believe the observer in system A that he knows about the lengths and times that we do not measure in his system (this is unprofitable from the relativistic viewpoint). We ostensibly must calculate these lengths and times by the artificial relativistic rules. But we must blindly believe in the observer’s testimony from the system A about velocities. In general, “here we read, here we do not read” ... and as it is sang in the song “And the rest, beautiful marquise All right, all right” (the SRT must be defended at any cost?)!
in the system A. Relativity turns strange! For some reason, we cannot believe the observer in system A that he knows about the lengths and times that we do not measure in his system (this is unprofitable from the relativistic viewpoint). We ostensibly must calculate these lengths and times by the artificial relativistic rules. But we must blindly believe in the observer’s testimony from the system A about velocities. In general, “here we read, here we do not read” ... and as it is sang in the song “And the rest, beautiful marquise All right, all right” (the SRT must be defended at any cost?)!
Generally speaking, the synchronization method using an infinitely remote source on the median perpendicular to the motion line [21] unambiguously leads to all classical quantities (spatial, temporal and motion characteristics).
We also give brief remarks to the “justification” of the relativistic law for velocity addition in [36] . The requirement that the inverse transformation to a linear transformation and the product of transformations preserve the corresponding structure (constitute a group) are additional requirements (and for noncollinear motions are not satisfied in the SRT). When Terletskii claims about the homogeneity of space, but at the same time tries to artificially introduce some strange transformations, it would be worthwhile first to answer the question of what to expect from parallel transformations for such a fictitious “physics” (how to avoid paradoxes). In his expression (7.6) the constant can depend on other coordinates:![]() . The form of the transformation (7.7) itself is a hypothesis: if we talk about generalization, then there may be cross-dependencies of coordinates.
. The form of the transformation (7.7) itself is a hypothesis: if we talk about generalization, then there may be cross-dependencies of coordinates.
Further, the replacement only ![]() changes the orientation of the triple of basis vectors. Consequently, to have changed the nothing in the transformation formulas (as the author wishes), it is necessary to swap
changes the orientation of the triple of basis vectors. Consequently, to have changed the nothing in the transformation formulas (as the author wishes), it is necessary to swap ![]() (this is immediately noticeable for a non-spherical object). The coincidence of the form of direct and inverse transformations remains in question. Large problems with “group properties” arise in the transition to non-collinear vectors, so that all these mathematical exercises look artificial.
(this is immediately noticeable for a non-spherical object). The coincidence of the form of direct and inverse transformations remains in question. Large problems with “group properties” arise in the transition to non-collinear vectors, so that all these mathematical exercises look artificial.
Finally, the dependence of mass on speed is fantasized: not the mass grows at a speed, but the effective force decreases as the speed of the body approaches the transfer rate of the interactions (to the momentum transfer rate)! In classical physics, there is also a similar decrease in effective force.
Thus, the paper [36] also cannot be considered rigorous in terms of justifying relativistic invariance and the law for velocity addition.
7. Conclusions
The principle of relativity and a mathematical skew, with an exaggeration of the role of invariance in physical research, were discussed in the paper. It was analyzed in detail a “bloated soap bubble” with the invariance of the Maxwell equations. Further, the Michelson-Morley experiment was analyzed in terms of various theoretical expectations. This experiment cannot distinguish between Galilean and Lorentz invariance. The fundamental problems associated with the speed of light and with the law for velocity addition were discussed. Some pseudo- proofs of the necessity of the invariant velocity existence are critically examined.
Thus, there is no strong theoretical evidence for the necessity of the invariant velocity existence, as well as experimental confirmation of this statement, including for light.