General Relativity and the Theory of a Self-Interacting Abelian Gauge Field ()
1. Introduction
Three of the fundamental forces in nature are described by Yang and Mills quantum field gauge theories on flat space-time, the fourth interaction, gravity, being a classical theory involving the dynamics of curved space-time is the exception.
The original theory of general relativity (GR) in terms of the metric tensor of curved space-time has been the subject of alternative formulations by different authors during the last 100 years. Some of these correspond to different versions of Einstein’s theory; others are theories that depart from Einstein’s while at the same time describing the known experimental results. Examples of the first type are: Schrödinger’s affine connection [1] ; Palatini’s metric-affine gravity [2] ; Tetrads local coordinate system [3] ; Tetrad field and a complex connection (loop- space gravity) [4] [5] [6] and Arnowitt, Deser and Misner’s foliation of space-time [7] , among others. A long list of alternative theories to GR can be found in the review paper by Clifton et al. [8] .
This situation is peculiar to GR, since nothing similar occurs with the other theories describing the fundamental interactions of matter. The theory of GR is 100 years old, and has successfully passed all experimental tests, making several predictions that had finally been confirmed. So what could explain the search for either different formulations or alternative theories? A possible reason could be the apparent incompatibility between GR and quantum field theory; another explanation may rest on the fact that GR is not a Yang and Mills gauge theory, while all other fundamental interactions are.
The purpose of this paper is to present classical GR under a new dressing which may disclose new properties of the theory and allow establishing a relationship with the other theories of the fundamental interaction of matter.
Eddington [9] , introduced the idea of representing the metric tensor of a four dimensional curved space-time in terms of ten parameters. In the first part of this paper, the equations of the standard theory of GR using the parametric representation of the metric tensor proposed by Eddington are worked out. In the second part the formalism of a self-interacting abelian gauge field is developed.
2. Parametric Form of Einstein’s Equations.
In the book “The Mathematical Theory of Relativity” [9] , Eddington mentions the possibility of representing the metric tensor of a four-dimensional curved space-time in terms of ten parameters. With this in mind, the equations of the standard theory of GR using the parametric representation of the metric tensor will next be developed.
Let 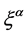 be the coordinates of a 10-dimmensional space with constant metric tensor
be the coordinates of a 10-dimmensional space with constant metric tensor  (
(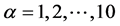 ). The line element in this space is given by:
). The line element in this space is given by:
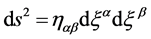 (1)
(1)
A four-dimensional continuum obeying Riemannian geometry can be repre- sented parametrically as a four-dimensional surface in the above mentioned space. Let xi (i = 0, 1, 2, 3) be the parameters on the surface, then the region can be mapped parametrically in terms of  and the line element can be written as:
and the line element can be written as:
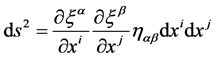 (2)
(2)
and the metric tensor of the curved Σ region is given by:
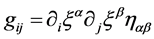 (3)
(3)
The rectangular matrix 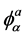 is defined in terms of the inverse metric
is defined in terms of the inverse metric 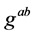 and
and 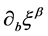 as:
as:
 (4)
(4)
Then  satisfies the relation
satisfies the relation
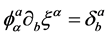 (5)
(5)
The inverse metric tensor can also be written as:
 (6)
(6)
Next, the usual equations of GR are obtained in terms of 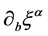 and
and .
.
For the affine connection the normal expression for a torsion-free manifold is used,
 (7)
(7)
Substituting into (7) the expressions given by Equations (3) and (6), and taking into account Equation (5), it follows:
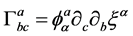 (8)
(8)
In spite of the fact that Equation (8) may look similar to the Weitzenbock connection for a manifold with curvature and torsion, due to the symmetry of the connection, it corresponds to a torsion-free manifold.
By substituting into the usual definition of the Riemann curvature the above expression for the affine connection one gets:
![]() (9)
(9)
and after some straight forward algebraic transformations, making explicit use of the fact that the affine connection is symmetric, we obtain the following expressions for the Riemann and Ricci tensors for a torsion-free curved manifold:
![]() (10)
(10)
![]() (11)
(11)
where it was written![]() , which will be convenient for future reference, and defined
, which will be convenient for future reference, and defined
![]() (12)
(12)
with the following properties:
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
Taking into account that
![]() (17)
(17)
we can re-write (11) as:
![]() (18)
(18)
and taking into account Equation (16) we finally obtain:
![]() (19)
(19)
Equation (19) is the usual Ricci tensor of GR for a torsion-free curved manifold using the parametric representation of the metric tensor.
3. The Self-Interacting Abelian Gauge Theory
Let us consider a set of vectors ![]() labeled by the index
labeled by the index![]() , which runs from 1 to 10 (Latin indices run from 0 to 3), together with a set of vectors
, which runs from 1 to 10 (Latin indices run from 0 to 3), together with a set of vectors ![]() that are defined by the orthonormal condition (sum over α):
that are defined by the orthonormal condition (sum over α):
![]() (20)
(20)
As before, the matrix ![]() is defined by:
is defined by:
![]() (21)
(21)
Next, it is required that the equations for ![]() and
and ![]() be invariant under a local abelian transformation:
be invariant under a local abelian transformation:
![]() (22)
(22)
![]() (23)
(23)
As a consequence of Equation (12) ![]() remains invariant.
remains invariant.
To guarantee the symmetry of the equations one has to introduce a covariant derivative. The standard procedure in normal Yang and Mills theory is to introduce an auxiliary field, the gauge potential![]() , so that the combination
, so that the combination ![]() is covariant. In this paper a new form of covariant derivative is defined by means of what we call a self-interacting abelian gauge. Instead of introducing a new field
is covariant. In this paper a new form of covariant derivative is defined by means of what we call a self-interacting abelian gauge. Instead of introducing a new field![]() , the gauge potential is taken to be the matrix
, the gauge potential is taken to be the matrix![]() , a function of
, a function of ![]() and
and![]() , and the covariant derivative
, and the covariant derivative ![]() is defined as:
is defined as:
![]() (24)
(24)
![]() (25)
(25)
In this form, the gauge potential itself belongs to the group of symmetry. It follows from (16) that ![]() and
and ![]() , as required.
, as required.
Equations (24) and (25) define the covariant derivatives of a self-interacting abelian gauge field. The covariant derivatives can also be written as:
![]() (26)
(26)
As a consequence of (16), the first term on the right hand side in Equation (26) vanishes so that:
![]() (27)
(27)
Similarly,
![]() (28)
(28)
and, since ![]() is invariant:
is invariant:
![]() (29)
(29)
For a given vector![]() , we adopt the convention that
, we adopt the convention that
![]() (30)
(30)
and conversely,
![]() (31)
(31)
where ![]() is any constant matrix and
is any constant matrix and ![]() its inverse.
its inverse.
Under a gauge transformation
![]() (32)
(32)
![]() (33)
(33)
and the covariant derivatives are given by:
![]() (34)
(34)
and
![]() (35)
(35)
These equations, when applied to ![]() and
and![]() , coincide with (24) and (25).
, coincide with (24) and (25).
The idea of self-interacting gauge field can be extended to non-abelian symmetries; nevertheless, the discussion will be restricted here to the abelian case due to its relevance to gravity.
As is the case in any Yang and Mills theory, the commutator of covariant derivatives is proportional to the gauge field![]() .
.
To compute the commutator we first calculate
![]()
from which we obtain:
![]() (36)
(36)
Similarly,
![]() (37)
(37)
Finally,
![]() (38)
(38)
For the special cases in which![]() , the expression for
, the expression for ![]() given in (38) is identical to the Ricci tensor of GR given by Equation (19), as we intended to prove.
given in (38) is identical to the Ricci tensor of GR given by Equation (19), as we intended to prove.
Further,
![]() (39)
(39)
is analogous to Einstein’s equation for the gravitational field. Here κ is the coupling constant and ![]() is a function of the
is a function of the![]() , the energy momentum tensor of matter and external fields, care being taken to rise and lower indices according to the prescriptions given by (30) and (31).
, the energy momentum tensor of matter and external fields, care being taken to rise and lower indices according to the prescriptions given by (30) and (31).
![]() (40)
(40)
It must be emphasized that Equation (38) was derived without any reference to the dynamics of curved space-time. Thus, in this theory space-time can be considered to be a fixed background.
The fact that Equation (39) for the gauge field is identical to the equations of GR implies that the corresponding solutions are the same, thus, for example Schwarzschild solution or the cosmological solutions of GR can correspondingly be looked upon as gauge fields in flat space-time.
4. Conclusion
It has been proved in this work that the equations of an abelian self-interacting gauge field are identical to the parametric form of Einstein’s equations of classical GR for a torsion-free curved space. Therefore, the classical theory of gravity can be describe either by the usual theory of general relativity, based on the dynamics of curved space-time, or, alternatively, as a non-linear self interacting gauge theory. This allows formulating the theory of the gravitational field on an equal footing with the other theories of the fundamental interactions of matter, based on the same general principle: gauge symmetry.
Acknowledgements
The author would like to express his gratitude to the late Samuel Schiminovich for many enlightening discussions.