A Stable and Consistent Document Model Suitable for Asynchronous Cooperative Edition ()
1. Introduction
With the rise of XML technologies and Web services, structured documents have become important tools for the publication and exchange of information bet- ween most often heterogeneous and remote applications. The ever-increasing power of communication networks in terms of throughput and security as well as efficiency is concern, has revolutionized the way of such documents are edited. Indeed, to the classical model of an author editing his document locally and autonomously, was added the (asynchronous) cooperative editing in which, several authors located on geographically distant sites, coordinate to edit asynch- ronously the same structured document (Figure 1).
The central issue addressed in this paper can be simply presented by means of an example of unsynchronized cooperative structured editing process (Figure 1). In fact, one can easily imagine an editing process in which several authors work together to produce a pluri-disciplinary book and such that, according to its own field of expertise, everyone contribute to more or less disjointed parts of the same document.
It may be interesting for these authors to specify previously (may be together) the overall hierarchical structure of the document via a grammatical model; we call thereafter global model of the document. From it are derive for each of the co-authors a dedicated (local) model called thereafter local model. This local model can be regarded as a “view” on the global model and obtained by means of a projection operation performed on it, which retains on the global model only syntactic categories with a demonstrated interest for the considered author.
For example, Figure 1 present an overview of the cooperative edition distributed on three sites. Site 1 is dedicated to the edition and the merging of
![]()
Figure 1. The desynchronized cooperative editing of partial replicas of a structured document.
the (global) document according to the (global) document model G hosted on him. On G, two projections are made to obtain G1 and G2, the local models hosted by site 2 and 3 an used for syntactically constrain the desynchronized edition of the partial replicas of the global document on the sites 2 (resp. site 3). Note that, documents published on these sites can be saved (serialized) then restored by parsing. The overall document is subsequently obtained from the site 1 by performing a consistent expansion3 of the various documents published on sites 2 and 3.
The purpose of this paper is to propose a generic document model allowing to specify syntactically both the global model and derived local models, which are consistent with the global model.
In order to do this, we propose the grammatical structures (a subset of the extended context free grammars) as well as a projection operation which allows to derive from a grammatical structure (global model) and a set of syntactic categories relevant to a given co-author, a local grammatical structure dedicated to him.
Organization of the manuscript: Section 2 presents some concepts and definitions used thereafter. Section 3 presents the grammatical structures, the projection algorithm on grammatical structures and some features of this model. Section 4 is devoted to the conclusion.
2. Preliminaries
2.1. Extended Context Free Grammars, Documents and Compliances
The dependency graph 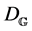 of grammar
of grammar 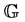 is a graph whose set of node tags is included in
is a graph whose set of node tags is included in  and, for all rules
and, for all rules 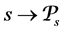 in
in , there is an arrow from
, there is an arrow from  to
to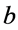 , for all
, for all 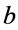 in a word belonging to the language denoted by
in a word belonging to the language denoted by 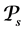 and termed
and termed . An ECFG is said to be non recursive if and only if
. An ECFG is said to be non recursive if and only if ![]() is acyclic, and recursive if not.
is acyclic, and recursive if not.
A document t conforms to a grammar ![]() and we write
and we write![]() , if it is a derivation tree of this grammar: it’s the case if for any t node n labeled
, if it is a derivation tree of this grammar: it’s the case if for any t node n labeled ![]() and with children nodes
and with children nodes ![]() labeled respectively
labeled respectively![]() ,
, ![]() , the word
, the word![]() .
.
2.2. View, Projection, Partial Replica and Consistency
The derivation tree giving a (global) representation of a structured document published cooperatively, makes visible all the grammar’s grammatical symbols. As mentioned in Section 1 above, a coauthor handling such a document using a structured dedicated editor of his area of expertise, do not necessarily have access to all of these grammatical symbols; only a subset of them correspond to syntactic categories perceptible as such by this tool: hence the notion of “view” [4] . A view![]() , is a subset of grammatical symbols (
, is a subset of grammatical symbols (![]() ). Intuitively, they are symbols associated with visible syntactic categories in the considered representation (derivation tree).
). Intuitively, they are symbols associated with visible syntactic categories in the considered representation (derivation tree).
Each view ![]() is associated with a projection operation noted
is associated with a projection operation noted![]() , on derivation trees t which erases nodes labeled by invisible symbols while retaining the subtree structure. Partial replication is the result of the projection of a document (derivation tree) with respect to a given view. For example, in the Figure 2 from the global document t in the center, and views
, on derivation trees t which erases nodes labeled by invisible symbols while retaining the subtree structure. Partial replication is the result of the projection of a document (derivation tree) with respect to a given view. For example, in the Figure 2 from the global document t in the center, and views ![]() and
and ![]() on the alphabet
on the alphabet![]() , we have on the left the partial replica
, we have on the left the partial replica![]() , and on the right the partial replica
, and on the right the partial replica![]() .
.
The edition type considered in this paper is asynchronous. On a site i hosting a document model ![]() on which a partial replica
on which a partial replica ![]() is updated with
is updated with![]() , we will say that
, we will say that ![]() is consistent vis-a-vis a global model
is consistent vis-a-vis a global model![]() , and we write
, and we write ![]() if and only if a document
if and only if a document ![]() exists and
exists and![]() . Also, a local model
. Also, a local model ![]() is consistent vis-a-vis a global model
is consistent vis-a-vis a global model ![]() if and only if
if and only if ![]() such that
such that![]() .
.
2.3. Some Definitions and Notations
Let ![]() be an extended context free grammar,
be an extended context free grammar, ![]() ,
, ![]() ,
, ![]() a view, t a derivation tree for
a view, t a derivation tree for ![]() (
(![]() ),
),![]() the dependency graph of
the dependency graph of ![]() and
and ![]() a production rule.
a production rule.
![]()
Figure 2. One document (center) and two partial replicas obtained by projections.
![]() is said to be finite type if and only if
is said to be finite type if and only if ![]() is non recursive.
is non recursive. ![]() is said to be finite type with respect to
is said to be finite type with respect to ![]() if the restriction of dependency graph
if the restriction of dependency graph ![]() on symbols which belongs to
on symbols which belongs to ![]() is not recursive.
is not recursive.
We note ![]() the t’s set nodes labels, and
the t’s set nodes labels, and ![]() the t’s root node label.
the t’s root node label.
The notation “![]() ” means that “p has the form
” means that “p has the form![]() ”. We introduce function
”. We introduce function ![]() (resp.
(resp.![]() ) which returns the symbol (resp. the symbols) in left hand side (resp. right hand side) of his argument p, a production rule. For example, if
) which returns the symbol (resp. the symbols) in left hand side (resp. right hand side) of his argument p, a production rule. For example, if![]() ,
, ![]() (resp.
(resp.![]() ). Also,
). Also, ![]() means the substitution in the right hand side of p of all occurrences of each symbols
means the substitution in the right hand side of p of all occurrences of each symbols ![]() by the corresponding
by the corresponding![]() . For example, with
. For example, with![]() ,
, ![]() ,
,![]() .
.
![]() is the language generated by grammar
is the language generated by grammar ![]() from symbol
from symbol![]() .
.
3. A Document Model Stable by Projection Operation, for Cooperative Asynchronous Edition
In this section, we present grammatical structures which are a particular form of non-recursive extended context free grammars (ECFG). Indeed, to make the projection (defined below, Section 3.2) possible, it is not permitted to have in this model, recursive grammar symbols5. The grammatical structures will then be models for documents of bounded depths (consequence of the non- recursivity of the symbols) but of unbounded widths. Moreover, they will allow to specify in a homogeneous way both the global model for the global document and the local models for its various partial replicas.
A grammatical structure ![]() is given as:
is given as:
・ a set ![]() of non recursive grammatical symbols, and
of non recursive grammatical symbols, and
・ a set ![]() of production rules. Each rule in
of production rules. Each rule in ![]() has one of the two forms:
has one of the two forms:
- ![]() (classical form of context free grammars rules),
(classical form of context free grammars rules),
- ![]() (i.e.
(i.e. ![]() is build up by a list of
is build up by a list of![]() )
)
We recall that an equivalent ECFG can be evidently be derived from a grammatical structure.
3.2. Projection of a Grammatical Structure
Let ![]() be a grammatical structure,
be a grammatical structure, ![]() a view; let also
a view; let also ![]() be the complementary of
be the complementary of ![]() in
in![]() . The view
. The view ![]() projection on
projection on![]() , termed
, termed ![]() is the grammatical structure
is the grammatical structure ![]() where:
where:
・ ![]() is obtained from
is obtained from ![]() by successive rewriting of symbols in
by successive rewriting of symbols in ![]() in terms of those in
in terms of those in![]() , then, by substituting properly the result (of this rewriting) in the subset of rules
, then, by substituting properly the result (of this rewriting) in the subset of rules ![]() having symbols in
having symbols in ![]() on the left hand side:
on the left hand side: ![]() or
or![]() .
.
![]()
6For example a form of rule like ![]() can be obtained after successive rewriting of a rule; this is not an acceptable form of rule. So a new restructuring symbol
can be obtained after successive rewriting of a rule; this is not an acceptable form of rule. So a new restructuring symbol ![]() is created and rule p is decompose in two new rules as follow
is created and rule p is decompose in two new rules as follow ![]() and
and![]() .
.
・ ![]() : syntactic categories of the projected grammar contains symbols of the view with enventually new symbols introduce for structuring purpose belonging to set
: syntactic categories of the projected grammar contains symbols of the view with enventually new symbols introduce for structuring purpose belonging to set![]() . As the process of obtaining the production rules of the projected model proceed by successive rewriting of symbols which did not belong to the view, it can occur during the rewriting process of some symbols that, new symbols being added for format purpose (or decomposition) in order to bring some rules back to the form of the production rules adopted for the grammatical structures6 (cf. Section 3.1).
. As the process of obtaining the production rules of the projected model proceed by successive rewriting of symbols which did not belong to the view, it can occur during the rewriting process of some symbols that, new symbols being added for format purpose (or decomposition) in order to bring some rules back to the form of the production rules adopted for the grammatical structures6 (cf. Section 3.1).
The algorithm for deriving ![]() and
and ![]() proceeds in two steps:
proceeds in two steps:
Step 1: consider the subset ![]() of
of![]() ’s rules which left hand side does not belongs to the view
’s rules which left hand side does not belongs to the view ![]() and transform
and transform
them by successive rewriting to rules like![]() , an acceptable rule of grammatical structure, with
, an acceptable rule of grammatical structure, with![]() , and
, and ![]() containing only
containing only ![]() symbols. Hence
symbols. Hence ![]() set is given as:
set is given as:
![]() (1)
(1)
Indeed, ![]() can be considered as production rules of a concrete context free grammar
can be considered as production rules of a concrete context free grammar ![]() with
with ![]() as non terminal symbols and
as non terminal symbols and ![]() as terminal symbols; then
as terminal symbols; then![]() .
.
From Equation (1), one easily deduces that ![]() is in fact the union of the rewriting of the productions of
is in fact the union of the rewriting of the productions of ![]() having a symbol belonging to
having a symbol belonging to ![]() in her left hand side. Thus, for every symbol
in her left hand side. Thus, for every symbol ![]() belonging to
belonging to![]() , if we note
, if we note ![]() the set obtained by rewriting rules of
the set obtained by rewriting rules of ![]() having
having ![]() as left hand side, we have
as left hand side, we have ![]() with
with![]() . Recall that, symbols in
. Recall that, symbols in ![]() are considered as terminal symbols when rewriting.
are considered as terminal symbols when rewriting.
Algorithm 1 describes the construction process of![]() . Let’s emphasis that, for effective construction of
. Let’s emphasis that, for effective construction of![]() , the different
, the different
![]()
Algorithm 1. Construction of![]() .
.
sets ![]() should be built according to the topological sorting of the
should be built according to the topological sorting of the ![]() dependency graph: a symbol is evaluated after evaluation of symbols from which it depends.
dependency graph: a symbol is evaluated after evaluation of symbols from which it depends.
![]()
7Note that![]() .
.
Step 2: Consider the subset ![]() of
of![]() ’s rules, with view symbols in left hand side (
’s rules, with view symbols in left hand side (![]() 7); for every rule in this set, replace all occurrences of
7); for every rule in this set, replace all occurrences of ![]() elements in right hand side, by their right hand side counterpart in
elements in right hand side, by their right hand side counterpart in![]() , this by all means; we finally obtain the set
, this by all means; we finally obtain the set ![]() of production rules of the projected grammatical structure.
of production rules of the projected grammatical structure.
![]() (2)
(2)
As for ![]() (Equation (1)), we deduce from Equation (2) that
(Equation (1)), we deduce from Equation (2) that ![]() is the reunion of the sets obtained by rewriting the productions of
is the reunion of the sets obtained by rewriting the productions of ![]() having symbols
having symbols ![]() belonging to
belonging to ![]() in their left hand side, by using
in their left hand side, by using![]() ; that sets is denoted
; that sets is denoted![]() . Thus,
. Thus, ![]() with
with![]() . The construction of
. The construction of ![]() is described in Algorithm 2 below.
is described in Algorithm 2 below.
Algorithm 3 purpose is to construct![]() . It explicitly presents when restructuring symbols are created (line 5) and when they are explicitly used (line 5 and line 8) in generated productions rules.
. It explicitly presents when restructuring symbols are created (line 5) and when they are explicitly used (line 5 and line 8) in generated productions rules.
3.3. Grammatical Structures Properties
Let ![]() be a grammatical structure, and
be a grammatical structure, and ![]() a view;
a view; ![]() satisfies properties below:
satisfies properties below:
Property 1: ![]() is a grammatical structure (stability property); this property is guaranteed by Algorithm 3.
is a grammatical structure (stability property); this property is guaranteed by Algorithm 3.
![]()
Algorithm 2. Construction of![]() .
.
![]()
Algorithm 3. Construction of![]() .
.
Property 2: if ![]() then
then![]() .
.
Property 3: if ![]() is a local update of a replica
is a local update of a replica ![]() such that
such that![]() , then
, then ![]() (consistency property).
(consistency property).
We present below, the proof of the Property 2. The proof of Property 3 can be obtained from the proof of Theorem 3.3 given in [7] .
Proof. Let ![]() be such that
be such that![]() ; let’s show that
; let’s show that![]() .
.
In order to do this, if we consider an internal node n of ![]() labeled
labeled![]() , with its k children,
, with its k children, ![]() labeled
labeled![]() ; it suffices to show that the word
; it suffices to show that the word ![]() belongs to the language denoted by the grammar
belongs to the language denoted by the grammar![]() , admitting the symbol
, admitting the symbol ![]() axiom i.e.
axiom i.e.![]() .
.
Note that one can define a partition ![]() of
of ![]() so that, every tree
so that, every tree ![]() (Figure 3(a)) can be uniquely partitioned into a finite set of maximal subtrees
(Figure 3(a)) can be uniquely partitioned into a finite set of maximal subtrees ![]() (Figure 3(b)) such as, for any subtree
(Figure 3(b)) such as, for any subtree ![]() of the partition, either
of the partition, either![]() , and the labels of the successor nodes of the leaf nodes of
, and the labels of the successor nodes of the leaf nodes of ![]() in t if they exist do not belong to
in t if they exist do not belong to![]() , or
, or ![]() and the labels of the successor nodes of the leaf nodes of
and the labels of the successor nodes of the leaf nodes of ![]() in t if they exist belong to
in t if they exist belong to![]() . When
. When![]() , we say that
, we say that ![]() is of type
is of type ![]() and when
and when![]() , we say that it is of type
, we say that it is of type![]() .
.
Considering the decomposition of t into subtrees of type ![]() and
and ![]() as described above (Figure 3), a node of t can be found either in a subtree of type
as described above (Figure 3), a node of t can be found either in a subtree of type ![]() or in a subtree of type
or in a subtree of type![]() . Moreover, by focusing on a node n of
. Moreover, by focusing on a node n of ![]() and his children
and his children![]() , they can either: 1) all belong to the same subtree of type
, they can either: 1) all belong to the same subtree of type ![]() (Figure 4) or, 2) belong to different subtrees of type
(Figure 4) or, 2) belong to different subtrees of type ![]() in t; in this case, n is a leaf in the subtree in which it appears, and the
in t; in this case, n is a leaf in the subtree in which it appears, and the ![]() are labels of the root nodes (Figure 5) of other subtrees of type
are labels of the root nodes (Figure 5) of other subtrees of type ![]() or, 3) n and some of his children are in the same subtree and the other are each one in their own subtree (Figure 6). Three case studies are therefore to be considered.
or, 3) n and some of his children are in the same subtree and the other are each one in their own subtree (Figure 6). Three case studies are therefore to be considered.
Case 1: ![]() belong to the same subtree
belong to the same subtree ![]() such that
such that![]() . In this case, according to the construction algorithm of
. In this case, according to the construction algorithm of![]() ,
, ![]() and therefore to
and therefore to![]() .
.
![]()
Figure 3. A document (a), its partitioning ((b), (c)) and one of its projections (d).
Case 2: Node n labeled ![]() is a leaf node of a subtree
is a leaf node of a subtree ![]() such that
such that![]() . Let
. Let ![]() be labels of m children of n in t. n has therefore been developed using a
be labels of m children of n in t. n has therefore been developed using a![]() ’s production rule of one of the two forms
’s production rule of one of the two forms![]() , with
, with![]() ; or
; or ![]() with
with![]() . We develop below the second form, the treatment of the first being similar.
. We develop below the second form, the treatment of the first being similar.
![]()
8Reminder: the non-terminals of ![]() are rewritten by the production rules of
are rewritten by the production rules of ![]() by considering the symbols of
by considering the symbols of ![]() as terminals.
as terminals.
There is therefore m sub-terms of t, says![]() , whose roots are respectively labeled by
, whose roots are respectively labeled by ![]() and such that
and such that![]() . According to the
. According to the
![]() ’s building process8, we can partition the word
’s building process8, we can partition the word ![]() in m sub-words:
in m sub-words: ![]() with
with
![]()
As![]() ,
, ![]() according to the construction process of the productions rules of
according to the construction process of the productions rules of ![]() (modulo restructuring symbols).
(modulo restructuring symbols).
Case 3: node n labeled ![]() is an internal node of a subtree
is an internal node of a subtree ![]() such that
such that ![]() and, there is some n’s children with labels not in
and, there is some n’s children with labels not in![]() . As previously, let’s termed
. As previously, let’s termed ![]() labels of the
labels of the ![]() children of n in t. n has therefore been developed using a production rule of the form
children of n in t. n has therefore been developed using a production rule of the form ![]() in which at least one non-terminal belong to
in which at least one non-terminal belong to ![]() and at least one other belong to
and at least one other belong to ![]() (Figure. 6). Let m be the number of non-terminals on the right-hand side of this production belonging to
(Figure. 6). Let m be the number of non-terminals on the right-hand side of this production belonging to ![]() and named as
and named as![]() . As before, there are m sub-terms of t, which we call
. As before, there are m sub-terms of t, which we call![]() , having respectively
, having respectively ![]() as their root labels nodes and such that
as their root labels nodes and such that![]() . Similarly, according to the
. Similarly, according to the![]() ’s building process, we can partition the word
’s building process, we can partition the word ![]() in
in ![]() sub-words:
sub-words:
![]() with
with ![]() and such that
and such that![]() . As
. As![]() ,
, ![]() , we have
, we have
![]()
and then,![]() W
W
3.4. Illustration: Grammatical Structures for the Cooperative Writing of a Small Phone Book
Some of the concepts and algorithms presented in the previous sections are illustrated in this section by considering a simplified case of cooperative writing of a small phone book.
Suppose that two employees of an organization want to cooperate in writing a phone book for their organization. One entry of the book is given by the name (Name), two first names (Fname1 and Fname2), the mails addresses (Emails) and phones numbers (Phones).
A corresponding grammatical structure ![]() describing this phone book is given in the Figure 7. Let us assume that there are two views:
describing this phone book is given in the Figure 7. Let us assume that there are two views: ![]() and
and ![]() for each of the respective employees. By applying the Algorithm 2, we have in Figure 8(a) (resp. Figure 8(b)), the grammatical structure
for each of the respective employees. By applying the Algorithm 2, we have in Figure 8(a) (resp. Figure 8(b)), the grammatical structure ![]() (resp.
(resp.![]() ) resulting from view
) resulting from view ![]() (resp. view
(resp. view![]() ) projection on
) projection on![]() . Note that in
. Note that in![]() , phone’ is a structuring symbol.
, phone’ is a structuring symbol.
4. Conclusion
Asynchronous cooperative editing tools generally allows co-authors to edit complete replicas of a document and perform a posteriori merging [8] [9] [10] [11] [12] regardless if document is structured or not; It’s the case in many tools
![]()
Figure 7. A grammatical Structure ![]() of a phone book.
of a phone book.
![]()
Figure 8. Two local models resulting from the projection on global model of Figure 7 according to view ![]() (a) and view
(a) and view ![]() (b).
(b).
of version managing like CVs for unstructured documents (textual merge) [13] .
In the case of structured editing, all co-authors have the same document model and the merging of complete replicas relies on this model (syntactic merging software) [14] [15] . We were interested in this paper to an innovative case―we did not find any study that was done in this direction―in which the co-authors act on partial replicas of the overall document and each with a local model allowing him to validate locally updates made on its (partial) local replica.
We proposed as a document model in this context, grammatical structures allowing both to specify the model for the global document, and local models - for partial replicas―dedicated to each co-author. Furthermore, we have defined a projection operation to automatically derive the local models (grammatical structures) of documents from the global one.
Stability and consistency are some of the major properties enjoyed by grammatical structures. Consistency ensures that, every document validated locally with the local grammatical structure is always the projection of at least one valid document according to the overall grammatical structure: the gra- mmatical structures thus offer to the different co-authors a suitable means of carrying out local syntactic validations of the asynchronously edited documents, while ensuring consistency.
One can further this study by focusing on bottom-up construction of grammatical structures. The goal is to propose a “grammatical structures merger” similar to the “documents merger” presented in [4] .
NOTES
![]()
1For a given co-author, some parts of the document may contain sensitive information. It is preferable that he is not even informed of the presence of this information in the document. As we shall see later, the projection operation will resolve this confidentiality problem.
2Handled documents pass through the network. They will circulate all the more quickly as their size is reduced. For this reason, the replica of the document to be sent to a co-author must contain only the parts which are of obvious interest to him: it’s a partial replica. Here too, the projection operation will solve this concern.
![]()
3The problem of re-synchronization―consistent expansion―a posteriori is presented and resolved in [4] where we can also find many basic definitions reused here.
![]()
4The DTD (Document Type Definition) for example are special cases of extended context free grammars verifying property of one-unambiguity [5] .
![]()
5As in [6] , we are just interested by non recursive models. This is not an aberration because, from statistical point of view, non recursive DTDs are more frequent than recursive ones.