Common Fixed Point Theorems in Metric Space by Altering Distance Function

Vishnu Narayan Mishra^1,2*, Balaji Raghunath Wadkar³, Ramakant Bhardwaj⁴, Idrees A. Khan⁵, Basant Singh³

¹Applied Mathematics & Humanities Department, S.V. National Institute of Technology, Gujarat, India.
²Department of Mathematics, Indira Gandhi National Tribal University, Madhya Pradesh, India.
³Department of Mathematics, AISECT University, Bhopal, India.
⁴Department of Mathematics, TIT Group of Institutes, Anand Nagar, India.
⁵Department of Mathematics, Integral University, Lucknow, India.

DOI: 10.4236/apm.2017.76020                

Abstract

In the present paper, we prove two theorems. In first theorem, we prove fixed point result for self-maps in the metric space under contractive condition of integral type by altering distance. In second result, we prove a unique common fixed point theorem by considering four sub compatible maps under a contractive condition of integral type.

Keywords

Altering Distance Function, Sub Compatible

1. Introduction and preliminaries

In [1] , Khan introduced and proved fixed point results by the altering distance in metric space. Aliouche [2] proved common fixed point results in symmetric space for weakly compatible mappings under contractive condition of integral type. In [3] , Babu generalized and proved fixed point results using control function. Later Bouhadjera and Godet [4] generalized concept of pair sub compatible maps and proved fixed point results. Also Chaudhari [5] [6] , Chugh & Kumar [7] , Naidu [8] , Sastry et al. [9] generalized and proved some fixed point results. Recently in [10] [11] , Hosseni used contractive rule of integral type by altering distance and generalized common fixed point results. Many authors proved fixed point results with different techniques in different spaces (see [12] - [17] ). In [18] [19] [20] [21] , Wadkar et al. proved fixed point theorems using the concept of soft metric space. In the present paper, we prove two theorems on fixed point under contraction rule of integral type in metric space by altering distance function, first for self map and second for a pair of sub compatible maps. Our results are motivated by V. R. Hosseni, Neda Hosseni.

Definition 1.1: A function $\psi :R^{+}\to R^{+}=\left[0,1\right)$ is an altering distance functions if $\psi$ is continuous with monotone increasing in all variables and $\psi \left(x_1,x_2,x_3,\cdots ,x_n\right)=0$ if $x_1=x_2=x_3=\cdots =x_n=0.$

The collection of all altering distance is denoted by ${\Psi }_n$ .

Now let us define a function $m\left(y\right)$ by $m\left(y\right)=\psi \left(y,y,y,y,\cdots ,y\right)$ for $y\in \left[0,\infty \right)$ , clearly $m\left(y\right)=0$ if and only if $y=0$ .

Examples of $\psi$ are $\psi \left(f_1,f_2,f_3,\cdots ,f_n\right)=\mu \max \left\{f_1,f_2,f_3,\cdots ,f_n\right\},$ for $\mu >0$ , (1)

$\psi \left(f_1,f_2,f_3,\cdots ,f_n\right)=f_n^{a_1}+f_n^{a_2}+f_n^{a_3}+\cdots +f_n^{a_n},a_1,a_2,\cdots ,a_n\ge 1.$ (2)

Definition 1.2: The maps $p,q:E\to E$ of metric space $\left(E,\sigma \right)$ are called as sub compatible if and only if the sequence $\left\{e_n\right\}$ in E such that $\underset{n\to \infty }{\lim }{p}_n=\underset{n\to \infty }{\lim }{q}_n=t,t\in E$ and which satisfies $\underset{n\to \infty }{\lim }\sigma \left(pq{e}_n,qp{e}_n\right)=0.$

Example 1.3: Let $E=\left[0,\infty \right)$ we define p & q with metric $\sigma$ as follows

$p\left(e\right)=e^2$ & $q\left(e\right)=\{\begin{array}{l}e+6\text{if}e\in \left[4,9\right]\cup \left(27,\infty \right)\hfill \\ e^2,\text{if}e\in \left[9,27\right]\hfill \end{array}$ (3)

Let us define the sequence $\left\{e_n\right\}$ in E as $e_n=3+\frac{1}{n}$ , for $n=0,1,2,\cdots$ then

$\underset{n\to \infty }{\lim }p{e}_n=\underset{n\to \infty }{\lim }{e}_n^2=9=\underset{n\to \infty }{\lim }q{e}_n=\underset{n\to \infty }{\lim }\left(e_n+6\right),$ (4)

and $\underset{n\to \infty }{\lim }pq\left(e_n\right)=\underset{n\to \infty }{\lim }p\left(e_n+6\right)=\underset{n\to \infty }{\lim }{\left(e_n+6\right)}^2=81\text{when}n\to \infty ,$ (5)

$\underset{n\to \infty }{\lim }qp{e}_n=\underset{n\to \infty }{\lim }q{e}_n^2={\left(e_n^2\right)}^2=\underset{n\to \infty }{\lim }{\left(e_n\right)}^4=81\text{when}n\to \infty .$ (6)

Thus, we have $\underset{n\to \infty }{\lim }\sigma \left(pq{e}_n,qp{e}_n\right)=0$ . (7)

Hence maps p and q are sub-compatible.

On the other hand, we have $pe=qe$ if and only if $e=3$ , $pq\left(3\right)=p\left(9\right)=81$ and $qp\left(3\right)=q\left(9\right)=9+6=15.$

Then $p\left(3\right)=9=q\left(3\right)$ but $pq\left(3\right)=81\ne 15=qp\left(3\right)$ , hence p and q are not OWC (Oscillatory weakly commuting).

2. Main Result

Theorem 2.1: Let us consider the mappings $U,V:E\to E$ of complete metric space $\left(E,\sigma \right)$ be such that for all $c,d\in E$

$\begin{array}{c}{\displaystyle {\int }_0^{{\varphi }_1\left(\sigma \left(Uc,Vd\right)\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\psi }_1\left(\sigma \left(c,d\right),\sigma \left(Uc,,c\right),\sigma \left(Vd,d\right),\frac{1}{2}\left\{\sigma \left(Vd,c\right)+\sigma \left(Uc,d\right)\right\},\frac{1}{2}\left\{\sigma \left(c,d\right)+\sigma \left(Uc,c\right)\right\}\right)}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{{\psi }_2\left(\sigma \left(c,d\right),\sigma \left(Uc,,c\right),\sigma \left(Vd,d\right),\frac{1}{2}\left\{\sigma \left(Vd,c\right)+\sigma \left(Uc,d\right)\right\},\frac{1}{2}\left\{\sigma \left(c,d\right)+\sigma \left(Uc,c\right)\right\}\right)}\eta \left(y\right)\text{d}y},\end{array}$ (8)

where ${\psi }_1,{\psi }_2\in {\Psi }_5$ with ${\varphi }_1=\psi \left(e,e,e,e,e\right)$ , $e\in \left[0,\infty \right)$ and Lebesgue-integr- able mapping $\eta :R^{+}\to R^{+}$ , which is positive, sum able, and for each $\in >0,{\displaystyle {\int }_0^{\in }\eta \left(y\right)\text{d}y>0}$ , then there exist a unique common fixed point in E for U and V.

Proof: Consider arbitrary point $e_0$ of E, for $n=1,2,3,\cdots$ we have

$e_{2n+1}=U{e}_{2n}$

and $e_{2n+2}=V{e}_{2n+1}$ .

Let $r_n=\sigma \left(e_n,e_{n+1}\right)$ (9)

Substituting $c=e_{2n}$ and $d=e_{2n+1}$ in Equation (8), then for all $n=1,2,3,\cdots$ we have

$\begin{array}{l}{\displaystyle {\int }_0^{{\varphi }_1\left(\sigma \left(U{e}_{2n},V{e}_{2n+1}\right)\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\varphi }_1\left(\sigma \left(e_{2n+1},e_{2n+2}\right)\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\psi }_1\left(\sigma \left(e_{2n},e_{2n+1}\right),\sigma \left(U{e}_{2n},e_{2n}\right),\sigma \left(V{e}_{2n+1},e_{2n+1}\right),\frac{1}{2}\left\{\begin{array}{l}\sigma \left(V{e}_{2n+1},e_{2n}\right)\\ +\sigma \left(U{e}_{2n},e_{2n+1}\right)\end{array}\right\},\frac{1}{2}\left\{\begin{array}{l}\sigma \left(e_{2n},e_{2n+1}\right)+\\ \sigma \left(U{e}_{2n},e_{2n}\right)\end{array}\right\}\right)}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{{\psi }_2\left(\sigma \left(e_{2n},e_{2n+1}\right),\sigma \left(U{e}_{2n},e_{2n}\right),\sigma \left(V{e}_{2n+1},e_{2n+1}\right),\frac{1}{2}\left\{\begin{array}{l}\sigma \left(V{e}_{2n+1},e_{2n}\right)\\ +\sigma \left(U{e}_{2n},e_{2n+1}\right)\end{array}\right\},\frac{1}{2}\left\{\begin{array}{l}\sigma \left(e_{2n},e_{2n+1}\right)\\ +\sigma \left(U{e}_{2n},e_{2n}\right)\end{array}\right\}\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\psi }_1\left(\sigma \left(e_{2n},e_{2n+1}\right),\sigma \left(e_{2n+1},e_{2n}\right),\sigma \left(e_{2n+2},e_{2n+1}\right),\frac{1}{2}\left\{\begin{array}{l}\sigma \left(e_{2n+2},e_{2n}\right)\\ +\sigma \left(e_{2n+1},e_{2n+1}\right)\end{array}\right\},\frac{1}{2}\left\{\begin{array}{l}\sigma \left(e_{2n},e_{2n+1}\right)\\ +\sigma \left(e_{2n+1},e_{2n}\right)\end{array}\right\}\right)}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{{\psi }_2\left(\sigma \left(e_{2n},e_{2n+1}\right),\sigma \left(e_{2n+1},e_{2n}\right),\sigma \left(e_{2n+2},e_{2n+1}\right),\frac{1}{2}\left\{\begin{array}{l}\sigma \left(e_{2n+2},e_{2n}\right)\\ +\sigma \left(e_{2n+1},e_{2n+1}\right)\end{array}\right\},\frac{1}{2}\left\{\begin{array}{l}\sigma \left(e_{2n},e_{2n+1}\right)\\ +\sigma \left(e_{2n+1},e_{2n}\right)\end{array}\right\}\right)}\eta \left(y\right)\text{d}y}\end{array}$

Using Equation (9) for all $n=1,2,3,\cdots$ we get

$\begin{array}{c}{\displaystyle {\int }_0^{{\varphi }_1\left(r_{2n+1}\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\psi }_1\left(r_{2n},r_{2n},r_{2n+1}\frac{1}{2}\left\{r_{2n+1}+r_{2n}+0\right\},\frac{1}{2}\left\{r_{2n}+r_{2n}\right\}\right)}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{{\psi }_2\left(r_{2n},r_{2n},r_{2n+1}\frac{1}{2}\left\{r_{2n+1}+r_{2n}+0\right\},\frac{1}{2}\left\{r_{2n}+r_{2n}\right\}\right)}\eta \left(y\right)\text{d}y}\end{array}$ (10)

As $r_{2n+1}>r_{2n}$ implies that $r_{2n+1}+r_{2n}\le 2r_{2n+1}$ , so we have

${\displaystyle {\int }_0^{{\varphi }_1\left(r_{2n+1}\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\psi }_1\left(r_{2n},r_{2n},r_{2n+1}{r}_{2n+1},r_{2n}\right)}\eta \left(y\right)\text{d}y}={\displaystyle {\int }_0^{{\varphi }_1\left(r_{2n+1}\right)}\eta \left(y\right)\text{d}y}$ (11)

Now by monotone increase of ${\psi }_1$ in all variables and using the property that ${\psi }_2\left(r_{2n},r_{2n},r_{2n+1},r_{2n+1},r_{2n}\right)\ne 0$ whenever $r_{2n+1}\ne 0$ , we get a contradiction i.e. $r_{2n+1}$ not greater than $r_{2n}$ . Hence we have $r_{2n+1}\le r_{2n}$ , for

$n=0,1,2,3,\cdots$ (12)

Substituting $c=e_{2n-1},d=e_{2n}$ in Equation (8) we have

${\displaystyle {\int }_0^{{\varphi }_1\left(r_{2n}\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\psi }_1\left(r_{2n-1},r_{2n-1},r_{2n},r_{2n},r_{2n-1}\right)}\eta \left(y\right)\text{d}y}-{\displaystyle {\int }_0^{{\psi }_2\left(r_{2n-1},r_{2n-1},r_{2n},r_{2n},r_{2n-1}\right)}\eta \left(y\right)\text{d}y}$ (13)

By using (12) we consider

$r_{2n+2}\le r_{2n+1}$ (14)

From (10) and (12) we obtain

$r_{n+1}\le r_n$ (15)

From (8) & (11) for all $n=1,2,3,\cdots$ , we have

${\displaystyle {\int }_0^{{\varphi }_1\left(r_{n+1}\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\psi }_1\left(r_n\right)}\eta \left(y\right)\text{d}y}-{\displaystyle {\int }_0^{{\psi }_2\left(r_n\right)}\eta \left(y\right)\text{d}y}$

then

${\displaystyle {\int }_0^{{\varphi }_2\left(r_{n+1}\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\varphi }_1\left(r_n\right)}\eta \left(y\right)\text{d}y}-{\displaystyle {\int }_0^{{\varphi }_1\left(r_{n+1}\right)}\eta \left(y\right)\text{d}y}$

Taking summation in above equation we obtain

${\displaystyle \underset{0}{\overset{\infty }{\sum }}{\displaystyle {\int }_0^{{\varphi }_2\left(r_{n+1}\right)}\eta \left(y\right)\text{d}y}}\le {\displaystyle {\int }_0^{{\varphi }_1\left(r_0\right)}\eta \left(y\right)\text{d}y}<\infty$ ,

which implies ${\varphi }_2\left(r\right)\to 0$ as $n\to \infty$ . (16)

Now from (13) sequence $\left\{r_n\right\}$ is convergent and as $n\to \infty$ , $r_n\to r.$ We know that $\varphi$ is continuous and from Equation (14) we obtain ${\varphi }_2\left(r\right)=0$ which implies that $r=0$ , i.e. as

$n\to \infty ,$ $r=\sigma \left(e_{n+1},e_n\right)\to 0.$ (17)

We now show that the sequence $\left\{e_n\right\}$ is a Cauchy sequence in E. Keeping in mind Equation (15) it is require to show that ${\left\{e_{2s}\right\}}_{s=1}^{\infty }\subset \left\{e_n\right\}$ is a Cauchy sequence. If ${\left\{e_{2s}\right\}}_{s=1}^{\infty }$ is not a Cauchy sequence of natural number $\left\{2m\left(k\right)\right\},\left\{2n\left(k\right)\right\}$ such that $n\left(k\right)>m\left(k\right)$ , $\sigma \left(e_{2m\left(k\right)},e_{2n\left(k\right)}\right)\ge \in$

$\sigma \left(e_{2m\left(k\right)},e_{2n\left(k\right)-1}\right)<\in$ (18)

Hence using (16)

$\begin{array}{l}\in <\sigma \left(e_{2m\left(k\right)},e_{2n\left(k\right)}\right)\\ \le \sigma \left(e_{2m\left(k\right)},e_{2n\left(k\right)-1}\right)+\sigma \left(e_{2n\left(k\right)},e_{2n\left(k\right)-1}\right)\\ <\in +\sigma \left(e_{2n\left(k\right)},e_{2n\left(k\right)-1}\right).\end{array}$

Taking $k\to \infty$ in the inequality above & by result of Equation (15), we arrive at

$\underset{n\to \infty }{\lim }\sigma \left(e_{2m\left(k\right)},e_{2n\left(k\right)}\right)=\in$ . (19)

For all $k=1,2,3,\cdots$

$\sigma \left(e_{2n\left(k\right)+1},e_{2m\left(k\right)}\right)\le \sigma \left(e_{2n\left(k\right)+1},e_{2n\left(k\right)}\right)+\sigma \left(e_{2n\left(k\right)},e_{2m\left(k\right)}\right)$ (20)

Also for $k=1,2,3,\cdots$

$\sigma \left(e_{2n\left(k\right)},e_{2m\left(k\right)}\right)\le \sigma \left(e_{2n\left(k\right)},e_{2n\left(k\right)+1}\right)+\sigma \left(e_{2n\left(k\right)+1},e_{2m(k)}\right)$ . (21)

Making $k\to \infty$ in (18) & (19) respectively by using (15) & (17) we have

$\underset{k\to \infty }{\lim }\sigma \left(e_{2n\left(k\right)+1},e_{2m\left(k\right)}\right)\le \in$

and $\in \le \underset{k\to \infty }{\lim }\sigma \left(e_{2n\left(k\right)+1},e_{2m\left(k\right)}\right)$

Therefore, $\underset{k\to \infty }{\lim }\sigma \left(e_{2n\left(k\right)+1},e_{2m\left(k\right)}\right)=\in$ , for $k=1,2,3,\cdots$ (22)

$\sigma \left(e_{2n\left(k\right)},e_{2m\left(k\right)-1}\right)\le \sigma \left(e_{2n\left(k\right)},e_{2m\left(k\right)}\right)+\sigma \left(e_{2m\left(k\right)},e_{2m\left(k\right)-1}\right),$

$\sigma \left(e_{2n\left(k\right)},e_{2m\left(k\right)}\right)\le \sigma \left(e_{2n\left(k\right)},e_{2m\left(k\right)-1}\right)+\sigma \left(e_{2m\left(k\right)-1},e_{2m\left(k\right)}\right).$

Taking $k\to \infty$ in the above two inequalities and using (15) & (17) we obtain

$\underset{n\to \infty }{\lim }\sigma \left(e_{2n\left(k\right)},e_{2m\left(k\right)-1}\right)=\in$ . (23)

Putting $c=e_{2n\left(k\right)},d=e_{2m\left(k\right)-1}$ in (8), for all $k=1,2,3,\cdots$ , we obtain

$\begin{array}{l}{\displaystyle {\int }_0^{{\varphi }_1\sigma \left(e_{2n\left(k\right)+1},e_{2m\left(k\right)}\right)}\eta \left(y\right)\text{d}y}={\displaystyle {\int }_0^{{\varphi }_1\sigma \left(U{e}_{2n\left(k\right)},V{e}_{2m\left(k\right)-1}\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\psi }_1\left(\sigma \left(e_{2n},e_{2m\left(k\right)-1}\right),\sigma \left(e_{2n\left(k\right)+1},e_{2n}\right),\sigma \left(e_{2m\left(k\right)},e_{2m\left(k\right)-1}\right),\frac{1}{2}\left\{\begin{array}{l}\sigma \left(e_{2m\left(k\right)},e_{2n\left(k\right)}\right)\\ +\sigma \left(e_{2n\left(k\right)+1},e_{2m\left(k\right)-1}\right)\end{array}\right\},\frac{1}{2}\left\{\begin{array}{l}\sigma \left(e_{2n\left(k\right)},e_{2m\left(k\right)-1}\right)\\ +\sigma \left(e_{2n\left(k\right)+1},e_{2n}\left(k\right)\right)\end{array}\right\}\right)}\mathrm{\eta (y)dy}}\\ -{\displaystyle {\int }_0^{{\psi }_2\left(\sigma \left(e_{2n},e_{2m\left(k\right)-1}\right),\sigma \left(e_{2n\left(k\right)+1},e_{2n}\right),\sigma \left(e_{2m\left(k\right)},e_{2m\left(k\right)-1}\right),\frac{1}{2}\left\{\begin{array}{l}\sigma \left(e_{2m\left(k\right)},e_{2n\left(k\right)}\right)\\ +\sigma \left(e_{2n\left(k\right)+1},e_{2m\left(k\right)-1}\right)\end{array}\right\},\frac{1}{2}\left\{\begin{array}{l}\sigma \left(e_{2n\left(k\right)},e_{2m\left(k\right)-1}\right)\\ +\sigma \left(e_{2n\left(k\right)+1},e_{2n}\left(k\right)\right)\end{array}\right\}\right)}\mathrm{\eta (y)dy}}\end{array}$

Now in above inequality if we take $k\to \infty$ and by using results of (15), (20) & (21) we get

${\displaystyle {\int }_0^{{\varphi }_1(\in )}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\psi }_1\left(\in ,0,0,\in ,\frac{1}{2}\in \right)}\eta \left(y\right)\text{d}y}-{\displaystyle {\int }_0^{{\psi }_2\left(\in ,0,0,\in ,\frac{1}{2}\in \right)}\eta \left(y\right)\text{d}y}.$

Then ${\varphi }_1(\in )\le {\psi }_1\left(\in ,0,0,\in ,\frac{1}{2}\in \right)-{\psi }_2\left(\in ,0,0,\in ,\frac{1}{2}\in \right)={\varphi }_1(\in ).$

This is due to monotone increasing fact of ${\psi }_1$ in its variable and by using property of ${\psi }_2$ that ${\psi }_2\left(y_1,y_2,y_3,y_4,y_5\right)=0,$ if and only if $y_1=y_2=y_3=y_4=y_5=0$ .

From the above inequality we get a contradiction. So that $\in =0$ . This establishes convergent sequence in $\left(E,\sigma \right)$ .

Let $e_n\to z$ as $n\to \infty$ . (24)

Substituting $c=e_{2n},$ $d=z$ in (8) for all $n=1,2,3,\cdots$

$\begin{array}{l}{\displaystyle {\int }_0^{{\varphi }_1\left(\sigma \left(e_{2n+1},Vz\right)\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\psi }_1\left(\sigma \left(e_{2n},z\right),\sigma \left(e_{2n+1},e_{2n}\right),\sigma \left(Vz,z\right),\frac{1}{2}\left\{\sigma \left(Vz,e_{2n}\right)+\sigma \left(e_{2n+1},z\right)\right\},\frac{1}{2}\left\{\sigma \left(e_{2n},z\right)+\sigma \left(e_{2n+1},e_{2n}\right)\right\}\right)}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{{\psi }_2\left(\sigma \left(e_{2n},z\right),\sigma \left(e_{2n+1},e_{2n}\right),\sigma \left(Vz,z\right),\frac{1}{2}\left\{\sigma \left(Vz,e_{2n}\right)+\sigma \left(e_{2n+1},z\right)\right\},\frac{1}{2}\left\{\sigma \left(e_{2n},z\right)+\sigma \left(e_{2n+1},e_{2n}\right)\right\}\right)}\eta \left(y\right)\text{d}y}\end{array}$

Taking limit n tends to infinity in the above inequality and using continuity of ${\psi }_1$ and ${\psi }_2$ and Equations (15), (22) we get

$\begin{array}{l}{\displaystyle {\int }_0^{{\varphi }_1\left(\sigma (z,Vz)\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\psi }_1\left(\sigma \left(z,z\right),\sigma \left(z,z\right),\sigma \left(Vz,z\right),\frac{1}{2}\left\{\sigma \left(Vz,z\right)\right\},0\right)}\eta \left(y\right)\text{d}y}-{\displaystyle {\int }_0^{{\psi }_2\left(\sigma \left(z,z\right),\sigma \left(z,z\right),\sigma \left(Vz,z\right),\frac{1}{2}\left\{\sigma \left(Vz,z\right)\right\},0\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\psi }_1\left(0,0,\sigma \left(Vz,z\right),\frac{1}{2}\left\{\sigma \left(Vz,z\right)\right\},0\right)}\eta \left(y\right)\text{d}y}-{\displaystyle {\int }_0^{{\psi }_2\left(0,0,\sigma \left(Vz,z\right),\frac{1}{2}\left\{\sigma \left(Vz,z\right)\right\},0\right)}\eta \left(y\right)\text{d}y}\end{array}$

If $\left(Vz,z\right)\ne 0$ then monotone increasing ${\psi }_1$ and ${\psi }_2$ are monotone increasing and ${\psi }_2\left(y_1,y_2,y_3,y_4,y_5\right)=0,$ if and only if $y_1=y_2=y_3=y_4=y_5=0$ , we obtain

${\displaystyle {\int }_0^{{\varphi }_1\left(\sigma (z,Vz\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\varphi }_1\left(\sigma (z,Vz\right)}\eta \left(y\right)\text{d}y}.$

This contradiction, hence we obtain $\left(Vz,z\right)=0.$ (25)

In similar way we prove that $z=Uz.$ Hence $z=Uz=Vz.$ (26)

Hence (25) & (26) shows that z is a common fixed point of U and V.

Theorem 2.2: Let $\left(E,\sigma \right)$ be a complete metric space and p, q, U and V be four mappings from E to itself such that

$\begin{array}{l}{\displaystyle {\int }_0^{{\varphi }_1\left(\sigma \left(ps,qt\right)\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\psi }_1\left(\sigma \left(Us,Vt\right),\sigma \left(Us,qt\right),\sigma \left(ps,Vt\right),\sigma \left(Us,ps\right),\sigma \left(Vt,qt\right),\frac{1}{2}\left\{\sigma \left(qt,Us\right)+\sigma \left(ps,Vt\right)\right\},\frac{1}{2}\left\{\sigma \left(Us,Vt\right)+\sigma \left(ps,Us\right)\right\}\right)}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{{\psi }_2\left(\sigma \left(Us,Vt\right),\sigma \left(Us,qt\right),\sigma \left(ps,Vt\right),\sigma \left(Us,ps\right),\sigma \left(Vt,qt\right),\frac{1}{2}\left\{\sigma \left(qt,Us\right)+\sigma \left(ps,Vt\right)\right\},\frac{1}{2}\left\{\sigma \left(Us,Vt\right)+\sigma \left(ps,Us\right)\right\}\right)}\eta \left(y\right)\text{d}y},\end{array}$ (27)

for all $s,t\in E$ , where ${\psi }_1,{\psi }_2\in {\Psi }_7$ , ${\varphi }_1=\psi \left(e,e,e,e,e,e,e\right)$ , for $e\in \left[0,\infty \right)$ .

i: One of the four mappings p, q, U and V is continuous.

ii: (p, U) & (q, V) are sub compatible.

iii: The pairs $p\left(s\right)\subseteq V\left(s\right)$ and $q\left(s\right)\subseteq U\left(s\right)$ .

iv: Where $\eta :R^{+}\to R^{+}$ is Lebesgue-integrable mappings, which is sum able, non negative and such that for each $\in >0,{\displaystyle {\int }_0^{\in }\eta (y)dy>0}$ .

Then p, q, U and V have a unique common fixed point in E.

Proof: Consider arbitrary point $e_0\in E$ , we construct the sequence $\left\{e_n\right\}$ and $\left\{w_n\right\}$ in E such that

$p{e}_{2n}=V{e}_{2n+1}=w_{2n}$ and $q{e}_{2n+1}=U{e}_{2n+2}=w_{n+1}$ , $n=0,1,2,\cdots$

Let $r_n=\sigma \left(w_n,w_{n+1}\right)$ , Substitution $s=e_{2n}$ and $t=e_{2n+1}$ in (27) we have

$\begin{array}{l}{\displaystyle {\int }_0^{{\varphi }_1\left(\sigma \left(p{e}_{2n},q{e}_{2n+1}\right)\right)}\eta \left(y\right)\text{d}y}={\displaystyle {\int }_0^{{\varphi }_1\left(\sigma \left(e_{2n+1},e_{2n+2}\right)\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{\begin{array}{l}{\psi }_1(\sigma \left(U{e}_{2n},V{e}_{2n+1}\right),\sigma \left(U{e}_{2n},q{e}_{2n+1}\right),\sigma \left(p{e}_{2n+1},V{e}_{2n+1}\right),\sigma \left(U{e}_{2n},p{e}_{2n}\right),\sigma \left(V{e}_{2n+1},q{e}_{2n+1}\right),\\ \frac{1}{2}\left\{\sigma \left(q{e}_{2n+1},U{e}_{2n}\right)+\sigma \left(p{e}_{2n},V{e}_{2n+1}\right)\right\},\frac{1}{2}\left\{\sigma \left(U{e}_{2n},V{e}_{2n+1}\right)+\sigma \left(p{e}_{2n},U{e}_{2n}\right)\right\})\end{array}}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{\begin{array}{l}{\psi }_2(\sigma \left(U{e}_{2n},V{e}_{2n+1}\right),\sigma \left(U{e}_{2n},q{e}_{2n+1}\right),\sigma \left(p{e}_{2n+1},V{e}_{2n+1}\right),\sigma \left(U{e}_{2n},p{e}_{2n}\right),\sigma \left(V{e}_{2n+1},q{e}_{2n+1}\right),\\ \frac{1}{2}\left\{\sigma \left(q{e}_{2n+1},U{e}_{2n}\right)+\sigma \left(p{e}_{2n},V{e}_{2n+1}\right)\right\},\frac{1}{2}\left\{\sigma \left(U{e}_{2n},V{e}_{2n+1}\right)+\sigma \left(p{e}_{2n},U{e}_{2n}\right)\right\})\end{array}}\eta \left(y\right)\text{d}y}\end{array}$

$\begin{array}{l}{\displaystyle {\int }_0^{\varphi \left(\sigma \left(w_{2n},w_{2n+1}\right)\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{\begin{array}{l}{\psi }_1(\sigma \left(w_{2n-1},w_{2n}\right),\sigma \left(w_{2n-1},w_{2n+1}\right),\sigma \left(w_{2n+1},w_{2n}\right),\sigma \left(w_{2n-1},w_{2n}\right),\sigma \left(w_{2n},w_{2n+1}\right),\\ \frac{1}{2}\left\{\sigma \left(w_{2n+1},w_{2n}\right)+\sigma \left(w_{2n},w_{2n}\right)\right\},\frac{1}{2}\sigma \left(w_{2n-1},w_{2n}\right)+\sigma \left(w_{2n},w_{2n-1}\right))\end{array}}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{\begin{array}{l}{\psi }_2(\sigma \left(w_{2n-1},w_{2n}\right),\sigma \left(w_{2n-1},w_{2n+1}\right),\sigma \left(w_{2n+1},w_{2n}\right),\sigma \left(w_{2n-1},w_{2n}\right),\sigma \left(w_{2n},w_{2n+1}\right),\\ \frac{1}{2}\left\{\sigma \left(w_{2n+1},w_{2n}\right)+\sigma \left(w_{2n},w_{2n}\right)\right\},\frac{1}{2}\sigma \left(w_{2n-1},w_{2n}\right)+\sigma \left(w_{2n},w_{2n-1}\right))\end{array}}\eta \left(y\right)\text{d}y}\end{array}$

$\begin{array}{c}{\displaystyle {\int }_0^{{\varphi }_1\left(r_{2n}\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\psi }_1\left(r_{2n-1},r_{2n-1}+r_{2n},r_{2n,}{r}_{2n-1},r_{2n},\frac{1}{2}\left\{r_{2n}\right\},\frac{1}{2}\left\{r_{2n-1}+r_{2n-1}\right\}\right)}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{{\psi }_2\left(r_{2n-1},r_{2n-1}+r_{2n},r_{2n,}{r}_{2n-1},r_{2n},\frac{1}{2}\left\{r_{2n}\right\},\frac{1}{2}\left\{r_{2n-1}+r_{2n-1}\right\}\right)}\eta \left(y\right)\text{d}y}\end{array}$

If $r_{2n+1}\le r_{2n}$ then $r_{2n+1}+r_{2n}\le 2r_{2n}$ and

$\begin{array}{c}{\displaystyle {\int }_0^{{\varphi }_1\left(r_{2n}\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\psi }_1\left(r_{2n-1},2r_{2n},r_{2n,}{r}_{2n-1},r_{2n},\frac{1}{2}\left\{r_{2n}\right\},r_{2n-1}\right)}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{{\psi }_2\left(r_{2n-1},2r_{2n},r_{2n,}{r}_{2n-1},r_{2n},\frac{1}{2}\left\{r_{2n}\right\},r_{2n-1}\right)}\eta \left(y\right)\text{d}y}\\ <{\displaystyle {\int }_0^{{\varphi }_1\left(r_{2n}\right)}\eta \left(y\right)\text{d}y}.\end{array}$ (28)

Thus we arrive at a contradiction. Hence $r_{2n}\le r_{2n-1}$ , similarly by substituting $s=r_{2n+2},t=r_{2n+1}$ in (27) we can prove that, $r_{2n+1}\le r_{2n}$ , for $n=0,1,2,\cdots$ . Thus $r_{n+1}\le r_n$ , for $n=0,1,2,\cdots$ . Hence the sequence $\left\{r_n\right\}$ is sequence of positive real numbers, which is decreasing and converges to $r\in R$ .

Let $m=\underset{n\to \infty }{\lim }\frac{1}{2}d\left(w_n,w_{n+2}\right)$ . Taking $n\to \infty$ in (27) we have

$\begin{array}{c}{\displaystyle {\int }_0^{{\varphi }_1\left(r_{2n}\right)}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\psi }_1\left(r,r,r,r,r,r,r\right)}\eta \left(y\right)\text{d}y}-{\displaystyle {\int }_0^{{\psi }_2\left(r,r,r,r,r,r,m\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\varphi }_1\left(r\right)}\eta \left(y\right)\text{d}y}-{\displaystyle {\int }_0^{{\psi }_2\left(r,r,r,r,r,r,m\right)}\eta \left(y\right)\text{d}y}.\end{array}$

$\begin{array}{l}\text{Thus}{\psi }_2\left(r,r,r,r,r,r,m\right)=0\text{So}\text{that}r=m=0.\\ \text{Hence}\underset{n\to \infty }{\lim }d\left(y_n,y_{n+1}\right)=0\end{array}$ (29)

In view of (29), to prove sequence $\left\{w_n\right\}$ is a Cauchy sequence it is sufficient to prove the subsequence $\left\{w_{2n}\right\}$ of sequence $\left\{w_n\right\}$ is a Cauchy sequence. If $\left\{w_{2n}\right\}$ is not a Cauchy sequence there exist $\in >0$ & sequence of natural numbers $\left\{2m\left(k\right)\right\}$ & $\left\{2n\left(k\right)\right\}$ which are monotone increasing such that $n\left(k\right)>m\left(k\right)$ .

$\sigma \left(w_{2m\left(k\right)},w_{2n\left(k\right)}\right)\ge \in \&\sigma \left(w_{2m\left(k\right)},w_{2n\left(k\right)-2}\right)<\in .$ (30)

Then from (29) we have

$\begin{array}{l}\in <\sigma \left(w_{2m\left(k\right)},w_{2n\left(k\right)}\right)\\ \le \sigma \left(w_{2m\left(k\right)},w_{2n\left(k\right)-2}\right)+\sigma \left(w_{2n\left(k\right)-1},w_{2n\left(k\right)-2}\right)+\sigma \left(w_{2n\left(k\right)-1},w_{2n\left(k\right)}\right)\\ <\in +\sigma \left(w_{2n\left(k\right)-1},w_{2n\left(k\right)-2}\right)+\sigma \left(w_{2n\left(k\right)-1},w_{2n\left(k\right)}\right).\end{array}$ (31)

Taking $k\to \infty$ and using (29) we have

$\underset{n\to \infty }{\lim }\sigma \left(w_{2m\left(k\right)},w_{2n\left(k\right)}\right)=\in .$ (32)

Taking $k\to \infty$ using (29) & (30) in

$\left|\sigma \left(w_{2m\left(k\right)},w_{2n\left(k\right)+1}\right)-\sigma \left(w_{2m\left(k\right)},w_{2n\left(k\right)}\right)\right|\le \sigma \left(w_{2n\left(k\right)},w_{2n\left(k\right)+1}\right).$ (33)

We get $\underset{n\to \infty }{\lim }\sigma \left(w_{2n\left(k\right)+1},w_{2m\left(k\right)}\right)=\in .$ (34)

Letting $k\to \infty$ and from Equations (29) & (30) in

$\left|\sigma \left(w_{2m\left(k\right)-1},w_{2n\left(k\right)}\right)-\sigma \left(w_{2m\left(k\right)},w_{2n\left(k\right)}\right)\right|\le \sigma \left(w_{2m\left(k\right)},w_{2m\left(k\right)-1}\right).$

We get $\underset{k\to \infty }{\lim }\sigma \left(w_{2m\left(k\right)},w_{2m\left(k\right)-1}\right)=\in .$ (35)

Putting $s=x_{2m\left(k\right)},t=x_{2n\left(k\right)-1}$ in (27), for all $k=1,2,3,\cdots$ we obtain

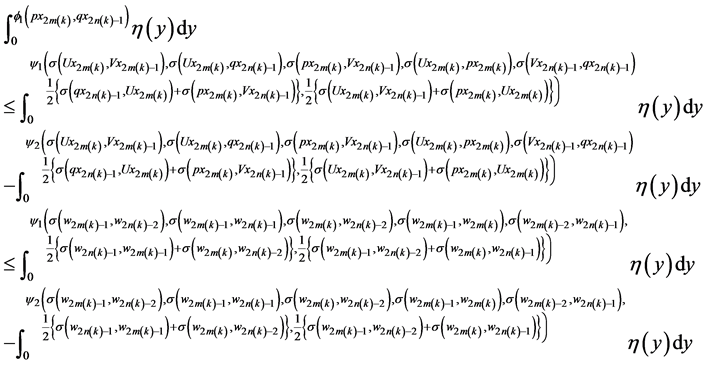
Taking $k\to \infty$ & using (29), (30), (32), (33) & (35) we get

$\begin{array}{c}{\displaystyle {\int }_0^{{\varphi }_1(\in )}\eta \left(y\right)\text{d}y}\le {\displaystyle {\int }_0^{{\psi }_1\left(\in ,\in ,\in ,0,0,\frac{1}{2}\left[\in +\in \right],\frac{1}{2}\in \right)}\eta \left(y\right)\text{d}y}-{\displaystyle {\int }_0^{{\psi }_2\left(\in ,\in ,\in ,0,0,\frac{1}{2}\left[\in +\in \right],\frac{1}{2}\in \right)}\eta \left(y\right)\text{d}y}\\ <{\displaystyle {\int }_0^{{\psi }_1\left(\in ,\in ,\in ,\in ,\in ,\in ,\in \right)}\eta \left(y\right)\text{d}y}={\displaystyle {\int }_0^{{\varphi }_1(\in )}\eta \left(y\right)\text{d}y}.\end{array}$

This is contradiction. Hence $\left\{w_{2n}\right\}$ is a Cauchy sequence and is convergent. Since E is complete there exist $z\in E$ such that as $n\to \infty$ we have $w_n\to z$ .

Case I: Assume that U is continuous then $Up{e}_{2n}\to Uz$ , $U^2{e}_{2n}\to Uz.$ Since (p, U) is sub compatible, we have $pU{e}_{2n}\to Uz.$

Step I: Substituting $s=U{e}_{2n},t=e_{2n+1}$ in (27), we have

$\begin{array}{l}{\displaystyle {\int }_0^{{\varphi }_1\sigma \left(pU{e}_{2n},q{e}_{2n+1}\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{\begin{array}{l}{\psi }_1(\sigma \left(U^2{e}_{2n},V{e}_{2n+1}\right),\sigma \left(U^2{e}_{2n},q{e}_{2n+1}\right),\sigma \left(pU{e}_{2n},V{e}_{2n+1}\right),\sigma \left(U^2{e}_{2n},pU{e}_{2n}\right),\sigma \left(V{e}_{2n+1},q{e}_{2n+1}\right),\\ \frac{1}{2}\left\{\sigma \left(q{e}_{2n+1},U^2{e}_{2n}\right)+\sigma \left(pU{e}_{2n},V{e}_{2n+1}\right)\right\},\frac{1}{2}\left\{\sigma \left(U^2{e}_{2n},V{e}_{2n+1}\right)+\sigma \left(pU{e}_{2n},U^2{e}_{2n}\right)\right\})\end{array}}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{\begin{array}{l}{\psi }_2(\sigma \left(U^2{e}_{2n},V{e}_{2n+1}\right),\sigma \left(U^2{e}_{2n},q{e}_{2n+1}\right),\sigma \left(pU{e}_{2n},V{e}_{2n+1}\right),\sigma \left(U^2{e}_{2n},pU{e}_{2n}\right),\sigma \left(V{e}_{2n+1},q{e}_{2n+1}\right),\\ \frac{1}{2}\left\{\sigma \left(q{e}_{2n+1},U^2{e}_{2n}\right)+\sigma \left(pU{e}_{2n},V{e}_{2n+1}\right)\right\},\frac{1}{2}\left\{\sigma \left(U^2{e}_{2n},V{e}_{2n+1}\right)+\sigma \left(pU{e}_{2n},U^2{e}_{2n}\right)\right\})\end{array}}\eta \left(y\right)\text{d}y},\end{array}$

$\begin{array}{l}{\displaystyle {\int }_0^{{\varphi }_1\left(\sigma \left(Uz,z\right)\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\psi }_1\left(\sigma \left(Uz,z\right),\sigma \left(Uz,z\right),\sigma \left(Uz,z\right),\sigma \left(Uz,Uz\right),\sigma \left(z,z\right),\frac{1}{2}\left\{\sigma \left(z,Uz\right)+\sigma \left(Uz,z\right)\right\},\frac{1}{2}\left\{\sigma \left(Uz,z\right)+\sigma \left(Uz,Uz\right)\right\}\right)}\eta \left(y\right)\text{d}y}\\ -{\displaystyle {\int }_0^{{\psi }_2\left(\sigma \left(Uz,z\right),\sigma \left(Uz,z\right),\sigma \left(Uz,z\right),\sigma \left(Uz,Uz\right),\sigma \left(z,z\right),\frac{1}{2}\left\{\sigma \left(z,Uz\right)+\sigma \left(Uz,z\right)\right\},\frac{1}{2}\left\{\sigma \left(Uz,z\right)+\sigma \left(Uz,Uz\right)\right\}\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\psi }_1\left(\sigma \left(Uz,z\right),\sigma \left(Uz,z\right),\sigma \left(Uz,z\right),0,0,\sigma \left(Uz,z\right),\frac{1}{2}\left\{\sigma \left(Uz,z\right)\right\}\right)}\eta \left(y\right)\text{d}y}\\ \le {\displaystyle {\int }_0^{{\varphi }_1\left(\sigma \left(Uz,z\right)\right)}\eta \left(y\right)\text{d}y}.\end{array}$

It is contradiction if $Uz\ne z$ . Hence $Uz=z.$

Step II: Substituting $s=z,t=e_{2n+1}$ in (27) and taking limit as n tends to infinity we get $pz=z$ .

Step III: We know that $z=pz\in p\left(e\right)\subseteq V\left(e\right)$ then there exist $u\in E$ such that $z=Vu$ . Substituting $s=e_{2n},t=u$ in (27) we get $qz=z$ . Hence $qz=z=Vz$ and $qVu=Vqu$ , which gives $qz=Vz$ .

Step IV: Substituting $s=z,t=z$ in (27) we have $qz=z$ so that $q\left(z\right)=z=Vz$ . Hence p, q, U & V have a common fixed point z in E.

Case II: Assume that U is continuous then $p^2{e}_{2n}\to pz,$ $pU{e}_{2n}\to pz$ . Similarly we can prove that z is common fixed point of p, q, U & V. When q or V is continuous, then the uniqueness of common fixed point follows easily from (27).

Example: Let $E=\left[0,1\right]$ with the usual metric $\sigma \left(s,t\right)=\frac{1}{2}\left|s-t\right|$ . Define $p,q,U,V:E\to E$ such that $ps=\frac{s}{4}$ , $qt=\frac{t}{4}$ , $Us=s$ , $Vt=t$ .

Let ${\psi }_1\left(y_1,y_2,y_3,y_4,y_5,y_6,y_7\right)=\max \left(y_1,y_2,y_3,y_4,y_5,y_6,y_7\right),$ $\phi \left(y\right)=2y$ ,

${\psi }_2=\frac{1}{4}{\psi }_1$ then ${\psi }_1\left(y\right)=y,\forall y\in \left[0,\infty \right)$

$\begin{array}{l}{\left|\frac{s}{4}-\frac{t}{4}\right|}^2\le \frac{1}{4}\max \{\sigma \left(s,t\right),\sigma \left(s,\frac{t}{4}\right),\sigma \left(\frac{s}{4},t\right),\sigma \left(s,\frac{s}{4}\right),\sigma \left(t,\frac{t}{4}\right),\\ \frac{1}{2}\left\{\sigma \left(\frac{t}{4},s\right)+\sigma \left(\frac{s}{4},t\right)\right\},\frac{1}{2}\left\{\sigma \left(s,t\right)+\sigma \left(\frac{s}{4},s\right)\right\}\}\end{array}$

For all $s,t\in E$ , it follows that the condition (27).

Let $\left\{e_n\right\}$ be a sequence in E such that $p{e}_n\to z$ & $U{e}_n\to z$ for some z in E. Then z = 0, $\sigma \left(pU{e}_n,Up{e}_n\right)\to 0$ . Hence $\left\{p,U\right\}$ is sub compatible. We have common fixed point in E.

3. Conclusion

In this paper, we proved the fixed point theorem for four sub compatible maps under a contractive condition of integral type. These results can be extended to any directions and can also be extended to fixed point theory of non-expansive multi-valued mappings.

Acknowledgements

The authors would like to give their sincere thanks to the editor and the anonymous referees for their valuable comments and useful suggestions in improving the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Khan, M.S., Swaleh, M. and Sessa, S. (1984) Fixed Point Theorems by Altering Distances between Two Points. Bulletin of the Australian Mathematical Society, 30, 1-9.
[2]	Aliouche (2006) A Common Fixed Point Theorem for Weakly Compatible Mappings in Symmetric Spaces Satisfying a Contractive Condition of Integral Type. Journal of Mathematical Analysis and Applications, 322, 796-802.
[3]	Babu, G.V.R. (2004) Generalization of Fixed Point Theorems Relating to the Diameter of Orbits by Using a Control Function. Tamkang Journal of Mathematics, 63, 159-168.
[4]	Bouhadjera, H. and Godet, C. (2009) The Common Fixed Point Theorem for a Pair of Sub Compatible Maps. http://hal.archives-ouvertes.fr/hal-00356516v2
[5]	Choudhury, B.S. (2005) A Common Unique Fixed Point Result in Metric Spaces Involving Generalized Altering Distances. Mathematical Communications, 14, 105-110.
[6]	Choudhury, B.S. and Dutta, P.N. (2000) A Unified Fixed Point Result in Metric Spaces Involving a Two Variable Function. Filomat, 14, 43-48.
[7]	Chugh, R. and Kumar, S. (2001) Common Fixed Points for Weakly Compatible Maps. Proceedings of the Indian Academy of Sciences—Mathematical Sciences, 111, 241-247.
[8]	Naidu, S.V.R. (2001) Fixed Point Theorem by Altering Distances. Adv. Math. Sci. Appl., 11, 1-6.
[9]	Sastry, K.P.R., Naidu, S.V.R., Babu, G.V.R. and Naidu, G.A. (2000) The Generalization of Common Fixed Point Theorems for Weakly Commuting Maps by Altering Distances. Tamkang Journal of Mathematics, 31, 243-250.
[10]	Hosseni, V.R. and Hossseni, N. (2012) Common Fixed Point Theorems for Maps Altering Distance under Contractive Condition of Integral Type for Pairs of Sub Compatible Maps. International Journal of Math Analysis, 6, 1123-1130.
[11]	Hosseni, V.R. and Hossseni, N. (2010) Common Fixed Point Theorems by Altering Distance Involving under Contractive Condition of Integral Type. International Mathematical Forum, 5, 1951-1957.
[12]	Wadkar, B.R., Bhardwaj, R.K. and Singh, B. (2014) A Common Fixed Point Theorem in Dislocated Metric Space. International Journal of Engineering Research and Development, 10, 14-17.
[13]	Mishra, L.N., Mishra, V.N., Khatri, K. and Deepmala (2014) On the Trigonometric Approximation of Signals Belonging to Generalized Weighted Lipschitz W(Lr, ξ(t))(r ≥ 1)-class by matrix (C1⋅Np) Operator of Conjugate Series of Its Fourier Series. Applied Mathematics and Computation, 237, 252-263. https://doi.org/10.1016/j.amc.2014.03.085
[14]	Mishra, V.N., Khatri, K. and Mishra, L.N. (2013) Using Linear Operator to Appro-ximate Signal of Lip(α, p), (p ≥ 1)-Class. Filomat, 27, 355-365. https://doi.org/10.2298/FIL1302353M
[15]	Mishra, L.N., Tiwari, S.K., Mishra, V.N. and Khan, I.A. (2015) Unique Fixed Point Theorems for Generalized Contractive Mappings in Partial Metric Spaces. Journal of Function Spaces, 2015, Article ID: 960-827.
[16]	Mishra, L.N., Tiwari, S.K. and Mishra, V.N. (2015) Fixed Point Theorems for Gene-ralized Weakly S-Contractive Mappings in Partial Metric Spaces. Journal of Applied Analysis and Computation, 5, 600-612.
[17]	Deepmala and Pathak, H.K. (2013) A Study on Some Problems on Existence of Solutions for Nonlinear Functional-Integral Equations. Acta Mathematica Scientia, 33, 1305-1313. https://doi.org/10.1016/S0252-9602(13)60083-1
[18]	Wadkar, B.R., Bhardwaj, R. and Singh, B. (2017) Fixed Point Theorems in Dislocated Metric Space. Global Journal of Pure and Applied Mathematics, 13, 2089-2110.
[19]	Wadkar, B.R., Bhardwaj, R., Mishra, V.N. and Singh, B. (2017) Coupled Fixed Point Theorems in Soft Metric and b-Soft Metric Space. Ser. A: Appl. Math. Inform. and Mech., 9, 59-73.
[20]	Wadkar, B.R., Bhardwaj, R., Singh, B. and Mishra, V.N. (2017) Coupled Fixed Point Theorems with Monotone Property in Soft Metric and Soft b-Metric Space. International Journal of Mathematical Analysis, 11, 363-375. http://dx.doi.org/10.12988/7222
[21]	Wadkar, B.R., Bhardwaj, R., Mishra, V.N. and Singh, B. (2016) Fixed Point Results Related to Soft Sets. Australian Journal of Basic and Applied Sciences, 10, 128-137.