1. Introduction
“The fact that the carriers are positively charged is the most important feature which distinguishes high temperature superconductivity from low temperature superconductivity ( [1] , p. 35).”
This fact has long been known and widely acknowledged (e.g. [2] ). The question that remains open is, “What is the superconducting state?” It is generally associated with positively charged “holes”. These holes are unscreened nuclear charges on immobile atoms. The holes are therefore not influenced by the Lorentz force. This acts neither on voids nor on immobile charges; it acts on the electrons. This necessity implies that the Hall coefficient RH should be negative always. A positive RH, whether it is observed in metallic Al, or in p-type semiconductors, or in high temperature superconductors, requires proper explanation. We find it in dispersion dynamics derived from the stable wave packet [3] [4] . Though we start by clarifying the natures of various doped compounds, the logic of this paper is as follows.
The concept of the “hole” (hphys) for the positive Hall coefficient needs modification.
With this concept we answer long standing anomalies including positive coefficients measured in strong metals.
The positive coefficient is a consequence of dispersion dynamics: it is due to negative second derivatives in the energy bands of electronic states that are not completely filled. Similar dispersion occurs in the dynamics of antiparticles [3] [4] .
The dispersion dynamics apply to metals, doped semiconductors, and superconductors.
A weakly related definition for the chemical hole (hchem) is conceptually independent, i.e. an imbalance in ideal local charge in a unit cell, with a superiority of cationic valence over anionic valence. The concept is valid in ionic materials.
In their normal states (T > Tc), high critical temperature superconductors (HiTc1) transport current as holes, hphys with positive RH. By contrast, low critical temperature superconductors (LoTc) transport normal current as free electrons with negative RH.
The chemical hole, hchem, is critical to processing of HiTc compounds. As such it has the same importance as the lattice distortion in the BCS theory of LoTc. It follows that the holes are available in HiTc to bind Bosonic electron pairs.
This pair bonding is principally electrostatic as in compound formation; though there may be a magnetic component since antiferromagnetism typically occurs in compounds overdoped beyond the superconducting phase (e.g. [5] ).
The holes are products both of anionic loading (as in YBCO2, where anionic overloading of a reservoir draws electrons so as to create holes hphys in adjacent superconducting planes) and of mixing with low valence dopants, before solid state reaction as in LBCO3. Sometimes the holes are produced by a planar crystal structure without cationic doping, as in BSCCO4 and TBCCO5; though anionic concentrations are influenced by ambient oxygen pressure during baking.
In dispersion dynamics the superposition of a particle with its antiparticle wave produces a real wave function. We propose that in the HiTc superconducting state, waves of opposite momentum superpose to a real wave function with antinodes on holes, typically arranged at cell boundaries. So long as their temperature is less than critical (T < Tc = εg/kB, the superconducting gap energy divided by the Boltzman constant), the waves transport electric current without resistance. At electrodes, Boson pairs supposedly decompose and reform with net current transport.
The theory for superconductivity provided by Bardeen Cooper and Schreiffer (BCS) depended on the isotope effect: the ratio of critical temperature to isotopic root mass, Tc/MI1/2 = constant [6] . Their theory defined the principal features of low temperature superconductivity in metals and demonstrated the force that binds Cooper pairs, namely a mutual attraction enabled by a lattice distortion. On this attraction depends the second order phase transition; electronic specific heat variations with temperature; the Meissner effect (B = 0); and infinite conductivity (E = 0). The isotope effect is observed only weakly in ceramic superconductors [7] ; instead we have to show how the carrier charges generate and propagate. More recently, new systems have added to our knowledge: the iron pnictides for example; but their Tcs are all lower than the highest in the perovskite and pseudo-perovskite cuprates that were studied in the eventful first eight years of HiTc research. The subsequent added knowledge has not been revolutionary, and attempts to raise Tc have not progressed. However, we now have a clearer demonstration of carrier differences in the LoTc and HiTc ceramics, and we can better interpret the measurements that have been recorded. The superconductive mechanism that is consistent with the prime experimental features is now more obvious than the above quotation describes.
The charge carriers in HiTc superconductors are called “holes”, like those in p-type semiconductors, where the carriers at normal temperatures are also supposed to be positively charged (by simplification; but see below). The “holes” contain two meanings: one defined by chemical composition; the other by physical measurement. Without extrinsic carriers, stoichiometric oxide superconductors ― where the cationic and anionic valencies balance ― ( [1] p. 2) typically, are insulators. However the doping, that is often employed in the ceramic superconductor processing, results in various metallic, superconductive and antiferromagnetic properties [5] . Here, we provide a consistent way for evaluating the charge transport, including the Hall coefficient, through dispersion dynamics in the localized carrier wave function. The investigation has two parts: the first describes chemical composition; the second physical measurement. There is obvious provision for superconducting pair bonding and the corresponding energy gap: the Coulomb force, already responsible in the compound, layered, ionic crystals for chemical hole formation, can also bond superconducting pair charges. At high dopant levels the HiTc compounds transform to non-super- conducting antiferromagnets: the pair bonding may be incidentally assisted by real spin waves and resonating valence bonds [8] or as in related theories [9] [10] [11] .
2. Doping
It is an empirical fact that not all HiTc superconductors are doped (see below); but all contain holes. The doping may be f-type, donating free electrons to the conduction band; or h-type, donating minority holes to the valence band. Hole donation occurs in two ways: cationic and anionic. Substitution of divalent cations for trivalent, causes holes to be formed in the valence band. Conversely, electron donation occurs when cations of higher valence substitute for lower valence. As an anionic dopant, oxygen loading donates holes to the valence band by pulling electrons to an adjacent charge reservoir layer; depletion donates electrons to the conduction band.
In semiconductor physics, the dopants that cause h-type carriers are called p-type, where minority vacancies in a valence band are in thermal equilibrium with nearby p-type impurity states having inferior valence. Free electron f-type carriers in the conduction band of semiconductors are in thermal equilibrium with n-type impurities, having superior valence to the Si matrix. As we show below, the “positive” p-type charge carriers, that operate in the Hall effect, are actually electrons.
The best and most studied example of oxygen loading, YBa2Cu3O7−x (YBCO), is historically the first of the HiTc superconductors to transition above the boiling point of nitrogen. By baking at controlled pressures and temperatures in oxygen or in vacuum, x may range from 0 to 1. In the former case Tc = 93 K falling as the oxygen content decreases ( [1] p. 45). In this system, the superconductivity occurs only when holes are present. In the range 0 < x < 0.5, the excess of oxygen ions forms holes hphys in the electronic band structure. When x = 0.5, ionic charges balance at 13 per unit cell, and the compound does not superconduct. When 0.5 < x < 1, the depletion in oxygen results in f-type charge carriers, at least from a chemical point of view; in Section 4 we discuss their physical measurement.
To view these changes structurally, consider Figure 1 and notice that the HiTc compounds are layered. The figure may be more or less well known, but it is needed here to illustrate the charge reservoir and hole donation in the unit cell of the layered compound. These are important features in the hole exciton that will be discussed later. In the superconducting state with x = 0, the CuO2 atoms
![]()
Figure 1. Crystal structure of YBa2Cu3O7 ( [1] p. 43) showing atomic packing (left) and coordination (right), together with the planar charges on non-equivalent sites in the layered structure. The fractional charges on the CuO2 planes include holes induced by the CuO chains as implied by respective Madelung potentials [12] [13] .
are sandwiched in two planes, each separated on the one side by interspersed Y3+; and on the other by insulating BaO planes. Between the BaO planes lieCuO chains. In the stoichiometric state, with x = 0.5 after baking in a low oxygen ambience, O2− ions become depleted from the chains, making them effectively 1/2[Cu2O] chains. This accompanies a phase transition from orthorhombic to tetragonal. The process is reversible, so that by baking in an atmosphere of oxygen back to x = 0, dissociated O2− ions are absorbed into the chains and draw electrons from the CuO2-Y-CuO2 planar complex where holes are created. This fact is illustrated by calculations on Madelung potentials [12] [13] [14] 6. In these calculations, charges must balance across a unit cell as indicated at the right of Figure 1; however in practice the fractional charges on the CuO2 planes are in principle integral and are balanced by the h+ hole in the superconducting layer. Here the charges balance when Y3+ + h+ provide 4 positive charges that balance the 4 negative charges on the two [CuO2]2− planes. The hole is an excess of nuclear charge at the valence band. The chief evidence is of course the positive Hall coefficients measured at T > Tc due to normal currents. Baking in vacuum all the way to x = 1, the reversal depletes the chains of all O and releases electrons into the conduction band of the system. The chains therefore serve as charge reservoirs that create lattice holes for superconductivity, especially when x ~ 0. When T > Tc, the holes are instrumental in the positive Hall coefficient (see below); but on cooling to T < Tc, they are available to bind Cooper pairs for superconducting transmission.
YBCO is an example of a ceramic superconductor in which the doping is reversible. Doping that occurs during solid state reaction is reversible only in the anionic composition. An example is the first discovered HiTc superconductor, Ba doped La2CuO8, or LBCO. This compound has been compared elsewhere [1] with BSCCO and with TBCCO neither of which contain cationic doping: the holes are a product of the layered crystal structure. Of these, the former is illustrated in Figure 2, showing three forms with n = 0, 1 and 2. They have Tc = 10 K, 80 K and 110 K respectively. For the last, the charge structure in reservoir and hole layers is indicated at the right. For Madelung potential calculations, the positive and negative ionic charges must balance across the unit cell as shown. However, electrons attracted to the [BiO]+ layers leave two holes in the cuprate region: the 6 ionic charges on [CuO2]− are balanced by 2Ca2+ + 2h+. The Fermi level is adjusted, and this determines the energy of the hole states in the conduction band. (It is in principle possible to measure the Fermi level by ionization of core excitons in soft X-ray spectroscopy [13] [15] but the same difficulties arise as in photoelectron spectroscopy where various atomic sites, especially of Cu, give mixed signals.)
In contrast to the minor structural changes in oxygen loaded YBCO where the hole layer, within the CuO2 planes, is relatively thin; BSCCO demonstrates the
![]()
Figure 2. (a) Atomic packing of BSCCO; (b) crystal structures of Bi2Sr2CanCun+1O6+2n, with n = 0, 1 and 2 showing coordination. At right, planar charges show non-equivalent sites with n = 2.
importance of structure in the hole layers, since Tc depends strongly on how thick these layers are, i.e. increasing with n. The similar TBCCO system, TlBa2Can−1CunO2n+2, likewise shows an increase in Tc from 10 K to 78, 120 and 121 K, when n = 1, 2, 3 or 4 respectively; but falls away to 105 K when n = 5 ( [1] , p. 48). So in this system there is an optimum thickness for the hole layer complex. The critical temperature in YBCO is typical for a cuprate HiTc structure with n = 2. The composition of reservoir layers has significant but less dramatic effect on the magnitudes of Tc. The same trends are seen in members of the A2B2CanCun+1O6+2n system, given elsewhere [1] . The detailed dependence of the superconducting energy gap εg on either the oxygen loading or on the structure of the hole layer complex are still unclear; but there can be little doubt that the distribution of charge across the unit cell is fundamental in the formation of superconducting Boson pairs. The distribution is subsidiary to the prior crystal structure of the multi-layered cuprates.
In BSCCO, the holes were formed without doping, though ambient oxygen pressure is controlled in baking. Maple [5] has described two systems with similar crystal structures: Nd2−xCexCuO4−y is electron doped, since Ce has higher valence than Nd (like n-type Si doped with P); while La2−xSrxCuO4−y is hole doped since Sr has lower valence than La (like p-type Si doped with B). The former is a free electron, f-type superconductor; the latter a hole, h-type. At optimum doping, Nd2−xCexCuO4−y is a low temperature superconductor with Tc = ~25 K, at x = 0.15, and RH < 0; while La2−xSrxCuO4−y is a high temperature superconductor with Tc = ~40 K, at x = 0.18, with RH > 0. Both systems exhibit antiferromagnetic phases at high x, while the hole doped system has an extra spin glass phase between 0.02 < x < 0.06. Above the latter value, superconductivity sets in at low temperatures. With this difference in the spin glass, the phase diagram of the first compound, plotted against abscissae x, is a distorted image of the phases in the second.
The highest Tc repeatedly found in the ceramic superconductors is 133 K in HgBa2Can−1CunO2n+2. This is a member of a group of systems where n can vary: n = 1, 2, 3 or 4. As n decreases Tc declines. As in BSCCO, the copper planes are adjacent, so it appears again that the packing together of CuO2 planes contributes actively to the superconducting pair energy gap. Next we consider how the chemistry that we have described influences energy bands for the valence and conduction electrons.
3. Hubbard Bands, Valence and Madelung Potentials
The superconducting compounds that have the highest Tcs and that have been best studied are cuprates [1] [2] . Consider this group in particular, though the general features apply more widely. Cu is a 3d transition metal, typically divalent but sometimes monovalent. The 3d bands fall into two Hubbard bands: filled and unfilled. Suppose that, in the non-superconducting YBCO compound with x = 0.5, the valence band has anionic character, separating the Hubbard bands. After the phase transition that accompanies x → 0 in YBCO, the consistently valued Madelung potentials [12, table I, columns 3 and 5: fractional charges ensure computational convergence at large distance] imply holes in the CuO2 planes, lowering the energies of the anionic bands and raising the energy of the Hubbard bands as in La2−xBaxCuO4−y ( [1] , p. 66). The Madelung potentials are consistent when the energy levels ― determined by 1) the Madelung potentials, and 2) ionization energies on cations, and 3) electron affinities on anions ― are similar for all members on the same ionic species in the unit cell. Some allowance must be made for hole planes or reservoirs. Since the model depends on fine atomic states, and does not account for the band spread that is due to crystal fields, the valence to conduction band gaps are often double those measured by the energy of the fundamental absorption.
In YBCO, the oxygen loading acts as a charge reservoir that adjusts the Madelung energies of the atoms in the planes, and also adjusts the Fermi level. The loading sets the environment for holes in the valence band-and therefore for h-type Boson carriers at T < Tc. (In former times, Madelung potentials were calculated analytically; but more versatile calculations can now, after careful checks for convergence, be performed numerically.)
The valence bands can in principle be investigated experimentally by microprobe angularly resolved electron photo-emission (μARPES). Kondo et al. [16] , for example, observed two dimensional (2D) bands in the planes and quasi one dimensional bands (1D) on the chains. The conduction electrons were well confined within the planes and chains with non-trivial hybridization. As we shall see, interpretation of such data will be enhanced by scanning over various photoelectron energies to find the dispersion in frequency space. The same consideration applies to electron energy band structure calculations, though they are difficult when unit cells are large and diverse. However, localized band structures, such as those calculated by Hu et al. for Cu when octahedrally coordinated to O [17] , provide useful but limited information about dispersion derivatives and band gaps.
ARPES has also been used to map Fermi surfaces. In well doped YBCO, the surfaces are cylindrical; in underdoped specimens the surfaces are closed pockets [2] [18] .
Meanwhile, carrier densities are measured by the Hall effect, so it is worth discovering whether its measurement in the superconductors correlates with their chemical environment. Unfortunately the firm chemical perspective is not equally complemented by comparatively weak physical characterization [1] [19] [20] [21] . The discrepancy is partly theoretical (as below). Even so, the Hall effect in HiTc compounds can often be interpreted on elementary models in a more or less predictable way as for example in HgBa2CaCu2O6+δ [22] and even YBCO [23] ; more debatable are the systems which can be processed to have either free electron carriers or hole based carriers, and which we therefore discuss in following sections.
4. The Hall Effect and Its Dependence on Crystal Energy-Band Dispersion
Since, in the superconducting state, the electric field, E = 0, and the magnetic force field, B = 07 are both zero, we have to identify the charge carriers in the normal state, either at elevated temperatures above the critical temperature, T > Tc, or in strong magnetic fields above the critical induction field H > Hc(T). On cooling to Tc, the Fermionic normal state carriers are presumed to condense to the Bosonic superconducting state. As mentioned earlier, in low temperature superconductors, the carriers are negatively charged and have negative Hall coefficients that are measured in the normal state; the HiTc superconductors have positive Hall coefficients. The coefficient measures the cross voltage resulting from an electric field Ez that is generated when a current density jx = σEx is made to pass through a magnetic field By [24] :
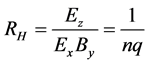 (1)
(1)
where in introductory texts, Hall measurements are simply described: suppose that the carriers act as free particles. An electric field E is applied across a conductor. Let it be vertically upwards E = Ex. The carriers are accelerated and are scattered by collisions with the lattice to achieve a mean current density, j = nvq, where n is the carrier density, v the drift velocity, while the carrier charge q = ±e, and −|e| is the electronic charge. Positive charges are forced parallel to Ex; negative charges anti-parallel. A magnetic force field B = By is applied normal to E. The carriers are diverted by the Lorentz force and so tend to the same z direction where charge buildup causes a cross field qEz = qvxBy. In the steady state, jz = 0. Then the Hall coefficient can be defined as in Equation (1). RH is negative for electrons and positive for holes. Many objections can be raised to this over-sim- plified explanation. In order to interpret the published Hall effect data on high temperature superconductors, we will consider one show stopper first, and then two criticisms. The solution follows our prior treatment of dynamics in localized particles and antiparticles [3] [4] .
The principle objection to be considered is that the hole is not a particle: the Lorentz force does not act on voids, nor does it act on immobile nuclear charges. The hole “carrier” was supposed to be a vacancy in an otherwise filled band of states. The states are derived from fine atomic-like states that are dispersed in energy by a crystal lattice potential. The hole vacancy was supposed to act like a particle. How? The solution we propose for the phenomena that involve the positive Hall coefficient in an environment of negative charges, lies not in quantum mechanics; but in classical wave mechanics (Appendix). The positively charged, immobile ions, that resistively scatter electrons in the HiTc compounds, do not contribute to the Hall coefficient, because the ions transport electric current at neither normal nor low temperatures.
To understand the transport, follow a) Plank’s law, b) the de Broglie hypothesis and c) Maxwellian electromagnetism, and assume the particles travel in wave packets. The simplest packet that describes the physics of the transport is Gaussian [3] [4] . Following Dirac, the wave packet is generally supposed unstable; however, the traveling wave group for a free particle or photon:
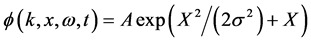
with
 (2)
(2)
is defined on values of mean wave vector k and mean angular frequency ω. The equations are perfectly stable on a wide transverse wave, not only because k and ω are mean values in a symmetric wave function; but their stability is guaranteed by respective conservation of momentum and energy; and triple guaranteed by symmetry in space-time. Equation (2) is given in simplified units for Planck’s constant and the speed of light
= c = 1. In the direction of propagation, X is imaginary causing 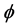 to oscillate. If the real part represents the electric field in an electromagnetic wave, the imaginary part represents the relative phase of its (real) magnetic force field. The denominator is particular because it depends on initial conditions, but it is stable during propagation in free space as a consequence of Newton’s first law of motion. The coherence σ describes the width of the packet in either space or time. The normalizing amplitude A depends on σ and has corresponding stability. The envelope, exp(X2/2σ2), depends on the square of imaginary X, itself a function of four variables. Two are already described, so we are left with the variables x and t that describe the profile. Since the other variables are all stable, this profile is also stable. With a stable wave group, we can progress to new physics. Apply this packet to approximately free particles in (d) Einstein’s formula for special relativity. Then either by direct substitution of (a) and (b) in (d), or by operation of the relativistic Klein Gordon equation on the Gaussian wave packet, derive the formula for a free particle:
to oscillate. If the real part represents the electric field in an electromagnetic wave, the imaginary part represents the relative phase of its (real) magnetic force field. The denominator is particular because it depends on initial conditions, but it is stable during propagation in free space as a consequence of Newton’s first law of motion. The coherence σ describes the width of the packet in either space or time. The normalizing amplitude A depends on σ and has corresponding stability. The envelope, exp(X2/2σ2), depends on the square of imaginary X, itself a function of four variables. Two are already described, so we are left with the variables x and t that describe the profile. Since the other variables are all stable, this profile is also stable. With a stable wave group, we can progress to new physics. Apply this packet to approximately free particles in (d) Einstein’s formula for special relativity. Then either by direct substitution of (a) and (b) in (d), or by operation of the relativistic Klein Gordon equation on the Gaussian wave packet, derive the formula for a free particle:
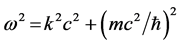 (3)
(3)
where m is the rest mass. Differentiate (2) to find
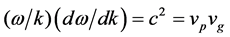 (4)
(4)
i.e. the product of the phase velocity and group velocity. From this follow many consequences including negative mass when the second derivative of the dispersion is negative, i.e.
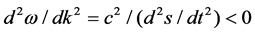 (5)
(5)
[3] [4] [25] , where s marks the central location of beating waves. Equations (2)-(4) are the fundamental equations of dispersion dynamics. From these are derived the formula for a free antiparticle, with negative mass, frequency and wave vector; but having positive group and phase velocities. Then, with m < 0 in a positive force field, Newton’s second law of motion is satisfied. The effective mass is the force f required to produce unit acceleration in the central location of beating waves of a particle, which is also the maximum of a wave packet in space.
These dynamics for antiparticles are derived from relativity, but they can be applied to carriers in semiconductors when the dispersion of valence or conduction bands, due to periodic crystal potentials, is independently calculated. The electron energy bands in the solid substitute for dispersion due to kinetic energy in free particles. In silicon for example, the top of the valence band disperses electrons with negative second derivative. The carriers in such states have negative mass [26] 8 and negative charge, but positive group and phase velocities [3] [4] . At the top of the valence band containing vacant hole sites, electrons act as if positively charged with positive mass, and respond to Coulomb or Lorentz forces accordingly; though this description is only apparent; not causal. The dynamics of hole bound electrons mimic those of antiparticles when they have negative second derivatives in dispersion. The fact of positive Hall coefficients in p-type semiconductors is evidence not for positive charge on the void nor for positive nuclear charges that are immobile; but for dispersion dependent, negative mass on the most energetic valence electrons. The cooling effect of negative motion in the electric field counteracts Ohmic heating at electron collisions with the crystal lattice.
This understanding of the Hall effect in p-type semiconductors brings a second embarrassment―one that would be called a second show stopper if it had not failed to lower the curtain so often in the past. Several metals, including one of the most conductive, namely Al, have positive Hall coefficients [24] , even though there is no doubt that the carriers are negatively charged electrons. The solution again lies in the band structure, examples of which can be found in the literature. Al is a light metal, and while its electrons are sometimes described as free electron-like by comparison with transition metals; in fact the band structure of the [Ne]3s23p based atomic states shows some complexity. There are, in the valence band, dispersive peaks with negative second derivatives. Further study is needed to match these peaks to experimentally measured Hall coefficients, but it is reasonable to expect this can be done.
A third criticism derives from complications that arise in strong magnetic fields: the free paths between scattering collisions cease to be approximately linear and tend toward circular resonance. This affects magneto-resistance and stimulates important information on Fermi surfaces in metals. The foregoing analysis is a weak field approximation.
Apply now the understanding, just described, to the Hall coefficients and resistive data in YBCO measured by Wuyts et al. [18] . Their specimens were thin films, which typically have lower Tcs than bulk specimens, among other characteristic properties that are often different. Nevertheless, electrical contacts can be made more reliably on thin film specimens than on bulk ceramics and this reflects on experimental reliability. The authors report two sets of temperature dependent resistivity data, with x < 0.5 and x > 0.5, that fell on two straight lines with a change of slope where x = 0.5 the stoichiometric value. This is consistent with different carrier types above or below stoichiometry. Moreover their Hall measurements ranged between temperatures T = 100 K to 300 K. At these temperatures, T > Tc, a component of the resistivities and Hall coefficients respond to holes when x < 0.5 and to free electrons otherwise. However, as with Al, the f-type electrons may suffer negative second derivative in dispersion and so can have positive RH. Its sign depends in the curvature of the conduction band.
Notice that though YBCO is superconducting at low temperatures when it is loaded with oxygen, it is otherwise weakly metallic. It is well known that the temperature dependence of the normal resistivity does not follow Drude behavior: pure superconductors that are optimally loaded, show resistance that is linear with temperature, but cut off at temperatures below Tc, so that ρ (T < Tc) = 0. An imaginary extension of the linearly resistive behavior to lowest temperatures cuts through the origin, ρn(T = 0) ~ 0. When x ≥ 0.5, the compound is likewise weakly metallic owing to the f-type electrons; but does not superconduct.
The measured Hall coefficients were positive both in the set with x<0.5 and with x > 0.5. In Figure 3 we re-plot n(RH(x))-n(RH(0.5)) from the data of Wuyts et al. Following equation 1, the intrinsic (stoichiometric) carrier density is measured at x = 0.5, and since it is subtracted in the modified coefficient n(RH) in the figure, the value there is zero. More generally, there is a rough inversion symmetry in the figure between the regions 0.3 < x < 0.5 with 0.7 > x > 0.5 and this is what we expect. The fact that RH is positive when x > 0.5, with f-type electrons, is not an inconsistency: the sign on the coefficient depends on the dispersion of conduction bands. If these exist in pockets, as measured by ARPES in lowly doped YBCO [2] [18] , then it is not surprising to find the positive RH.
![]()
![]()
Figure 3. Re-plotted values of Hall carrier densities in thin film YBa2Cu3O7−x versus x, extracted from the thin film data of Wuyts et al. [18] . Their data are all positive for x < 0.5 to x > 0.5, so we have subtracted an intrinsic component n(x = 0.5) at the stoichiometric condition, the cross from h-type carriers to f-type carriers. Despite a discontinuous slope in resistivity there is a rough inversion symmetry about x = 0.5.
5. Excitonic Wave Packets
With the dynamics described, we can reinterpret Hall data. It is obvious that the HiTc compounds owe their superconducting properties to chemical holes. A first hypothesis is that charge is transported in superconductivity by localized wave packets such as the Gaussian traveling wave group. The packets are subject to typical dynamics for particles and antiparticles. The holes are formed in valence bands with negative second derivatives in the dispersion. Valence electrons have negative mass and negative charge that respond to applied Lorentz forces. At low temperatures, the holes bond Cooper pairs, or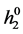 , with two electrons having, as in the BCS theory, opposite momenta. The superposed wave function is real, with singlet spin S = 0. The real wave function synchronizes with the crystal lattice and forms a bound exciton, h− or
, with two electrons having, as in the BCS theory, opposite momenta. The superposed wave function is real, with singlet spin S = 0. The real wave function synchronizes with the crystal lattice and forms a bound exciton, h− or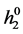 . The former is a negatively charged hydrogen-like ion, but extended in space over its known coherence length, 2.7 nm ( [1] , p. 21); the latter alternative has neutral charge. We propose that, as the instrument for Cooper pair formation, the exciton in HiTc replaces the BCS lattice distortion in Nb. We can compare the wave packet with either an H− ion, or with neutral H2
. The former is a negatively charged hydrogen-like ion, but extended in space over its known coherence length, 2.7 nm ( [1] , p. 21); the latter alternative has neutral charge. We propose that, as the instrument for Cooper pair formation, the exciton in HiTc replaces the BCS lattice distortion in Nb. We can compare the wave packet with either an H− ion, or with neutral H2
The electron affinity of the neutral hydrogen atom is 0.754 eV [27] ; the exciton, being dispersed over a larger area should have an affinity some fraction of this number. At the critical temperature of 133 K, the energy is predicted from the Boltzmann constant to be 11 meV. This becomes the energy gap for pair bonding in the exciton model for HiTc superconductivity. The positive charges in the excitons form a sea ( )r of charge sites induced by the chemical charge distribution in the planar HiTc superconductor. This distribution is a product of the doping described in Section 2. The sea is implied by the cooperative carrier charge behavior that is observed in Josephson junctions [28] . Conservation of energy, prohibits the breaking of these pairs at low temperatures, and therefore prohibits also resistive scattering in the superconductors. The
)r of charge sites induced by the chemical charge distribution in the planar HiTc superconductor. This distribution is a product of the doping described in Section 2. The sea is implied by the cooperative carrier charge behavior that is observed in Josephson junctions [28] . Conservation of energy, prohibits the breaking of these pairs at low temperatures, and therefore prohibits also resistive scattering in the superconductors. The  excitons are not required to accelerate in electric fields; only to dissociate at normal electrodes. Charge transport occurs when a wave packet decomposes at one normal (positive) electrode by releasing an electron, and re-forms in Newtonian time [3] [4] at the opposite (negative) electrode. The electric acceleration of alternative h− excitons is straightforward.
excitons are not required to accelerate in electric fields; only to dissociate at normal electrodes. Charge transport occurs when a wave packet decomposes at one normal (positive) electrode by releasing an electron, and re-forms in Newtonian time [3] [4] at the opposite (negative) electrode. The electric acceleration of alternative h− excitons is straightforward.
Excitons take many forms [29] . They may be localized or extended in waves. They may be stationary or mobile. In intrinsic semiconductors a conduction electron can be bound to a hole in the valence band, with common group velocity. Silicon, for example, has an indirect band gap, so that the excited state has a comparatively long life time. Hydrogenic series of excitonic states are detected in the energy gap between the conduction and valence bands. The binding energies of “positronium” are in the millivolt range ( [24] p. 333). Core excitons have larger binding energies, tens of volts. They are observed in vacuum ultraviolet and electron spectroscopies, especially in ionic solids. The states are atomic excited states that ionize at the conduction band [13] [15] . They otherwise follow ― in reflection [13] and electron excitation [30] spectroscopies of solids ― normal selection rules for atomic spectra. The excitons that we find in HiTc compounds differ from those in Si because the positive charge in the former is provided by a chemical hole, i.e. induced by the reservoir layer, during processing. Since the pair bonding shares chemistry with hole states h+ and with excitonic hole states h0, the pairing is empirically based. Incidentally, the proposed functionality of the hole in HiTc superconductivity can be seen to fill a gap in the explanation for Cooper pairing in the BCS theory.
Can HiTc be extended to room temperature? Dispersion dynamics suggest that one route to higher Tcs is through engineering of valence bands to higher dispersion curvature. A second route is the obvious one that has not borne fruit over twenty years, namely variations on the structure and composition of HgBa2Can−1CunO2n+2. When n = 4 the multi-layer hole complex produced maximum Tc. It is interesting to speculate on whether epitaxial film growth could provide a release from crystal constraints and provide opportunity for electron energy band structures that induce larger superconducting band gaps εg, perhaps linear, rather than planar or 3-dimensional.
6. Conclusion
In the Hall effect, the Lorentz force cannot act on voids or immobile nuclear charges; it must act on electrons whose effective mass, positive or negative, depends on dispersion dynamics. Electrical transport, in the normal state and in the superconducting state, poses two separate problems. However, the obvious importance of chemical holes in the structure and its correlation with electrical properties, implies that the evident holes are available to form excitons in the normal state when T > Tc. Then condensation can occur by pairing of excitons, when temperatures are sufficiently low. This mechanism is the alternative in HiTc to the lattice distortion that facilitates low temperature superconductivity in the BCS theory for metals. However, the chemical hole has further effects. It lowers the energies of anionic bands relative to the cationic bands, radically changing the dispersion near the Fermi surface. Materials that are magnetic or superconductive are mutually exclusive; but high doping often transforms the superconducting phase into an antiferromagnetic one. The hole-based exciton is a more obvious alternative to the antiferromagnetic pair bonding that is often proposed in HiTc theory.
Appendix: What Is Quantization and When Is It Useful?
Clarity requires that wave mechanics be distinguished from quantum mechanics, not only in the description of the Hall Effect, but generally in physics [3] [4] [31] [32] [33] 9. The prior wave mechanics was developed by Huygens, Fraunhofer, Fresnel and others. Their theories provided probability methods in the wave theory of light, including interference, focusing with zone plates, etc. Subsequently, Maxwell’s theory of electromagnetism provided for the energy of a wave packet. Planck’s law showed that, in atomic emission and absorption spectra―and also in the photoelectric effect due to those emissions―energy is quantized. The law gave us Planck’s constant, the energy of a quantum on the extreme right of the following equation:
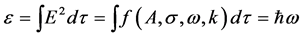 (A.1)
(A.1)
where E is the electromagnetic electric field vector; and f is a function of A, the amplitude integrated over space. The coherence and amplitude describe the physical properties of localization that are hidden in the Copenhagen interpretation of quantum mechanics. The simplest wave packet was described in Equation (2). The de Broglie hypothesis showed a corresponding result for wavelength and momentum that was demonstrated experimentally. The probability theories were thus extended to particle behavior.
More precisely in the atom, quantization is the consequence of standing waves in the Bohr atom and in the Schroedinger equation. Resonance imposes space- time limitations on the orbits of moving particles because unquantized “resonances” would self destruct or decompose as unobservables. In observables, mathematical solutions to the space-time limitations provide resonant eigenvalues in energy or momentum. The quantization is generally due to confinement of states in space and time, and must be evident in either emission or absorption of those states. The energy of the wave packet, which was undetermined in Maxwell’s theory, is determined by the resonant confinement of complex waves.
Thus, in emission spectra of atoms, photon energies are quantized by the initial and final eigenvalues for the Hamiltonian on the emitting atom. In line absorption, the corresponding eigenstates are found in the absorbing atom. These states quantize the energies of photons observed.
This is the beginning however: quantum mechanics describes distinguishable and indistinguishable particles that obey different statistics, again owing to their peculiar conditions for overlapping wave functions. The former type allows Bose-Einstein condensates for distinguishable particles; the latter satisfy Pauli exclusion and Fermi-Dirac statistics for indistinguishable particles. The former describe superconductivity; the latter normal electrical conductivity. The space- time conditions for resonance and superposition are different in the two cases, with integral or half-integral spins respectively. Further consequences are boundless.
In particular, creation and annihilation operators, with alternative corresponding conditions for operator commutators, were made to substitute for amplitude and coherence. The computational effort is thus frequently simplified. The effort bypasses localization that is properly described by wave mechanics and that is employed in this paper.

Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmp@scirp.org
NOTES
![]()
1Tc is the critical superconducting temperature. It is not confused with the Curie temperature which is not discussed in this paper.
2YBCO: YBa2Cu3O7−x.
3LBCO: La2−xBaxCuO4-y; La2-xSrxCuO4-y is a similar compound.
4BSCCO: Bi2Sr2CanCun+1O6+2n.
5TBCCO: TlBa2Can−1CunO2n+2.
![]()
6In ref. [9] , Table 1, columns 3 and 5, the consistency of the numbers demonstrate positive “hole” charges (electron energy band vacancies) on the CuO2 planes. For a fuller interpretation, the Madelung potentials are supplemented by work functions and electron affinities as described there and elsewhere [12] [13] .
![]()
7There is local penetration in type II superconductors including the high temperature superconductors.
![]()
8These authors reached the same conclusion of negative mass on the constrained electron, but by a different route.
![]()
9Because Heisenberg’s axiom is unquestionable in mathematics, it is meaningless in physics besides being redundant. It is wrong in engineering by at least an order of magnitude [3] [4] [24] [33] [34] [35] .