Image Retrieval Using Deep Convolutional Neural Networks and Regularized Locality Preserving Indexing Strategy ()
1. Introduction
Indeed, how to dig out the potential information contained in these features is another critical issue. We believe that there is a certain internal structural link between similar features. Thus, our main purpose is to find out this link and RLPI is a good choice in helping us with this research [2]. RLPI is fundamentally based on LPI which is proposed to find out the discriminative inner structure of the document space. However, in out paper, we apply it to the image feature space and get a good performance.
2. Method
2.1. VGG-Net
Many studies demonstrate that deeper networks can achieve better performance. However, training deeper networks not only dramatically increases the computational requirements but also needs stringent hardware support. In our work, we utilize VGG-net model to extract image features. In order to implement this network with moderate computing requirements, each image is re- scaled to the same size of 224 × 224, which is then represented with a vector of 4096 in dimension in terms of the network after removing the FC-layer.
2.2. A Brief Review of LPI and RLPI
2.2.1. Locality Preserving Indexing
LPI is proposed to find out the discriminative inner structure of the document space and extract the most discriminative features hidden in the data space. Given a set of data points and a similarity matrix. Then LPI can be obtained through solving the following minimization problem:
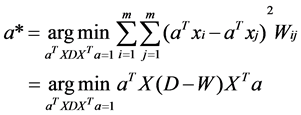 (1)
(1)
where  is a diagonal matrix and its entries are column sums of
is a diagonal matrix and its entries are column sums of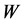 . The
. The 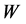 can be constructed as:
can be constructed as:
 (2)
(2)
where  is a set of
is a set of 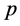 nearest neighbors of
nearest neighbors of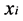 .
.
As the objective function will generate a heavy penalty if neighboring data points 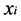 and
and 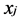 are mapped far apart. Thus, to get the objective function minimization is an attempt to ensure that if
are mapped far apart. Thus, to get the objective function minimization is an attempt to ensure that if  and
and 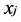 are close then
are close then  and
and 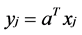 are close as well [3]. Then, the basis function of LPI are the eigenvectors associated with the smallest eigenvalues of the following generalized eigen- problem:
are close as well [3]. Then, the basis function of LPI are the eigenvectors associated with the smallest eigenvalues of the following generalized eigen- problem:
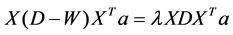 (3)
(3)
Thus, the minimization problem in Equation (1) can be changed to the following problem:
 (4)
(4)
and the optimal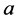 ’s are also the maximum eigenvectors of eigen-problem:
’s are also the maximum eigenvectors of eigen-problem:
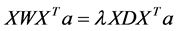 (5)
(5)
However, according to [2], the high computational cost limits the application of LPI on large datasets. RLPI aims to solve this drawback through solving the eigen-problem in Equation (5) efficiently.
2.2.2. Regularized Locality Preserving Indexing
The following theorem can be used to solve the eigen-problem in Equation (5) efficiently:
Let ![]() be the eigenvector of eigen-problem:
be the eigenvector of eigen-problem:
![]() (6)
(6)
with eigenvalue![]() . If
. If![]() , and
, and ![]() is the eigenvector of eigen-problem in Equation (5) with the same eigenvalue
is the eigenvector of eigen-problem in Equation (5) with the same eigenvalue ![]() [2].
[2].
Based on this theorem, the direct computation of the eigen-problem in Equation (5) can be avoided and the LPI basis function can be acquired through the following two steps:
1) Solve the eigen-problem in Equation (6) to get![]() .
.
2) Find ![]() which can satisfy the equation
which can satisfy the equation ![]() and a possible method to find
and a possible method to find ![]() which can best fit the following equation in the least squares sense:
which can best fit the following equation in the least squares sense:
![]() (7)
(7)
where ![]() is the
is the ![]() -th element of
-th element of![]() . A penalty can be imposed on the norm of
. A penalty can be imposed on the norm of ![]() to avoid infinite many solutions for the linear equations system
to avoid infinite many solutions for the linear equations system ![]() through the following method:
through the following method:
![]() (8)
(8)
where ![]() is a parameter to control the amounts of shrinkage. This is the regularization which can be well studied in [4]. Thus, we called this method as Regularized Locality Preserving Indexing (RLPI). Let
is a parameter to control the amounts of shrinkage. This is the regularization which can be well studied in [4]. Thus, we called this method as Regularized Locality Preserving Indexing (RLPI). Let![]() , and the RLPI embedding is as follows:
, and the RLPI embedding is as follows:
![]()
where ![]() is a
is a ![]() -dimensional new representation of the image
-dimensional new representation of the image ![]() and this is our main purpose. From this point of view, RLPI is also a dimensionality reduction method.
and this is our main purpose. From this point of view, RLPI is also a dimensionality reduction method. ![]() is the transformation matrix. When we perform image retrieval, we can use this new feature representation to retrieval the similar images in the database through cosine distance.
is the transformation matrix. When we perform image retrieval, we can use this new feature representation to retrieval the similar images in the database through cosine distance.
3. Experiments Results
In order to evaluate the performance of our proposed method, experiments are conducted on Caltech-256 dataset. For the purpose of comparisons, results from other methods are also presented.
3.1. Image Datasets
Caltech-256 dataset contains 29780 images in 256 categories. We select images from the first 70 classes of the caltech-256 dataset to construct a smaller dataset (referred to as Caltch-70 here and after) consisting of 7674 images for our experiment. We select 500 images randomly as the queries and the remaining as the targets for search.
3.2. Quantitative Evaluation
Three measures are used to evaluate the performance of different algorithms. The first one is the precision defined as:
![]() (9)
(9)
where ![]() is the number of correct relevant returns among the
is the number of correct relevant returns among the ![]() retrieved images.
retrieved images.
The precision tells us the rate of relevant images in total retrieved images in a particular search. However, sometimes, we want to get more relevant images from the database rather than just a very high precision. Thus, the recall is also an important measure of the performance of different algorithms. We define the second measure recall as:
![]() (10)
(10)
where ![]() is the total number of relevant images in the dataset.
is the total number of relevant images in the dataset.
3.3. Results
A. Comparisons with Hash Type Methods
In this section, we compare our proposed method (VGG-RLPI) with many hash type methods [5] [6] [7]. In [6], Iterative Quantization (ITQ) and PCA random rotation (PCA-RR) methods are proposed which represents state-of-art in 2013. And many classic hash type methods such as locality sensitive hashing (LSH), PCA hash (PCAH) and SKLSH [7] are also in comparison with our proposed method and from the results, we can find that our proposed method is superior to these methods.
Figure 1 shows the retrieval precision and recall of different methods averaged among 500 queries in the Caltech-70 dataset. For the purpose of comparisons, results from other hash type methods are also presented. In these methods, features are extracted with the VGG-net. From the curves in this figure we can see that our proposed method (VGG-RLPI) performs the best among others.
B. Comparisons with Dimension Reduction Methods
As has mentioned above, the RLPI is also a dimension reduction method. Thus, comparisons are also performed with two other dimension reduction methods: the Principle Component Analysis (PCA) method and the Linear Graph Embedding (LGE) method. For fair comparisons, retrieval experiments are first performed with reduced feature vectors obtained from these three methods to determine the optimal dimension. Figure 2 gives the mean precision of the three methods at different number of returns in the Caltech-70 dataset. From the figure, we can see that the optimal dimension is 100 both for LGE and RLPI. However, for PCA method, the curves almost coincide when feature dimension exceed 50. Thus, for the following comparison, we select the precision corresponding to 100 dimension for the three dimension reduction methods. From the results in Figure 3 we can find that our proposed method superior to the other two ones.
4. Conclusion
![]()
![]() (a) (b)
(a) (b)
Figure 1. Image retrieval results: (a) Precision of Image Retrieval on Caltech-70 dataset; (b) recall of Image Retrieval on Caltech-70 dataset.
![]() (a)
(a)![]()
![]() (b) (c)
(b) (c)
Figure 2. Mean retrieval precision with reduced feature vectors from two dimension reduction methods: (a) PCA method and (b) LGE method and (c) RLPI method.
![]()
![]() (a) (b)
(a) (b)
Figure 3. Comparison of VGG-RLPI and dimension reduction methods with optimal dimension in the Caltech-70 dataset: (a) Mean retrieval precision; (b) mean retrieval recall.
more discriminative compare to the original features. Experiments results in the Caltech-70 datasets show that our proposed method outperforms existing hash based methods and two other popular dimension reduction methods.