1. Introduction
Flash flooding in the
UK
has been a major cause of water related deaths during the 20th century. The worst of these events was the Lynmouth flood disaster in which 34 people were drowned in 1952. This is followed by the Louth flood of 1920 in which 23 souls were lost. More recently people have been drowned during the floods of 1958 (Boscastle), 1968 (Mendip), 1998 (
Midlands
), 2007, 2009 and 2012. For those who survive such ordeals the psychological effects can be dramatic [1]. Having suffered such losses in the past the authorities have been woefully slow to provide good quality flood warnings. Sene [2] provides an overview of the methods used to warn people of serious flooding. The requirements for warnings include rainfall and radar data [3], soil moisture deficit data [4] [5], and for some probabilistic forecast methods [6] [7] [8] suggest that improvements in data collection, assimilation and modelling are needed, as are the human responses to flood warnings. Real time flood warning systems are not yet the norm in the
UK
. There is too much reliance on radar data which is either not detailed enough for small catchments or is simply inaccurate [3]. Following recent flooding the UK Government produced a review of flood resilience [9]. This tended to focus on the provision of rainfall simulations for probabilistic forecasting, the effects of climate change, but missed out small scale effects such as neglected drainage ditches and road levels becoming higher than household thresholds over a long period of successive road resurfacing. While there has been a call to replace the 1 in 100 year style of describing a flood [10] since it is said to be “confusing” to the public, the general level of understanding of flood frequency and especially flash flooding is so low that a much more practical approach is needed. This is especially true for surface water flooding which in the main, is caused by changes in surface hydraulic properties and inadequate road drainage, especially raised road levels. For example, in the Upper Brue at Bruton the main road has been raised by 0.5 m in the past 150 years, and at Combe in Oxfordshire the road had been raised about 0.3 m which led to floodwaters entering nearby houses. While flash floods caused by surface water is unlikely to cause death from drowning a much more serious risk is from river flooding in small rural catchments. The Land Drainage Act [11] states that where a flood warning system can be produced and is requested, the authorities have a duty to act accordingly. However, the level of understanding following the Boscastle flood of 2004 in
Cornwall
UK
can be summed up:
“It’s not possible to accurately forecast flooding in some areas such as parts of north Cornwall, where steep valleys mean that rivers can rise so rapidly after heavy rain that, with current technology, there’s not enough time to issue warnings” [12].
However, a real time warning system had already been provided for the upper Brue [13] and which was tested against the smaller Valency river at Boscastle where the catchment area is 20 km2, to give 1 hour warning on
16th August 2004
[14]. The non-linear flow model has now been extended over the whole of
England
and
Wales
[15] for design flood estimation, and with suitable soil hydraulic conductivity data it can be tested against actual storm events such as the most severe flood that has ever taken place in recent history, namely the Lynmouth flood on the East and
West Lyn
. whose catchment areas are 77 km2 and 22 km2 respectively. To date, this is the most severe test of the method. While Ciervo et al. [16] have used post event surveys to simulate a flash flood the present example is the first which uses both real time rainfall measurements and soil data gathered in the field. In addition where there is a significant soil moisture deficit at the start of the storm the model uses field based measurements of SMD which have been found to be much more reliable than calculated values [5]. It is contended that only with locally based field measurements can reliable flood warnings for fast reacting catchments be made both in the
UK
and elsewhere. This approach is in contrast to WMO [17] which states: “The difficulty of in situ monitoring of catchment wetness by conductivity or lysimeter measurements makes the use of these techniques very uncommon in flood forecasting operations”.
The remainder of this paper will give a description of the evolution of the flow model, how it has been tested in over 600 catchments in
England
and
Wales
, and how the measurement of in situ SMD has been carried out using low cost weighing lysimeters. Unlike some flow models which are computationally demanding, the current model can be used on an ordinary PC. With the SMD data posted daily on a website it can be accessed and input to the model. The model can also be used to produce flood frequency estimates. These are made more robust when field surveys of bankfull discharge are made, which in many rivers worldwide has a frequency of about 1.1 - 2.0 years. While the biggest catchment that the model has been tested is around 650 km2 it is on small flashy catchments that its value for providing timely warnings may be appreciated.
2. The Nonlinear UH Flow Model
The Unit hydrograph (UH) method has a long history being based on the work of
Sherman
[18]. Young and Bevan [19] have used a non-linear response since it is widely recognised that many hydrological processes are non-linear. The need to model non-linear responses in hydrology has also been promoted by Sivakumar [20]. The unit hydrograph method needs the following data and analysis in order to produce an estimate of the flood before the flood arrives:
1) Real time measurement of storm rainfall intensities
2) The antecedent soil moisture deficit (SMD) based on weighing lysimeter observations
3) An estimate of slope runoff when the SMD is zero
4) The percentage runoff at each stage of the storm event based on measured soil hydraulic conductivity
5) Conversion of the runoff depth into quickflow discharge
6) Conversion of the remaining rainfall into delayed flow discharge
7) Summation of quickflow and delayed flow to give total discharge
The first version of the flow model was developed as a flood warning tool for the Environment Agency to be used for flood warning at Bruton in
East Somerset
which is situated below a flood detention dam [13]. The approach to calibration of the model is data based mechanistic in that the autographic rainfall and estimates of peak discharge and timing of the flood events of 1968, 1974, 1979, and 1982 were used to produce the algorithms. The non-linear behaviour of the upper Brue catchment with an area of 31 km2 suggested that the change in discharge rate was of a logistic borrowed from biology which mimics autocatalytic monomolecular reactions Street & Opik, [21]:
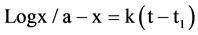 (1)
(1)
where t and t1 are time intervals, k = constant, a = maximum size, x = a given value.
This equation can be rewritten and optimised for the Brue dam site for the rising stage of the hydrograph:
Y = [INVLOG2(t − 0.7Tp)/1 + INVLOG2(t − 0.7Tp)]Qp (2)
where Tp = time to peak, t = time since start of storm, Qp = peak runoff rate per mm net rainfall and is related to Tp as follows:
Qp = (330/Tp) A/1000 (3)
where A = catchment area (km2).
For the falling limb:
Y = [INVLOG(t1 − 0.85(TB − Tp))/1 + INVLOG(t1 − 0.85(TB − Tp))]Qp (4)
where TB = time base and is related to Tp as follows:
TB = 2.52 Tp (5)
The time interval t1 is then related to TB as follows:
t1 = TB − t (6)
The delayed flow was calculated using a maximum value of 0.3896 m3・s−1・mm−1. There is a time lag of 2 hours before delayed flow starts and a further 2 hour delay for peak delayed flow to occur. Thereafter a linear decay function was used. The model was calibrated using the storm events of 1968, 1974, 1979, and 1982. For these events the time to peak decreased with increasing rainfall intensity (13), and by implication storm rarity, an observation that has been noted elsewhere [22]. The relationship between maximum rainfall intensity (R) and time to peak (Tp):
Tp = (2.4073R + 10.1005)/R (7)
There are no measured flow records for the upper Brue but autographic measurements of rainfall have been made at
North Brewham
since 1966. As a further check, the estimated rainfall hyetograph of the 1917 storm [23] was also used. The results are shown in Table 1.
These were based on field observations of the timing of over-bank and peak discharge and estimates of the peak discharge based on hydraulic calculations [24].
The result for the 1917 storm gave a peak discharge similar to that estimated from wrack marks and hydraulic calculations.
The flow model was adopted by the Environment Agency during 2004 and has
![]()
Table 1. Comparison of estimated peak discharge (cumecs) in the field and using the runoff model.
been in use for over 10 years. On
1 December 2005
it was able to predict the water level behind the flood detention dam upstream of Bruton to within 0.1 m. This result is considered to be accurate enough to issue a flood warning with a lead time of about 2 hours if the predicted water level is expected to get within 0.2 m of the level at which flow down the spillway takes place.
3. Calibration and Application to Ungauged Catchments
There are many hydrological models which can be calibrated for one catchment. It is quite another to produce a method that can be applied when there is no riverflow data and even more demanding to provide a sensible flood warning. Hydrological reasoning suggested that the time to peak, Tp, not only depends on the rainfall intensity but also on the permeability of the soil. Thus the equation for the upper Brue was generalised:
Tp = c(R−0.17) MSL catch/MSL Brue (8)
MSL = mainstream channel length (km) for the study catchment and Brue.
c = 7[INVLOG(0.06633(50 − %R))]/1 + INVLOG(0.06633 (50 − %R))] (9)
where %R = % runoff at rainfall equal to 10 mm・hr−1, the %R being based on the Ksat survey data for values 1% - 50%. For %R > 50% at rainfall 10 mm・hr−1, the equation for c becomes:
c= 3.5 (0.98 exp (%R − 50)) (10)
Adjustments for catchment slope and the mainstream catchment slope were also made. These changes were based on the Dudwell at Burwash, Ancholme at Toft Newton, and Brue at Bruton calibration catchments. The catchment and mainstream slope have correction factors. For catchment slope the correction factor (Scf) which best fit the data from 8 calibration catchments:
Scf = 1.7 [INVLOG(0.35(S − 3.30))/1 + INVLOG(0.35(S − 3.30)] (11)
where S = average catchment slope in degrees. This was assessed by counting the number of 10m changes in elevation on 1:50000 OS maps in each grid square or part grid square over a distance of 1km. The results are summed and then applied:
Tanslope = 0.01[Sx/A] (12)
where Sx = sum of changes in land height, A = catchment area.
The lowest value of Scf is 0.292 as found for the Ancholme at Toft Newton. Its general form is that of a logistic in that there is a minimum and maximum value which is attained at an ever decreasing rate at both low and high slopes. The constant 3.30 is the average slope for both the Brue and Lud catchments. The constant 0.35 influences the rate at which the value of Scf changes with slope.
The correction for mainstream channel slope is based on the gradient of the last 10 m fall in the mainstream (m/km). Where the gradient is lower further upstream up to a point which includes 50% or more of total catchment area, this gradient should be used. Again, considerable experiment yielded the correction factor for mainstream slope (MSScf):
MSScf = (2/L)F − (L1.001 − L) (13)
where L = distance between two 10 m contours on 1:50,000 OS maps, measured along the mainstream channel closest to the outlet.
F 0.7[(INVLOG(Log220 − LogA)/1 + INVLOG(Log220 − LogA) (14)
with a minimum value of 0.3. Where the point of interest is close enough to a confluence so that both tributaries are included in the 10 m height drop, the area weighted value of L is used. If L = or < 2.0 km then MSScf = 1.0.
Further adjustments for the lag time and time to peak of the delayed flow were made:
Lag/Tp = MSL catchment/MSL Brue (15)
where MSL = mainstream channel length as shown on 1:50,000 OS maps. Delayed flow increases linearly upwards until it reaches the peak. Thereafter it decreases exponentially according to the decay constant k, (Equation (24)), which varies with catchment area (A) via:
k = 0.0247LogA + 0.909 (16)
This is applied to the delayed flow via:
DelT + 1 =DelT exp k (17)
For the estimation of SMD a weighing lysimeter is used in the upper Brue catchment. The design of this has already been described [4] and a comparison of the results with both MORECS [5] and MOSES [25] have been given. Big differences between the measured and calculated values makes its effect on provision of a flood warning considerable.
4. Flood Warning for the Lynmouth Storm August 16 1952 Using the Flow Model
This flood resulted from over 9 inches (229 mm) taking place in about 9 hours on a catchment which was already at field capacity. The effects of the resulting flood have been described by Delderfield [26], Prosser [27]. Figure 1 shows the daily rainfall which has recently been revised according to an analysis of the effect of elevation on rainfall depth during the storm.
There were no rainfall recorders in the local area but 22 km to the west at Chivenor and 15 km to the east at Wootton Courtenay the combined continuous records enabled an estimated rainfall profile to be constructed. Figure 2 shows the results.
The percentage runoff at different rainfall intensities was estimated by measuring the saturated hydraulic conductivity of the soils in the field using the core method [28] Arellano & Clark, [29]. For each soil Association in the catchment at least 30 tests were made. The results were classified into 5 mm bands viz 0 - 5, 5.1 - 10 and so on as shown in Table 2.
![]()
Figure 1. Daily rainfall for 16 August 1952.
![]()
Figure 2. Estimated rainfall profiles for the East and West Lyn catchments.
Percentage runoff calculated from the midpoint in each class of conductivity: Eg. 20 mm・hr−1 percentage runoff = (20 − 2.5) ´ 0.31) ´ (20 − 7.5) ´ 0.23 + (20 − 12.5) ´ 0.20 + (20 − 17.5) ´ 0.11 = 50%. The percentage cover of each Soil Association was then measured from the Reconnaissance Map [30], and the catchment average % runoff calculated based on this and the conductivity values of each soil. Figure 3 shows the results.
The flow model is non-linear because of the response of soils to increasing rainfall intensity and the UH ordinates or rates of runoff per mm net rainfall being non linear with time.
Variables of the unit hydrograph method:
Time to peak (hours) = c MSL catchment/ MSL Brue (9) (R−0.17), where R = rainfall intensity mm・hr−1.
MSL = mainstream channel length (longest tributary) East Lyn = 17.27 km.
c = 7[INVLOG 0.06633 (50 − %R)/1 + INVLOG (50 − %R)].
![]()
Table 2. Saturated hydraulic conductivity of the Lydcott Association (654b).
![]()
Figure 3. Saturated hydraulic conductivity of soils in the East and West Lyn.
%R = percentage runoff at 10 mm・hr−1 rainfall, based on soil hydraulic conductivity.
For the
East Lyn
%R = 36. Thus c = 6.2619.
Time to peak = 12.015 (R−0.17).
Time base (TB) = 2.52Tp.
Peak quickflow ordinate (Qp) = 330/Tp x catchment area/1000.
Ordinates (Y) of the rising limb of the hydrograph:
Y = [INVLOG2(t − 0.7Tp]/1 + [INVLOG2(t − 0.7Tp)]Qp.
For the falling limb: Y = [INVLOG(t1 − 0.85(TB − Tp))/1 + INVLOG(t1 − 0.85(TB − Tp))]Qp. Where t1 = TB − T where T = time since start of storm.
The model is unique in that Tp, TB, and Qp will change at each stage of the storm according to the rainfall intensity. Slope runoff = R [sine average catchment slope (degrees)] = R [0.01 (N/A)] where N = sum of contour crossings in each grid square or part thereof on a 1:50,000 OS map over a straight or curved distance of 1km. A = catchment area. For East Lyn sine slope = 0.142.
Slope correction factor (Scf) = 1.7 [INVLOG(0.35(S − 3.30))/1 + INVLOG(0.35(S − 3.30))] where S = average catchment slope (degrees). For the East Lyn Scf = 1.667
Mainstream channel slope correction factor = 1.0 since distance between river channel contours < 2.0 km.
Hourly storm intensity, East Lyn : 2, 2, 15, 12, 8, 25, 20, 10, 30, 35, 6, 2
Extract of results:
where SR = slope runoff; K = runoff from the soil (hydraulic conductivity) T = SR + K. Del = Rainfall − T.
Extract from the unit hydrograph calculations is shown below. Body of the Table are ordinates (m3・s−1・mm−1 runoff. T = total runoff for each rainfall intensity. Total discharge is sum of the products at each time: eg. at 7 pm = 0.41 ´ 0.240 + 0.41 ´ 0.002 + 7.42 ´ 0.655 + 5.51 ´ 0.003 = 4.97. The discharges are cumecs (m3・s−1). The ordinates for delayed flow are 0.15 m3・s−1 31 km−2 which is for rock Group D2 and D1 [14]. The time to peak and lag time of delayed flow = MSL catch/MSL Brue. Linear increase in the ordinates up to peak and exponential decay rate thereafter viz: decay constant = 0.0247LogA + 0.909.
Total discharge = Scf ´ quickflow + delayed flow: (1.667 ´ 214) + 23.5 = 380 m3・s−1. Baseflow is added via Q = CA (INVLOG[0.0005372 SAAR − 2.3114]) = 3 cumecs therefore Q = 383 m3・s−1.
Figure 4 shows the complete hydrographs for the East and West Lyn . The main events of the flood have been simulated. This gives a measure of the robustness of the method in view of the extreme nature of the storm with more than one rainfall peak. The falling limb should have been about 30 minutes earlier. This would have allowed PC Derek Harper to get across the parapet of Countisbury Bridge by 0400 h [27]. The peak discharges of 384 and 162 cumecs for the East and West Lyn respectively are 8% and 36% lower than the results of Dobbie and Wolf [31].
Taking the West Lyn first the heavy rainfall up to 1800 hrs gives no cause for concern. By 1900 hrs considerable overflow in Lynmouth is predicted since the discharge has become about double the channel capacity. People warned might simply move upstairs perhaps taking special belongings. By 2000 h the situation would look not much worse but by 2030 h there was a clear sign that people should evacuate at once. Recall now the events 2 km upstream at Barbrook [26]. At some time after 2130 h Tom Floyd looked out to see the raging river, but by then it was too late. Fortunately Tom, his daughter, and dog Tim survived, but
![]()
Figure 4. Predicted hydrographs for the East and West Lyn. The time of each forecast is shown.
the rest of his family were drowned [27]. We can now say that at least 1 hour’s warning could have been given to the people at Barbrook, where four of the cottages were destroyed. On the East Lyn the longer travel distance gave more time to evacuate since by 1800 h the prediction of a life threatening flood is clear (Figure 4). Comparing the timing of this knowledge with events on the ground gives us hope for the future provision of flood warnings in the UK . At Bevan’s Cottages on the East Lyn the doors burst open at about 2150 h. Thus over three hours warning could have been given. Such is the sad loss of life for want of a timely flood warning!
5. Flood Warning for Boscastle
This event is included in this paper because the flow model was able to predict the flood with just over one hour warning. What has been described as the miracle of Boscastle is the fact that no one was drowned. However, several people, including visitors in the Wellington Hotel, had an escaped with a matter of a few minutes to spare, while a child sat on the bonnet of a car was grabbed seconds before the car was swept away. That the event happened in the day may have meant fewer people were present as visitors but the situation could have been a lot worse like at Lynmouth where people were tending to have a quiet evening indoors.
The storm was caused by a complex area of low pressure to the west with unstable air developing during the morning [32]. During a four hour period over 180mm were recorded at Lesnewth which is close to the centre of the Valency catchment which discharges into the Atlantic Ocean at Boscastle. Figure 5 shows the storm rainfall at a resolution of 0.25 hr.
The flow model used locally gathered soil hydraulic conductivity data. Full details of the application are given in Clark [14]. The river Valency started to overflow by 1515 hr. Three simulations were made and that for 1415 hr showed that a substantial flood was about to begin: a serious flood warning would then have been issued. Figure 6 shows the results.
The success of the model in giving a realistic estimate of the complete flood is shown in Figure 7. Calculations of the likely SMD showed that it was about 12 mm [33]. In contrast to this the MOSES PDM [34] suggested a value in excess of 100 mm which was far too high based on the rainfall regime earlier in the year and that at CHRS the weighing lysimeter on the same day was about 30 mm
![]()
Figure 5. Storm rainfall at Lesnewth 16 August 2004.
![]()
Figure 6. Estimated hydrographs for 16 August. The time of each forecast is shown.
![]()
Figure 7. Estimates of the discharge for 16 August 2004 at Boscastle [35].
SMD but with a lower rainfall in the previous three months. The lysimeter is 235 mm diameter and the soil about 330 mm deep, and costs about £25 to construct.
6. Discussion
Timely flood warnings are essential during a serious flash flood if lives are to be saved. The method described here uses local data for rainfall and soil hydraulic conductivity. The use of a low cost lysimeter in order to get realistic estimates of SMD has been briefly mentioned. This approach is much more realistic than other methods which fail to produce timely warnings. In a country which already has some places protected up to about the 1 in 100 year design standard the need for flood warning is even more important in the event of the scheme being overwhelmed by a very rare flood. There are also other places without any protection or even a flood warning scheme. For catchments below about 15km2 the lead time for a warning becomes less than 1 hour. Giving a false warning will undermine the confidence of future warnings so it is essential that accurate rainfall and catchment data are used. It is very much hoped that the techniques described here can be adopted in other countries.