Finite Temperature Lanczos Method with the Stochastic State Selection and Its Application to Study of the Higgs Mode in the Antiferromagnet at Finite Temperature ()
1. Introduction
The recent discovery of the Higgs particle [1] in the particle physics [2] [3] has stimulated study of the Higgs mode in the condensed matter physics [4] .One can find many experimental reports on the existence of this mode [5] - [11] . Among them we note that the experiment of superconducting films [12] close to the quantum phase transition gives us the strong evidence for the Higgs mode. In addition, theoretical study based on the sigma model, the spin wave theory and other effective models has been active. The purpose of the study is to find experimental conditions to observe the Higgs mode clearly [13] - [22] . Another purpose is to understand the role of this mode near the critical point of the quantum phase transition [23] - [28] .
In a previous study [29] we have studied the Higgs mode in the spin-1/2 Heisenberg antiferromagnet on the square lattice at zero temperature. It is well known that many materials realize the Heisenberg antiferromagnet because of its quite simple Hamiltonian. This system has been studied extensively by several numerical methods [30] [31] [32] as well as by the spin wave theory [33] . One motivation of the previous study is to find directly the numerical evidence for the Higgs mode in the quantum antiferromagnet by the reliable method. Another motivation is to investigate how the Higgs mode is induced from the fundamental Hamiltonian. Since the Higgs mode is the resonance state and can couple with two Goldstone-Nambu modes, we have calculated the dynamical correlations of the two spin operators on the finite lattice using the exact diagonalization approach. On the finite lattice we cannot find the resonance itself, but we can find several excited states instead. Taking this into account we have proposed four procedures to find the evidences for the resonance. The results have showed that we can find the Higgs mode in the dynamical correlations of the two spin operators. Also we have clarified differences between the Higgs modes in the SU(2) symmetry and those in the U(1) symmetry through the study of the XXZ model [29] .
In order to confirm that the Higgs mode exists at finite temperature, we would like to study the Higgs mode in the spin-1/2 Heisenberg antiferromagnet on the square lattice using the finite temperature Lanczos method (FTLM) [34] - [39] . When we apply the FTLM to calculations of the dynamical correlations of the operators at finite temperature, we use the set of the states generated by the Lanczos method to calculate the matrix elements of the operator between these Lanczos states. In the calculation at zero temperature the matrix elements are calculated between the Lanczos states and the ground state. In these calculations we need to keep the ground state, but we do not need to keep the Lanczos states after we calculate the matrix elements. In the calculations at finite temperature, on the other hand, we generate two kinds of sets of the Lanczos states. We then calculate the matrix elements between the Lanczos states of one set and the Lanczos states of another set. For these calculations we have to keep two kinds of sets of the Lanczos states on computer memory. For this reason we need the more memory than that of the calculations at zero temperature, or that of the calculations of the specific heat at finite temperature [39] .
Here we propose a use of the stochastic state selection (SSS) method [40] for calculations of the matrix elements in order to weaken the limitation on the computer memory. This method has been proposed and developed by T. Munehisa and Y. Munehisa thirteen years ago [40] - [47] . For the spin-1/2 antiferromagnet, the number of the basis states amounts to 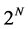 with the lattice size
with the lattice size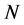 , i.e. we need
, i.e. we need 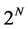 coefficients for one state. We select coefficients stochastically so that we force some to be zero and replace others by some finite values. The result from one sampling is not correct, but we can obtain the correct value after making the statistical average. Applying the SSS method we can drastically reduce the number of the basis states with non-zero coefficients. Then the limitation from the memory is relaxed. By this method it is possible to calculate the dynamical correlations on the
coefficients for one state. We select coefficients stochastically so that we force some to be zero and replace others by some finite values. The result from one sampling is not correct, but we can obtain the correct value after making the statistical average. Applying the SSS method we can drastically reduce the number of the basis states with non-zero coefficients. Then the limitation from the memory is relaxed. By this method it is possible to calculate the dynamical correlations on the 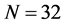 lattice using the moderate computer whose memory is 64 GB. Note that there is no other method so far to precisely calculate the matrix elements by small portions of the whole states.
lattice using the moderate computer whose memory is 64 GB. Note that there is no other method so far to precisely calculate the matrix elements by small portions of the whole states.
After numerical examinations of the SSS method in the FTLM, we present results about the Higgs mode at finite temperature. At low temperature we find the Higgs mode, whereas at high temperature we do not find this mode. We estimate two bounds of temperature by the strict and the loose conditions, under which we can find the Higgs mode. Our results on the lattices from 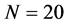 to
to 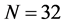 show that the Higgs mode exists at low temperature and it disappears gradually when the temperature becomes large from the lower bound to the higher bound.
show that the Higgs mode exists at low temperature and it disappears gradually when the temperature becomes large from the lower bound to the higher bound.
Contents of this paper are as follows. In the next section we present a brief description of calculations in the FTLM which will show the reason why a large number of the Lanczos states are necessary. Sections 3 and 4 are devoted to the SSS method. After explaining the SSS method in Section 3, we present numerical examinations of the SSS method in the calculations of the dynamical correlations in Section 4. Then in Section 5 we calculate the dynamical correlations in the spin-1/2 Heisenberg antiferromagnet on the square lattice in order to find the resonance that is associated with the Higgs mode. The final section is for summary and discussion of this work.
2. Dynamical Correlations and FTLM
In this section we give a brief description of the dynamical correlation and of the FTLM we use in our calculations. The dynamical correlation of the operator  and
and  is defined by
is defined by
 (1)
(1)
Here  and
and 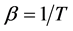 is the inverse of the temperature
is the inverse of the temperature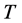 . Using the eigen value
. Using the eigen value 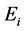 and the eigen state
and the eigen state 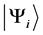 of the Hamiltonian
of the Hamiltonian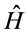 , we obtain
, we obtain
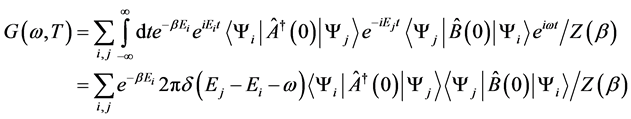 (2)
(2)
It is not possible to calculate every eigen value and every eigen state on the lattice whose size is more than 15 because the number of the matrix element is more than . Therefore we approximate the trace calculation using the random state
. Therefore we approximate the trace calculation using the random state  [48] [49] ,
[48] [49] ,
![]() (3)
(3)
We therefore calculate the following ![]() instead of
instead of![]() ,
,
![]() (4)
(4)
where
![]() (5)
(5)
When ![]() is infinitely large,
is infinitely large, ![]() agrees with
agrees with![]() .
.
In the FTLM, instead of the exact values and the exact states, we use the eigenvalues and the eigen states that are calculated by the set of the Lanczos states. A set of the Lanczos states ![]() is generated repeatedly,
is generated repeatedly,
![]() (6)
(6)
When M is of order of 100, it is easy to obtain the eigenvalues of![]() .
.
In the Lanczos method of the FLTM, it is important to choose an appropriate initial state for a good approximation. Therefore in calculations of
![]() given by (4), the first and second exponents of the Hamiltoniant are separately approximated by the suitable sets. As a result we need two sets of the Lanczos states, which are denoted by
given by (4), the first and second exponents of the Hamiltoniant are separately approximated by the suitable sets. As a result we need two sets of the Lanczos states, which are denoted by ![]() and
and![]() . The first state
. The first state ![]() of the set
of the set ![]() is given by
is given by
![]() (7)
(7)
where ![]() is a normalization factor,
is a normalization factor,
![]() (8)
(8)
Similarly the first state ![]() of the set
of the set ![]() is given by
is given by
![]() (9)
(9)
where ![]() is a normalization factor,
is a normalization factor,
![]() (10)
(10)
Let us denote the i-th eigen value of the Hamiltonian ![]() in the set
in the set ![]() by
by ![]() and the eigen state by
and the eigen state by![]() , while in the set
, while in the set ![]() they are denoted by
they are denoted by ![]() and by
and by![]() . The first exponential operator
. The first exponential operator ![]() is replaced by the set
is replaced by the set![]() ,
,
![]() (11)
(11)
Similarly the second exponential operator ![]() is replaced by the set
is replaced by the set ![]()
![]() (12)
(12)
When we use these eigenvalues and eigen states, we obtain the following expression for![]() ,
,
![]() (13)
(13)
We cannot calculate the ![]() -function on the finite lattice because of the discrete eigenvalues. Instead of this singular function, therefore, we use a regular function with a parameter
-function on the finite lattice because of the discrete eigenvalues. Instead of this singular function, therefore, we use a regular function with a parameter![]() ,
,
![]() (14)
(14)
Based on the discussions in [29] , we make ![]() a moderate value in order to examine peaks of
a moderate value in order to examine peaks of ![]() that are made by several eigen states. Then we obtain the following expression
that are made by several eigen states. Then we obtain the following expression
![]() (15)
(15)
3. Stochastic State Selection Method
In this section we briefly describe the stochastic state selection method [40] . A state ![]() is given by a set of a basis states
is given by a set of a basis states![]() ,
,
![]() (16)
(16)
Let us consider a probability variable ![]() for a parameter
for a parameter![]() , which is defined by
, which is defined by ![]() with the probability
with the probability ![]() and
and ![]() with the pro- bability
with the pro- bability![]() . The average of this variable is one, i.e.
. The average of this variable is one, i.e.
![]() Here
Here ![]() is the statistical average. Note that
is the statistical average. Note that![]() . We introduce a state
. We introduce a state ![]() to appro- ximate the state
to appro- ximate the state![]() ,
,
![]() (17)
(17)
where ![]() is a probability variable generated with
is a probability variable generated with![]() . Here
. Here ![]() is a parameter to control the accuracy of
is a parameter to control the accuracy of ![]() and the number of the selected states in the SSS method. When we make the statistical average of
and the number of the selected states in the SSS method. When we make the statistical average of![]() , we obtain the correct state,
, we obtain the correct state,
![]() (18)
(18)
The statistical average of number ![]() of basis states with non-zero coefficients in the sampling is given by
of basis states with non-zero coefficients in the sampling is given by
![]() (19)
(19)
Next we consider an inner product ![]() of two states
of two states ![]() and
and![]() . Using
. Using ![]() in (17) and
in (17) and
![]() (20)
(20)
where ![]() is a probability variable generated with
is a probability variable generated with![]() , we calculate the inner product,
, we calculate the inner product,
![]() (21)
(21)
If we make the statistical average of the inner product we obtain the correct value,
![]() (22)
(22)
In our calculation the statistical average ![]() is replaced by a sample average with a sample number
is replaced by a sample average with a sample number![]() ,
,
![]() (23)
(23)
where ![]() is a value of
is a value of ![]() in one sampling. When
in one sampling. When ![]() becomes infinitely lar- ge, the sample average agrees with the statistical average.
becomes infinitely lar- ge, the sample average agrees with the statistical average.
When ![]() becomes large the number of the non-zero
becomes large the number of the non-zero ![]() decreases, but the larger
decreases, but the larger ![]() is necessary for more accurate value. In order to estimate the required
is necessary for more accurate value. In order to estimate the required![]() , we calculate a variance
, we calculate a variance ![]() of the inner product, because the accuracy of the sample average is given by
of the inner product, because the accuracy of the sample average is given by![]() .
.
![]() (24)
(24)
For quantitative discussions let us assume that ![]() and
and
![]() for all i. Then we obtain
for all i. Then we obtain
![]() (25)
(25)
and
![]() (26)
(26)
If ![]() and
and![]() , we have
, we have ![]() and
and![]() . Thus we can obtain the inner product with satisfyingly small
. Thus we can obtain the inner product with satisfyingly small ![]() even if
even if
![]() . In this case we can obtain the accuracy of
. In this case we can obtain the accuracy of ![]() for the inner product
for the inner product![]() .
.
4. Numerical Examinations of SSS Method
In this section we present numerical examinations of the SSS method in the calculations of the dynamical correlations. Our model is the spin-1/2 Heisenberg antiferromagnet on the square lattice. The Hamiltonian is given by
![]() (27)
(27)
where ![]() is a spin operator on a site
is a spin operator on a site ![]() and
and ![]() denotes the nearest neighbor pair on the square lattice. The z-component
denotes the nearest neighbor pair on the square lattice. The z-component ![]() is a diagonal matrix, i.e. the basis state is defined by
is a diagonal matrix, i.e. the basis state is defined by ![]() where
where ![]() or
or![]() . Since our purpose is to investigate the Higgs mode, the operator
. Since our purpose is to investigate the Higgs mode, the operator ![]() and
and ![]() are the two spin operators. Namely
are the two spin operators. Namely
![]() [29] , where
[29] , where
![]() (28)
(28)
denoting the location of site i by![]() .
.
In the calculations of the dynamical correlations at finite temperature, we apply the SSS method to two sets of the Lanczos states, ![]() and
and![]() . In the calculations of
. In the calculations of![]() , we should keep
, we should keep ![]() coefficients on the lattice of the size N without the SSS method. When we apply the SSS method, on the other hand, we need to keep
coefficients on the lattice of the size N without the SSS method. When we apply the SSS method, on the other hand, we need to keep ![]() coeffici- ents instead. As we have discussed in section 3 we can impose
coeffici- ents instead. As we have discussed in section 3 we can impose ![]() which is much smaller than
which is much smaller than![]() .
.
Let us examine the accuracy by the SSS method then. For this examination we use a state ![]() instead of
instead of ![]() and calculate a correlation.
and calculate a correlation.
![]() (29)
(29)
instead of ![]() in (4). Following the procedure of having (15) from (4) in the section 2, we obtain
in (4). Following the procedure of having (15) from (4) in the section 2, we obtain
![]() (30)
(30)
where ![]() and
and ![]() are normalization factors,
are normalization factors,
![]() (31)
(31)
![]() (32)
(32)
Note that, from ![]() and
and![]() , we have
, we have
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
We apply the SSS method to ![]() and
and ![]() in order to obtain the SSS states
in order to obtain the SSS states ![]() and
and![]() . Using these states we define
. Using these states we define
![]()
(36)
Here ![]() denotes
denotes ![]() of the n-th
of the n-th
SSS sampling. When ![]() is infinitely large
is infinitely large ![]() agrees with
agrees with![]() .
.
As discussed in section 3, we have the parameter ![]() in the SSS method. When
in the SSS method. When ![]() is small the accuracy is high, but the number of the basis states to be kept is large. We would like to examine the accuracy and the cost in calculations of
is small the accuracy is high, but the number of the basis states to be kept is large. We would like to examine the accuracy and the cost in calculations of![]() . In Figure 1, we show our numerical results of
. In Figure 1, we show our numerical results of ![]() on the lattice
on the lattice ![]() with
with![]() ,
, ![]() and
and ![]() as a function of
as a function of![]() . In this figure we plot the difference
. In this figure we plot the difference
![]() given by
given by
![]() (37)
(37)
The error bar is the statistical error of![]() . Compared with the black data
. Compared with the black data![]() , the green data
, the green data![]() , are closer to zero. In comparison with the black data and the red data:
, are closer to zero. In comparison with the black data and the red data:
![]() , the latters are closer to zero. The average numbers of the basis states with non-zero coefficients in the SSS method are ~9500 with
, the latters are closer to zero. The average numbers of the basis states with non-zero coefficients in the SSS method are ~9500 with ![]() and ~37000 with
and ~37000 with![]() . In section 3 we have argued that the average number of the basis states with non-zero coefficients is drastically reduced to be of order of
. In section 3 we have argued that the average number of the basis states with non-zero coefficients is drastically reduced to be of order of ![]() by the SSS method. We see that the mea- sured values are a little less than
by the SSS method. We see that the mea- sured values are a little less than![]() , which are 12500 for
, which are 12500 for ![]() and 51200 for
and 51200 for![]() .
.
As for the accuracy of sample average, we have discussed that it would be proportional to![]() . Figure 1 shows that the error around
. Figure 1 shows that the error around ![]() is ~ 0.04 in the black data, ~ 0.01 in the red data and ~ 0.01 in the green data. Since {
is ~ 0.04 in the black data, ~ 0.01 in the red data and ~ 0.01 in the green data. Since {![]() (black data)}/{
(black data)}/{![]() (red data)} = 4 ~ 0.04/0.01 and {
(red data)} = 4 ~ 0.04/0.01 and {![]() (black data)}/{
(black data)}/{ ![]() (green data)} =
(green data)} =![]() , these results support the discussion in section 3.
, these results support the discussion in section 3.
![]()
Figure 1. The difference ![]() defined in (37) in the SSS method on the
defined in (37) in the SSS method on the
![]() lattice for the fixed state with
lattice for the fixed state with ![]() and
and![]() . They are plot- ted as a function of
. They are plot- ted as a function of![]() . Parameters
. Parameters ![]() and
and ![]() are 0.08 and 40 for the black data, 0.02 and 40 for the red data and 0.08 and 720 for the green data, respectively.
are 0.08 and 40 for the black data, 0.02 and 40 for the red data and 0.08 and 720 for the green data, respectively.
In order to examine ![]() using the SSS method, we define
using the SSS method, we define
![]() by
by
![]() (38)
(38)
![]() (39)
(39)
Note that here we set ![]() because one sampling for each random set will be enough when
because one sampling for each random set will be enough when ![]() is large. Further discussion on this point will be given in the final section.
is large. Further discussion on this point will be given in the final section.
Now we would like to examine the difference between ![]() and
and ![]() on the
on the ![]() lattice. Even on this small lattice, however, it is difficult to obtain
lattice. Even on this small lattice, however, it is difficult to obtain ![]() because we need all eigenvalues and eigen states for the correlations. We therefore use
because we need all eigenvalues and eigen states for the correlations. We therefore use ![]() here instead of
here instead of![]() . In Figure 2 we plot
. In Figure 2 we plot ![]() which is defined by
which is defined by
![]() (40)
(40)
where![]() , and
, and![]() . In order to examine the fluctuation of
. In order to examine the fluctuation of ![]() due to the sampling, we carry out calculations with four sets of
due to the sampling, we carry out calculations with four sets of ![]() for each
for each![]() . The observed four
. The observed four
![]() are plotted by the black circles
are plotted by the black circles ![]() and the red diamonds
and the red diamonds![]() . In Figure 2 we also plot results for
. In Figure 2 we also plot results for![]() , which are obtained without using the SSS method. Note that they should give us the minimum of the accuracy for
, which are obtained without using the SSS method. Note that they should give us the minimum of the accuracy for![]() . For both cases of
. For both cases of ![]() and
and![]() we observe that
we observe that ![]() and
and ![]() are almost the same order for any value of
are almost the same order for any value of ![]() we employed. This fact implies that in calculations of the dynamical correlations using the SSS method we do not need more number of the sampling compared to that without the SSS. By these examinations we conclude that we can apply the SSS method to calculations of the dynamical correlations.
we employed. This fact implies that in calculations of the dynamical correlations using the SSS method we do not need more number of the sampling compared to that without the SSS. By these examinations we conclude that we can apply the SSS method to calculations of the dynamical correlations.
5. Higgs Mode
The most important purpose of this paper is the numerical verification of the Higgs mode in the quantum spin systems at finite temperature. In this section we would like to show it by calculating the dynamical correlations in the spin- 1/2 Heisenberg antiferromagnet on the square lattice. Since the Higgs mode is the excited state and couples to the two Goldstone-Nambu modes, we have to calculate the dynamical correlations of the two operators that contain the Goldstone-Nambu modes. In the Heisenberg antiferromagnet the spin operators con- tain these modes. Therefore we calculate the following dynamical correlation, ![]() in (39) with the two spin operators
in (39) with the two spin operators
![]() .
.
In order to obtain stable results at any temperature, we employ the Chebyshev polynomial expansion [39] for the calculation of ![]() in (7) and (9),
in (7) and (9),
![]() (41)
(41)
with the k-th Chebyshev polynomial ![]() and the k-th coefficient
and the k-th coefficient![]() .
.
Before presenting our results we comment on parameters in our calculations, which we summarize in Table 1.
![]()
Table 1. Parameters of calculations; the symbol and the range in our calculations.
The inverse temperature ![]() and the energy
and the energy ![]() are the physical quantities.
are the physical quantities.
The lattice size ![]() is restricted because of the exact diagonalization approach.
is restricted because of the exact diagonalization approach.
In our work, we calculate on the lattices of the size![]() . For the periodic boundary condition we have two edge vectors
. For the periodic boundary condition we have two edge vectors ![]() and
and![]() . Since we impose the
. Since we impose the ![]() rotational symmetry to the Hamiltonian, the edge ve- ctor
rotational symmetry to the Hamiltonian, the edge ve- ctor ![]() is given by
is given by ![]() and the lattice size is given by
and the lattice size is given by![]() . Note that these edge vectors are defined uniquely for a given lattice size
. Note that these edge vectors are defined uniquely for a given lattice size ![]() except for an accidental case
except for an accidental case![]() . In this exceptional case we distinguish two different
. In this exceptional case we distinguish two different ![]() lattices by
lattices by![]() and
and![]() . For the lattices of
. For the lattices of
![]() and 32, the edge vector
and 32, the edge vector ![]() are (4, 2), (5, 0), (4, 3), (5, 1), (5, 2) and (4, 4), respectively.
are (4, 2), (5, 0), (4, 3), (5, 1), (5, 2) and (4, 4), respectively.
The wave vector ![]() is the non-zero wave vector of the lowest magnitude on the each lattice. For the lattices
is the non-zero wave vector of the lowest magnitude on the each lattice. For the lattices ![]() and 32, they are
and 32, they are
![]() and
and
![]() .
.
The parameters ![]() and
and ![]() control the accuracy of the Chebyshev polynomial expansion. They are determined by the request that the precision is of order
control the accuracy of the Chebyshev polynomial expansion. They are determined by the request that the precision is of order![]() . As a result they depend on values of
. As a result they depend on values of ![]() and
and![]() .
.
On the parameter ![]() in (14), we have presented the careful discussion in the previous work [29] . This discussion has showed that
in (14), we have presented the careful discussion in the previous work [29] . This discussion has showed that ![]() is most suitable. Therefore we use this value for
is most suitable. Therefore we use this value for![]() .
.
As for the number ![]() of the Lanczos states we fix it to be 50 following the discussion of the previous work [29] and the preliminary study. In the
of the Lanczos states we fix it to be 50 following the discussion of the previous work [29] and the preliminary study. In the ![]() lattice we use
lattice we use ![]() in order to reduce a huge calculation time.
in order to reduce a huge calculation time.
We apply the SSS method to calculations for![]() . The parameter
. The parameter ![]() is 0.01 for
is 0.01 for ![]() and 29, and is 0.04 for
and 29, and is 0.04 for![]() .
.
The sampling number of the random states ![]() is determined by requiring that the relative precision of our calculations on the dynamical correlations is 5%.
is determined by requiring that the relative precision of our calculations on the dynamical correlations is 5%.
In Figure 3 we present the dynamical correlations ![]() on the
on the ![]() lattice as a function of
lattice as a function of![]() . At the low temperatures
. At the low temperatures ![]() and 3.2 we find the broad peaks clearly, as expected. These broad peaks could be the Higgs mode which has been found at
and 3.2 we find the broad peaks clearly, as expected. These broad peaks could be the Higgs mode which has been found at ![]() in the previous work [29] . On the other hand, at the high temperature
in the previous work [29] . On the other hand, at the high temperature ![]() we cannot find any peak that is relevant with the Higgs mode. In order to confirm that we find the broad peak at the low
we cannot find any peak that is relevant with the Higgs mode. In order to confirm that we find the broad peak at the low ![]() in the contrast to no broad peak at high
in the contrast to no broad peak at high![]() , we plot the dynamical correlations at the low
, we plot the dynamical correlations at the low ![]() and those at the high
and those at the high ![]() on various lattices in Figure 4, where the correlations at
on various lattices in Figure 4, where the correlations at ![]() and those at
and those at ![]() are shown. The results in Figure 4 support our arguments.
are shown. The results in Figure 4 support our arguments.
What we are interested in is the shape of the dynamical correlation around the broad peak. Since the absolute value of the correlation strongly depends on![]() , we introduce a normalized correlation
, we introduce a normalized correlation
![]()
Figure 4. The dynamical correlations with ![]() and 1.2 for various lattices plotted as a function of
and 1.2 for various lattices plotted as a function of![]() . The error bars are the statistical errors.
. The error bars are the statistical errors.
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
in the range ![]() which covers the area of the broad peak at
which covers the area of the broad peak at![]() , so that we can easily compare our results for the different values of
, so that we can easily compare our results for the different values of![]() . We employ
. We employ ![]() and
and![]() , using the central energy of the board peak
, using the central energy of the board peak ![]() and the width
and the width ![]() at
at ![]() [29] . In Figure 5 we plot
[29] . In Figure 5 we plot ![]() on the
on the ![]() lattice as a function of
lattice as a function of ![]() for various values of
for various values of ![]() between 1.12 and 10.0. We see that the broad peak gradually disappears as
between 1.12 and 10.0. We see that the broad peak gradually disappears as ![]() becomes small. For example we can clearly find the broad peak at
becomes small. For example we can clearly find the broad peak at![]() , while it is not easy to find the peak when
, while it is not easy to find the peak when ![]() and there is no peak at
and there is no peak at![]() .
.
We would like to determine a boundary of ![]() below which the broad peak vanishes. It is, however, difficult to estimate such boundary temperature because the broad peak disappears gradually when
below which the broad peak vanishes. It is, however, difficult to estimate such boundary temperature because the broad peak disappears gradually when ![]() decreases. Therefore we introduce two kinds of
decreases. Therefore we introduce two kinds of![]() , which we denote
, which we denote ![]() and
and![]() . We can insist that the broad peak exists for
. We can insist that the broad peak exists for![]() . On the other hand we admit that it is difficult to find the broad peak for
. On the other hand we admit that it is difficult to find the broad peak for![]() . In other words
. In other words ![]() is a boundary by the strict condition for the broad peak, while
is a boundary by the strict condition for the broad peak, while ![]() is a boundary by the loose condition for it. On the
is a boundary by the loose condition for it. On the ![]() lattice we estimate that
lattice we estimate that ![]() and
and![]() .
.
On other lattices we can determine ![]() and
and ![]() in the same way. When the lattice size
in the same way. When the lattice size ![]() is odd we observe that
is odd we observe that ![]() and
and ![]() scarcely depend on
scarcely depend on![]() . In Figure 6 we show the normalized correlations
. In Figure 6 we show the normalized correlations ![]() for
for ![]() and those for
and those for ![]() on the
on the ![]() and 29 lattices. On the even-size lattices of
and 29 lattices. On the even-size lattices of ![]() and 32, on the contrary, the shapes differ from each other. As a result we cannot determine a common value for
and 32, on the contrary, the shapes differ from each other. As a result we cannot determine a common value for ![]() or
or![]() . Our estimations are
. Our estimations are ![]() for the
for the ![]() lattice,
lattice, ![]()
![]() for the
for the ![]() lattice and
lattice and ![]() for the
for the ![]() lattice. In Figure 7 we plot the normalized correlations for
lattice. In Figure 7 we plot the normalized correlations for ![]() and those for
and those for ![]() on the
on the ![]() and 32 lattices.
and 32 lattices.
Such difference between the results on the odd-size lattices and those on the even-size lattices is ascribable to the behavior of the correlations at ![]() [29] . As shown in Figure 6 and Figure 7, values of
[29] . As shown in Figure 6 and Figure 7, values of ![]() fluctuate more on the even-
fluctuate more on the even-
![]()
Figure 5. The normalized dynamical correlations for various values of T on the ![]() lattice. The vertical red dotted line shows the value of
lattice. The vertical red dotted line shows the value of![]() .
.
size lattices than those on the odd-size lattices. Especially we observe that
![]() . As for the height of the broad peak, it becomes large when the width
. As for the height of the broad peak, it becomes large when the width ![]() is small because the normalization factor
is small because the normalization factor ![]() in (42) is calculated in the range between
in (42) is calculated in the range between ![]() and
and![]() . Values of the width we calculated are
. Values of the width we calculated are![]() , and
, and![]() , while
, while![]() , and
, and![]() .
.
The behavior of the dynamical correlations on the ![]() lattice is much different from those on larger lattices. It seems to be that the finite size effect is quite severe for this lattice size. Except for the
lattice is much different from those on larger lattices. It seems to be that the finite size effect is quite severe for this lattice size. Except for the ![]() case we see the position of the broad peak shifts to lower
case we see the position of the broad peak shifts to lower ![]() when
when![]() , for which the Higgs mode with the total spin
, for which the Higgs mode with the total spin ![]() should contribute in addition to the mode with
should contribute in addition to the mode with![]() .
.
6. Summary and Discussion
In this research we have calculated, in order to find the Higgs mode, the dynamical correlations of the two spin operators in the spin-1/2 Heisenberg antiferromagnet on the square lattice at finite temperature. We have proposed an improved finite temperature Lanczos method using the stochastic state selection method for calculations on the lattices of up to 32 sites.
In the standard finite temperature Lanczos method we generate Lanczos states, calculate the eigenvalues and calculate matrix elements that are the values of the operator between two Lanczos states. In calculations of the matrix elements we have to keep the set of Lanczos states on the computer memory. Therefore the memory limits the system size for which we can calculate the matrix elements. Here we have proposed the application of the stochastic state selection method in order to weaken this limitation. This method is to select some parts of basis states stochastically and to abandon other basis states. Only by the selected basis states we calculate the inner product. After we make the statistical average, we can obtain the correct value of the inner product. By the stochastic state selection method we can drastically reduce the number of the basis states for the calculations.
In order to study the Higgs mode at finite temperature, we have calculated the dynamical correlations of the two spin operators in the spin-1/2 Heisenberg antiferromagnet on the square lattice, using the improved finite temperature Lanczos method. In calculations on the ![]() lattices we have found the broad peaks at low
lattices we have found the broad peaks at low![]() , while there have been no peaks relevant with the Higgs mode at high
, while there have been no peaks relevant with the Higgs mode at high![]() . Also we have found that the broad peak disappears gradually in the range
. Also we have found that the broad peak disappears gradually in the range ![]() on the odd-size lattices, and it disappears gradually in the range
on the odd-size lattices, and it disappears gradually in the range ![]() on the even-size lattices.
on the even-size lattices.
A few comments are in order. The first comment is about the parameter ![]() of the Lanczos state number. In the present calculations we used the value of
of the Lanczos state number. In the present calculations we used the value of![]() . At quite high temperature we need the larger value of
. At quite high temperature we need the larger value of![]() , because many states contribute to the correlations. In a case of
, because many states contribute to the correlations. In a case of ![]() and
and![]() , for an example, we find that the curve of the dynamical correlations vibrates when
, for an example, we find that the curve of the dynamical correlations vibrates when ![]() whereas we find the smooth curve when
whereas we find the smooth curve when![]() . We conclude that the vibration is unphysical and originates from the smallness of
. We conclude that the vibration is unphysical and originates from the smallness of![]() .
.
The second comment is about![]() , i.e. about the number of the sampling on the probability variables in the SSS method. In our calculations we have two kinds of the sampling, that are the sampling on the random state and the sampling on the SSS variables. In calculations of
, i.e. about the number of the sampling on the probability variables in the SSS method. In our calculations we have two kinds of the sampling, that are the sampling on the random state and the sampling on the SSS variables. In calculations of ![]() in (39), we set
in (39), we set![]() . It is possible to obtain the correct values of
. It is possible to obtain the correct values of ![]() when we make the sampling on the random state by large
when we make the sampling on the random state by large ![]() after making the sampling on the probability variables
after making the sampling on the probability variables ![]() by large
by large ![]() for each random state. But it is also possible to make the sampling on the probability variables
for each random state. But it is also possible to make the sampling on the probability variables ![]() and the sampling on the random state at the same time. This sampling means that we make one sampling on the probability variables of
and the sampling on the random state at the same time. This sampling means that we make one sampling on the probability variables of![]() , i.e.
, i.e.![]() , for each random state
, for each random state![]() . Adopting this sampling method, we can obtain the correct values of
. Adopting this sampling method, we can obtain the correct values of ![]() if we make the sampling by large
if we make the sampling by large![]() . The discussion on
. The discussion on ![]() was made in the study of the SSS method [43] extensively.
was made in the study of the SSS method [43] extensively.
The following three comments are about subjects for future study to be pursued. Since we employ the exact diagonalization approaches, the lattice size is severely limited even in the improved FTLM. Therefore it is desirable to make further study by other calculation methods, the high temperature expansions for example, which do not depend on the lattice size.
The results of this work and the previous work [29] suggest that one can find the Higgs mode in experiments of the quantum antiferromagnet on the square lattice if we measure the dynamical correlations of the two spin operators.
Another subject is about universality of the Higgs mode in the quantum spin systems. On the universality study the system on the triangle lattice is quite interesting because this system has the three kinds of the Nambu-Goldstone modes, whereas the system on the square lattice has the two kinds. It means that there must be an essential difference between both systems. Therefore it is very important to ask about what is the difference between the Higgs modes in these systems.
Acknowledgements
T. M. would like to thank Dr. Yasuko Munehisa for critical reading of the manuscript and for useful discussions.