Estimation of the Sensible and Latent Heat Fluxes by Reciprocal Analysis at an Arid and Semi-Arid Region ()
1. Introduction
Recently, we firstly reported reciprocal analysis of sensible and latent heat fluxes in a forest and humid region [1] [2] . By applying the procedure, this research highlighted the same problems in “an arid and semi-arid regions”. As is well known, the region usually faced to very severe water shortage. Therefore, reasonable estimation of latent heat flux (evapotranspiration) is very important issues. But the analysis in the local area still has a big problem because the flux severely affects local climate conditions.
Our proposed method is reciprocal analysis of the sensible and latent heat fluxes using single height temperature (Tz) and humidity (rehz) with net radiation (Rn) and heat flux into the ground (G). This method can’t be found out in the previous research except ours [1] [2] . This method is remarkably effective to extend the utilization for various regional areas.
One of the problems in the method is how to determine the initial values and constraints. This paper describes mainly focusing on this problems including estimation of those fluxes in arid and semi-arid region.
The results compare general solution (1) (solved two simultaneous equations that mathematically unified soil surface temperature (Ts) and humidity (rehs)), general solution (2) (solved one equation using Ts observed by radiometer that unified rehs mathematically) and conventional solution (solved one equation that not unified Ts and rehs mathematically). Furthermore, this research describes relationship between annual evapotranspiration and precipitation from the aspect of water balance.
Actually, the unknown variables in the proposed method, Ts and rehs, were estimated by the non-linear optimization technique known as the General Reduced Gradient (GRG) using the Excel Solver (Appendix 1) [1] [2] .
2. Methods
2.1. Method of Analysis
2.1.1. Fundamental Concept of the Model
The fundamental concept of the method is quiet similar with previous research. Here, we describe the outline briefly. The proposed model considers the near-soil surface as shown in Figure 1. Net radiation moves from air to the soil surface, and it is portioned into sensible, latent and underground heat fluxes. Ts is the soil surface temperature, Tz is the air temperature at height z, q(Tz) is the specific moisture at height z, rehz is relative
humidity in air at height z, q(Ts) is the unsaturated specific moisture on the soil
![]()
Figure 1. Schematic presentation of considered domain and used symbols [2] . (Symbols used in research defined as this figure. The net radiation Rn partitioned into ground G, sensible heat H and latent heat lE. Thus, Heat balance relationship Rn = H + lE + G is always guaranteed).
surface, and qsat(Ts) is the saturated specific moisture on the soil surface [1] [2] .
The fundamental formulae of the model satisfy the following well-known heat balance relationship [3] .
Heat balance relationship:
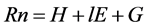 (1)
(1)
Here, Rn is the net radiation flux (W・m−2), G is the heat flux into the ground (W・m−2), H is the sensible heat flux (W・m−2), and lE is the latent heat flux (W・m−2).
In addition, the Bowen ratio (H/lE) is defined as follows [1] [2] [3] :
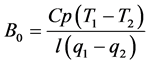 (2)
(2)
We apply the concept to the layer between the soil surface and observation height of Tz and rehz. However, the Ts and q(Ts) just on the surface are usually unknown.
2.1.2. Equation for Determining the Unknown Variables Ts and rehs
The purpose of the optimization is to determine the unknown variables Ts and q(Ts) without measurements. Initially, Ts and q(Ts), i.e., rehs ´ qsat(Ts), are assumed. Then it’s gradually improved according to the following optimization procedure [1] [2] :
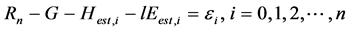 (3)
(3)
 (4)
(4)
 and
and 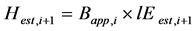 (5)
(5)
Here, i is number of iterations. Hest,i is estimated sensible heat flux in i times iteration, lEest,i is estimated latent heat flux of i times iteration, εi is residual of heat balance relationship of i times iteration, Tsass is assumed soil surface temperature, q(Tsass) is assumed specific moisture at Tsass, Bapp is apparent ratio of sensible and latent heat flux under convergence process
Repeating the above calculation, the Bapp goes to B0 according to the objective function where ABS (εi) reaches a minimum. Symbols used here presented in Figure 1.
Using the determined Bowen ratio (B0) after optimization, lE and H can be obtained as follows:
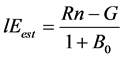 and
and  (6)
(6)
Symbols used here presented in Figure 1.
To estimate Ts, an adjustment factor RTs was introduced using T0 as follows:
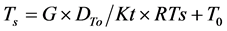 (7)
(7)
Here, T0 is the observed soil temperature at a depth of x cm, DTo is the depth of the soil temperature observation, Kt is the assumed temperature conductivity (W・cm−1・˚C), Equation (7) describes how to estimate Ts by extrapolating T0 using G, DTo and Kt [1] [2] .
2.1.3. Correction of the Heat Imbalance by Multiple Regression Analysis
The observed data have a heat imbalance that is well known as a “closure issue”. Twine, et al. [4] indicated an approximately 10% - 30% imbalance in H and lE. Wilson, et al. [5] also indicated that approximately 20% of the imbalance is due to heat flux. Allen [6] suggested that the under-measurement of lE is sometimes approximately 40%.
Table 1 describes the imbalance in the heat energy. Therefore, the data should be correct. According to Allen’s procedure, we corrected the data by multiple regression analysis using the observed data as follows [1] [2] :
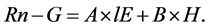 (8)
(8)
Here, Rn is the net radiation, G is the heat flux into the ground, lE is the latent heat flux observed, and H is the sensible heat flux observed. A is the regression coefficient for lE, and B is the regression coefficient for H. The corrected data are expressed as Hcor for H and lEcor for lE. The observed data are expressed as Hobs and lEobs, and the imbalance data are also defined as Himb ( ) for H and lEimb (
) for H and lEimb (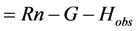 ) for lE.
) for lE.
2.1.4. Method of General Solution (1)
To uniquely estimate the unknown variables Ts and rehs, pair of two equations is required mathematically. We set the two equations as follows [1] [2] :
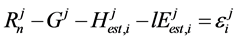 (9)
(9)
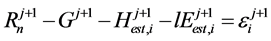 (10)
(10)
 goes to minimum. (11)
goes to minimum. (11)
Here, j is the order of hours from 1 to the end of the analyzed hours and i is the number of iterations.
The calculation is performed by solving Equation (9) and Equation (10) simultaneously under 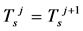 and
and  conditions.
conditions.
In addition, to prevent abnormal fluctuation of Hest and lEest in the optimization process, constraints![]() , lE are applied. The reason described in previous research [1] [2] . The constraints for Equation (9) and Equation (10) are follows:
, lE are applied. The reason described in previous research [1] [2] . The constraints for Equation (9) and Equation (10) are follows:
![]() (12)
(12)
Equation (9) and Equation (10) are nonlinear two element simultaneous equation. The two unknown variables can be estimated for the limit to which ε is minimized, allowing H and lE to be estimated. Note that the other factors are obtained from observations or calculations independently using the aforementioned relationships.
2.1.5. Initial Values for Ts and rehs
Setting of the initial value of Ts and rehs are the most important. Figure 2 describes the concept of the initial values in the plane of vapor pressure and temperature [e(T)~T] relationship. The dotted line indicates a partial vapor pressure for a given relative humidity. The saturated vapor pressure calculated by Tetens Formula.
On the plane, we can select two point as a[(Tz, e(Tz)] and b[T0, e(Tz)] using observed data. If we assume rehs = rehz, c[T0, e(T0)] point can be determined, thus, the hatched triangle can be defined as the initial values. The ratio of lEest/Hest is similar to ![]() [refer Equation (2) or Equation (3) if e(T) converted to q(T)]. We consider the optimized value of b’[Ts, e(Tz)] and c’[Ts, e(Ts)] as triangle with dotted line on the figure. We searched the optimal value b’[Ts, e(Tz)] and c’[Ts, e(Ts)] at the vicinity of the initial value b[T0, e(Tz)] and c[T0, e(T0)]. Based on the above concept, we set the initial value of
[refer Equation (2) or Equation (3) if e(T) converted to q(T)]. We consider the optimized value of b’[Ts, e(Tz)] and c’[Ts, e(Ts)] as triangle with dotted line on the figure. We searched the optimal value b’[Ts, e(Tz)] and c’[Ts, e(Ts)] at the vicinity of the initial value b[T0, e(Tz)] and c[T0, e(T0)]. Based on the above concept, we set the initial value of ![]() and rehs = rehz.
and rehs = rehz.
To guarantee better reproducibility, we set the constraints as Equation (13) as indicating in Figure 2 [2] :
![]()
Figure 2. Schematic expression of initial value of ![]() on the T~e(T) plane (The saturated vapor pressure T~esat(T)-relationship obtained by Tetens Formula (a). The unsaturated (partial) vapor pressure T~e(T)-line calculated by multiplying relative humidity (reh). lEest/Hest is similar to the relationship Ts − Tz over [q(Ts) − q(Tz)] from Equation (c). Specific humidity q(T) is proportional to vapor pressure (T). Thus, the hatched triangle is similarity to lEest/Hest. The ratio lEest/Hest is set as the initial value of optimization. The dotted triangle is a schematic presentation of converged ratio of lEest/Hest. The initial triangle point c[T0, e(T0)] should be set as possible as the vicinity of the final triangle point c’[Ts, e(Ts)]. That is very important things).
on the T~e(T) plane (The saturated vapor pressure T~esat(T)-relationship obtained by Tetens Formula (a). The unsaturated (partial) vapor pressure T~e(T)-line calculated by multiplying relative humidity (reh). lEest/Hest is similar to the relationship Ts − Tz over [q(Ts) − q(Tz)] from Equation (c). Specific humidity q(T) is proportional to vapor pressure (T). Thus, the hatched triangle is similarity to lEest/Hest. The ratio lEest/Hest is set as the initial value of optimization. The dotted triangle is a schematic presentation of converged ratio of lEest/Hest. The initial triangle point c[T0, e(T0)] should be set as possible as the vicinity of the final triangle point c’[Ts, e(Ts)]. That is very important things).
![]() (13)
(13)
b is a constant passing through a straight line at T = 0˚C with gradient![]() . The b is experimental constant to compensate the weakness of sensitivity in the optimization process. The maximum of b is defined as follows:
. The b is experimental constant to compensate the weakness of sensitivity in the optimization process. The maximum of b is defined as follows:
![]() (14)
(14)
Using b and bmax, the constraint set as follows:
![]() (15)
(15)
2.1.6. Actual Process of the Analysis
The estimate of Hest and lEest is performed as follows: First, the value of Ts is chosen from observed values (T0) collected near the soil surface. The rehs value is set to be the same as the rehz observed value. Second, the Ts and rehs are optimized together to satisfy the heat balance relationship using Equation (9) and Equation (10).
The values of εi are initially very small, on the order of 10−15 (W・m−2). Therefore, the objective function is multiplied by 1015. To avoid abnormal fluctuations of Hest and lEest, constraints on those variables are set as less than ABS (Rn − G). The constraints for Bapp are set at ![]() by referring to the singularity of convergence process [1] [2] and actual data. And also applied the constraint as
by referring to the singularity of convergence process [1] [2] and actual data. And also applied the constraint as![]() . The reason for these constrains is described in the discussion section.
. The reason for these constrains is described in the discussion section.
The calculation follows a non-linear optimization procedure that employs a General Reduced Gradient (GRG) algorithm, which can be applied with the Excel Solver on a personal computer (Appendix 1 and Appendix 2) [1] [2] .
2.2. Investigation Site and Equipment
To examine the proposed method, eight sites were chosen throughout the world as listed in Table 1: three sites are in the USA and Australia and one site is in Europe and China. The data of all sites were prepared by FLUXNET (Beringer, et al. [7] : Sturt Plains (AU-Stp) Ozflux L2 Data; Billesbach, et al. [8] : Woodward (US-AR2) Data; Ceschia and Tallec [9] : Lamasquere (FR-Lam) Data; Eamus and Cleverly [10] : Ti Tree East (AU-TTE) Ozflux L2 Data; Beringer J. and L. Hutley [11] : Dry River (AU-Dry) Ozflux L2 Data; Scott [12] : Lucky Hills Shrubland (US-Whs) AmeriFlux L2 Data; Wharton [13] : Diablo (US-Dia) AmeriFlux L2 Data; Yanhong, et al. [14] : Qinghai Flux Research Site (CN-QHB) AsiaFlux Data).
Table 1 shows the name of the sites, country, state/province, location, elevation, vegetation, tower height, plant height and year of examined data. The tested year ware chosen as well as minimize the data gaps.
Table 2 describes the type of instruments applied with the variables of the heat balance components, unit and description of those measurements, including temperature T0 near the soil surface at depth dT0 cm.
To investigate the accuracy of the observed data, Table 3 describes the heat balance relationship of observed at the tested sites that expressed in the heat flux. The
![]()
Table 1. Feature of the tested sites (all sites active core measurement presently being made).
![]()
![]()
Table 2. Measurement instruments of the tested sites including dT0.
imbalance was estimated by ![]() using observed annual data and the imbalance ratio defined as
using observed annual data and the imbalance ratio defined as![]() . There are numerous data gaps at all sites on an hourly basis.
. There are numerous data gaps at all sites on an hourly basis.
3. Result
3.1. Conversion of Observed Data (Hobs and lEobs) into Corrected Data (Hcor and lEcor)
The observed data do not achieve the heat balance relationship shown in Table 3. To maintain the heat balance, multiple regression analysis is applied using Equation (8) as aforementioned. Figure 3 describes the relationship (Rn − G) versus (H + lE) of the original and corrected data at all tested sites. The observed data are shown in the red circle, whereas the corrected data are shown in the blue circle. The slope of the corrected data at the tested sites mostly increased and approached 1.0 [1] [2] .
The regression coefficients for all tested sites are described in Table 4 that A is for lE and B is for H. The correction coefficient A ranged from 0.836 to 1.495 for H, with an average of 1.130, and the coefficient B ranged from 0.950 to 1.312 for H, with an average of 1.157. The observed data are corrected using these coefficients for all tested sites. The imbalance ratio Raimb before and after correction is described in Table 3.
![]()
Table 3. Annual heat balance relationship of the tested sites (except no observed data): Data gap, one of which G, Tz, T0, P (atmospheric pressure), rehz, Rn, Hobs and lEobs, is do not use for analysis. Imbalance is calculated by ![]() using yearly observed data and the imbalance ratio defined as
using yearly observed data and the imbalance ratio defined as![]() .
.
![]()
Table 4. Regression coefficients A for lE and B for H: Regression coefficient is the same with correction coefficient of observed H and lE.
![]()
![]()
![]()
Figure 3. Relationship between (Rn − G) versus (H + lE) (W・m−2): According to the heat balance relationship, Rn + G = H + lE must be guaranteed by actual data. Therefore, Rn + G versus H + lE compared. But Rn + G does not coincide with H + lE as red circle in the figure, to improve the relationship, regression analysis performed. The blue circle indicates the result of the regression analysis at eight tested sites.
3.2. Result of the General Solution by Equation (9) and Equation (10)
We set the initial value as Ts = T0 and rehs = rehz based on the triangle concept in Figure 2 as aforementioned. According to the initial values, the heat balance relationship is initially almost satisfied. The constraints Equation (15) applied for all sites except FR- Lam and CN-QHB because these two sites having relatively large amount of precipitation. This reason describe in the discussion section.
The estimation of Ts and rehs is conducted with precision = 0.000001 and convergence = 0.0001 in Solver option. In addition, heat balance is not achieved instantaneously; it requires a few hours [3] . Thus, the figure adjusts to a five-hour moving average. The comparison procedure is similar to the previous research [1] [2] .
3.3. Comparison of the Hourly Change of lE and H Estimated and Corrected
To confirm the validity of the general method, Figure 4 compares the hourly change in lEcor with lEest and Hcor with Hest at all sites in summer. All sites are very well consisted with each other. However, in detail, lEest is not consistent with lEcor at US-Dia and Hest is
![]()
![]()
Figure 4. Hourly change of lE and H observed and estimated at the tested sites by general method (1) (W・m−2): The left hand sites describe the comparison of estimated and corrected lE and right hand side describe the estimated and corrected H at all tested sites.
not consistent with Hcor at FR-Lam. In the former case, lEest is overestimated, while Hest is underestimated. The other items, such as lEobs and lEimb, indicate almost similar trends, and Hobs and Himb also show the same trend but with small differences (not shown).
3.4. Annual Change of the Estimated and Observed lE and H
To investigate annual change in the estimated and observed lE and H, Figure 5 describes the changes of those variables throughout the year. All sites describe the trend is relatively well reproduced.
However, in detail, at AU-Dry and AU-Stp, lEest indicate underestimate at former part of the year while Hest the overestimate at the same period. At FR-Lam, lEest indicate a little underestimate at the year while Hest are a little overestimate. The other items of lEobs and lEimb exhibit similar trends, and Hobs and Himb also display the same trend but with small differences (not shown).
3.5. Comparison of the Observed and Estimated lE and H
To confirm the validity of the general solution (1), Figure 6 compares the observed versus estimated data of lE and H on a daily basis. If the slope (slope of the straight line) is 1.0, the observed value coincides well with the estimated value. For H, the slopes of the observed versus estimated relationship nearly coincide (<15%) at the all sites except AU-Dry. For H, all sites indicate underestimate (>15%). R2 values (determination coefficient) shows a small values (<60%) for all sites except US-Dia (0.815) and AU- TTE (0.822), US-Whs (0.745). The other items of lEobs and lEimb are exhibited similar trends, and Hobs and Himb show the same trend but with small differences (not shown). In addition, boundary of estimation accuracy is selected as 15% by referring the heat imbalance of original data.
![]()
![]()
Figure 5. Annual change of lE and H estimated and observed by general method (1) (W・m−2): The left hand sites describe the comparison of estimated and corrected lE and right hand side describe the estimated and corrected H at all tested sites.
3.6. Comparison of the Observed rehz with Estimated rehs and T0 with Ts
The relationship between the estimated rehs and the observed rehz, i.e., the initial values and converged values, is of great concern. The left hand side of Figure 7 describes the hourly changes of those two items in summer. The parameters exhibit quite similar trends, i.e., the difference between rehs and rehz is quite small. The right hand side of Figure 7 describes the change of Ts − T0 and Ts − Tz. T0 is the observed temperature near the soil surface, and Tz is the air temperature, as previously mentioned. Ts − T0 changed periodically with daily changes about ±3˚C with site specific but sometimes shows a large difference. The difference between Ts − Tz is approximately within 8˚C.
The above trend of rehs and Ts changes is quite similar in the other seasons and at the other sites, although small differences are observed (not shown). In addition, the discontinuous portion is originated from data gap.
3.7. Comparison of Estimated and Observed Evapotranspiration Rate (ETa)
Using observed and estimated lE, monthly evapotranspiration was obtained at the all sites, as shown in Figure 8 by assuming 100 W・m−2 equivalents for 3.53 mm・day−1 [15] . The initial value of rehse quals rehz and constrains as Equation (12) and Equation (15) was applied. In addition, if there are data gap in a given month, the average ETa in a day multiplied the number of days of the month.
All sites describe satisfactory well reproduced Ha and Eta except AU-Dry. In detail, although there are small differences between Haobs, Hacor and Haest, and also ETaobs, ETacor, and ETaest at all sites, the difference was relatively small.
![]()
![]()
Figure 6. Comparison of lE and H estimated and observed at the tested sites by general method (1) (W・m−2).
Relative humidity at US-AR2 (2010) Ts-Tz and Ts-To at US-AR2 (2010)
![]()
![]()
Figure 7. Hourly change of relative humidity and temperature observed and estimated at the tested sites by general method (1) (˚C): The left hand sites describe the comparison of rehs and rehz and right hand side describe the temperature difference Ts-Tz and Ts-T0 at all tested sites.
4. Consideration
4.1. Comparison of General Method (1) with Conventional Method
The conventional method using Equation (3) cannot uniquely determine both Ts and rehs because two variables can’t determine mathematically by one equation. However, our aim of this analysis is to determine reasonable lE and H values for conserving the heat balance relationship. If we attempt to determine reasonable lE and H values using one equation, optimization can be performed by adjusting either Ts or rehs to satisfy the relationship. Based on the concept, the following analysis is conducted under initial values of Ts = Tz and rehs = rehz with the constraint of 0 < b < bmax. Table 5 compares the slope of lEest and Hest against lEcor and Hcor (as Figure 6) for general method (1) as well as conventional method.
For Hcor, the general method (1) is almost the same accuracy with the conventional method in that the slopes of all sites are adequate range (1.0 ± 0.15), while for lEcor, all sites under estimate (<0.85). However, conventional method more balanced from the slope of lEcor and LEcor. In addition, the figures as Figure 4 to Figure 8 in general method (1) that previously described are quite similar those of the conventional method, therefore, the figures abbreviated because of space limitation. In addition, the accuracy criteria (1.0 ± 0.15) determine conventionally referring to observed data accuracy (Table 3).
![]()
Table 5. Comparison of the slope with corrected against estimated for general method (1), conventional method and general method (2): General method (1) estimates Ts and rehs using simultaneously two equations as Equation (9) and Equation (10), which guaranteed the uniqueness of variable determination, while conventional method estimate Ts and rehs using Equation (3) only which not guaranteed the uniqueness of variable determination. General method (2) used Ts observed by radiometer and rehs determined by Equation (13), thus, guaranteed the uniqueness of variable determination.
Note: *indicate accuracy; (1.0 ± 0.15).
4.2. Comparison of General Method (1) with General Method (2) Using Ts Observed by Radiometer
To verify the validity of our method, estimation lE and H using observed Ts (Tsrad) by radiometer is performed. By using the Ts, the lE and H can be determined uniquely by Equation (1) to Equation (3) using Tsrad instead of Tsass because the unknown variable is only one. The result described in Table 5 in that this method almost the same accuracy those of conventional method and more balanced Hcor and lEcor. In addition, the result as Figures 4-8 in general method (1) previously described are quite similar those of this method. Therefore, the figures abbreviated because of space limitation.
4.3. Comparison of Total Amount of Yearly Ha and ETa of Three Methods
To compare the total amount of sensible heat (Ha) and latent heat flux (ETa) estimated and corrected expressed in mm・year−1 base. The estimation of Ha and ETa performed three ways as general method (1), conventional method and general method (2). The results summarized in Table 6.
Table 6 describes that the estimated Ha and ETa by the three methods mostly reproduced the corrected Ha and ETa. But there are site specific and method specific difference. Among this, general method (2) is seemed to be mostly suitable because which more coincided with the Hacor and ETacor. However, the data of Tsrad is rarely at common climate observation, thus, we focused on general method (1) and conventional method.
![]()
Table 6. Comparison of corrected Ha and Eta versus estimated Ha and Eta of various method (mm・year−1): General meth. (1), conventional meth. and general meth. (2) refer to the caption of Table 5. Unit of heat flux (W・m−2) converted to (mm・day−1) as ratio of 100 (W・m−2) is equivalent for 3.53 (mm・day−1) [15] . FR-Lam and CN-QHB does not apply b > 0.
Note: second row of each sites indicate the ratio against observed (corrected) data. Note: *indicate the accuracy; (1.0 ± 0.15). Note: observed data obtained by general solution (1).
To make clearer the accuracy, the annual Ha and ETa, compared as the ratio of estimated Haest and ETaest against corrected Hacor and ETacor. Which shown in second row of each sites in Table 6 because the corrected data is a standard of reasonable estimation.
Attached star indicate the accuracy range (1.0 ± 0.15). For general method (1), most of Haest/Hacor indicated (1.0 ± 0.15) except FR-Lam while over half sites of ETaest/ETacor indicate out of (1.0 ± 0.15). For conventional method, most of Haest/Hacor, indicate under 0.15 except AU-dry and FR-Lam while ETaest/ETacor all sites indicate under 0.15 except US-Dia and AU-TTE where are belong to arid region. For general method (2), Haest/Hacor and ETaest/ETacor at three sites indicate (1.0 ± 0.15) but AU-TTE and AU-Dry and FR-Lam of Haest are out of (1.0 ± 0.15). All of the above data describe mostly reasonable against our proposed method, although there are some exceptions.
4.4. Comparison of ETa versus Precipitation from the Aspect of Water Balance
It is considered that annual precipitation almost consumed as ETa in arid and semi- arid region. Figure 9 describes the relationship of annual precipitation versus ETacor and ETaest by general method (1). Both figures describe mostly consistent each other. The facts indicate the reasonability of our proposed method from the aspect of water balance.
![]()
Figure 9. Comparison of ETacor and ETaest versus precipitation.
5. Discussion
5.1. Effect of Constraints “b” on lE/H Ratio
The constraint expressed by Equation (15) is very well functioned for estimation of lE and H in arid region as US-Dia and AU-TTE having annual precipitation 297 mm and 180 mm. If the constraint does not apply at AU-TTE, for example, slope of lEest/lEcor is 1.552, while Hest/Hcor is 0.586 (not shown in figure or table). But if it applied the constraint at the same site, the slope of lEest/lEcor is 0.721 while Hest/Hcor is 0.904, resulting in remarkably improved. Apparent meaning of the constraint is almost rehs < rehz, but if the constraint applied directly the Hest and lEest do not achieve optimal value smoothly.
Moreover, this constraint does not well functioned at semi-arid region having relatively large amount of precipitation as FR-Lam and CN-Hab. Therefore, the two sites do not apply the constraints. The other sites as AU-Dry, AU-Stp, US-Ar2 and US-Whs are intermediate of above sites. If the constraint applied, the Hest are well estimated while if do not applied the lEest are well estimated.
5.2. Exceptions of the Abnormal Fluctuation in Convergence Process
In convergence process, The Hest and lEest sometimes fluctuate plus or minus abnormally because sum of those is limited (=Rn + G). For example, the former estimate abnormally large (plus) while the latter abnormally small (minus). To avoid the abnormal fluctuation, constraint as ABS (Rn + G) < H or lE is applied. On the other hand, observed data contain sometime the abnormal data that appear at near 0˚C in winter season or early morning. The analyses were conducted without the abnormal data [1] [2] .
6. Conclusions
In the natural world, air temperature and humidity reflect the partitioning of the sensible and latent heat flux from Rn and G. Based on the concepts, we attempt to reciprocally estimate the H and lE from Rn and G. By applying the Bowen ratio concept to the soil surface, the unknown variables Ts and q(Ts), i.e., rehs, are estimated by an optimization procedure satisfying the heat balance relationship [1] [2] .
This method is very effective to expand the utility of the water recourses issues through estimation of evapotranspiration for various areas because it requires only single height Tz and rehz that are very popular climate elements.
The validation of the method was conducted using eight globally dispersed sites, where observed lE and H by the eddy covariance using FLUXNET. The analysis was conducted on an hourly basis and was summarized as daily averages.
The analysis was conducted using three methods, namely, the general (1), conventional and general (2) methods. The general method (1) is based on the unified determination of Ts and rehs by solving two heat balance equations simultaneously, whereas the conventional method is based on solving a single heat balance equation that does not unify Ts and rehs. The general method (2) is based on Ts observed by radiometer.
The general method (1) is mathematically reasonable, but the data of two unit times are required. The conventional method does not allow for the uniqueness of Ts and rehs, but reasonable partitioning of H and lE can be achieved by adjusting either Ts or rehs, depending on the GRG algorithm. The main purpose of our research is to accurately estimate lE and H rather than to accurately estimate Ts and rehs; thus, the conventional method can be used as well as the general method (1). If Ts observed by radiometer, application of the general method (2) is reasonable.
The main validated results are as follows:
1) The observed data are corrected by regression analysis because it does not guarantee the heat balance relationship.
2) The general and conventional solutions are nearly consistent for hourly changes of lEest with lEcor as well as Hest with Hcor at eight sites. However, there are some site- specific differences.
3) The general and conventional solutions are nearly consistent for the annual changes of lEest with lEcor, and Hest with Hcor at eight sites. However, there are some seasonal and site-specific differences.
4) Analysis of annual change of Ha and ETa are performed. The results describe that Haest is consistent with Hacor and ETaest consistent with ETacor.
5) To confirm the reasonability of general method (1), conventional method and general method (2), the ratio of ETaest/ETacor is compared. The result indicates that there is no remarkable difference among the two methods.
6) Annual precipitation is mostly consistent with ETaest and ETacor from the aspect of water balance.
The estimated results do not completely reproduce the observed data, but the results are mostly satisfactory for the estimation of lE and H. The remarkable feature of this method is that it is applicable for single height of temperature and humidity with Rn and G. This feature shows the method would be widely applicable for estimation of lE. If this procedure is approved widely, the resolution of water resources problem and reasonable irrigation planning will be more advanced.
However, there are some issues to be solved in future: 1) Error plain of ε in Equation (3) or Equation (9) and Equation (10), i.e., relationship of ε with Ts and rehs, is very complicated, having many local minimum. Therefore, the importance of determination of initial values is still important; 2) Applying constraint is also important issues because it strongly affects the results; 3) Snow and frozen problems are not considered in this research so that these problems should be solved in future and 4) Accuracy of the observed data is also very important issue which has been improved nowadays by many researchers and technologists.
We conclude that ET and H are controlled by energy conservation in nature. Realistically, the observed temperature and humidity are strongly affected by the partitioning of H and lE and vice versa. Therefore, using the observed temperature, humidity and common climate elements, lE and H values are reciprocally approximated by the optimized techniques [1] [2] .
Acknowledgements
We express sincere thanks to the AmeriFlux,EuroFlux and AsiaFlux principal investigation for data accessed July 5, 2015. We thank Dr. Fujihara Yooich and Dr. Takimoto Hiroshi for providing valuable comments for the optimization procedure. We acknowledge the following AmeriFlux sites for their data records: site IDs. In addition, funding for AmeriFlux data resources was provided by the U.S. Department of Energy’s Office of Science.
Appendix 1
The GRG Nonlinear Solving Method for nonlinear optimization: developed by Leon Lasdon (University of Texas at Austin) and Alan Waren (Cleveland State University) and enhanced by Frontline Systems, Inc.
For more information about the other solution algorithms, advice on building effective solver models, and solving larger scale problems, contact: Frontline Systems, Inc.
Web site: http://www.solver.com, E-mail: info@solver.com
Eestimated results have not completely reproduced the observations, but the results are mostly satisfaction
Appendix 2
Using modules of Visual Basic for Applications (VBA) in the manuscript
Sub Macro “Number1 ( )
' Macro ”Number 1”:GRG method
Dim r As Long
Dim lastRow As Long
lastRow = Range(“〈Column Alphabet〉” & Rows Count).End (xlUp).Row
SolverReset
For r = 〈Start row number〉To〈End row number〉
SolverReset
SolverOptions Precision:=0.000001, Convergence:=0.0001, StepThru:=False, Scaling:=False _
, AssumeNonNeg:=False, Derivatives:=2
SolverOkSetCell:= "Row" & r, MaxMinVal:=2, ValueOf:=0_
, ByChange:=Range(Cells(r, 〈First column number〉), Cells(r, 〈Last column number〉))
SolverAddCellRef:="$ 〈rehs’s Column Alphabet〉" & r, Relation:=1, FormulaText:=1
SolverAddCellRef:="$ 〈rehs’s Column Alphabet〉" & r, Relation:=3, FormulaText:=0
SolverAddCellRef:="$ 〈RTs’s Column Alphabet〉" & r, Relation:=1, FormulaText:=5
SolverAddCellRef:="$ 〈RTs’s Column Alphabet〉" & r, Relation:=3, FormulaText:=-5
SolverAddCellRef:="$ 〈Hestimated’s Column Alphabet〉" & r, Relation:=1, FormulaText:= "$ 〈Rn-G observed’ s Column Alphabet〉$ &r
SolverAddCellRef:="$ 〈Hestimated’s Column Alphabet〉" & r, Relation:=3, FormulaText:=-100
SolverAddCellRef:="$ 〈LEestimated’s Column Alphabet〉" & r, Relation:=1, FormulaText:= "$ 〈Rn-G observed’ s Column Alphabet〉$ &r
SolverAddCellRef:="$ 〈LEestimated’s Column Alphabet〉" & r, Relation:=3, FormulaText:=-100
SolverAddCellRef:="$ 〈Bapp’s Column Alphabet〉" & r, Relation:=1, FormulaText:=100
SolverAddCellRef:="$ 〈Bapp’s Column Alphabet〉" & r, Relation:=3, FormulaText:=-100
※in case of 0
max
SolverAddCellRef:="$ 〈bestimated’s Column Alphabet〉" & r, Relation:=3, FormulaText:=0
SolverAddCellRef:="$ 〈bestimated’s Column Alphabet〉" & r, Relation:=1, FormulaText:= "$ 〈bmax’ s Column Alphabet〉$ &r
SolverSolveUserFinish:= True, ShowRef:="DummyMacro"
Next
End Sub
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact ojmh@scirp.org