Non-Local and Memory Character of Frictional Energy Dissipation on Atomic Scale ()
1. Introduction
The problem of friction is of enormous practical importance. However, fundamental understanding of the origin of dissipative surface forces on microscopic level is still far from being satisfactory. Only recently, with the application of atomic force microscopes to friction (friction force microscopy―FFM) atomic- scale access has been acquired to the origin of dissipative surface forces, boosting the rapidly developing field of nanotribology [1] [2] [3] .
There are many physical parameters which can be important for atomic scale friction, but two of them seem really crucial. One is the corrugation of the effective (mean force) contact potential: the lateral barriers faced by the slider are responsible for the appearance of stick-slip motion and sizable friction experienced. The other is the inherent dissipation rate, which describes how rapidly the energy invested into the system is losing irretrievably to the outside world. These two key parameters are never known in advance, not only because of uncontrolled contact conditions but also in view of nontrivial physics involved. This is in contrast to practically all other system parameters, which can be taken directly from experiments (like mass and flexibility of the tip and cantilever) or reasonably estimated. In our earlier work [3] [4] we have shown how FFM experiments can be analyzed in a consistent way in spite of the lack of initial knowledge with respect to the contact potential corrugation. In this work we concentrate on some hidden problems concerned with the dissipation rate.
The traditional description of atomic-scale friction in terms of mechanical stick-slip instabilities appears so successful that it obscures the actual mechanisms of energy dissipation. The reason is that the observed friction force in the stick-slip regime is nearly completely determined by the system parameters (flexibility and contact potential corrugation) and it is practically independent of the dissipation rate, provided the latter is constrained to a certain range, the origin of which has never been explained. As was shown in our recent works [3] [5] [6] [7] , there are at least two hidden problems.
The mere fact that atomic stick-slip patterns are readily observed in experiments implies that the inherent dissipation rate is close to the characteristic frequency of the measuring system (nearly critical damping). Similar assumption is needed to explain some more subtle aspects of sliding dynamics, like the rare occurrence of long slips. Although nearly critical damping is suggested by experiments, it is absolutely unclear what could be physical reasons for that. Moreover, it seems to defy common sense. Indeed, it implies that the dissipation rate is mainly determined by the characteristic frequency (i.e. by the flexibility and mass) of the measuring system but it is only weakly dependent on the contact conditions and the substrate where energy is dissipated. Certainly, one would expect just the opposite.
Another problem is due to the observation that the typical (nearly critical) value of the dissipation rate needed to explain FFM experiments turns out to be several orders of magnitude higher than we can expect on the basis of data collected for surface diffusion (see, e.g., [8] ) of atomic particles and clusters and related phenomena.
These observations force us to critically reconsider traditional views on frictional energy dissipation. In what follows, we propose that the hidden problems of atomic scale friction find their origin in the nontrivial character of the dissipation that is non-local and dominated by memory effects, which?as far as we know?have not been addressed before in the context of dry, atomic-scale friction.
2. Dissipative Surface Force
In the theory of atomic scale friction (see, e.g., review papers [2] [3] ), one traditionally uses familiar Langevin equation of motion for the slider (the FFM tip) assuming that the dissipative force experienced is linear in its velocity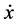 , with constant damping factor η (the dissipation rate),
, with constant damping factor η (the dissipation rate),
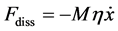 (1)
(1)
(mass M of the moving object is introduced here by formal reasons to provide η with the convenient dimensionality of frequency). In view of the fluctuation- dissipation theorem, this implies that thermal noise is white (δ-correlated) and memory effects can be neglected. The force (1) is sometimes called viscous force, by a formal analogy with Stock’s force in liquids, but actually this analogy is poor. To our knowledge, however, the applicability of this approximation to dry friction has never been properly justified. In fact, the above mentioned problems (i.e. too a high value of η and its closeness to the characteristic frequency of the measuring system, as follows from FFM experiments) indicate that the traditional approach (1) is strongly oversimplified.
To clarify the question, we first address some general statements of Non- equilibrium statistical mechanics, see, e.g., [9] [10] . The dissipative and random forces appear in a natural way when one goes over from full description of a multi-particle system to a reduced description, when one is interested in the evolution of only one particle or one degree of freedom (in our case this is the position of the slider or FFM tip at the solid surface) averaged over all other degrees of freedom of the system which serve as a bath. Generally, such a reduction can be accompanied by a renormalization of mass and bare potentials, and by the appearance of entropic effects. The dissipative (Fdiss, sometimes called friction) and random (Fran) forces experienced by the particle are due to the dissipation of the particle’s energy and momentum to the substrate bath and thermal fluctuations in the bath, respectively. Fdiss is not necessarily linear in the particle’s velocity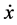 , but―importantly?it depends on entire history of the system,
, but―importantly?it depends on entire history of the system,
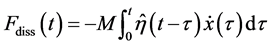 (2)
(2)
with 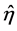 the memory kernel. This manifests a natural fact that the force experienced at a certain moment of time depends on how energy and momentum have been invested to (or retrieved from) the substrate at previous moments of time. As a manifestation of the fluctuation-dissipation theorem, the memory function is directly related with the noise correlation function,
the memory kernel. This manifests a natural fact that the force experienced at a certain moment of time depends on how energy and momentum have been invested to (or retrieved from) the substrate at previous moments of time. As a manifestation of the fluctuation-dissipation theorem, the memory function is directly related with the noise correlation function,
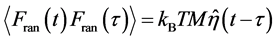 (3)
(3)
with 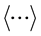 denoting statistical averaging, T temperature and kB the Boltzman constant.
denoting statistical averaging, T temperature and kB the Boltzman constant.
The familiar approximation (1) corresponds to the limiting case when, by some reasons, the random force correlations are extremely short and memory effects can be neglected, so that
 (4)
(4)
If memory effects are important, the usage of the traditional linear approximation (1) inevitably implies that the description is coarsened, i.e. averaged over certain time intervals τ*. In this case the damping factor in (1) has the meaning of mean dissipation rate,
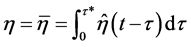 (5)
(5)
In the stick-slip regime of FFM friction, the characteristic time intervals are related with the period of the tip vibration in a surface potential well, which, in turn, is directly related with the flexibility and mass of the measuring system. This can provide a clue [5] to understanding the origin of nearly critical damping.
With very few exceptions [2] [5] , the question of the possible role of memory in dry, atomic scale friction has not been touched in the literature. One could think that the assumption of δ-correlation of random forces and, hence, the applicability of the traditional approximation (1) is justified because, typically, the time scales associated with excitations (phonon or other) in the solid are short compared to the motion of the slider from one surface potential minimum to another. Apparently, such an argument would tacitly imply that, as one might think, the dissipation is local, i.e. irretrievable loss of the particle energy and momentum takes place in the slider?surface contact region. This would mean that atoms in the bulk of the solid do not contribute to friction, although some works indicated the opposite [11] . Our statement is that dissipation is of an essentially non-local character and the memory effects play a principal role, at least when dissipation to phonon bath is concerned.
3. Phononic Mechanism of Dissipation
For solid systems, it is suggested to use the advantage of the normal mode presentation for vibrational degrees of freedom. Considering the evolution of a particle (or a system of particles) interacting with a solid, one can start with the full system of dynamical (Newtonian) equations of motion for the particle(s) and for all atoms in the solid. The equations are coupled, in view of interatomic interactions. Rewritten in terms of normal phonon modes, equations of motion for the solid in harmonic approximation (when there is no direct coupling between phonon modes) turn out to be relatively simple in their form and they can be formally solved analytically, for given positions of the particle under interest at current moment of time and in the past. After substituting the solutions into the equation of motion of the particle, the later can be reduced to generalized Langevin equation with memory, with the dissipative force of the form (2) and random force obeying the fluctuation-dissipation theorem (3). Such a procedure has been used in a number of works [12] [13] [14] in application to various physical problems. Here, we explore some results of our own derivation [15] performed in application to the problem of atomic scale friction.
An important conclusion of this derivation is that the non-retrievable loss of the particle’s energy and momentum is not only due to atoms in the close vicinity to the contact, as one could think, but also atoms in bulk of the solid contribute to friction significantly. Notice that earlier the role of bulk solid atoms was anticipated [11] on the basis of numerical calculations that revealed dependence of friction force on the number of atomic layers in the substrate. In fact, an essentially non-local character of phononic energy dissipation can be seen explicitly and rigorously. Another nontrivial and essentially new conclusion is concerned with mechanism of the dissipation. It can be shown that the appearance of friction force at low velocity is directly related with damping of induced motion (of the mean positions) of atoms in the solid.
These conclusions are general as they do not need any specification of interatomic interactions and structure of the solid. More detailed analysis is cumbersome and it will be addressed elsewhere [15] . Instead, here we propose a simple atomistic model that allows to elucidate the origin of non-locality and memory, and explains the problem of nearly-critical damping in FFM.
4. The Model of Dynamical Deformation Pattern
Our approach is based on the concept of a dynamical deformation pattern. When an object (the tip apex) is in contact with the surface, there is a certain deformation of the substrate lattice. This deformation pattern follows the object upon its motion along the surface. Dynamical deformation of the lattice is an essentially dissipative process, as it is accompanied by the creation of phonons. Such is, in particular, the known mechanism of attenuation of low frequency sound in solids [16] . In accordance with the general conclusion of the previous paragraph, this is also the possible way to treat the phononic mechanism of frictional energy dissipation. In this picture, energy dissipates not due to motion of the object with respect to the surface but due to the motion of the object together with the related dynamical deformation pattern (DDP) with respect to ideal non-deformed lattice. In other words, the dissipation is related with damping of the induced motion of solid atoms which are currently involved into the DDP.
At first glance, the effective size of DDP can seem very small, since the (static) deformation of the substrate lattice rapidly decays with distance n from the contact (in units of atomic spacing a), basically as n−2 when na is large compared to the contact size. However, the number of solid atoms at distance n from the contact scales as n2, and hence these two trends are to compensate each other. Consequently, DDP can be―in principal―very large, and its actual effective size should be determined by some other reasons. Apparently, this is the system history that determines which atoms of the solid have already been involved in collective motion with the slider and which not. The picture can be essentially different depending on type of the slider motion, e.g. for its translational motion along the surface and for an oscillatory one. In this paper we concentrate at the latter, since it is just the case directly related with FFM measurements.
5. Explanation of Nearly-Critical Damping
In the stick-slip regime, the FFM tip vibrates in a surface potential well and slips to the neighboring (typically) well at a critical value of the external force exerted by the cantilever [1] [2] [3] . Dissipation of mechanical energy takes place in the slip events, which can still be considered as damped oscillations with large amplitude, rather than translational motion. (Purely translational motion is realized in a low friction regime of so called “superlubricity” which is of less interest.) Strictly speaking, there are at least two modes of vibrations [3] [17] , one concerned with rapid motion of the tip apex with respect to the tip’s center of mass and the other related with much slower motion of the tip together with the cantilever. The problem of critical damping, as discussed in Introduction, is related with the rapid mode. Damping of the slow mode is not essential [6] for the friction force measured in FFM, but it can also be controlled in experiments [18] .
The problems are met in the framework of the traditional?coarsened? description (1) when η should be treated as the mean dissipation rate (5). Now our task is to estimate it taking explicitly into account the non-local and memory character of dissipation.
For an oscillator with frequency νos the dynamical deformation pattern includes atoms which have been involved in concerted motion during halve the period of its vibration. The effective radius (nmax) of DDP can be estimated as the distance travelled with sound velocity c during this time interval, nmax ~ c/(2νosa). For typical frequency much smaller than the atomic frequency, 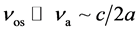 , the effective size of DDP turns out to be large compared to the contact size (which is implied atomically small). Assuming that the characteristic induced velocity
, the effective size of DDP turns out to be large compared to the contact size (which is implied atomically small). Assuming that the characteristic induced velocity 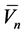 of an atom at distance n from the contact is proportional to the relative static deformation of the lattice at that distance, it can be estimated as
of an atom at distance n from the contact is proportional to the relative static deformation of the lattice at that distance, it can be estimated as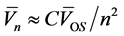 , with
, with 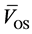 the mean velocity of the oscillator and with factor C of the order of unity which depends on normal load and accounts for the degree of the lattice deformation in the close vicinity to the contact. Since atomic motion in the solid is effectively damped on the time scale of the inverse atomic frequency
the mean velocity of the oscillator and with factor C of the order of unity which depends on normal load and accounts for the degree of the lattice deformation in the close vicinity to the contact. Since atomic motion in the solid is effectively damped on the time scale of the inverse atomic frequency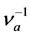 , atom of mass ma moving with induced velocity
, atom of mass ma moving with induced velocity 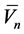 experiences a dissipative force
experiences a dissipative force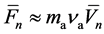 . Calculating the mean dissipative force experienced by the slider as sum over the forces acting on all atoms in DDP,
. Calculating the mean dissipative force experienced by the slider as sum over the forces acting on all atoms in DDP, 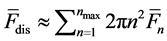 , one obtains
, one obtains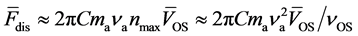 . Expressing frequencies νa and νos in terms of masses and stiffness of the corresponding springs, and introducing the mean dissipation rate for the oscillator,
. Expressing frequencies νa and νos in terms of masses and stiffness of the corresponding springs, and introducing the mean dissipation rate for the oscillator, ![]() , according to equation
, according to equation![]() , one finally obtains
, one finally obtains
![]() (6)
(6)
with ka the characteristic stiffness of atomic bonds and Kos stiffness of the oscillator spring.
Physics behind the result (6) seems clear: the oscillator frequency νos simply determines the rate with which the system delivers mechanical energy to the contact, while the dimensionless factor Cka/KOS determines the part of energy which is invested into the substrate. The absence of any other physical parameter in (6) reflects the fact that at velocities small compared to sound velocity, ![]() , solid acts as an ideal dissipater. One can also notice that the result (6) looks similar to what was obtained by us earlier [5] using a ‘naive’ model when dissipation was related with generation of a sound wave in the solid, with frequency νos. In fact, this similarity is remarkable, since halve wave length of such a wave corresponds to the effective size of DDP considered above.
, solid acts as an ideal dissipater. One can also notice that the result (6) looks similar to what was obtained by us earlier [5] using a ‘naive’ model when dissipation was related with generation of a sound wave in the solid, with frequency νos. In fact, this similarity is remarkable, since halve wave length of such a wave corresponds to the effective size of DDP considered above.
Although the estimates performed are simple, they capture the basic aspects of non-local and memory character of frictional energy dissipation, and they lead to a principal result. Expression (6) reveals direct coupling of the (mean) dissipation rate with the slider frequency, thus explaining the paradox of critical damping. Moreover, the obtained value of ![]() is in excellent agreement with experimental observations. Typical stiffness of FFM tip apex is usually of the order of ka (~1 N/m), so that damping of the rapid FFM mode with KOS ~ ka is predicted by (6) to be close to or somewhat smaller than critical (by definition ηcrit = 4πν). This is just what is needed to explain atomic periodicity of FFM scans and the rare occurrence of long slips [5] [6] [7] [19] . Notice that C in (6) should increase with increasing lattice deformation and this is in correspondence with the load dependence of the dissipation rate concluded from observations of long slips [19] . As far as damping of the slow FFM mode is concerned, it is predicted by (6) to be about two orders of magnitude lower than critical, implying typical value of cantilever stiffness of about a hundred of N/m. This turns out to be in full agreement with a cantilever Q-factor measured in experiments [18] .
is in excellent agreement with experimental observations. Typical stiffness of FFM tip apex is usually of the order of ka (~1 N/m), so that damping of the rapid FFM mode with KOS ~ ka is predicted by (6) to be close to or somewhat smaller than critical (by definition ηcrit = 4πν). This is just what is needed to explain atomic periodicity of FFM scans and the rare occurrence of long slips [5] [6] [7] [19] . Notice that C in (6) should increase with increasing lattice deformation and this is in correspondence with the load dependence of the dissipation rate concluded from observations of long slips [19] . As far as damping of the slow FFM mode is concerned, it is predicted by (6) to be about two orders of magnitude lower than critical, implying typical value of cantilever stiffness of about a hundred of N/m. This turns out to be in full agreement with a cantilever Q-factor measured in experiments [18] .