Effect of Resonance on the Motion of Two Cylindrical Rigid Bodies ()
1. Introduction
Russel [4] studied the motion of two spherical rigid bodies. In same way, Kopal [5] extended the previous work of Russel [4] ; Cowling [6] , Sterne [7] and Brouwer [8] generalized the work of previous authors by considering the lean angle and eccentricity as the small quantities. Johnson and Kane [9] extended the work of above authors by imposing some axiomatic restrictions as follows:
1) The inertia ellipsoids of two rigid bodies 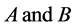 for their respective mass centre
for their respective mass centre 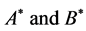 are ellipsoids of revolution.
are ellipsoids of revolution.
2) Either the distance between 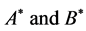 is considerably greater than the greatest dimension of either body or the ellipticities of the inertia ellipsoids of
is considerably greater than the greatest dimension of either body or the ellipticities of the inertia ellipsoids of 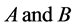 are small.
are small.
3) The angular velocities of 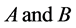 in an inertial frame of reference
in an inertial frame of reference 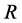 are initially parallel to the symmetrical axes of
are initially parallel to the symmetrical axes of 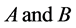 respectively.
respectively.
4) The mass centers 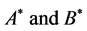 move in plane whose orientation is fixed in
move in plane whose orientation is fixed in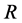 .
.
Bhatnagar [3] , Elipe and Miguel [10] , Choudhary and Mishra [11] , Mercedes and Elipe [12] have discussed the problem similar to the works of the author of early thirties and forties. But Milution Marjanov [13] has discussed the problem on the cause of resonant motions of celestial bodies in an inhomogeneous gravitational field. He has shown that, when eccentricities of the orbits differ from zero and cross section of the ellipsoids of inertia with orbital plane differs from the circle, the two-cycle resonance is the most stable one. Further Milution Marjanov [13] has discussed the effect of resonance on the problem of two real bodies. He has shown that there are 22 periodic functions and all the variables are coupled. Moreover he established that the stability of the orbit i.e. periodicity of the motion requires 231 resonances.
In our present work, we have proposed to extend the work of Bhatnagar et al. [1] [2] [3] by taking into account the effect of resonance and imposing some modified axiomatic restrictions as follows:
1) The inertia ellipsoids 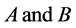 for their mass centers
for their mass centers 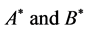 are considered as general ellipsoids only but not the ellipsoids of revolution.
are considered as general ellipsoids only but not the ellipsoids of revolution.
2) The angular velocities of 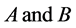 are initially parallel to one of the principal axes, which is perpendicular to the orbital plane of
are initially parallel to one of the principal axes, which is perpendicular to the orbital plane of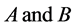 .
.
3) Only the periodic terms are taken and other terms are neglected.
4) The two rigid bodies are symmetrical and cylindrical.
On taking axioms second and fourth under consideration 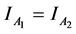 for
for 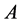 and
and 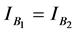 for
for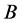 , more critical points are found than that found by Bhatnagar and Gupta [1] [2] .
, more critical points are found than that found by Bhatnagar and Gupta [1] [2] .
2. Equations of Motion
Let 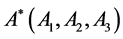 be the mass center of the body
be the mass center of the body ![]() in the rotating frame of reference
in the rotating frame of reference ![]() having a variable orientation in the fixed frame of reference
having a variable orientation in the fixed frame of reference ![]() which is shown in Figure 1. Let
which is shown in Figure 1. Let ![]() be fixed right handed mutually perpendicular axes in
be fixed right handed mutually perpendicular axes in![]() . Let us suppose that
. Let us suppose that ![]() are lines parallel to the principal axes of
are lines parallel to the principal axes of ![]() at
at![]() . We assume that
. We assume that ![]() -plane is normal to the angular momentum of the system about the centre of mass. Let
-plane is normal to the angular momentum of the system about the centre of mass. Let ![]() be the distance between
be the distance between![]() ,
, ![]() be the angle between
be the angle between ![]() and
and ![]() -axis. Let us assume that
-axis. Let us assume that ![]() be the Eulerian angle with the help of the principal axes
be the Eulerian angle with the help of the principal axes ![]() of the body
of the body ![]() at its centre of mass
at its centre of mass ![]() oriented with the fixed axes
oriented with the fixed axes ![]() respectively. Similarly
respectively. Similarly ![]() be the Eulerian angles with the help of the principal axes
be the Eulerian angles with the help of the principal axes ![]() of the body
of the body ![]() at its centre of mass
at its centre of mass![]() , oriented with the fixed axes
, oriented with the fixed axes ![]() respectively.
respectively.
Let ![]() be generalized momenta corresponding to the generalized co-ordinates
be generalized momenta corresponding to the generalized co-ordinates ![]() respectively. Let
respectively. Let ![]() be the principal moments of inertia,
be the principal moments of inertia, ![]() and
and ![]() be the components of the angular velocities of body
be the components of the angular velocities of body ![]() respectively. If
respectively. If ![]() and
and ![]() be the masses of the two cylinders
be the masses of the two cylinders ![]() respectively then the total kinetic energy of the system is given by
respectively then the total kinetic energy of the system is given by
![]() (1)
(1)
where, ![]() kinetic energy of
kinetic energy of ![]() and
and ![]() due to translation.
due to translation.
![]() (2)
(2)
![]() Sum of kinetic energy of
Sum of kinetic energy of ![]() and
and ![]() due to rotation about the principle axes.
due to rotation about the principle axes.
![]() (3)
(3)
If ![]() be the Eulerian angles shown in Figure 1 then the components of angular velocity are given by
be the Eulerian angles shown in Figure 1 then the components of angular velocity are given by
![]() (4)
(4)
Thus the combination of Equations (1), (2), (3) and (4) yields
![]() (5)
(5)
Since for cylindrical bodies ![]() and
and ![]() hence from the Equation (5), we get
hence from the Equation (5), we get
![]() (6)
(6)
The generalized momenta ![]() corresponding to generalized coordinates
corresponding to generalized coordinates ![]() are given by the relations
are given by the relations
![]() (7)
(7)
where, ![]()
i.e. ![]()
![]()
![]()
![]()
![]()
![]()
From![]() , we get
, we get
![]()
![]()
![]()
From![]() , we get
, we get
![]()
Introducing ![]() in the Equation (6), we get
in the Equation (6), we get
![]() (8)
(8)
Following Brouwer and Clemenc [14] the potential ![]() for the two bodies
for the two bodies ![]() is given by
is given by
![]() (9)
(9)
where ![]() is the distance between two elements
is the distance between two elements ![]() and
and ![]() of the two bodies
of the two bodies![]() respectively and
respectively and ![]() is the gravitational constant. The integration extends over total mass of two bodies.
is the gravitational constant. The integration extends over total mass of two bodies.
From Equation (9), we get
![]() (10)
(10)
where![]() .
.
The Hamiltonian function is given by
![]()
where, ![]() unperturbed Hamiltonian
unperturbed Hamiltonian
![]() (11)
(11)
![]() Perturbed Hamiltonian,
Perturbed Hamiltonian,
![]() (12)
(12)
The Canonical equations of motion are given by
![]()
3. Unperturbed Solutions
The Hamilton-Jacobi Equation for the Hamiltonian ![]() is given by
is given by
![]()
The solution of the above equation is given by
![]() (13)
(13)
Hence the solution of the problem can be given in term of the Keplerian elements![]() as
as
![]() (14)
(14)
Here ![]() are the usual Keplerian elements,
are the usual Keplerian elements, ![]() is the eccentric anomaly,
is the eccentric anomaly, ![]() and
and ![]() are constants of integration,
are constants of integration, ![]() and
and ![]() are generalized momenta variables corresponding to
are generalized momenta variables corresponding to ![]() and
and ![]() respectively.
respectively.
4. Approximate Variational Equations Corresponding to Perturbed Hamiltonian
The set of approximate variational equations may be given by averaging the Hamiltonian![]() . The averaged value of the Hamiltonian
. The averaged value of the Hamiltonian ![]() is given by
is given by
![]()
where ![]() is given by the Equation (12).
is given by the Equation (12).
Here, we observe that by averaging the Hamiltonian, short-periodic terms are eliminated from the Hamilton-Jacobi equation. An approximate set of variational equations are given by
![]() (15)
(15)
From the above equations, we get
![]()
From Equation (14), we have
![]() (16)
(16)
Also,
![]() (17)
(17)
![]() (18)
(18)
For solving the Equations (17) and (18), we should know ![]() as function of time.
as function of time.
5. Solutions for Generalized Co-Ordinates
![]() and
and ![]() are generalized co-ordinates.
are generalized co-ordinates.
For the solution, we will use the Lagrange’s equation of motion
![]() (19)
(19)
where ![]() kinetic energy and
kinetic energy and ![]() Potential energy of the system given by the Equations (8) and (10) respectively.
Potential energy of the system given by the Equations (8) and (10) respectively.
From Equation (6), we get
![]()
![]() (20)
(20)
and
![]() (21)
(21)
![]() (22)
(22)
From Equation (12), we have
![]() (23)
(23)
For ![]()
The combination of Equations (19), (20), (21), (22) and (23) gives
![]() (24)
(24)
This is the required Lagrange’s equation of motion in![]() .
.
Again,
![]()
![]()
![]()
Thus the Lagrange’s equation of motion in ![]() is
is
![]()
![]() (25)
(25)
Again,
![]()
![]() (26)
(26)
Similarly for![]() .
.
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
We have assumed that the angular velocities ![]() and
and ![]() of bodies
of bodies ![]() are initially parallel to one of the principal axes which is perpendicular to the orbital plane. If we further assume that no torque (unperturbed motion) is acting on either of the two bodies then both the bodies will spin at a constant rate about that axes and the orientation with the axes will be fixed.
are initially parallel to one of the principal axes which is perpendicular to the orbital plane. If we further assume that no torque (unperturbed motion) is acting on either of the two bodies then both the bodies will spin at a constant rate about that axes and the orientation with the axes will be fixed.
In terms of the Eulerian angles, we have
![]() constant
constant![]() ,
, ![]() constant
constant![]() ,
,
![]() constant
constant![]() ,
, ![]() constant
constant![]() ,
,
![]() constant
constant![]() ,
, ![]() constant
constant![]() ,
,
![]() ,
,![]() .
.
In the case of perturbed motion, let us suppose that
![]() (30)
(30)
where ![]() are the constants corresponding to the torque-free solutions and
are the constants corresponding to the torque-free solutions and ![]() are small quantities which are functions of time.
are small quantities which are functions of time.
Since bodies are cylinders hence
![]() (31)
(31)
where, ![]() radius of body A,
radius of body A, ![]() length of body A,
length of body A, ![]() radius of body B,
radius of body B, ![]() length of body B.
length of body B.
We replace ![]() and
and ![]() by their steady state value
by their steady state value ![]() and
and ![]() respectively and using the Equation (30) and (31) in Equations (24), (25) and (26) and neglecting higher order terms, then from Equation (24), we have
respectively and using the Equation (30) and (31) in Equations (24), (25) and (26) and neglecting higher order terms, then from Equation (24), we have
![]() (32)
(32)
From Equation (25), we have
![]() (33)
(33)
From Equation (26), we have
![]() (34)
(34)
Similarly for the body ![]() using Equations (30) and (31) in Equations (27), (28) and (29), we get
using Equations (30) and (31) in Equations (27), (28) and (29), we get
![]() (35)
(35)
![]() (36)
(36)
From Equation (29), we have
![]() (37)
(37)
Integrating the Equation (36) and putting the value of ![]() in the Equation (37) and neglecting the secular terms, we get
in the Equation (37) and neglecting the secular terms, we get
![]() (38)
(38)
where ![]() are constants independent of
are constants independent of ![]() and
and![]() .
.
Considering Kepler’s equation up to the 1st order approximation![]() , the solution of the Equation (38) is given by
, the solution of the Equation (38) is given by
![]() (39)
(39)
Here we can see that if any one of the denominator vanishes, the motion is indeterminate at the point. It depends on the mean motion and the angular velocity of rotation of the body. There are many points at which resonance will occur but for discussion we have consider only one point ![]() and for other we can use the similar procedure. We further assume that
and for other we can use the similar procedure. We further assume that ![]() is a small quantity and at the equilibrium point
is a small quantity and at the equilibrium point ![]() i.e. mean motion and angular velocity of the rigid body
i.e. mean motion and angular velocity of the rigid body ![]() are in the ratio of 1:2. In order to study the behavior at this point we will follow the procedure of Brown and Shook [15] .
are in the ratio of 1:2. In order to study the behavior at this point we will follow the procedure of Brown and Shook [15] .
6. Resonance at the Critical Points
From right hand side of Equation (39), we have ![]() are the critical points. Here we consider
are the critical points. Here we consider ![]() for discussing resonance. Now we shall calculate the amplitude and period of vibration in the variable
for discussing resonance. Now we shall calculate the amplitude and period of vibration in the variable![]() .
.
We may write the Equation (39) as
![]() (40)
(40)
where,
![]()
The solution of the equation
![]() (41)
(41)
is periodic and given by
![]() . (42)
. (42)
Let ![]() be the function of two independent variable
be the function of two independent variable ![]() i.e.
i.e.![]() .
.
The Equation (41) may be written as
![]() . (43)
. (43)
Then
![]() (44)
(44)
We want to replace ![]() from Equation (40) by two new variables
from Equation (40) by two new variables ![]() and
and ![]() which are related to
which are related to ![]() by Equation (42). As we are replacing one variable by other two co-relations between the new variables is at our choice. Let us choose it in such a way that
by Equation (42). As we are replacing one variable by other two co-relations between the new variables is at our choice. Let us choose it in such a way that
![]() . (45)
. (45)
Using Equations (44) and (45), we get ![]()
As ![]() are function of time
are function of time![]() , therefore differentiating it with respect to
, therefore differentiating it with respect to![]() , we get
, we get
![]() . (46)
. (46)
Using Equations (40), (43) and (46), we get
![]() . (47)
. (47)
Also from the Equation (46), we get
![]() . (48)
. (48)
Obviously the Equations (47) and (48) are linear equations in![]() .
.
So solving these equations for these variables, we get
![]() (49)
(49)
![]() (50)
(50)
where, ![]() is a function of
is a function of ![]() only.
only.
Also,
![]() . (51)
. (51)
As ![]() are function of
are function of ![]() only, we can write the Equation (51) into canonical form with new variables
only, we can write the Equation (51) into canonical form with new variables ![]() defined by
defined by
![]()
As ![]() so differentiating the Equation (50) and putting the value of
so differentiating the Equation (50) and putting the value of ![]() and
and![]() , we get
, we get
![]()
Neglecting higher powers of![]() , we get
, we get
![]() (52)
(52)
Here we observe that ![]() are present in
are present in ![]() only as the sum of the periodic terms with argument
only as the sum of the periodic terms with argument ![]() where
where ![]() are given constants, thus we have
are given constants, thus we have
![]()
The Equation (53) can be written
![]() . (53)
. (53)
Now we are considering here the case in which the critical argument is at the point ![]() then the affected Hamiltonian is given by
then the affected Hamiltonian is given by
![]() . (54)
. (54)
Taking ![]() as the critical argument in our case so the Equation (53) becomes
as the critical argument in our case so the Equation (53) becomes
![]() . (55)
. (55)
As the first approximation, if we put ![]() (All constants) then Equation (54) becomes
(All constants) then Equation (54) becomes
![]() . (56)
. (56)
This is the equation of motion of a simple pendulum. If co-efficient of ![]() is negative then
is negative then
![]()
If the oscillation is small, we can take ![]() as
as ![]() oscillates about the value of 0 or
oscillates about the value of 0 or![]() . Then Equation (56) becomes
. Then Equation (56) becomes
![]()
![]()
where ![]()
![]()
Its solution is given by
![]() (57)
(57)
where ![]() and
and ![]() are arbitrary constants. Thus amplitude and period of vibration
are arbitrary constants. Thus amplitude and period of vibration
are given by ![]() and
and ![]() respectively with similar approximation in the first relation
respectively with similar approximation in the first relation
of Equation (50) and using the Equations (54) and (57), we get.
![]()
where ![]() can be determined from the equation
can be determined from the equation ![]() as
as ![]() is known function.
is known function.
7. Equilibrium Points for the Body A in Terms of Eulerian Angles
Now we calculate the libration in the variables![]() .
.
Integrating the Equation (33) and ignoring secular terms, we get
![]()
where constants of integration are taken to be zero.
Putting the value of ![]() in Equation (32) and ignoring secular term, we get
in Equation (32) and ignoring secular term, we get
![]()
where ![]() etc. are constants.
etc. are constants.
And the perturbed solution for ![]() is given by
is given by
![]() (58)
(58)
Obviously in the case of one of the denominator becomes zero, the motion cannot be determined at that point, known as critical point and hence resonance arise at that point. In this case usual method fails to determine the motion, so for the present purpose the present purpose we will use the method as that of![]() .
.
The equation for ![]() can be written as
can be written as
![]()
![]()
On taking the first approximation, we can see that critical argument oscillates about
![]() or
or![]() . Also the solution for
. Also the solution for ![]() is given by
is given by
![]() (59)
(59)
where ![]() and
and ![]() are arbitrary constant.
are arbitrary constant.
Thus amplitude and period of vibration are given by ![]() and
and ![]() respectively, where
respectively, where![]() ,
,
![]()
![]()
The solution for ![]() is given by
is given by
![]() (60)
(60)
where ![]() can be determined from the equation
can be determined from the equation ![]() as
as ![]() is a known function. From the Equation (34) it is obvious that
is a known function. From the Equation (34) it is obvious that ![]() depends on
depends on ![]() so that all the results of
so that all the results of ![]() can be found in terms of
can be found in terms of![]() .
.
8. Equilibrium Points for the Body B in Terms of Eulerian Angles
By proceeding exactly same as above case, we can find out the libration in the variables![]() . Here, we assume that
. Here, we assume that ![]() is a small quantity and at the equilibrium point
is a small quantity and at the equilibrium point ![]() i.e. mean motion and angular velocity of the body B are in the ratio of 1:2. Therefore at this point the resonance will arise. By taking
i.e. mean motion and angular velocity of the body B are in the ratio of 1:2. Therefore at this point the resonance will arise. By taking
![]()
and the solution up to first order approximation of![]() , we get
, we get
![]() (61)
(61)
![]() (62)
(62)
![]() are arbitrary constants.
are arbitrary constants.
![]() . (63)
. (63)
Also we see that in the libration in the variable ![]() the critical argument variable
the critical argument variable ![]()
makes oscillation about the value ![]() and the period of libration is given by
and the period of libration is given by![]() .
.
The solution of ![]() for small oscillation is given by
for small oscillation is given by![]() , where
, where ![]() and
and ![]() are arbitrary constant.
are arbitrary constant.
![]()
![]() is a function of
is a function of ![]() only.
only.
![]()
Solution for ![]() is given by
is given by
![]()
Also when we consider the libration in the variable ![]() we see that the critical
we see that the critical
argument ![]() will make oscillation about the value
will make oscillation about the value ![]() and the period of libration is given by
and the period of libration is given by![]() .
.
The solution of ![]() for small oscillation in this case will be
for small oscillation in this case will be![]() , where
, where ![]() and
and ![]() are arbitrary constant.
are arbitrary constant.
![]()
![]()
![]()
And the solution for ![]() is given by
is given by
![]() . (64)
. (64)
where ![]() can be determined from the equation
can be determined from the equation ![]() as
as ![]() is a known function.
is a known function.
From the Equation (37) it is obvious and ![]() depends on
depends on![]() , so that the result of
, so that the result of ![]() can be found in term of
can be found in term of![]() .
.
9. The Solution for the Generalized Momenta Variables Corresponding to Constants of Integration
We have from Equation (16),
![]()
Integrating the Equation (17) with respect to![]() , we get
, we get
![]()
![]()
Initially at ![]() take
take ![]() and using the Equation (16), we get
and using the Equation (16), we get
![]()
where,![]() .
.
Again from Equation (18), we have
![]()
Initially at ![]() take
take ![]() and using the Equation (14), we get
and using the Equation (14), we get
![]()
where,![]() .
.
Now we find the time ![]() that elapses between the instant at which
that elapses between the instant at which ![]() attains successive minima and
attains successive minima and ![]() the corresponding change in
the corresponding change in![]() .
.
We have![]() . Clearly
. Clearly ![]() attains it successive minima at
attains it successive minima at![]() .
.
Let ![]() when
when ![]() when
when![]() . Then from Equations (14) and (34), we have
. Then from Equations (14) and (34), we have
![]()
Again from the Equations (13) and (36), we get
![]()
Let ![]() when
when ![]() and
and ![]() when
when ![]()
The corresponding change in ![]() is given by
is given by ![]()
10. Conclusions
In the section of “Equations of motion”, we have derived the perturbed and unperturbed Hamiltonian and the canonical equations of motion with respect to the complete Hamiltonian H where are generalized co-ordinates and are the corresponding generalized momenta. In Section 3, unperturbed solutions can be derived by usual course from the Kepler’s equation of motion. For appropriate variational equation, the required generalized co-ordinates have been calculated in Section 5. In section 6, the effect of resonance has been shown in the solutions of the equations of motion of two cylindrical rigid bodies. In Section 7 and 8, equilibrium points have been calculated in terms of Eulerian angles for both the bodies.. Finally the appropriate variational equation in Section 4 has been completely solved in Section 9.
The tools obtained in different sections of the manuscript can be used to discuss the motion of cable connected two artificial satellites. Thus, we may conclude that this article is highly applicable in Astrophysics and Space Science.