1. Introduction
An analysis of the Reissner-Nordstrom metric shows that a spherically symmetric distri- bution of charged dust may avoid the catastrophic gravitational collapse, a seemingly unavoidable feature of Schwarzschild’s [1] geometry exterior to an electrically neutral fluid sphere of mass bigger than certain critical limit. As in evidence we have Bonnor’s model [2] [3] of the equilibrium ball of charged dust in contrast to the Oppenheimer- Snyder [4] continually contracting ball of electrically neutral dust. Though Bonnors model has been found to the unstable to small radial perturbations and also to a change in the total charge content of the system, it initiates a general interest in the study of the implications of Einstein-Maxwell field equations with reference to the general relativistic prediction of gravitational collapse. On the other hand, it is generally considered that a black hole may carry non-zero net charge, apart from its mass and angular momentum. Such an assumption may require the collapse of stellar masses of charged matter. It has been suggested by Shvartsman [5] that on account of interaction between a star and its surroundings, it is possible that stellar systems carrying electric charge may exist in nature. It is therefore not surprising that in recent years the problem of finding non- singular, physically meaningful solution of Einstein-Maxwell field equations for static ball of charged coherent perfect has received wide attention. The inclusion of charge seems to affect the stability of the system―the stability of Schwarzschild’s uniform density sphere increases by the introduction of net surface charge. It has been shown that the stability is more profound if the same amount of charge be distributed unifor- mally throughout within the sphere.
The search for the exact solutions is of continuous interest to researcher. Buchdahl [6] proposed a famous bound on the mass radius ratio of relativistic fluid spheres which is an important contribution in order to study the stability of the fluid spheres. Delgaty- Lake [7] studied all the then existing solutions and established that Adler [8] , Heintzmann [9] , etc. do not satisfy all the well behaved conditions and also pointed out that only nine solutions are well behaved; out of which seven in curvature coordinates (Tolman [10] , Finch and Skea [11] , Patvardhav and Vaidya [12] , Mehra [13] , Kuchowicz [14] , Matese and Whitman [15] , Durgapal’s two solutions [16] ) and only two solutions (Nariai [17] , Goldman [18] ) in isotropic coordinates. Ivanov [19] [20] [21] [22] [23] , Neeraj Pant [24] , Maurya and Gupta [25] , Pant et al. [26] [27] , Pant and Sah [28] [29] , Tewari, Charan and Chandra [30] , Sah, Chandra and Charan [31] studied the existing well behaved solutions of Einstein’s field equations. Some pioneer work in Relativity is given by Herrera et al. [32] - [37] , Tewari and Charan [38] [39] [40] [41] . Nduka [42] [43] , Whitman and Burch [44] , Tikekar [45] , Ivanov [46] , Ray et al. [47] , Stettner [48] , Krori and Barua [49] , Ray and Das [50] , Pant and Negi [51] , Florides [52] , Dionysiou [53] , Pant et al. [54] etc. gave the well behaved solution for charged fluid sphere. Pant et al. [55] , Pant and Tewari [56] , Fuloria et al. [57] gave charge analogue of Heintzmann, Adler, Durgapal’s relativistic exact solution respectively. Gupta and Maurya [58] gave charge analogue of Durgapal and Fuloria superdense star. Bijalwan and Gupta [59] , Gupta and Kumar [60] gave charge analogue of Schwarzschild’s interior solution.
In this paper, we present a new solution of Einstein-Maxwell field equations in sphe- rically symmetric coordinates which are well behaved solutions charge analogous solution of Sah and Chandra [61] . In our present study the paper consists of nine sections. In Section 2, Einstein’s field equations for charged fluid sphere in canonical coordinates are given. In Section 3, gravitational binding energy of a charged fluid sphere is given. Section 4 consists of boundary conditions for well behaved solutions. New class of solution of Einstein’s field equations for a charged fluid sphere in canonical coordinates is given in Section 5. Section 6 stipulates the properties of this new class of solution of Einstein-Maxwell field equations. In Section 7 the matching conditions of interior metric of the charged fluid with the exterior metric are given. For better illustration of our physically accepted solution, the relevant physical quantities are presented by tables and figures in Section 8. Finally, some concluding remarks have been made in Section 9.
2. Field Equations for a Charged Fluid Sphere in Canonical Coordinates
The Einstein-Maxwell field equations in general relativity are given by
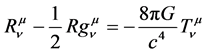 (1)
(1)
where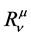 ,
, 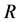 ,
, 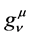 and
and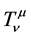 , are Ricci mixed tensor, scalar curvature, metric tensor and the energy momentum tensor for fluid sphere respectively.
, are Ricci mixed tensor, scalar curvature, metric tensor and the energy momentum tensor for fluid sphere respectively. 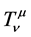 is conserved quantity such that
is conserved quantity such that
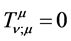 (2)
(2)
The energy momentum tensor for a charged fluid sphere is defined as
 (3)
(3)
Here  is the part of the energy momentum tensor due to matter distribution of the system and, for a perfect fluid distribution, it is given by
is the part of the energy momentum tensor due to matter distribution of the system and, for a perfect fluid distribution, it is given by
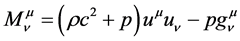 (4)
(4)
where  and
and 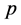 are the density and isotropic pressure of the fluid element measured locally in its proper reference frame. The density
are the density and isotropic pressure of the fluid element measured locally in its proper reference frame. The density 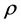 gives total matter energy in proper volume V as
gives total matter energy in proper volume V as
 (5)
(5)
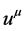 is element’s time-like four-velocity vector such that
is element’s time-like four-velocity vector such that
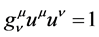 (6)
(6)
![]() is the part of energy momentum tensor due to electromagnetic character of matter within the fluid sphere and is defined by
is the part of energy momentum tensor due to electromagnetic character of matter within the fluid sphere and is defined by
![]() (7)
(7)
where the electromagnetic tensor ![]() satisfies Mexwells equations
satisfies Mexwells equations
![]() (8)
(8)
![]() (9)
(9)
![]() is the 4-current density for a fluid of null charge conductivity and a conserved quantity such that
is the 4-current density for a fluid of null charge conductivity and a conserved quantity such that
![]() (10)
(10)
and is given by
![]() (11)
(11)
![]() being the charge density of the fluid element and gives the total charge contained in proper volume V as
being the charge density of the fluid element and gives the total charge contained in proper volume V as
![]() (12)
(12)
The total non gravitational energy in a proper volume V is given by
![]() (13)
(13)
We consider a static spherically symmetric charged perfect fluid distribution. The interior space-time metric for spherically symmetric fluid distribution in canonical coordi- nate is given by
![]() (14)
(14)
where ![]() and
and ![]() are functions of r only.
are functions of r only.
The electrostatic field is described by the only non-singular components![]() ,
,
![]() of
of![]() .
.
In view of (8), (9) and (10) we obtain
![]() (15)
(15)
where Q stands for the total charge contained within the sphere of radius r and is given as
![]() (16)
(16)
In view of the metric (14) and energy momentum tensor (3), the field Equation (1) gives
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
In view of Equation (17) and Equation (18), pressure isotropy gives
![]() (20)
(20)
The charge conservation Equation (10) is identically satisfied whereas (2) for energy- momentum gives rise to the following surviving equation
![]() (21)
(21)
which is clearly contained in the field Equations (17) to (20).
We have three equations to determine five unknown functions![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . Thus, we find a two degree of arbitrariness in the general relativistic problem of the electrically charged fluid ball, and to obtain a solution we can always choose one of these functions arbitrarily and correlate other to this by certain relation. The volume field surrounding the charged sphere is described by the Reissner-Nordstrom field
. Thus, we find a two degree of arbitrariness in the general relativistic problem of the electrically charged fluid ball, and to obtain a solution we can always choose one of these functions arbitrarily and correlate other to this by certain relation. The volume field surrounding the charged sphere is described by the Reissner-Nordstrom field
![]() (22)
(22)
![]() (23)
(23)
where M and E are constants. We observe that whereas in Schwarzschilds field that total energy ![]() is constant, in case of Reissner-Nordstrom field the total energy
is constant, in case of Reissner-Nordstrom field the total energy
![]() increases as r increases. At large distances the Reissner-Nordstron field
increases as r increases. At large distances the Reissner-Nordstron field
approximates to Schwarzschilds field. The junction of interior and exterior field over the boundary ![]() of the sphere is governed by the junction conditions due to Darmois (1927), Viz. the continuity of the first and second fundamental forms across the boundary, which imply the continuity of
of the sphere is governed by the junction conditions due to Darmois (1927), Viz. the continuity of the first and second fundamental forms across the boundary, which imply the continuity of ![]() and the fluid pressure across the boundary. For the junction of electromagnetic field it is sufficient to consider the continuity of
and the fluid pressure across the boundary. For the junction of electromagnetic field it is sufficient to consider the continuity of ![]() (and not its first derivatives) across the boundary. In view of (16) and (23) the continuity of
(and not its first derivatives) across the boundary. In view of (16) and (23) the continuity of ![]() gives
gives
![]()
Thus the constant ![]() measures the total charge contained within the ball.
measures the total charge contained within the ball.
Also we have
![]() (24)
(24)
where
![]() (25)
(25)
and
![]() (26)
(26)
The continuity of ![]() over the boundary
over the boundary ![]() demands
demands
![]() (27)
(27)
Thus, in general, the constant M can not be identified with Euclidean mass of the sphere as against the case of uncharged sphere in which case![]() . In view of (27) we have
. In view of (27) we have ![]() we observe what the distribution of total energy within the charged sphere as measured by an electrically neutral test particle close to the boundary of the star is similar to that within a sphere of electrically neutral perfect fluid. Equation (27) can be rewritten as,
we observe what the distribution of total energy within the charged sphere as measured by an electrically neutral test particle close to the boundary of the star is similar to that within a sphere of electrically neutral perfect fluid. Equation (27) can be rewritten as,
![]() (28)
(28)
Thus three physical quantities contribute to ![]() viz. 1) the total matter energy within the ball distributed as if the geometry is Euclidean, 2) the total electromagnetic energy within the ball as if the geometry is Euclidean 3) the total electromagnetic energy distributed over the entire exterior space-time as if the geometry there too is euclidean.
viz. 1) the total matter energy within the ball distributed as if the geometry is Euclidean, 2) the total electromagnetic energy within the ball as if the geometry is Euclidean 3) the total electromagnetic energy distributed over the entire exterior space-time as if the geometry there too is euclidean.
The gravitational redshift of massive spherically symmetric ball is
![]() (29)
(29)
which gives central ![]() and surface
and surface ![]() gravitational redshifts
gravitational redshifts
![]() (30)
(30)
and
![]() (31)
(31)
3. Gravational Binding Energy of a Charged Sphere
In view of (11) the total non gravitational energy of a charged sphere is given
![]() (32)
(32)
Also the total energy of the ball measured by an electrically neutral test particle close to the boundary is given by
![]() (33)
(33)
Clearly the difference ![]() is the expression for the gravitational energy of the charged fluid sphere as measured by an observer close to the boundary. The negative of this quantity is the gravitational binding energy of the system. In Newtonian limit we obtain from (24), (32) and (33)
is the expression for the gravitational energy of the charged fluid sphere as measured by an observer close to the boundary. The negative of this quantity is the gravitational binding energy of the system. In Newtonian limit we obtain from (24), (32) and (33)
![]() (34)
(34)
For a particle at large distances from the object total energy ![]() approximates to
approximates to
![]() . The difference
. The difference ![]() between the two energy measurements is the classical
between the two energy measurements is the classical
expression for the energy of vacuum electrostatic field surrounding a sphere of charge ![]() and radius
and radius![]() . In the Reissner-Nordstrom field energy is distributed in the entire space time. As such the set of field Equations (17) to (19) can be solved under two given relations or assumptions. Physically speaking, one of them has to be the equation of state for fluid and another a law for the distribution of charge with the sphere. The non-singular solution due to Naduka [42] [43] and that due to Whitman and Burch [44] follow the charge distribution given by
. In the Reissner-Nordstrom field energy is distributed in the entire space time. As such the set of field Equations (17) to (19) can be solved under two given relations or assumptions. Physically speaking, one of them has to be the equation of state for fluid and another a law for the distribution of charge with the sphere. The non-singular solution due to Naduka [42] [43] and that due to Whitman and Burch [44] follow the charge distribution given by ![]() = constant.
= constant.![]() .
.
4. Boundary Conditions for Well Behaved Solution
For well behaved nature of the solution in isotropic coordinates, the following conditions should be satisfied:
1) The solution should be free from geometrical and physical singularities. Metric potentials A and B must be non-zero positive finite for free from geometrical singularities while central pressure, central density, should be positive and finite or ![]() and
and ![]() for free from physical singularities.
for free from physical singularities.
2) The solution should have maximum positive values of pressure and density at the center and monotonically decreasing towards the surface of fluid object i.e.
i) ![]() and
and ![]() such that the pressure gradient,
such that the pressure gradient, ![]() is negative for
is negative for
![]() .
.
ii) ![]() and
and ![]() such that the density gradient,
such that the density gradient, ![]() is negative for
is negative for
![]() .
.
3) At boundary pressure, ![]() must vanish.
must vanish.
4) The pressure, ![]() , and density
, and density ![]() should be positive.
should be positive.
5) Solution should have positive value of pressure-density ratio which must be less
than 1 (weak energy condition) and less than ![]() (strong energy condition) throughout
(strong energy condition) throughout
within the fluid object and monotonically decreasing as well (Pant and Negi [51] ).
6) The casualty condition must be satisfied for this velocity of sound should be less
than that of light throughout the model i.e.![]() . The velocity of sound should
. The velocity of sound should
be monotonically decreasing towards the surface and increasing with the increase of
density i.e. ![]() or
or![]() . In this context it is worth mentioning that
. In this context it is worth mentioning that
the equation of state at ultra-high distribution has the property that the sound speed is decreasing outwards.
7) For realistic matter, the adiabatic index ![]() i.e.
i.e.![]() , everywhere within the
, everywhere within the
ball.
8) The red shift at the center ![]() and at the boundary should be positive, finite and monotonically decreasing in nature with the increase of r.
and at the boundary should be positive, finite and monotonically decreasing in nature with the increase of r.
Under these conditions, we have to assume the one of the gravitational potential component in such a way that the field Equation (1) can be integrated and solution should be well behaved.
5. New Class of Well Behaved Solution
We present the following general analytic solution of the field Equations (17) to (20).
![]() (35)
(35)
![]() (36)
(36)
The isotropic pressures, matter-energy density, charge, charge density and red shift of charged fluid ball are given by
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
Here a, b, and d are arbitrary constants.
In order to construct a new relativistic model, we assume ![]() then we have
then we have
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
![]() (47)
(47)
![]() (48)
(48)
Here a, b, and d are arbitrary constants.
The variation in pressure, density, charge, charge density and red shift with radial distance are given as
![]() (49)
(49)
![]() (50)
(50)
![]() (51)
(51)
![]() (52)
(52)
6. Properties of the Solution
For real values of metric potentials A and B,![]() . Figure 1 shows that the metric potentials
. Figure 1 shows that the metric potentials ![]() and
and ![]() are positive at the center which are slightly and monotonically increasing with r for suitable choice of constants
are positive at the center which are slightly and monotonically increasing with r for suitable choice of constants![]() , and
, and![]() . For the positive central value of
. For the positive central value of![]() ,
,
The central value of![]() ,
, ![]() and
and ![]() are given as,
are given as,
![]() (53)
(53)
![]() (54)
(54)
![]()
Figure 1. Variation of metric potentials with![]() .
.
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
It is clear from Equation (53) to Equation (57) that for positive central values of physical quantities![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are positive if
are positive if![]() ,
, ![]() and
and
![]() . In view of Equations (49) and (50), the variation in the pressure and density
. In view of Equations (49) and (50), the variation in the pressure and density
with the distance from the center of fluid ball are identically zero at the center.
At the center of fluid ball the second order derivatives of pressure and density with respect to radial distance from the center of fluid ball are
![]() (58)
(58)
The pressure is maximum at the center if ![]() i.e.
i.e.![]() .
.
![]() (59)
(59)
The density is maximum at the center for all constants as![]() .
.
The central equation of state
![]() (60)
(60)
![]() must satisfies the condition
must satisfies the condition ![]() which demands
which demands ![]() and
and![]() .
.
The central value of ![]() is given by
is given by
![]() (61)
(61)
The causality condition at the center ![]() gives
gives
![]() .
.
It is found that ![]() and
and ![]() fall monotonically from their maximum positive values at the center up to non negative values at the boundary (Figure 2) and
fall monotonically from their maximum positive values at the center up to non negative values at the boundary (Figure 2) and ![]() falls mono- tonically from it’s maximum positive values at the center up to zero value at the boundary while charge increases from zero at the center to maximum positive value at the boundary (Figure 3) for different values of the parameters
falls mono- tonically from it’s maximum positive values at the center up to zero value at the boundary while charge increases from zero at the center to maximum positive value at the boundary (Figure 3) for different values of the parameters![]() ,
, ![]() ,
, ![]() satisfying
satisfying
![]() (62)
(62)
![]()
Figure 2. Variation of energy density, charge density and red shift with![]() .
.
![]()
Figure 3. Variation of pressure, pressure density ratio and charge with![]() .
.
Figure 4 shows that speed of sound is less than speed of light i.e. ![]() and the ratio of speeds of sound and light
and the ratio of speeds of sound and light ![]() falls monotonically from center to the
falls monotonically from center to the
boundary of the fluid ball.
7. Matching Conditions of Boundary
The solution so obtained are to be matched over the pressure free boundary of fluid sphere smoothly with the Reissner-Nordstrom metric:
![]() (63)
(63)
which requires the continuity of ![]() and
and ![]() across the boundary
across the boundary ![]() and
and
![]() ;
;![]() . Thus
. Thus
![]()
Figure 4. Variation of adiabatic velocity of sound with![]() .
.
![]() (64)
(64)
![]() (65)
(65)
![]() (66)
(66)
where![]() ;
;![]() , Schwarzchild parameter.
, Schwarzchild parameter.
8. Tables of Numerical Values of Physical Quantities and Their Graphs
In view of Equations (64) to (66) the values of![]() ,
, ![]() ,
, ![]() and
and ![]() are 0.701, −0.062c,
are 0.701, −0.062c,
0.0823c and −0.0753 respectively and the value of ![]() for
for ![]() and surface density
and surface density![]() . For better illustration of our physically accepted solu- tion, the relevant physical quantities are presented by means of Table 1, Table 2 and Figures 1-4 for these constants.
. For better illustration of our physically accepted solu- tion, the relevant physical quantities are presented by means of Table 1, Table 2 and Figures 1-4 for these constants.
In order to construct a super dense star model, we prescribe the surface density of the star as ![]() and the values of constants
and the values of constants![]() ,
, ![]() and
and ![]() can be evaluated for different values of
can be evaluated for different values of ![]() for describing the well behaved solutions. Thus a compact star model can be constructed by finding mass and radius corresponding to assumed surface density. The variation in the mass and radius with schwarzschild parameters for our model of compact star is tabulated in Table 3 and the variation of surface charge, Surface Density, Schwarzschild Parameter and
for describing the well behaved solutions. Thus a compact star model can be constructed by finding mass and radius corresponding to assumed surface density. The variation in the mass and radius with schwarzschild parameters for our model of compact star is tabulated in Table 3 and the variation of surface charge, Surface Density, Schwarzschild Parameter and ![]() with
with ![]() showing different models is shown in Figure 5.
showing different models is shown in Figure 5.
9. Conclusion
We have given a new solution for spherically symmetric isotropic charged fluid ball. It has been observed that the physical parameters pressure, density, adiabatic speed of sound and redshift are positive at the centre and within the limit of realistic state equation and monotonically decreasing and the causality condition is obeyed through- out the fluid ball. The charge and electric field intensity are zero at the center and monotonincally increasing towards the intervening surface. Thus, the solution is well behaved for all values of Schwarzschild parameter ![]() within the charged fluid ball. Our solution is useful to construct the models of compact star like Strange star family,
within the charged fluid ball. Our solution is useful to construct the models of compact star like Strange star family,
![]()
Figure 5. Variation of surface charge, surface density, Schwarzschild parameter and ![]() with
with ![]() showing different models.
showing different models.
Neutron star and many more. We have discussed a model of massive neutron star having mass ![]() and radius 14.66 km with surface density
and radius 14.66 km with surface density ![]() and central density
and central density![]() . The central pressure of neutron star is
. The central pressure of neutron star is
![]() while the surface pressure of the star is zero. The electric field intensity at the center is zero and at the surface it comes
while the surface pressure of the star is zero. The electric field intensity at the center is zero and at the surface it comes![]() . Table 3 shows that we can construct different models for neutron star having mass lies between
. Table 3 shows that we can construct different models for neutron star having mass lies between ![]() and
and ![]() for different values of
for different values of ![]() ranging from 0.15 to 0.259. The solution reduces to Schwarzschild interior solution for n = −1/2 for electrically neutral fluid ball.
ranging from 0.15 to 0.259. The solution reduces to Schwarzschild interior solution for n = −1/2 for electrically neutral fluid ball.