1. Introduction
Why was differential calculus developed? The consideration of this problem inevitably relates to the concept of movement. The analysis of the motion of an object is a major problem in physics. However, we can only observe the position of the object at a point in time. Thus, we can only measure an average velocity for an interval of time between observations. When the position of an object is given as a function of time, the average velocity from time t to time t + Δt is represented by
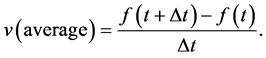 (1)
(1)
Formal differential calculus is based on the concept of the limit. As Δt decreases, the average velocity approaches the instantaneous velocity at time t. The instantaneous velocity at time t is denoted as v(t). Then, Equation (2) shows that the limit of v(average) is v(t) (Klein, 1998) :
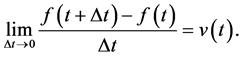 (2)
(2)
However, the average velocity never reaches the instantaneous velocity. Nevertheless, a limit of the average velocity is defined as the instantaneous velocity. This is difficult to accept intuitively.
Then, the novel method of differential calculus based on the double contradiction is introduced in this paper. The method is easier to accept intuitively than the traditional method of differential calculus. Furthermore, the meaning of the double contradiction in the foundation of mathematics is considered.
2. Zeno’s Arrow Paradox
When we try to determine the instantaneous velocity, we confront Zeno’s arrow paradox. Aristotle wrote (Aristotle, 1996) :
Zeno's reasoning is invalid. He claims that if it is always true that a thing is at rest when it is opposite to something equal to itself, and a moving object is always in the now, then a moving arrow is motionless. But this is false, because time is not composed of indivisible nows, and neither is any other magnitude.
Aristotle’s objection is legitimate. Surely, motion requires an interval of time. Since no time elapses at an instant, the arrow cannot move at an instant. Equation (3) shows that v(t) is indeterminate. That is, for Δt = 0,
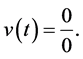 (3)
(3)
We must now consider how to determine instantaneous velocity. Usually, we can observe only the position of a moving object at a point in time. After we observe the positions of the object many times, we can postulate time-distance equation. We provide the following as an example of the differential calculus based on the double contradiction. If the motion of the object is the constantly accelerated motion with initial velocity 0 and acceleration a, the time-distance equation is
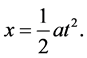 (4)
(4)
Next, when we apply the double contradiction to the constantly accelerated motion, we can determine the value of the indeterminate fraction in Equation (3). To apply the double contradiction, we need the average velocity after time t and before time t.
First, consider an arbitrary positive number h. Then, we calculate the average velocity from time t to time t + h. It is denoted as v(after), which is given in Equation (5):
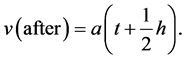 (5)
(5)
Second, consider a positive number g, which is smaller than t. We calculate the average velocity from time t-g to time t. It is denoted as v(before), which is given in Equation (6):
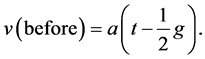 (6)
(6)
In this case, if we calculate an average velocity of the object in an interval many times, we can postulate that the velocity is monotonically increasing. Then, inequality (7) is established:
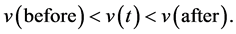 (7)
(7)
Substituting the definitions of v(before) and v(after), we obtain
 (8)
(8)
If v(t) is larger or smaller than at, both cases contradict inequality (8). This leads to Equation (9):
 (9)
(9)
Historically, Eudoxus developed the method of exhaustion for the quadrature of the curved figures (Klein, 1972; Heath, 1921) . Thus, the double contradiction was originally generated from geometry. The geometrical meaning of the differential calculus based on the double contradiction is important for its generalization.
3. The Geometrical Meaning of the Double Contradiction
We consider the geometrical meaning of the double contradiction. First, we confine the object of consideration to a smooth continuous curve. If a curve has convex and concave intervals, the curve between two proximate inflection points is either convex or concave. For simplification, we consider only the convex curve in the range of the positive real numbers. Similar logic can be applied to the concave curve.
Figure 1 shows the smooth continuous convex curve in the range of the positive real numbers. First, we draw chord AB. Second, consider point C, which is a point on arc AB. Obviously, point C is under chord AB. We then draw chord AC and chord CB.
Next, the slope of line AC plus (π − ∠ACB) equals the slope of line CB. Obviously, the slope of line CB is larger than that of line AC. We denote the slope of line AC ass(left) and the slope of line CB ass(right). Then, we obtain
![]()
Figure 1. The smooth convex curve y = f(x) and the chords AB, AC, and CB.
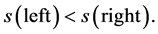 (10)
(10)
Next, point C is fixed. We focus on triangle ABC. As the length of AB decreases, ∠ACB approaches π without limit. However, ∠ACB never reaches π because point C must be under chord AB because the curve is convex. If we postulate that ∠ACB could be π, line AB would only touch the curve at point C. This line is the tangent at point C.
Although s(left) approaches s(right) without limit, s(left) cannot be equal to s(right). In this case, we can use the double contradiction. When we assume s(C) as the slope of the tangent at point C, inequality (11) is established:
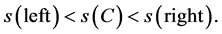 (11)
(11)
Then, the value of s(C) is determined by the double contradiction. First, we assume that the x-y coordinate of point C is (x, f(x)). Second, we assume that g is an arbitrary positive number less than x, and h is an arbitrary positive number. Then, the x-y coordinate of point A is 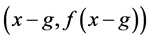 and the x-y coordinate of point B is
and the x-y coordinate of point B is 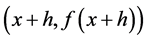 . Finally, the slope of the left-side chord and the slope of the right-side chord are represented by
. Finally, the slope of the left-side chord and the slope of the right-side chord are represented by
 (12)
(12)
The right sides of (12) are substituted into (11):
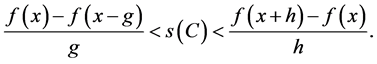 (13)
(13)
When the double contradiction is applied to inequality (13), s(C) can be only one value, which is the slope of the tangent. The slope of the tangent at point C is derived by the double contradiction.
Next, we consider the geometrical meaning of inequality (13). The line passing through point C can be placed into three categories. The first category corresponds to chord CB. Such lines cross the curve at point C and to the right of point C. The second category is the tangent, which only touches the curve at point C. The third category corresponds to chord AC. Such lines cross the curve at point C and to the left of point C.
Figure 2 shows the three categories of lines on the smooth continuous convex curve y = f(x). Line α represents those in the first category and line γ represents those in the third category. Line β is the tangent at point C. We denote the slope of line x ass(x), leading to the following Equations (14):
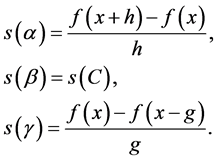 (14)
(14)
Substituting (14) into (13), inequality (15) is established:
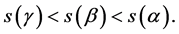 (15)
(15)
The geometrical meaning of inequality (15) is obvious. Only one line can be the tangent at point C. The slope of the tangent is determined by the double contradiction. The image is easy to accept intuitively. Furthermore, the differential calculus based on the double contradiction is founded on rigorous logic, as developed by Eudoxus.
![]()
Figure 2. Lines α, β, γ pass through point C on the smooth convex curve y = f(x).
4. Discussion
Initially, Zeno’s arrow paradox could be considered as a result of a feature of the human cognition of motion. Humans cannot distinguish between animation and real motion (Hoffman, 2000) . Hoffman described as follows.
When you watch a movie at the theater, what the projector shows you is a bunch of still pictures, one after the other. Each second, the projector shows you twenty-four different still pictures, and it rapidly flashes each of these pictures on and off three times, for a total of seventy-two flashes per second. In between flashes the screen is dark. Indeed, much of your time in the theater, while watching a movie, is spent before a blank screen.
When total 72 pictures are displayed on the screen in a second, we see a moving picture. That is, motion is created by our brain from still pictures. In other words, the motion which we cognize consists of the still images and the motion, the latter of which has been created by our brain. This is analogous to the mathematical description of motion described above, as it is created by our brain, but is not reality. Necessarily, we need to integrate the real and the model. The instantaneous velocity is determined by the double contradiction so that we maintain the compatibility between the model and the real.
Indeed, our brain’s model of motion requires instantaneous velocity. However, is instantaneous velocity required in real motion? Since time never stops, instantaneous velocity is not required in reality. Furthermore, what we regard as an instantaneous image is the creation of the brain. Even a high-speed camera needs an interval of time for the photography (High-speed camera, n.d.) and human eyes are far slower (Hubel, 1995). In fact, the instant itself may be a creation of the brain. If time does not stop, who can recognize an instant?
As discussed, our recognition of motion is deeply constrained by our brains. Hence, Zeno’s arrow paradox is a paradox in the model of motion created by our brains. Further, the solution of Zeno’s arrow paradox by double contradiction is only in our brain’s model of motion. Also, our mathematics may be prescribed by our brain. Thus, when we try to incorporate differential calculus based on the double contradiction into mathematics, we must consider the feature of the cognition of our brain.
Finally, we consider the meaning of the double contradiction in the foundation of mathematics. Knowledge of both mathematics and neuroscience is required for this. Stanislas Dehaene, a mathematician and neuroscientist, stated the following (Dehaene, 2011) :
As humans, we are born with multiple intuitions concerning numbers, sets, continuous quantities, iteration, logic, and the geometry of space. Mathematicians struggle to reformalize these intuitions and turn them into logically coherent systems of axioms, but there is no guarantee that this is at all possible. Indeed, the cerebral modules that underlie our intuitions have been independently shaped by evolution, which was more concerned with their efficiency in the real world than about their global coherence. This may be the reason why mathematicians differ in their choice of which intuitions to use as a foundation and which to relinquish.
Furthermore, Dehaene introduced Brouwer as the founder of constructivism. Brouwer rejected the application of the law of excluded middle to the infinite set. The law of excluded middle is the premise of reductio ad absurdum. Thus, if we aspire to constructive mathematics, we must be careful when accepting the result of reductio ad absurdum.
For example, when it is elucidated that the length of the diagonal line of the square is not the rational number by reductio ad absurdum, we have two options. One, we can reject the irrational number and conserve the constructive mathematics, which might appeal to the Ancient Greeks as they called the irrational number “the irrational magnitude” and excluded it from the set of numbers. Two, we can expand the realm of numbers without a regard to constructive mathematics, which is the option chosen by most modern mathematicians.
However, there is a gap between arithmetic and geometry, with the discovery of the irrational magnitude demonstrating incoherence between them. The Ancient Greeks struggled to fill the gap. Finally, Eudoxus developed the theory of proportion, which is in Euclid’s Elements (Euclid, 1956) . Definition 5 in book 5 of Elements corresponds exactly to the Dedekind cut (Dedekind, 1963) . We can define the irrational number using the rational numbers with a Dedekind cut. However, we cannot determine whether the irrational number exists. This problem remains.
The next problem is the quantification of the curved figure in the Euclidean plane. Euclid defined the straight line as “a breadthless length” in definition 2 of book 1 (Euclid, 1956) . When we accept this definition, we cannot define the curve. Further, since length is the length of the straight line, we cannot directly define the length of the curve. If a line is a breadthless length, the curve cannot be a line. In this situation, the existence of the curve itself is doubted. Still, the length of the curve can be approximated by line segments. Archimedes developed the method of the iteration of pi (Archimedes, 1897) .
Archimedes used inscribed and circumscribed regular polygons to approximate pi. As the number of sides increased, the ratio of perimeters to the diameter of the circle would converge to pi. This method allows us to approximate pi as precisely as desired, in principle. Thus, if Archimedes’ method of the iteration of pi is applied repeatedly without limit, lengths of line segments are divided into two groups: those longer than pi and those shorter than pi. Then, the value of pi can be defined by the double contradiction. This situation resembles the Dedekind cut, in which an irrational number divides rational numbers into two groups but the irrational number itself is not a rational number. In the same way, pi divides lengths of line segments into two groups, but pi itself is not a length of a line segment. Archimedes’ method serves both as the definition and the iteration of pi, but it does not ensure the existence of pi. Thus, Archimedes’ method of the iteration of pi is isomorphic to the Dedekind cut. Also, Archimedes iterated and defined areas of curved figures by rectilinear figures using the double contradiction, which is also isomorphic to the Dedekind cut.
Now, we recall the claim of Brouwer. Reductio ad absurdum must be excluded in constructive mathematics. Thus, when we use the double contradiction, we necessarily renounce the constructive mathematics. That is, there are two gaps in mathematics. The first gap is between arithmetic and geometry; the second gap is between geometry and calculus. Calculus was developed for handling the curve. It is difficult for us to handle the curve quantitatively in Euclidean geometry because Euclid did not define the length of the curve.
5. Conclusion
In conclusion, our mathematics is based on many intuitions, and the coherence of intuitions is not guaranteed. Thus, the existence of gaps in mathematics is a necessity. However, the Ancient Greeks tried to fill gaps in mathematics and developed the double contradiction in an attempt to maintain coherence in mathematics. It is time to once again pay attention to the double contradiction.