1. Introduction
In his seminal work of 1905 [1] and again in a later paper [2] in 1907 A, Einstein originated the idea that clocks actually measure a duration, which is proportionate to the length of their respective world-lines1; an assumption, which is known today as the clock-hypothesis. This hypothesis underlies much of the geometric structure of the theories of relativity [3] . The clocks in the original work are no further specified other than they are ideal, point-like devices. Much work has been done since then on the topic of relativistic clocks, either by experimentally confirming the hypothesis through detection of time-dilation in specific clock-devices [4] [5] [6] [7] , or by showing limitations of the hypothesis including critique on the before mentioned experiments [8] [9] [10] . Experiments have so far mainly been based on either moving particles, like muons, or on atomic clocks, i.e. atoms emitting/absorbing light without recoil, possible due to the Mössbauer-effect [11] . Some recent work focuses on the fact that real clocks are never point-like entities and that consequently forces between its constituent parts or between different clock-devices can influence the duration-measurement at the quantum level. The considerable machinery of quantum-field theory in curved space-time is applied in [9] to describe gravitational effects on the clocks or in [10] to find e.g. an impact of particle-creation on the duration measurement. Other recent work centers around the question, which clock-devices qualify as relativistic clocks and which ones do not [12] .
In this short note, we will use a simple model, using elementary tools only, to describe two classes of clocks: moving particle-based clocks, especially electrons, and atomic clocks. We will show that they are indeed relativistic clocks and will rediscover a hypothesis by L. de Broglie [13] , concerning internal clocks of electrons. At the same time, we will be able to understand some of the critical arguments mentioned above. Our aim is to give a precise, yet accessible account of the subject.
2. Relativistic Clocks
Let’s first consider a quantum system represented by a wave function  determined by the Schrödinger equation
determined by the Schrödinger equation
 (1)
(1)
By the time-energy inequality and a result in [14] , there holds for the minimal time T until  evolves into an orthogonal state
evolves into an orthogonal state ,
, 
 (2)
(2)
In (2)  and
and  represent the first and second moment of the energy operator H. Let us assume that the system
represent the first and second moment of the energy operator H. Let us assume that the system  is in its local rest-frame and ticks with frequency T2. By (2) it produces in an incremental time-step
is in its local rest-frame and ticks with frequency T2. By (2) it produces in an incremental time-step  the (incremental) number of flips (orthogonal states)
the (incremental) number of flips (orthogonal states) 
 (3)
(3)
To describe the first class of clocks based on (3) we think of the system 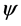 to be a particle with total (average) relativistic energy E and describe it in a semi-classical way. Then by (2) Equation (3) turns in the local rest frame into
to be a particle with total (average) relativistic energy E and describe it in a semi-classical way. Then by (2) Equation (3) turns in the local rest frame into
 (4)
(4)
The energy E represents kinetic and inner energy, defining the time-component of the four momentum  along the world-line
along the world-line  We can parametrise x by its write four-length s and (4) in covariant form by
We can parametrise x by its write four-length s and (4) in covariant form by
 (5)
(5)
The expression  denotes the four-scalar product. We will omit the subscript in the sequel. We can now write with
denotes the four-scalar product. We will omit the subscript in the sequel. We can now write with ![]() denoting the rest mass of the particle
denoting the rest mass of the particle
![]() (6)
(6)
There holds along any (time-like) world line
![]() (7)
(7)
For electrons, satisfying ![]() where
where ![]() denotes the Dirac four-momentum operator, Equation (7) holds indeed on the expectation-value level.
denotes the Dirac four-momentum operator, Equation (7) holds indeed on the expectation-value level.
Therefore, by integration, we get for any distance ![]() on the world line
on the world line
![]() (8)
(8)
Equation (8) confirms that electrons can indeed act as relativistic clocks, ticking with an internal frequency of a multiple of![]() . This is an idea, which was already suggested by L. de Broglie [13] . It is interesting to note that, if we chose the minimal time to pass through N orthogonal states, N large, instead of the minimal time to flip between two states, then we get
. This is an idea, which was already suggested by L. de Broglie [13] . It is interesting to note that, if we chose the minimal time to pass through N orthogonal states, N large, instead of the minimal time to flip between two states, then we get ![]() [14] and hence instead of (8)
[14] and hence instead of (8)
![]() (9)
(9)
a result, which fits well in the discussion in e.g. [15] .
![]()
3The expectation value is taken with respect to the state![]() .
.
Another class of clocks consists of atomic devices, where ![]() is the energy difference between two quantum levels
is the energy difference between two quantum levels ![]() and
and ![]() of a photon emitting/absorbing atom with Hamiltonian
of a photon emitting/absorbing atom with Hamiltonian![]() , which can be recoil-free due to the Mössbauer effect [11] 3. By (2) and (3) we get in the local rest-frame
, which can be recoil-free due to the Mössbauer effect [11] 3. By (2) and (3) we get in the local rest-frame
![]() (10)
(10)
The most direct ansatz for a covariant formulation of (10) is to simply chose the length s of the world-line of the clock as the parameter. We get
![]() (11)
(11)
If (11) is correct, then atomic clocks are indeed relativistic clocks as well. Let’s gather evidence for it and assume first that the clock (atom) is in transversal uniform motion relative to an observer at rest. We have
![]() (12)
(12)
Therefore, we get for the frequency ν in the frame of the observer
![]() (13)
(13)
where as usual![]() . This is the (transversal) Doppler-effect and its presence in atomic clocks has been observed in experiments [5] .
. This is the (transversal) Doppler-effect and its presence in atomic clocks has been observed in experiments [5] .
With ![]() denoting the oscillation-period, Equation (11) also leads to the expression for the time-dilation (red-shift) of a clock at rest in a static space-time, relative, for example, to an observer far away from the source of the gravitational field. With the line-element being
denoting the oscillation-period, Equation (11) also leads to the expression for the time-dilation (red-shift) of a clock at rest in a static space-time, relative, for example, to an observer far away from the source of the gravitational field. With the line-element being![]() , we have
, we have
![]() (14)
(14)
Hence
![]() (15)
(15)
The effect of gravitational red-shift on atomic clocks (15) has indeed been observed as well [6] . Expressions (13) and (14) and their empirical verification are evidence that (11) is correct.
3. Some Observations
Experiments with the two kinds of clocks support the clock-hypothesis and our elementary model gives an accessible theoretical framework to explain it. The basis was that we managed to establish a relation (3) between the internal evolution of a system and the length of the world line it is supposed to pass through. While, of course, we compromised in principle by choosing a semi-classical treatment, it seems that, compared to moving particles, atomic clocks are even less ideal devices though, since they are not point-like, and Equation (11) only holds neglecting any real clock components other than the photon-emission/absorption. There might be effects on the photon by other parts of the clocks [9] or a more sophisticated description of the oscillator by a quantum-field might lead to particle-creation [10] . Qualitatively, we can see already from our model, e.g. by (4) or (10), that particle-creation must lead to a time-dilation in the order of magnitude of the energy of the created particles, which is no longer available to process the clock.
It is not obvious to see how systems, which cannot be brought into a covariant form of type (3)
![]() (16)
(16)
could support the clock-hypothesis. Special relativity is the result of a conceptual merger of (classical) particle dynamics with electrodynamics. It is interesting to notice, that the clock-hypothesis is indeed best confirmed by devices, which are based on either of the two pillars: particle motion or electromagnetism. Systems, whose internal evolution base on other forces, like thermal energy, seem more resistant to confirm the hypothesis [12] .
More work will be done on the question of clocks in order to tackle the deeper issue, namely the one of the true nature of time.
NOTES
![]()
1The notionoffour dimensional worldline was introducedonlylater in 1908 by H. Minkowski.
![]()
2We need, of course, an assumption on size to justify a singel time-parameter t and hence (1).