1. Introduction
Li3AlP2 and Li3AlAs2 are filled tetrahedral NowotnyJuza compounds [1,2] with an orthorhombic structure and belong to the space group Ibca (73) [3] in contrast to cubic nitride semiconductors such as Li3AlN2 and Li3GaN2 [1,3]. Crystal structure of Li3AlP2 depicted by Juza et al. [3] and has been grown by direct reaction of Li, Al, and P in an evacuated quartz ampoule [4]. A filled tetrahedral compound (such as Li3AlP2) can be viewed as zincblend-like (Li0.5Al0.5P)– lattice filled with He-like Li+ ions at the empty tetrahedral sites. The available experimental studies on Li3AlP2 are limited to growth and optical band gap [4]. Kuriyama et al. have grown Li3AlP2 by direct reaction between Li, Al and P using photoacoustic spectroscopy method and obtained a band gap of 2.75 eV. (Unfortunately we do not have any experimental or theoretical information about Li3AlAs2). From theoretical point of view, to our knowledge, there is no theoretical research on electronic and structural properties. Moreover, it seems that there is a lack of both experimental and theoretical data on electronic and structural properties of Li3AlP2 and Li3AlAs2. In this work, we present the results of a systematic study of the electronic and structural properties of Li3AlP2 and Li3AlAs2 obtained by full potential linearized augmented plane wave (FP-LAPW) method with the generalized gradient approximation (GGA) for the exchange correlation potential, within the density functional theory. This work is along the latest study that is peformed on Li3AlN2 and Li3GaN2 about the electronic and optical properties of these compounds [5]. Our calculated results could serve as a reference for future theoretical and experimental works on these compound. The rest of this paper organized as follows. A brief description of our calculation method is given in Section 2. Section 3 contains the results and the conclusions are given in Section 4.
2. Calculation Method
The calculations presented in this work were performed using the full potential linearized augmented plan wave (FP-LAPW) method. In this method no shape approximation on the potential or on the electronic charge density is made. The calculations of the electronic and structural properties have been done relativistically. We use the WIEN2K [6] implementation of the method which allows the inclusion of local orbitals in the basis, improving upon linearization and making possible a consistent treatment of the semicore and valence states in an energy window, hence ensuring proper orthogonality. The exchange correlation potential within the generalized gradient approximation (GGA) is calculated using the scheme of Perdew et al. [7]. The convergence parameter , (the product of the smallest of the atomic sphere radii
, (the product of the smallest of the atomic sphere radii  and the plane wave cutoff parameter
and the plane wave cutoff parameter ) which controls the size of the basis sets in these calculations, was set to 8. The maximum
) which controls the size of the basis sets in these calculations, was set to 8. The maximum  quantum number for the wave function expansion inside the atomic sphere is confined to
quantum number for the wave function expansion inside the atomic sphere is confined to  = 10. The
= 10. The  parameter was taken to be 12.0 Bohr–1. Brillouin-zone (BZ) integrations within the self-consistency cycles were performed via a tetrahedron method [8], using 170 K points in the irreducible BZ. For the calculation of the density of states (DOS) however, a denser sampling of the BZ was needed, where we used 427 K points. The muffintin radii of Lithium (Li), Aluminium (Al) Phosphor (P) and Arsenide (As) were chosen as
parameter was taken to be 12.0 Bohr–1. Brillouin-zone (BZ) integrations within the self-consistency cycles were performed via a tetrahedron method [8], using 170 K points in the irreducible BZ. For the calculation of the density of states (DOS) however, a denser sampling of the BZ was needed, where we used 427 K points. The muffintin radii of Lithium (Li), Aluminium (Al) Phosphor (P) and Arsenide (As) were chosen as  = (2.32, 2.16, 2.16) a.u. for Li3AlP2 and (2.41, 2.26, 2.26) for Li3AlAs2. All these values have been chosen in a way to ensure the convergence of the results.
= (2.32, 2.16, 2.16) a.u. for Li3AlP2 and (2.41, 2.26, 2.26) for Li3AlAs2. All these values have been chosen in a way to ensure the convergence of the results.
3. Results and Discussions
In this section, we express the structural and electronic properties of Li3AlP2 and Li3AlAs2. The results of studing electronic and structural properties are in Sections 3.1 and 3.2 respectively.
3.1. Total Energy Calculations
The orthorhombic phase of Li3AlP2 and Li3AlAs2 has 96 atoms, 48 Li, 16 Al and 32 P (As), per primitive cell. A Point worth to mention is that the similar phosphors (Arsenides) in the cell are not equivalent. The Wyckoff position [3] of Li, Al, and P1 (As1), P2 (As2), P3 (As3) and P4 (As4) atoms are as follows:
Li: 16f (x1, y1, z1) Al: 16f (x2, y2, z2)
P1 (As): 8a (0, 0, 0) P2 (As): 8c (u, 0, 0.25)
P3 (As): 8d (0.25, v, 0) P4 (As): 8e (0, 0.25, w)
The structure of Li3AlP2 (Li3AlAs2) is characterized by three Lattice parameters a, b and c, and the internal parameters of atoms.
In our Literature survey, we did not find any theoretical works on calculating the lattice parameters and internal parameters for these compounds and nor any theoretical work on electronic and structural properties of them. Therefore to our knowledge, this part of the work can be considered as the first ab initio calculation for these compounds.
Experimental information about these compounds involves the positions of Al and P(As) and there is no information about the position of Li, In this work we first optimized the internal parameters by relaxing the atomic positions inside a unit cell using experimental lattice parameters [3]; the force on each atom after relaxation decreased to less than 0.5 mryd/a.u. We then used the optimized internal parameters to calculate the total energy of primitive unit cell as a function of their volume and fitted the results with Murnaghan equation of state [9] (Figure 1).
Our optimized internal parameters and lattice parameters are compared with experimental results in Tables 1 and 2.
It is evident from this data that our results agree rather well with experimental work. By calculating the total energy at different volumes and fitting the results with

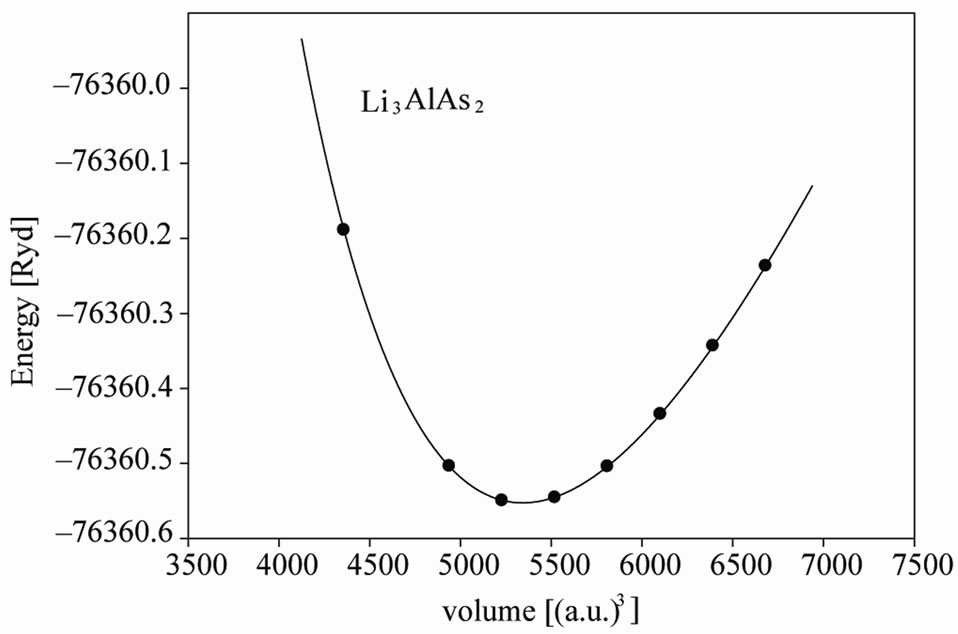
Figure 1. Total energy versus primitive unit cell volume of Li3AlP2 and Li3AlAs2.

Table 1. Lattice parameters, atomic position, bulk modulus (B) and its pressure derivative (B) of Li3AlP2. Experimental results are included for comparison.

Table 2. Lattice parameters, atomic position, bulk modulus (B) and its pressure derivative (B) of Li3AlAs2. Experimental results are included for comparison.
Murnaghan equation of state. We obtained the equilibrium lattice constants, bulk modulus and their pressure derivative. We show the energy—volume curve for Li3AlP2 and Li3AlAs2 structure in Figure 1 and compare the results with available experimental results in Tables 1 and 2.
3.2. Electronic Structure
Our calculated density of states (DOS) and electronic band structure for Li3AlP2 and Li3AlAs2 are given in Figures 2 and 3. Due to the close similarity between the results obtained for these compounds, the Partial Dos are given only for Li3AlP2. Major contribution to occupied part of the DOS come from the P (As) 3s (4s) and 3p (4p) states along with Al 3s and 3p states.
The first structure in the low lying energy side of the DOS consists of a peak centered on –10 (–11) eV for Li3AlP2 (Li3AlAs2) and originates from P (As) s states and Al s and p states, corresponding to the lowest lying bands in Figure 3.
The next structure which is separated from the first by a gap of 2.53 eV (3.28) for Li3AlP2 (Li3AlAs2) is a broad


Figure 2. Total DOS for two compounds (left) and partial density of states for Li3AlP2 (right).
peak that is situated between –6.7 (–7.0) eV and the Fermi level, corresponding, to the valence bands shown in the band structure in Figure 3. From the partial DOS, it is seen that just below the Fermi level, the bands are dominated by the P (As) p states and Al p states.
There is a main feature in the broad structure above the Fermi level up to 20 eV, containing a broad peak


Figure 3. Energy band structure of Li3AlP2 (left) and Li3AlAs2 (right).
from p and s states of Aluminium (below 5 eV) and p and s states of Lithium (above 5 eV).
In Li3AlP2 we found an indirect band gap between the top of phosphor valence P bands maximum occurring at the H point and the bottom of the Al s bands occurring at the Γ point. The difference between the calculated indirect band gap and the direct band gap at the center of BZ is too small. The indirect band gap value is 2.36 eV while the direct is 2.38 eV. The calculated values of the band gap for Li3AlP2 confirms the well known expectation that the theoretical band gaps are on the whole underestimated within GGA, in comparison with experimental value (2.75 eV) [4]. In Li3AlAs2 we found a direct band gap (1.49 eV) at the BZ center. Unfortunately we do not have any experimental information for comparison.
4. Conclusions
We have applied FP-LAPW method to study the electronic and structural properties of the filled tetrahedral semiconductors Li3AlP2 and Li3AlAs2 within density functional theory. During this study the positions of Li, Al, and P (As) have been obtained for the first time. Using these positions the structural parameters such as equilibrium lattice constants, bulk modulus and their pressure derivative have been calculated. The electronic properties such as total and partial electronic DOS and band structure have been calculated. The study of density of states indicated the main contribution of DOS consists of P (As) 3p (4p) and P (As) 3s (4s) states. The nature of the fundamental gap in Li3AlAs2 was found to be direct. According to our results, Li3AlP2 could be considered a material with a direct gap, because the difference between the direct (2.38 eV) and indirect (2.36 eV between H and Γ points) gap is very small. The calculated value of the band gap is in good agreement with experimental value (2.75 eV). Unfortunately in Li3AlAs2 we do not have any experimental result for comparison.