Adaptive Finite Element Method for Steady Convection-Diffusion Equation ()
Received 24 June 2016; accepted 27 September 2016; published 30 September 2016

1. Introduction
This paper deals with the scalar convection-diffusion equation. This equation describes the transport of scalar quantity, e.g., temperature or concentration. We are interested in the convection dominated case. In this case, the solution of a convection-diffusion equation frequently has boundary or interior layers. It is well known that the standard Galerkin finite element discretization on uniform grids produces inaccurate oscillatory solutions to convection diffusion problems. Therefore several stabilized finite element methods have been developed, e.g., the streamline-upwind Petrov-Galerkin (SUPG) method [1] & [2] or streamline-diffusion finite element method (SDFEM) [3] is designed to overcome these problems by introducing a small amount of artificial diffusion in the direction of streamlines. The numerical solution obtained from the SDFEM has the desirable property that the accuracy in regions where the exact solution is smooth will not be degraded as a result of discontinuities and layers in the exact solution [4] & [5] . However, the numerical solution obtained from the SDFEM can be oscillatory in regions where there are layers. One common technique to increase the accuracy of the finite element solution in these critical regions is through local grid refinement, the so-called h-method. The question is how to identify those regions and how to obtain a good balance between the refined and unrefined regions such that the overall accuracy is optimal.
Another related problem is to obtain reliable estimates of the accuracy of the computed numerical solution. A priori estimate are often insufficient and can’t be used to estimate the exact error. Therefore, it is natural to acquire a posteriori error estimators to pinpoint where the error is large and, at the same time, properly bound the exact error on the whole domain. The error estimator should be local and should yield reliable upper and lower bounds for the true error in a user-specified norm. Global upper bounds are sufficient to obtain a numerical solution with accuracy below a prescribed tolerance. Local lower bounds are necessary to ensure that the grid is correctly refined so that one obtains a numerical solution with a prescribed tolerance using a nearly minimal number of grid-points.
For two-dimensional problems, several estimators have been shown to be asymptotically exact when used on uniform meshes provided the solution of the problem is smooth enough [6] - [8] . Estimators based on computing residuals, so-called residual-type estimators, and estimators based on solving a local Dirichlet problem, so-called Dirichlet-type estimators, were introduced in [9] . Estimators based on solving a local Neumann problem, so- called Neumann-type estimators, were first given in [10] . These estimators have been studied by many researchers in [11] - [16] . The Zienkiewicz-Zhu (ZZ) type of estimators based on recovery of gradient and Hessian are also well developed, see [17] & [18] , and articles cited therein.
In this paper we introduce and analyze from theoretical and experimental points of view an adaptive scheme to efficiently solve the convection-diffusion equation. This scheme is based on the streamline-diffusion finite element method (SDFEM) introduced in [3] combined with an error estimator similar to the one developed in [14] . We prove global upper and local lower error estimates in the energy norm, with constants which only depend on the shape-regularity of the mesh and the polynomial degree of the finite element approximating space. We perform several numerical experiments to show the effectiveness of our approach to capture boundary and inner layers sharply and without significant oscillations.
The paper is organized as follows. In Section 2 we recall the convection-diffusion problem under consideration and the Streamline Diffusion Finite Element Method. In Section 3 we define a posteriori error estimator with the energy norm of the finite element approximation error. Finally, in Section 4, we introduce the adaptive scheme and report the results of the numerical tests.
2. Linear Convection-Diffusion Equation
We consider the following steady linear convection-diffusion equation
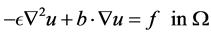 , (2.1a)
, (2.1a)
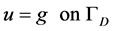 , and (2.1b)
, and (2.1b)
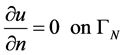 (2.1c)
(2.1c)
where 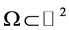 is a bounded polygonal domain with Lipschitz boundary
is a bounded polygonal domain with Lipschitz boundary 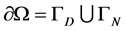 and
and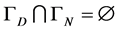 . We are interested in the convection dominated case and assume that
. We are interested in the convection dominated case and assume that
(A.1)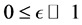 ,
,
(A.2)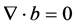 ,
,
(A.3) ,
,
(A.4)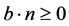 .
.
The 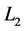 norm and the
norm and the 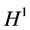 semi-norm (also called Energy Norm) are defined as
semi-norm (also called Energy Norm) are defined as
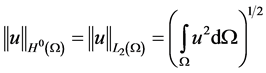 and (2.2)
and (2.2)
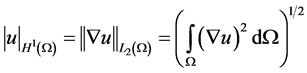 (2.3)
(2.3)
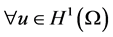 , respectively. We shall denote the above norm and semi-norm by the following convention
, respectively. We shall denote the above norm and semi-norm by the following convention
![]() and
and ![]() if no subscript index is given then we assume an ordinary
if no subscript index is given then we assume an ordinary ![]()
norm, ![]() , and if no subscript index is given then we shall assume it is the whole of
, and if no subscript index is given then we shall assume it is the whole of![]() .
.
To define weak form of Equation (2.1), we need two classes of functions: the trial functions ![]() and the test solutions
and the test solutions![]() :
:
![]() (2.4)
(2.4)
![]() (2.5)
(2.5)
The standard variational formulation of Equation (2.1) is given by: Find ![]() such that
such that
![]() (2.6)
(2.6)
where
![]() and (2.7)
and (2.7)
![]() (2.8)
(2.8)
Let ![]() be a decomposition of
be a decomposition of ![]() into triangles.
into triangles.
We need to make the following geometrical assumptions on the family of triangulations ![]()
1) Admissibility: whenever ![]() and
and ![]() belongs to
belongs to![]() ,
, ![]() is either empty, or reduced to a common vertex, or to a common edge
is either empty, or reduced to a common vertex, or to a common edge
1) ![]() = the diameter of K = the longest side of
= the diameter of K = the longest side of ![]()
3) ![]() = the supremum of the diameter of the balls inscribed in
= the supremum of the diameter of the balls inscribed in ![]()
4) Shape regularity: the ratio of ![]() to
to ![]() is uniformly bounded i.e.,
is uniformly bounded i.e.,
![]() (2.9)
(2.9)
which means for any ![]() and for any
and for any ![]() there exists a constant
there exists a constant ![]() such that
such that ![]() where
where ![]() denotes the smallest angle in any
denotes the smallest angle in any![]() .
.
We define the finite element spaces
![]() (2.10)
(2.10)
for triangular elements, where ![]() is the space of polynomials of degree not greater than 1 on K.
is the space of polynomials of degree not greater than 1 on K.
In the case of convection-dominated problem, the standard Galerkin approximation of Equation (2.6) may produce unphysical behavior, oscillation, if the mesh is too coarse in critical regions. To circumvent these difficulties, stability of the discretization has to be increased by introducing artificial diffusion along streamlines. The Streamline-Diffusion Finite Element Method (SDFEM) [1] - [3] stabilizes a convection-dominated problem by adding weighted residuals to the standard Galerkin finite element method for hyperbolic equations which combines good stability with high order accuracy, convergence results are available (see [19] ).
The SDFEM yields the following discrete problem obtained: Find ![]() such that
such that
![]() (2.11)
(2.11)
where
![]() and (2.12)
and (2.12)
![]() (2.13)
(2.13)
In Equation (2.11), a constant ![]() must be chosen for every element K. Let the mesh Peclet number be de-
must be chosen for every element K. Let the mesh Peclet number be de-
fined by, ![]() where
where ![]() denotes the norm in
denotes the norm in![]() . From the analysis of the SDFEM, the
. From the analysis of the SDFEM, the
following choice of ![]() are optimal; see [20] :
are optimal; see [20] :
![]() (2.14)
(2.14)
where ![]() is a measure of the element length in the direction of the convection flow b. For other parameter choice, see [21] - [24] .
is a measure of the element length in the direction of the convection flow b. For other parameter choice, see [21] - [24] .
3. A Posteriori Error Estimator
In this topic, we introduce the analysis of a Neumann-type error estimator proposed in [14] which is an extension of the work [25] . In their work, they modify the well-known Bank and Weiser estimator [10] and using the idea of Ainsworth & Oden in [26] , they solve a local (element) Poisson problem over a suitably chosen (higher order) approximation space with data from interior residuals and flux jumps along element edges.
We now introduce some definitions and notations that will be needed for the error estimates.
We denote by ![]() the set of edges of element
the set of edges of element![]() , by
, by ![]() the set of all element edges
the set of all element edges
and the subsets relating to internal, Dirichlet and Neumann edges respectively as
![]() ,
, ![]() and
and
![]() so that
so that![]() .
.
We denote ![]() the set of vertices of
the set of vertices of ![]() and by
and by ![]() the set of all element vertices (that
the set of all element vertices (that
do not lie on the Dirichlet boundary![]() ). Let
). Let ![]() be the set of vertices of
be the set of vertices of![]() , and for
, and for![]() ,
, ![]() and
and ![]() we define the local “patches” of elements as
we define the local “patches” of elements as
![]() ,
, ![]() ,
, ![]() ,
, ![]()
For the lowest order ![]() approximations over a triangular element subdivision,
approximations over a triangular element subdivision, ![]() , so that the interior residual of element K is given by
, so that the interior residual of element K is given by
![]() (3.1)
(3.1)
and the internal residual is approximated by
![]() (3.2)
(3.2)
where ![]() is the
is the ![]() -projection onto
-projection onto![]() .
.
For any edge ![]() of an element
of an element![]() , we define the flux jump as
, we define the flux jump as
![]() (3.3)
(3.3)
where ![]() is a constant function on the inter-element edge
is a constant function on the inter-element edge ![]() and
and ![]() measures the jump of
measures the jump of ![]()
across![]() , that is, for
, that is, for![]() ,
, ![]() and defining
and defining ![]() and
and ![]() to be the outward normals with respect to the edge
to be the outward normals with respect to the edge ![]() from element K and S respectively, we have
from element K and S respectively, we have
![]() (3.4)
(3.4)
The approximation space is denoted by
![]() (3.5)
(3.5)
consisting of edge and interior bubble functions respectively:
![]() (3.6)
(3.6)
where each member of the space is a quadratic (or biquadratic) edge bubble function ![]() that is nonzero on edge E of element K, but non zero valued on all other edges of K.
that is nonzero on edge E of element K, but non zero valued on all other edges of K.
![]() is the space spanned by interior cubic (or biquadratic) bubbles
is the space spanned by interior cubic (or biquadratic) bubbles ![]() i.e.,
i.e.,
![]() (3.7)
(3.7)
where each function is associated with an element K, and is zero on all edges of K, nonzero on the interior of K, and ![]() at the centeroid of K.
at the centeroid of K.
The upshot is that the local problems are always well posed and that for each triangular element a 4 × 4 system of equations must be solved to compute![]() .
.
For an element![]() , the local error estimate is the energy norm of
, the local error estimate is the energy norm of ![]() given by
given by
![]() (3.8)
(3.8)
where ![]() satisfies
satisfies
![]() (3.9)
(3.9)
In the following, we use the short-hand notation ![]() to denote
to denote ![]() -norm of a function
-norm of a function![]() . The Kay and Silvester’s a posteriori error estimation can be read as following:
. The Kay and Silvester’s a posteriori error estimation can be read as following:
Theorem 1. If the variational Equation (2.6) solved with a grid of linear triangular elements, and if the triangle aspect ratio condition is satisfied with![]() , then, the estimator
, then, the estimator ![]() computed via Equation (3.9) satisfies the (global) upper bound property
computed via Equation (3.9) satisfies the (global) upper bound property
![]() (3.10)
(3.10)
where C is independent of ![]() and h and
and h and ![]() is the length of the longest edge of element K.
is the length of the longest edge of element K.
Proof. See the details in [14] .
Theorem 2. If the variational Equation (2.6) with ![]() is solved via either the Galerkin formulation or the SD formulation Equation (2.11), using a grid of linear triangular elements, and if the triangle aspect ratio condition is satisfied, then the estimator
is solved via either the Galerkin formulation or the SD formulation Equation (2.11), using a grid of linear triangular elements, and if the triangle aspect ratio condition is satisfied, then the estimator ![]() computed via Equation (3.9) is a local lower bound for
computed via Equation (3.9) is a local lower bound for ![]() in the sense that
in the sense that
![]() (3.11)
(3.11)
where c is independent of![]() , and
, and ![]() represents the patch of four elements that have at least one boundary edge E from the set
represents the patch of four elements that have at least one boundary edge E from the set![]() .
.
Proof. See the details in [14] .
4. Numerical Experiments
In this section we report three series of numerical experiments with the Streamline Diffusion stabilization method described in Section (2) and an h-adaptive mesh-refinement strategy based on the error estimator analyzed in Section (3). In all the experiments we have used piecewise linear finite elements (i.e., ![]() polynomial degree
polynomial degree![]() ) and we have taken as geometric domain the unit square
) and we have taken as geometric domain the unit square ![]() or
or![]() , although with different boundary conditions. We have considered varying values of the coefficients
, although with different boundary conditions. We have considered varying values of the coefficients![]() ,
, ![]() , and
, and ![]() of the convection-diffusion equation.
of the convection-diffusion equation.
The adaptive procedure consists in solving Equation (2.11) on a sequence of meshes up to finally attain a solution with an estimated error within a prescribed tolerance. To attain this purpose, we initiate the process with a quasi-uniform mesh and, at each step, a new mesh better adapted to the solution of Equation (2.6) must be created. This is done by computing the local error estimators ![]() for all K in the “old” mesh
for all K in the “old” mesh![]() , and refining
, and refining
those elements K* with![]() , where
, where ![]() is a prescribed parameter. In all our expe-
is a prescribed parameter. In all our expe-
riments we have chosen![]() . For other marking strategies, we refer to [27] .
. For other marking strategies, we refer to [27] .
The implementation used in this paper is derived from iFEM [28] . This software package is the successor of AFEM@MATLAB [29] , which contains an advanced refinement tool.
Example 1 (Exponential boundary layer) The first test problem contains an exponential boundary layer. This
problem corresponds to the case of![]() , zero forcing
, zero forcing![]() , Dirichlet boundary condition,
, Dirichlet boundary condition, ![]() and
and
the exact solution is given by
![]() (4.1)
(4.1)
We report the results obtained for ![]() and
and ![]() over the domain
over the domain![]() .
.
Figure 1 shows the successfully refined meshes created in the adaptive process for![]() , as well as the corresponding computed solution. Figure 2 shows the error curves for the exact and estimated errors. Figure 3
, as well as the corresponding computed solution. Figure 2 shows the error curves for the exact and estimated errors. Figure 3
![]()
Figure 1. Adaptive grids (left) and solution (right) obtained for ![]() & d.o.f:3663.
& d.o.f:3663.
![]()
Figure 2. Estimated and exact error curves using![]() .
.
and Figure 4 show analogous results for the same problem with the parameter![]() . The results show that the estimated error is well bounded as described in [22] .
. The results show that the estimated error is well bounded as described in [22] .
Example 2 (Interior layers) We consider Equation (2.1) with ![]() and
and![]() ,
, ![]() ,
,![]() . The forcing term f and boundary condition are determined from the exact solution:
. The forcing term f and boundary condition are determined from the exact solution:
![]() (4.2)
(4.2)
Figure 5 and Figure 6 clearly show that the adaptive method has successfully refined the correct elements using a greater concentration of elements in the interior layer. Figure 7 and Figure 8 show the estimated and exact error curves decrease monotonically for ![]() and
and ![]() respectively.
respectively.
Example 3 (Interior and boundary layers) We consider Equation (2.1) with![]() ,
,
![]() ,
, ![]() and boundary conditions
and boundary conditions
![]()
Figure 3. Adaptive grids (left) and solution (right) obtained for ![]() & d.o.f: 4183.
& d.o.f: 4183.
![]()
Figure 4. Estimated and exact error curves using![]() .
.
![]()
Figure 5. Adaptive grids (left) and solution (right) obtained for ![]() & d.o.f:5523.
& d.o.f:5523.
![]()
Figure 6. Adaptive grids (left) and solution (right) obtained for ![]() with d.o.f:6259.
with d.o.f:6259.
![]()
Figure 7. Estimated and exact error curves using![]() .
.
![]()
Figure 8. Estimated and exact error curves using![]() .
.
![]() (4.3)
(4.3)
Discontinuities at ![]() causes u to have an internal layer of width
causes u to have an internal layer of width ![]() along the line
along the line![]() , with values
, with values ![]() to the left and
to the left and ![]() to the right, as well as a boundary layer along the outflow boundary. We do not include error curves because no analytical solution is known in this case.
to the right, as well as a boundary layer along the outflow boundary. We do not include error curves because no analytical solution is known in this case.
Figure 9 and Figure 10 show some of the successively refined meshes created in the adaptive process for ![]() and
and![]() , as well as the corresponding computed solution.
, as well as the corresponding computed solution.
In the case of ![]() in Example (2) and
in Example (2) and ![]() in Example (3), the adaptive refinement process able to resolve the boundary and interior layers.
in Example (3), the adaptive refinement process able to resolve the boundary and interior layers.
For the case of ![]() in Example (2) and
in Example (2) and ![]() in Example (3), it is hard to fully resolve the internal layers and the numerical solution display a small oscillatory pattern in the internal layer.
in Example (3), it is hard to fully resolve the internal layers and the numerical solution display a small oscillatory pattern in the internal layer.
5. Conclusions
An adaptive finite element scheme for the convection-diffusion equation has been introduced and analyzed. This scheme is based on the Streamline Diffusion Finite element method combined with a Neumann-type error estimator.
Several numerical experiments are reported. For![]() , all of them show the effectiveness of this scheme to capture boundary and inner layers very sharply and without significant oscillations. But in the case of
, all of them show the effectiveness of this scheme to capture boundary and inner layers very sharply and without significant oscillations. But in the case of ![]() in Example (2) and
in Example (2) and ![]() in Example (3), the numerical solution displays small oscillatory pattern in the internal layer which requires a high computing cost to produce an accurate internal layer. In general, it is
in Example (3), the numerical solution displays small oscillatory pattern in the internal layer which requires a high computing cost to produce an accurate internal layer. In general, it is
![]()
Figure 9. Adaptive grids (left) and solution (right) obtained for ![]() with d.o.f:34,897.
with d.o.f:34,897.
![]()
Figure 10. Adaptive grids (left) and solution (right) obtained for ![]() with d.o.f:41,149.
with d.o.f:41,149.
quite evident that our error estimator provides an effective refinement indicator even in the presence of internal layers.