1. Introduction
A truss is a structural object comprising of a stable and systematic arrangement of slender interconnected members. Each member in a truss is straight and is connected at joints. Elements in a truss are arranged in such a pattern so that they produce an efficient, light weight, load-bearing members. Joints in truss carry zero moments since members are connected by frictionless pin. Hence, truss members carry only axial forces which are either in compressive or tensile in nature. Trusses have a high use in modern construction and are used commonly in buildings where support to roofs, floors and internal loadings is readily provided. Steel trusses are most widely used in industrial buildings. These days, most of the trusses are made of steel, however, in some cases timber and concrete trusses are also utilized. The sections used for steel trusses are generally angle sections, square hollow sections, pipe sections, T-sections, C-channel sections, etc. In any case of construction of structure, the main objective is to reduce the cost of the project and fulfill structural requirement. Hence, it becomes necessary to optimize the structure to fulfill the economical requirement. The optimum design of a structure should satisfy various constraint limits, and stress and local stability conditions. The optimum shape of a truss depends not only upon its topology, but it also depends on distribution of element cross-sectional areas. Some of the basic optimization techniques are: Mathematical programming, Optimality criteria, Approximation methods and Fully Stressed Design method. In past, many researchers had carried out research on optimization of truss.
Andrew B. Templemen (1976) introduced theories of dual approach in his paper which showed the implication and usefulness of dual approach [1] . This study considered problem of determining optimal member sizes which minimized weight of a pin jointed truss of fixed geometry which satisfied certain constraints. William Prager (1976) discussed the optimal design of truss which had bars and connected to loaded joints on a horizontal ceiling where single and two alternative loads were considered [2] . Samuel L. Lipson and Krishna M. Agrawal (1974) proposed a complex method of optimization in which geometric and topological variable were included. Method is useful in solving discrete member spectrum which included behavior of members [3] . H. Randolph Thomas Jr. and Daniel M. Brown (1977) presented an algorithm which covered application of optimization method for roof truss system considering the cost function as parameter [4] . Andrew B. Templemen (1983) explained the reason why only some research output could be applied to designing [5] . Rajasekaran (1983) has carried out research on optimal design of industrial roof system by using computer aided technique. He investigated on finding optimal spacing of roof truss of a given span and length to get optimum weight [6] . Ohsaki (1995) carried out a study on optimization of trusses considering displacement and stress constraints in different static loading condition by using the concept of genetic algorithm [7] . John E. Taylor and Mark P. Rossow (1977) presented calculation on optimal design of trusses by considering design variables as constraints and optimally criteria based on strain energy considerations. They have given a formulation to solve number of problem to give optimal member size and member layout by giving location of joints and loads [8] . Surya N. Patnaik and Dale A. Hopkins (1998) presented a paper on fully stressed design by use of analytical and graphical methods and by taking displacement constraints [9] . Lluis Gil and Antoni Andreu (2001) presented a method to give optimum shape and cross section of a plane truss by considering stress constraints and geometrical constraints. They used fully stress design method for the optimization of cross section and conjugate gradient method for optimization of coordinates [10] . Wang et al. (2002) presented a paper on optimization by taking node shift method for 3-dimensional truss in terms of nodal coordinates and elemental cross-section areas. Two typical trusses are examined to illustrate validity of the method [11] . Huan Li Teng Hai-Wen (2010) presented fully stressed design of statically indeterminate truss. His work and calculation can be used as reference for engineering practice [12] . Atai Ahrari and Ali A. Atai (2013) carried out a study on fully stressed design evolution strategy of truss [13] . Ganzreli (2013) presented a paper on fully stressed design method of optimization for determining trusses by taking displacements constraints [14] . Mustafa Sumayah et al. (2015) presented a paper on optimization of plane trusses by using STAAD.Pro software. Six types of trusses were analyzed by taking a group of design constraints that showed structural configuration [15] . Osman Shallan et al. (2014) carried out a study on genetic algorithm for optimum design of plane and space trusses by using nodal deflection as constraints [16] [17] .
In this study, Fully Stressed Design method has been utilized for optimization of Fink Trusses by using STAAD.Pro V8i (SELECT series 5) software. For this, 9 different load cases have been considered for three different spans. The central load for each Fink Truss has been kept constant throughout the analysis. So by the combination of load and spans, the total 81 cases have been analyzed and steel take-off and displacement are calculated. The section used in this study is pipe section.
2. Fully Stressed Design
FSD is probably the most successful of the optimality criteria methods and is accountable for sparking the maximum interest in growing these sorts of methods. This approach is broadly used in the design of structures. It is applicable to problems with only stress and minimum gage constraints.
The optimality criteria statement for FSD is as follows (Ganzreli, 2013):
“For the optimum design, each member of the structure which are not in there minimum gage must be fully stressed under at least one of the design load conditions”.
So when a structure no longer reaches its allowable stress its area can be reduced in order to make it fully stressed. The convergence of FSD can be done through number of iterations.
In this study target stress of 100 MPa has been considered for analysis. Since stress is inversely proportional to the area as shown below in Equation (1),
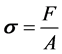 (1)
(1)
where  is stress, F is applied load and A is cross-section area.
is stress, F is applied load and A is cross-section area.
Therefore in FSD cross-sectional area of the member can be given as:
 (2)
(2)
 (3)
(3)
where, 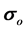 is stress in the older section, Ao is area of the older section,
is stress in the older section, Ao is area of the older section, 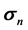 is stress in the required section i.e., 100 MPa, An is area in the newer section. Hence by this formulation area in each member is calculated and target stress is achieved in STAAD.Pro V8i (SELECT series 5) software.
is stress in the required section i.e., 100 MPa, An is area in the newer section. Hence by this formulation area in each member is calculated and target stress is achieved in STAAD.Pro V8i (SELECT series 5) software.
3. Modeling and Analysis of Trusses
Type of Fink Truss analyzed in this study is shown below in Figure 1. In this study three spans have been considered, viz, 10 m, 15 m and 20 m and height is kept constant as 3 m for all cases. Modelling of the trusses have been carried out using STAAD.Pro V8i (SELECT series 5) software.
Properties and geometrical parameters of Fink Truss used are given in Table 1 and Table 3 respectively.
Loading condition taken in this study is given in Table 2. Total numbers of 3 loads are taken 100 kN, 120 kN and 150 kN. The load on central node is kept constant as 100 kN in all cases. Figure 2 shows the position of loads.
![]()
Figure 2. Diagram showing nodal load positions.
![]()
Table 3. Geometrical parameters of Fink Truss.
4. Results and Discussion
FSD was carried out in iterative manner for target stress of 100 MPa and cross sectional areas of the members were noted down. Since the density of steel was known the steel i.e. 7800 kg/m3, steel take off was calculated for the overall truss structure. Pipe section has been used for analysis in this study and thickness of 6 mm is considered. Tables for all cases are prepared. One of the tables for load condition 1 has been given below in Table 4.
![]()
Table 4. Steel take off for loaf case 1 of 10 m span Fink Truss having height 3 m.
For load condition 1 Mass (steel take off) came out to be 1143.035 kg and maximum displacement is 11.541 mm.
Similarly for all cases, tables have been prepared and steel take off and maximum displacement is calculated and graphs are plotted which are shown in Figures 3-8.
Mass and Load case graph for 10m span Fink Truss is shown below.
It is observed that the maximum and minimum masses for 10m span Fink Truss are:
Maximum Mass of the Truss = 1646.117 kg for load case 27, i.e., 150/150/150
Minimum Mass of the Truss = 1143.035 kg for load case 1, i.e., 100/100/100
![]()
Figure 3. Mass and load graph for 10 m span Fink Truss.
![]()
Figure 4. Displacement and load graph for 10 m span Fink Truss.
![]()
Figure 5. Mass and load graph for 15 m span Fink Truss.
![]()
Figure 6. Displacement and load graph for 15 m span Fink Truss.
![]()
Figure 7. Mass and load graph for 20 m span Fink Truss.
![]()
Figure 8. Displacement and load graph for 20 m span Fink Truss.
Graph between deflection and load cases as follows:
From this graph it is observed that:
Maximum deflection for 10 m span Fink Truss = 11.586 mm for load case 17 i.e., 120/150/120.
Minimum deflection for 10 m span Fink Truss = 11.532 mm at load case 27 i.e., 150/150/150.
Mass and Load graph for 15 m span Fink Truss is shown below.
It is observed that the maximum and minimum masses for 15 m span Fink Truss are:
Maximum Mass of the Truss = 3155.26 kg for load case 26 i.e., 150/150/120
Minimum Mass of the Truss = 2203.12 kg for load case 1 i.e., 100/100/100
From this graph it is observed that:
Maximum deflection for 15 m span Fink Truss = 23.325 mm at load case 15 i.e., 120/120/150.
Minimum deflection for 15m span Fink Truss = 20.551 mm at load case 26 i.e., 150/150/120
It is observed that the maximum and minimum masses for 15 m span Fink Truss are:
Maximum Mass of the Truss = 5251.831765 kg for load case 27 i.e., 150/150/150
Minimum Mass of the Truss = 3681.449 kg for load case 1 i.e., 100/100/100
Graph between Displacement and Load cases as follows:
From this graph it is observed that:
Maximum deflection for 20 m span Fink Truss = 36.07 mm at load case 5 i.e., 100/120/120.
Minimum deflection for 20 m span Fink Truss = 36.032 mm at load case 10 i.e., 120/100/100
The total compiled values for all the total no. of 81 cases is shown in Figure 9.
The total compiled values for all the 81 cases for Span and Displacement are shown in the graph below in Figure 10.
![]()
Figure 9. Mass and load graph for total for all 81 cases.
![]()
Figure 10. Displacement and Load graph for total values for all 81 case.
5. Conclusions
In this study, Fully Stressed Design of Fink Trusses have been carried out by using STAAD.Pro V8i (SELECT series 5) software for three different spans and 27 different load cases. The objective of this analysis is to determine the steel take-off and the central deflection of each truss.
The following conclusions can be drawn from Figure 9:
1. For 10 m span Fink Truss having a rise of 3 m, it is observed that as the load cases are varied there is not much variation in the total steel take-off of the truss. As the span is smaller than the other two spans, the overall comparison of steel take-off is obviously less, but within the span there is not much variation. As observed from the study the steel take-off for the load case 100/100/120 is 1333.54 kg and the same for the case 120/120/120 is 1346.93 kg, so there is not much variation in the steel take-off.
2. For 15 m span Fink Truss having a rise of 3 m, it is seen that variation is not much in the steel take-off.
3. For 20 m span Fink Truss having a rise of 3 m, the similar pattern has been observed as in the other two cases. Since it is the biggest span in comparison to the other two, the overall steel take-off will be more.
It is concluded that weight does not always increase with increase in the span or height. Hence, it is necessary for design engineer to optimize the structure to have the best height and span combination to save the material and make the structure economical.
The following conclusions can be drawn out of the above graph in Figure 10:
1. It is observed that the maximum displacement of truss is:
For 10 m span = 11.586 mm, load case 17 (120/150/100);
For 15 m span = 23.324 mm, load case 15 (120/120/150);
For 20 m span = 36.07 mm, load case 5 (100/120/120).
2. For 10 m span Fink Truss there is not much variation in the displacement for all the load cases.
3. For 15 m span Fink Truss there is certain increment in the displacement for the load case 15 (120/120/150).
4. For 20 m span Fink Truss there is a lot variation in the displacement for all the load cases. As for the load case 10 (120/100/100) it is minimum as 36.032 mm and for load case 5 (100/120/120) it is maximum as 36.07 mm.
From displacement graph it is concluded that there is not much variation in the displacement for different load cases for the same span.