Freidlin-Wentzell’s Large Deviations for Stochastic Evolution Equations with Poisson Jumps

Huiyan Zhao^1,2, Siyan Xu³

¹School of Economics and Statistics, Guangzhou University, Guangzhou, China.
²School of Applied Mathematics, Beijing Normal University Zhuhai, Zhuhai, China.
³Faculty of Science, Ningbo University, Ningbo, China.

DOI: 10.4236/apm.2016.610056                

Abstract

We establish a Freidlin-Wentzell’s large deviation principle for general stochastic evolution equations with Poisson jumps and small multiplicative noises by using weak convergence method.

Keywords

Stochastic Evolution Equation, Poisson Jumps, Freidlin-Wentzell’s Large Deviation, Weak Convergence Method

1. Introduction

The weak convergence method of proving a large deviation principle has been developed by Dupuis and Ellis in [1] . The main idea is to get sevral variational representation formulas for the Laplace transform of certain functionals, and then to prove an equi- valence between Laplace principle and large deviation principle (LDP). For Brownian functionals, Boué and Dupuis [2] have proved an elegant variational representation formula (also can be found in Zhang [3] ). For Poisson functionals, we can see Zhang [4] . Recently, a variational representation formula on Wiener-Poisson space has been estab- lished by Budhiraja, Dupuis, and Maroulas in [5] . These type variational representations have been proved to be very effective for both finite-dimensional and infinite-dimen- sional stochastic dynamical systems (cf. [6] - [10] ). The main advantages of this method are that we only have to make some necessary moment estimates.

However, there are still few results on the large deviation for stochastic evolution equations with jumps. In [11] , Röckner and Zhang considered the following type semi-linear stochastic evolutions driven by Lévy processes

they established the LDP by proving some exponential integrability on different spaces. Later, Budhiraja, Chen and Dupuis developed a large deviation for small Poisson perturbations of a more general class of deterministic equations in infinite dimensional ( [12] ), but they did not consider the small Brownian perturbations simultaneously.

Motivated by the above work, we would like to prove a Freidlin-Wentzell’s large deviation for nonlinear stochastic evolution equations with Poisson jumps and Brownian motions. At the same time, nonlinear stochastic evolution equations have been studied in various literatures (cf. [13] - [17] ). So we consider the following stochastic evolution equation:

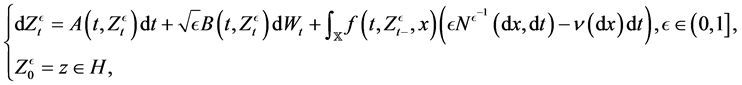
in the framework of a Gelfand’s triple:

where V, H (see Section 2) are separable Banach and separable Hilbert space respec- tively. We will establish LDP for solutions of above evolution equation on

, where is H-valued cádlág function space with the Skorokhod topology. For stochastic evolution equations without jumps, Ren and Zhang [9] and Liu [8] achieved the LDP on () and () respectively. In our case, there are two new difficulties. The first one is to find a sufficient condition to characterize a compact set in 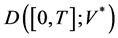(see Proposition 4) instead of Ascoli-Arzelà’s theorem for continuous case, the second one is to control the jump parts. This form of equation contains a large class of (nonliear) stochastic partial differential equation of evolutional type, for applications and examples we refer the reader to [8] , [9] . The equations we consider here are more general than the equations considered in [11] , and we use a different method. We note that, the large deviations for semilinear SPDEs in the sense of mild solutions were considered in paper [18] recently. For other recent research on this topic, see also [12] , [19] .

In Section 2, we firstly give some notations and recall some results from [5] , which are the basis of our paper, and then introduce our framework. In Section 3, we prove the large deviation principle. In the last section, we give an application. Note that notations c, and 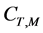below will only denote positive constants whose values may vary from line to line.

2. Preliminaries and Framework

We first recall some notations from [5] .

Let be a locally compact Polish space and denote by the space of all measures on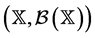, satisfying for every compact. Let

be the space of continuous functions with compact support. is a Polish space endowed with the weakest topology such that for every,

is a continuous function.

Set. Fix and let. Let and denote by the unique probability measure on such that the canonical map, , , is a Poisson random measure with intensity

, where, and are Lebesgue measures on and respectively.

Let G be a real separable Hilbert space and let Q be a positive definite and symmetric trace operator defined on G. Set and. Let be defined by, for. Let W be the coordinate map on defined as. Define. We denote by P the unique probability measure on such that under P:

1) W is a Q-Wiener process;

2) N is a Poisson random measure with intensity measure;

3), are -martingales for every.

We denote by be P-completion of the filtration. From now on, we will work on the probability space with filtration.

Denote by the predictable s-field on with the filtration

on. Let

., de- fine

where

and define a counting process as

For fixed, let

(1)

By [5] , we can define, for a function, and identify g with measure. Besides, is a compact subset of through the superlinear groth of l. We can also consider the to- pology on which makes a compact space.

Remark 1. We note that, for, , in this topology means

, that is, for any,

holds as.

Set and define. Let

(2)

We endow with the weak topology on the Hilbert space such that is a compact subset of.

Let with the usual product topology. Set and let be the space of -valued controls:

Let be a Polish space and let be a set of -valued random variables

defined on by

where is a family of measurable maps from to.

Hypothesis. There exists a measurable map such that the following hold.

1) For, if a family converges in distribution to, then

where Þ denotes the weak convergence.

2) For, let be such that. Then

For, define. Let be

(3)

where.

We have the following important result due to [5] .

Theorem 2. Under the above Hypothesis, satisfies a large deviation prin- ciple with rate function I.

Now we introduce our framework and assumptions.

Let be a real separable Hilbert space. Let V be a reflexive Banach space and be the dual space of V and denotes the corresponding dualization. Identify H with its dual and the following assumptions are satisfied:

1);

2) V is dense in H;

3) there exists a constant c such that for all,;

4).

Let be the space of Hilbert-Schmidt linear operators from G to H, which is a real separable Hilbert space with the inner product

where is an orthonormal basis of G. We denote by the set of all linear operators C mapping into H such that, and the norm.

Let

be progressively measurable. For example, for every, A restricted to

is -measurable.

We assume throughout this paper that:

(H1) Hermicontinuity: For any, and any, the mapping

is continuous.

(H2) Weak monotonicity: There exist such that for all

holds on.

(H3) Coercivity: For all and, there exist such that

holds on.

(H4) For all and, there exists such that

holds on.

(H5) There exists such that for all, and

and

(4)

(H6) There exist some compact, , for all

. For any, is continuous on.

(H7) compactly.

3. Large Deviation Principle

Consider small noise stochastic evolution equation as following:

(5)

Under the assumptions (H1)-(H5), by [15] , [17] , there exists a unique solution in to Equation (5). By Yamada-Watanabe theorem, there exists a measurable mapping such that

We now fix a family of processes, and put

By Girsanov’s theorem, is the unique solution of the following controlled sto- chastic evolution equation:

(6)

Remark 3. For, by (1) and (2), there exists a constant such that for all,

(7)

We will verify that satisfies the Hypothesis with replaced by

. By using the similar method as in [9] , we have the following uniform estimates about.

Lemma 1. There exists a constant such that, for all,

(8)

(9)

In order to characterize a compact set in, we need the following lemma.

Lemma 2. For any and, there exist and such that for any, we have

(10)

Proof. For fixed and any t such that, we have

Therefore

where

For, by (H4), Hölder’s inequality and Lemma 1, we have

where

By (7), we have

So by (9) and dominated convergence theorem, for all, we obtain

For, , by BDG’s inequality, (H5) and Lemma 1, we obtain

and

Hence, for any

By choosing and small enough, then (10) holds immediately.

Proposition 4. For a sequence of -valued random variable, if satisfies the following two conditons:

1) For any, there are, , with

2) For any and, there are, , with

Then is C-tight, that is, is tightness in and if X is a limit point then a.s..

Proof. It’s obvious that (2) implies the following condition (cf. [20] , p. 290). For any and, there are, , with

(11)

where

For the finite family, we can find and such that

Hence, replacing R by in (1) and by in (11), we obtain that they still hold with.

Fix. Let and satisfy

Then

satisfies

By (H7), we have compactly. So, satisfies the conditions of Theorem A2.2 ( [21] , p. 563), then it’s relatively compact in. This implies tightness of.

It remains to prove that if a subsequence, still denoted by, converges in law to some X, then X is a.s. continuous. By taking the same scheme as in Proposition 3.26 (cf. [20] , p. 315) and replacing by in the proof, we complete the proof.

According to Lemma 1 and Lemma 2, we have the following result:

Corollary 1. The sequence is C-tight in.

Lemma 3. Assume that for almost all, weakly converges to in for fixed and there is a -valued process such that

(12)

Then, solves the following equation:

Moreover, we have

(13)

and if in (H2), then

(14)

Proof. We divide our proof into several steps.

Step 1. By Lemma 1, we have

(15)

and

(16)

Therefore, by the strong convergence of to as in (12). We get, for almost all, converges weakly to in H and converges to weakly in; and so we have

(17)

(18)

By (12), (16) and dominated convergence theorem, we have

Thus

(19)

Step 2. In this step, we prove solves Equation (13). By (H4) and (15), we have

(20)

Hence, by (15) and (20), there exist subsequences of, and (still denoted by themselves for simplicity) and, and such that

(21)

(22)

and

(23)

Define

Note that

By taking weak limits and by (19), we can get

Indeed, for any V-valued bounded and measurable process,

By (21), (23) and taking limits for, then we get (see also the proof of (27) and (29) below)

which implies for almost all. Similarly, we have

for almost all.

We only have to prove

(24)

Let. By Itô’s formula

(25)

By (H2)

(26)

as.

We now prove

(27)

Since weakly converges to in (see (2)), then

the last limit follows by using dominated convergence theorem. By (2), (H5), Lemma 1 and (19), we also have

and

Then limit (27) follows.

Moreover, it is easy to get that

(28)

Now we prove the following limit:

(29)

By (H5), Lemma 1 and (19), we have

(30)

where

and

For, by Young inequality, we have

by noting (16) and (19). For, by (4), (H6) and, it’s easy to verify

is a continuous function on with the compact su-

pport, and by the weak convergence of to (see Remark 1) and domi- nated convergence theorem, as. Then (30) goes to 0 as. Similarly, we have

Then, we get (29).

It is obvious that

(31)

Combining (26) to (31) yields that

On the other hand, by Itô’s formula we have

So, we have

which implies (24) by (H1).

Step 3. In this step we prove (13) and (14). Notice that

By Itô’s formula, we have

where

By Lemma 1 and BDG’s inequality, we get

For, we have

Similarly

For, like, we have

Similarly

For, by (H5) and (H6) we have

Assume, then

(32)

Set

then

So

Notice (32), we get (13) and (14) immediately.

We also have the following main lemma.

Lemma 4. There exists a probability space and a sequence (for conve-

nience, still denote by) and

defined on this space and taking value in

with such that:

1) For each, has the same law as

;

2) in, -a.s., as;

3) uniquely solves the following equation:

(33)

Moreover, we have

(34)

and if, then

(35)

Proof. From Corollary 1, we have is C-tight in. By the com- pactness of, the law of in is tight. By Skorok- hod’s embedding theorem, (1) and (2) hold. Since -a.s. and

Then, the other conclusions follow from Lemma 3 and noting for almost all,.

Remark 5. Assume that (H1)-(H7) and hold, we have verified Hypothesis (1) by the above lemma.

For fixed, let and let such that is the unique solution of

We point out that the difference between in the above equation and in (13) is that is not random. We have the following result.

Lemma 5. Assume that (H1)-(H7) and hold. Let, be such that in the weak topology of (see Section 2), then

Proof. Similar to the proofs of Lemma 1 and 2, we can get

is C-tight. As in Lemma 4, there exist a subsequence (still denoted by m) and

satisfying

Combining with this convergence and the method used in the proof of Lemma 3, we have, then the result holds.

Using Remark 5, Lemma 5 and Theorem 2, we obtain the following large deviation principle.

Theorem 6. Under the same assumptions as in Lemma 5, satisfies a large deviation principle with rate function I defined as in (3), i.e. for any

where is the law of in and is.

Remark 7. If, then the conclusion still holds if is replaced by

.

4. Application―Stochastic Porous Medium Equation

Similar to [9] , consider a bounded domain in with smooth boundary. For

, let

The inner product in H is defined by

establish an isomorphism between and. We identify

with the dual space and H, then. There- fore

and the inclusions are compact.

Let. For, denote by

Then and (H1)-(H4) hold (cf. [9] [16] ).

Let. Define

where are Lipschitz continuous on. Let, , and define

where are Lipschitz continuous on. Then B and f satisfy (H5)-(H6).

Consider the following stochastic porous medium equation

Let be the law of in. Then the conclusion of Theorem 6 holds.

Acknowledgements

The authors thank the Editor and the referee for their valuable comments. This work is supported in part by Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ13A010020) and the National Natural Science Foundation of China (Grant No. 11401029).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Dupuis, P. and Ellis, R.S. (1997) A Weak Convergence Approach to the Theory of Large Deviations. Wiley Series in Probability and Statistics: Probability and Statistics. A Wiley-Interscience Publication. John Wiley and Sons, Inc., New York. http://dx.doi.org/10.1002/9781118165904
[2]	Boué, M. and Dupuis, P. (1998) A Variational Representation for Certain Functionals of Brownian Motion. Annals of Probability, 26, 1641-1659.
[3]	Zhang, X. (2009) A Variational Representation for Random Funcionals on Abstract Wiener Spaces. Journal of Mathematics of Kyoto University, 49, 475-490.
[4]	Zhang, X. (2009) Clark-Ocone Formula and Variational Representation for Poisson Functionals. Annals of Probability, 37, 506-529. http://dx.doi.org/10.1214/08-AOP411
[5]	Budhiraja, A., Dupuis, P. and Maroulas, V. (2011) Variational Representations for Continuous Time Process. Annales de l Institut Henri Poincaré Probabilités et Statistiques, 47, 725-747.
[6]	Boué, M., Dupuis, P. and Ellis, R.S. (2000) Large Deviations for Small Noise Diffusions with Discontinuous Statistics. Probability Theory and Related Fields, 116, 125-149. http://dx.doi.org/10.1007/PL00008720
[7]	Budhiraja, A., Dupuis, P. and Maroulas, V. (2008) Large Deviations for Infinite Dimensional Stochastic Dynamical Systems. Annals of Probability, 36, 1390-1420. http://dx.doi.org/10.1214/07-AOP362
[8]	Liu, W. (2010) Large Deviation for Stochastic Evolution Equations with Small Multiplicative Noise. Applied Mathematics & Optimization, 61, 27-56. http://dx.doi.org/10.1007/s00245-009-9072-2
[9]	Ren, J. and Zhang, X. (2008) Freidlin-Wentzell’s Large Deviations for Stochastic Evolution Equations. Journal of Functional Analysis, 254, 3148-3172. http://dx.doi.org/10.1016/j.jfa.2008.02.010
[10]	Zhang, X. (2008) Euler Schemes and Large Deviations for Stochastic Volterra Equations with Singular Kernels. Journal of Differential Equations, 224, 2226-2250. http://dx.doi.org/10.1016/j.jde.2008.02.019
[11]	Röckner, M. and Zhang, T. (2007) Stochastic Evolution Equations of Jump Type: Existence, Uniqueness and Large Deviation Principles. Potential Analysis, 26, 255-279. http://dx.doi.org/10.1007/s11118-006-9035-z
[12]	Budhiraja, A., Chen, J. and Dupuis, P. (2013) Large Deviations for Stochastic Partial Differential Equations Driven by a Poisson Random Measure. Stochastic Processes and their Applications, 123, 523-560. http://dx.doi.org/10.1016/j.spa.2012.09.010
[13]	Gyöngy, I. and Krylov, N.V. (1980) On Stochastic Equations with Respect to Semimartingales I. Stochastics, 4, 1-21. http://dx.doi.org/10.1080/03610918008833154
[14]	Gyöngy, I. and Krylov, N.V. (1982) On Stochastic Equations with Respect to Semimartingales II, Ito Formula in Banach Spaces. Stochastics, 6, 153-174. http://dx.doi.org/10.1080/17442508208833202
[15]	Gyöngy, I. (1982) On Stochastic Equations with Respect to Semimartingales III. Stochastics, 7, 231-254. http://dx.doi.org/10.1080/17442508208833220
[16]	Ren, J., Röckner, M. and Wang, F. (2007) Stochastic Generalixed Porous Media and fast Diffusion Equation. Journal of Differential Equations, 238, 118-152. http://dx.doi.org/10.1016/j.jde.2007.03.027
[17]	Zhao, H. (2009) On Existence and Uniqueness of Stochastic Evolution Equation with Poisson Jumps. Statistics & Probability Letters, 79, 2367-2373. http://dx.doi.org/10.1016/j.spl.2009.08.006
[18]	Yang, X., Zhai, J. and Zhang, T. (2015) Large Deviations for SPDEs of Jump Type. Stochastic and Dynamics, 15.
[19]	Dadashi, H. (2013) Large Deviation Principle for Mild Solutions of Stochastic Evolution Equations with Multiplicative Lévy Noise. arXiv:1309.1935v1 [math.PR] http://arxiv.org/pdf/1309.1935.pdf
[20]	Jacod, J. and Shiryaev, A. (1980) Limit Theorems for Stochastic Processes. Springer-Verlag, New York.
[21]	Kallenberg, O. (2002) Foudations of Modern Probability. 2nd Edition, Applied Probability Trust. http://dx.doi.org/10.1007/978-1-4757-4015-8