Equilibrium Positions of a Cable-Connected Satellites System under Several Influences

Santosh Kumar, Sangam Kumar^*

P. G. Department of Physics, L. S. College, B. R. A. Bihar University, Muzaffarpur, Bihar, India.

DOI: 10.4236/ijaa.2016.63024                

Abstract

The present paper deals with the study of equilibrium positions of the motion of a system of two artificial satellites connected by a light, flexible, inextensible and non-conducting cable under the influence of solar radiation pressure, earth’s oblateness, shadow of the earth and air resistance. Here, we study the case of circular orbit of the centre of mass of the system. We derive differential equations of motion of the system. General solutions of the differential equations are beyond the reach. On the other hand, the general solutions do not serve our purpose. Jacobian integral of the system has also been obtained. Thereafter equilibrium positions of the motion of the system have been obtained.

Keywords

Equilibrium Positions, Two Cable-Connected Satellites, Circular Orbit

Received 19 May 2016; accepted 4 September 2016; published 8 September 2016

1. Introduction

We study the equilibrium positions of the motion of a system of two cable-connected artificial satellites under the influence of solar radiation pressure, earth’s oblateness, shadow of the earth and air resistance. The influence of the above mentioned perturbations on the system has been studied singly and by a combination of any two or three of them by various workers, but never conjointly all at a time. Therefore, these could not give a real picture of motion of the system. This fact has initiated the present research work. The case of circular orbit of the centre of mass of the system is discussed. Shadow of the earth is taken to be cylindrical and the system is allowed to pass through the shadow beam. The satellites are connected by a light, flexible, inextensible and non-conducting cable. The satellites are taken as material particles. Since masses of the satellites are small and distances between the satellites and other celestial bodies are very large, the gravitational forces of attraction between the satellites and other celestial bodies including the sun have been neglected.

The present work is an attempt towards the generalization of work done by Beletsky and Novikova [1] and Beletsky and Novoorebelskii [2] . They studied the motion of a system of two satellites connected by a light, flexible and inextensible string in the central gravitational field of force relative to its centre of mass. This study assumed that the two satellites are moving in the plane of the centre of mass. Das et al. [3] studied the effect of magnetic force on the motion of a system of two cable-connected satellites in orbit. Kumar and Bhattacharya [4] studied the stability of equilibrium positions of two cable-connected satellites under the influence of solar radiation pressure, earth’s oblateness and earth’s magnetic field. Kumar et al. [5] obtained the equations of motion of a system of two cable-connected artificial satellites under the influence of solar radiation pressure, earth’s oblateness and shadow of the earth. Singh and Demin [6] and Singh [7] investigated the problem in two and three dimensional cases.

2. Equations of Motion and Jacobian Integral of the System

We write the equations of motion of one of the satellites when the centre of mass moves along Keplarian elliptical orbit in Nechvile’s co-ordinate system [8] as Prasad and Kumar [9] .

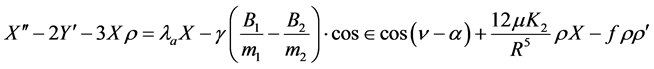
And

(2.1)

With the condition of constraint

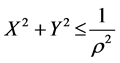(2.2)

Also,

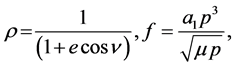
(2.3)

m₁ and m₂ are masses of the two satellites. B₁ and B₂ are the absolute values of the forces due to the direct solar pressure on m₁ and m₂ respectively and are small. p is the focal parameter. m is the product of mass of the earth and gravitational constant. l is undermined Lagrange’s multiplier. 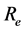is equatorial radius of the earth. 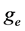is the force of gravity. W is angular velocity of the earth’s rotation. a_R is the earth’s oblateness. 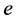is ecentricity of the orbit of the centre of mass. v is the true anomaly of the centre of mass of the system. 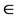is inclination of the oscillatory plane of the masses m₁ and m₂ with the orbital plane of the centre of mass of the system. a is the inclination of the ray. γ is a shadow function which depends on the illumination of the system of satellites by the sun rays. If γ is equal to zero, then the system is affected by the shadow of the earth. If γ is equal to one, then the system is not within the said shadow. 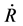is the first order time derivative of R. R is the modulus of position vector of the centre of mass of the system. c₁ and c₂ are the Ballistic coefficients. is the average density of the atmosphere. Prime denotes differentiation with respect to v.

If motion of one of the satellites m₁ be determined with the help of equations (2.1), motion of the other satellite of mass m₂ can be determined by Prasad and Kumar [9] .

(2.4)

where, 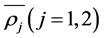is the radius vector in the centre of mass System.

In the case of circular orbit, we put, and in equations (2.1) and write

And

(2.5)

With the condition of constraint

(2.6)

In the case of loose string, we see that, and m₁ moves inside the circle

; whence (2.7)

The system of two satellites is allowed to pass through the shadow beam during its motion. Let us assume that is the angle between the axis of the cylindrical shadow beam and the line joining the centre of the earth and the end point of the orbit of the centre of mass within the earth’s shadow, considering the positive direction towards the motion of the system. The system starts to be influenced by the solar pressure when it makes an angle with the axis of the shadow beam and remains under the influence of solar pressure till it makes an angle with the axis of the cylindrical shadow beam. Thereafter, the system will enter the shadow beam and the effect of solar pressure will come to an end.

Next, the small secular and long periodic effects of the solar pressure together with the effects of the earth’s shadow on the system may be analysed by averaging the periodic terms in (2.5) with respect to from to for a period when the system is under the influence of the sun rays directly i.e. and from to for a period when the system passes through the shadow beam i.e..

Thus after averaging the periodic terms of (2.5) we write the equations (2.5) as

And

(2.8)

For the case of loose string, we use and write the above equations (2.8) as

And

(2.9)

These equations do not contain the time explicity. Therefore, Jacobian integral of the motion exists.

Multiplying the first and second equations of (2.9) by X' and Y' respectively, adding them and then integrating the final equation, we get the Jacobian integral in the form

(2.10)

The surface of zero velocity can be obtained in the form

(2.11)

constant of Integration called Jacobian constant.

We, therefore, conclude that satellite moves inside the boundary of different curves of zero velocity, represented by (2.11) for different values of Jacobian constant.

3. Equilibrium Solution of the Problem

We have obtained a set of equations (2.9) for motion of the system in the rotating frame of reference. It is assumed that the system is moving with the effective constraint and the connecting cable of the two satellites always remains tight.

The equilibrium positions of motion of the system are given by the constant values of the co-ordinates in the rotating frame of reference. Let us take

and (3.1)

and are constant, give the equilibrium positions. Therefore, we get

;

; (3.2)

Putting (3.2) in the set of equations (2.9), we get

And

(3.3)

Actually it is very difficult to obtain the solution of (3.3). Hence, we are compelled to make our approaches with certain limitations. In addition to this, we are interested only in the case of the maximum effect of the earth’s shadow on motion of the system.

In the further investigation, we put and as because or cannot be zero. Clearly equations (3.3) become

And

(3.4)

All the two equations of (3.4) are independent of each other.

With the help of the two equations of (3.4), we get the equilibrium position as

(3.5)

4. Conclusion

The equilibrium position has wide applications in solving problems of stability of a cable-connected satellites system in orbit. It will also state whether the motion of the system is continuous or not. We also write Jacobian integral of motion of the system. The work may be further modified, if wobbling and nutation of the orbit of the system are taken into account.

Acknowledgements

We acknowledge the support of Centre of Fundamental Research in Space Dynamics and Celestial Mechanics (CFRSC), Delhi. We are also thankful to Prof. R.K. Sharma from Thiruvanathapuram for his encouragement and support.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Beletsky, V.V. and Novikova, E.T. (1969) About the Relative Motion of Two Connected Bodies in Orbit. Kosmicheskie Issledovania, 7, 377-384.
[2]	Beletsky, V.V. and Novoorebelskii, A.B. (1969) Existence of Stable Relative Equilibria for an Artificial Satellite in a Model Magnetic Field. Institute of Applied Mathematics, Academy of Sciences of the U. S. S. R., Soviet Astronomy, Vol. 17, 213-220.
[3]	Das, S.K., Bhattacharya, P.K. and Singh, R.B. (1976) Effect of Magnetic Force on the Motion of a System of Two Cable-Connected Satellites in Orbit. Proceedings National Academy of Science, India, 46, 287-299.
[4]	Kumar, S. and Bhattacharya, P.K. (1995) Stability of Equilibrium Position of Two Cable-Connected Satellites. In: Bhatnagar, K.B. and Ishwar, B., Eds., Proceedings Workshop on Space Dynamics and Celestial Mechanics, Muzaffarpur, India, 71-74.
[5]	Kumar, S., Srivastava, U.K. and Bhattacharya, P.K. (2005) Equations of Motion of a System of Two Cable-Connected Artificial Satellites under the Influence of Solar Radiation Pressure, Earth’s Oblateness and Shadow of the Earth. Proceedings Mathematical Society, Banaras Hindu University, Varanasi, 21, 51-61.
[6]	Singh, R.B. and Demin, V.G. (1972) About the Motion of a Heavy Flexible String Attached to the Satellites in the Central Field of Attraction. Celestial Mechanics, 6, 268-277.
[7]	Singh, R.B. (1973) Three Dimensional Motion of a System of Two Cable-Connected Satellites in Orbit. Astronautica Acta, 18, 301-308.
[8]	Nechvile, V. (1926) Surune Nouvelic Forme Des Equations Differentielies Du Problem Restriint Elliptique. Academy Paris Compte Rendus, 182, 310-322.
[9]	Prasad, J.D. and Kumar, S. (2011) Equations of Motion of a System of Two Cable-Connected Artificial Satellites Under the Influence of Earth’s Magnetic Field, Earth’s Shadow, Solar Radiation Pressure and Eatrh’s Oblateness. Journal Purvanchal Academy of Sciences, Jaunpur, India, 17 (Physical Science), 27-34.