Another Important Parameter’s Research on Estimating Self-Similarity ()
Received 20 June 2016; accepted 19 August 2016; published 22 August 2016

1. Introduction
It is a truth universally acknowledged that the Self-Similarity of network traffic has demonstrated that network data exhibit two major attributes: scale-invariant and the slow power-law decrease of the autocorrelation function [1] . Especially, Hurst (H) is a key parameter that can describe statistical feature of data and the second-or- der statistics in the self-similar process [2] . In general, the model built here exhibits long-range dependence when H is between 0.5 and 1, and the degree of similarity is growing with the increase of H. The model shows short-range dependence when H = 0.5 and the network is instable when H < 0.5. Therefore, estimating the Hurst parameter effectively and accurately plays a significant role in analyzing the performances and detecting the abnormities of networking.
Recently, people have designed a number of approaches to evaluate the Hurst parameter, such as R/S method, variance-time analysis, periodogram method [3] - [5] and the method based upon the Discrete Fractional Gaussian Noise (DFGN) Model and Haar wavelet [6] . All these methods accurately estimate the Hurst parameter to some degree. However, most of the current models describe the extremely complicated Self-Similarity of the network based on the only H parameter, which might lead to inaccurate simulation and sub-optimal protocol performance. This issue has attracted much concern in telecommunications. Darryl Veitch and Patrice Abry [7] point out that there exists another parameter in the research of self-similarity and introduced it initially. However, they did not come to a certain and clear conclusion. In addition, Wu Yuanming [8] also mentions that it is inappropriate to describe the self-similarity of network under the condition of only Hurst parameter.
Therefore, unlike most existing studies that primarily focus on the estimating of H, we not only improve the estimator for the H, but also make a comparison and analysis between Hurst parameter and cf parameter in this paper. What’s more, some detail comparison figure between H and cf is displayed under the reasonable and additional technical idealization through the wavelet method and discrete wavelet decomposition. Based on the results, it is shown that the cf parameter also plays a key role in measuring the self-similarity of networking traffic.
The remainder of the paper is set out as follows. Section 2 presents the mathematical definitions and properties of LRD. And we present the proposed method for estimating the Hurst parameter and cf parameter of second-order self-similar process. In Section 3, the simulation results and deductions of experiments on the basis of wavelet method are analyzed. And concluding remarks and further research directions are finally presented in Section 4.
2. Preliminaries
The network traffic in mathematics can be characterized as a random process, reflecting the self-similarity in the structure of network traffic on different time scales. The self-similarity process has complicated qualities and one of the important character is long-range dependence (LRD) [9] [10] . And the definition of LRD is related to the H parameter and cf parameter, which can be described as follows:
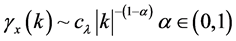 (1)
(1)
Equivalently, it can be defined as the power-law divergence at the origin of its spectrum:
 (2)
(2)
where,  satisfies, in the case of discrete time process:
satisfies, in the case of discrete time process:
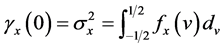 (3)
(3)
and 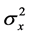 is the variance of (or power) of
is the variance of (or power) of .
.
Apparently, each of these definitions includes two parameters: or
or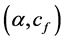 , respectively, which are equivalent as
, respectively, which are equivalent as
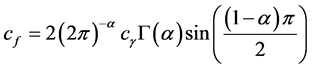 (4)
(4)
where, 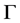 is the Gamma function, and in each pair
is the Gamma function, and in each pair 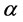 is closely related to the Hurst parameter:
is closely related to the Hurst parameter:
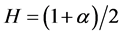 (5)
(5)
According to the reference of [7] , we can get the relationship between 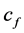 and
and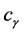 :
:
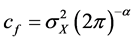 (6)
(6)
Consequently, the expression of ![]() is as follows [11] [12] :
is as follows [11] [12] :
![]() (7)
(7)
The long-range dependence of networking traffic was analyzed by the wavelet decomposition coefficients in wavelet estimation methods [13] [14] . It was divided into approximate and detail part through the discrete wave- let transaction, in which the approximate part means the low frequency of wavelet and the detail part means the high frequency of wavelet [15] [16] . The definition is as follows.
![]() (8)
(8)
where, the ![]() is the inner product of
is the inner product of ![]() and
and ![]()
![]() (9)
(9)
And with the spectrum estimation method, the energy spectrum of ![]() in
in ![]() is
is
![]() (10)
(10)
where, ![]() refers to the wavelet coefficients in the j scales of wavelet decomposition. And the following expression will be got according to the definition of Self-Similarity [17] [18] .
refers to the wavelet coefficients in the j scales of wavelet decomposition. And the following expression will be got according to the definition of Self-Similarity [17] [18] .
![]() (11)
(11)
where, α comes from the equation (5) and ![]() is the Chi-square variable of decomposition scale j.
is the Chi-square variable of decomposition scale j.
![]() (12)
(12)
Therefore, we can get the curve graph about j and![]() . The slop of the curve can be expressed as follows:
. The slop of the curve can be expressed as follows:
![]() (13)
(13)
3. Simulation Result and Analysis
3.1. The Simulation of Self-Similarity Networking Traffic
The networking traffic model simulates the actual networking traffic, which is the basis for analyzing networking performance, predicting networking traffic and designing networking destruction. Recently, there are many Self-Similarity networking traffic models [19] . Such as ON/OFF model, FBM/FGN model, FARIMA model and GARIMA MODEL, etc. Considering the model stability and algorithm simplicity, this paper adopts the Fractal Gaussian Noise (FGN) model [20] - [22] . Based on Fast Fourier Transform (FFT), the spectral density function of Fractal Brownian motion (FBM) is constructed firstly. Then a first-order difference is made to get the FGN sequence. Lastly, we get the simulation of Self-Similarity networking traffic process by setting appropriate H parameter. This paper makes two typical Self-Similarity traffic simulation for H = 0.6 and H = 0.7, and the simulation is as follows:
In Figure 1 and Figure 2, they respectively show the simulation of network traffic with H = 0.6 and H = 0.7. Where the abscissa points out that the length of sample is 1024 and the ordinate represents the random results from the Fractal Gaussian Noise process. The simulation of network traffic has self-similarity when H = 0.6, and it has better self-similarity when H = 0.7.
![]()
Figure 1. FGN sequence with the sample length of 1024 and H = 0.6.
Figure 1 and Figure 2 show the FGN sequence with different Self-Similarity character. In the next, when estimating the Hurst parameter, the wavelet decomposition coefficients of FGN sequence would be used.
In Figure 3 and Figure 4, they show the simulation results of discrete wavelet decomposition when the Hurst parameter in theory of the signal sequence is 0.6. The simulation results are given in Figure 3 when the decomposition scale is 1 and 2, and the ones are shown in Figure 4 when 3 and 4. This decomposition results will be used in the calculation to the actual value for Hurst parameter and cf parameter.
In Figure 5 and Figure 6, they show the simulation results of discrete wavelet decomposition when the Hurst parameter in theory of the signal sequence is 0.7. The simulation results are given in Figure 5 when the decomposition scale is 1 and 2, and the ones are shown in Figure 6 when 3 and 4.
![]()
Figure 2. FGN sequence with the sample length of 1024 and H = 0.7.
![]()
Figure 3. High frequency part of wavelet decomposition for H = 0.6 FGN sequence (scales 1 and 2).
![]()
Figure 4. High frequency part of wavelet decomposition for H = 0.6 FGN sequence (scales 3 and 4).
![]()
Figure 5. High frequency part of wavelet decomposition for H = 0.7 FGN sequence (scales 1 and 2).
![]()
Figure 6. High frequency part of wavelet decomposition for H = 0.7 FGN sequence (scales 3 and 4).
From Figures 3-6 the wavelet decomposition for H = 0.6 and H = 0.7 are presented. The sequence length is reduced to the half of the original sequence and the decomposition coefficients will be used in estimating the self-similarity parameter in the next.
3.2. Parameter Estimation Based on the Wavelet Estimating Method
According to the relevant definition in section 2, Figure 7 and Figure 8 are the simulation results with different parameters based on the wavelet estimating method. The abscissa represents the decomposition scales j and the ordinate is ![]() by the formula (10). Specially, the slop of the graph is
by the formula (10). Specially, the slop of the graph is ![]() = 2H − 1 and thus the estimation of two parameters can be obtained.
= 2H − 1 and thus the estimation of two parameters can be obtained.
In Figure 7 and Figure 8, they respectively represent the simulation result of wavelet method for H = 0.6 and H = 0.7 in theory. The abscissa of the figure shows the decomposition scales of discrete wavelet decomposition and the ordinate refers to the related expression according the definition in Section 2. And the dotted line represents the original data, the solid line represents the fitting data after linear approximation. We can get the actual value of Hurst parameter and cf parameter through the curve’s slope and related expression in Figure 7 and Figure 8.
In Figure 7 and Figure 8, H and cf parameter by the slop of curve are estimated based on the wavelet decomposition. When the theoretical value of H is 0.6 and the actual value is 0.602, the actual value of cf is 5.614. Likewise, when the theoretical value of H is 0.7 and the actual value is 0.680, the actual value of cf is 2.112. Obviously, the difference between theoretical value and actual value is small. The wavelet decomposition is an unbiased and efficient method.
3.3. Analysis about Theoretical and Actual Value of H and Cf Parameter
In Table 1, the theoretical and actual value of H and cf parameter are analyzed. According to eight different
![]()
Figure 7. Parameter estimation for H = 0.6 FGN sequence.
![]()
Figure 8. Parameter estimation for H = 0.7 FGN sequence.
![]()
Table 1. Analysis about the theoretical and actual value of H and cf parameter.
parameters, the different results of eight group data are shown in Table 1.
Where, m means the difference between the theoretical and actual value of H parameter and v means the difference between the theoretical and actual value of cf parameter. We can also get Figure 9, Figure 10 according to Table 1.
In Figure 9, it shows the comparison results between theoretical and estimated value of H vividly. Where the abscissa means the group numbers of comparing is 8 and the ordinate describe the range of H value. And the dotted line represents theoretical value, the solid line represents the estimate value. Obviously, the H value is growing with the change of self-similarity of network traffic.
In Figure 10, it shows the comparison results between theoretical and estimated value of cf vividly. Where the abscissa means the group numbers of comparing is 8 and the ordinate describe the range of cf value. And the dotted line represents theoretical value, the solid line represents the estimate value. Obviously, the cf value is declining with the change of self-similarity of network traffic.
![]()
Figure 9. Comparison between theoretical and estimated value of H.
![]()
Figure 10. Comparison between theoretical and estimated value of cf.
It can be seen the estimated result of H and cf by wavelet method shows high accuracy. Figure 9 and Figure 10 show the different trend of H and cf parameter, namely, the value of H parameter is increasing and the value of cfparameter is decreasing with the change of self-similarity of network traffic.
4. Conclusions
The accurate estimation of self-similar characteristic parameters is the basis to improve Internet analysis and design. This paper makes a lot of theoretical analysis and numerical calculation on the basis of wavelet decomposition method. Not only estimating the H parameter, but also researching another important parameter cf. Moreover, it reveals the fact that cf parameter has important relationship with the Self-Similarity of networking traffic. The Self-Similarity degree is growing with the increasing of H when![]() . However, The Self-Simila- rity degree is growing with the decreasing of
. However, The Self-Simila- rity degree is growing with the decreasing of ![]() when
when![]() . It can be seen that the cf parameter plays a crucial role for estimating the Self-Similarity degree of networking traffic. Therefore, we should considerate both H parameter and cf parameter in the future research. So it is not very accurate to take cf as a constant in some article. This paper adopts FGN model and wavelet estimating method, so we also need further research to show the character of cf parameter for other calculation.
. It can be seen that the cf parameter plays a crucial role for estimating the Self-Similarity degree of networking traffic. Therefore, we should considerate both H parameter and cf parameter in the future research. So it is not very accurate to take cf as a constant in some article. This paper adopts FGN model and wavelet estimating method, so we also need further research to show the character of cf parameter for other calculation.
In the end, this paper verified a novel parameter cf for estimating the self-similarity of networking traffic. Through the fractional Gaussian Noise model and wavelet method, we get lots of simulation results that show the better performance of cf parameter in networking traffic. In addition, it show the important role of cf parameter for describing self-similarity. In the future research, we should estimate H parameter and cf parameter together to measure the self-similarity of networking traffic better.