Research of Fresh Agricultural Products Transverse Replenishment and Deployment in Supermarket Chains ()
Received 6 June 2016; accepted 16 August 2016; published 19 August 2016

1. Introduction
As we all know, agricultural products are the most common and essential food in our daily life, which the safety and freshness are the first condition in the residents’ consumption. With the economic and social development and the improvement of people’s living standards, consumer demand for fresh agricultural products experienced the process of change from quantity to quality. People are in favor of more safety, environmentally protective, green, organic agricultural products. When consumers buy fresh agricultural products, fresh, green, organic, health products are taken into consideration. Usually, the main sources of the supply of fresh agricultural products include farmers’ markets and supermarkets. Compared with farmers’ markets and others, supermarkets are more secure in fresh quality and security. Unified procurement, processing, distribution and strict checks of various aspects let it meet the special requirements in the circulation with irreplaceable advantages. Therefore, supermarket chains become the primary place for consumers to buy fresh agricultural products. However, as more and more people choose to go to the supermarket chains to buy fresh agricultural products, the uncertainty of demand for fresh produce leads to the inaccurate forecasts of supermarket for fresh agricultural products demand. Thus, to a certain extent, this causes the stockpiles or shortages of fresh agricultural products of supermarket, affects the consumer demand for fresh agricultural products, and finally causes some damage of the supermarkets interests. Therefore, research of the transverse replenishment policy of supermarket chains fresh agricultural products can not only ensure the individual needs of consumers for fresh agricultural products, improve customer satisfaction, but also reduce the inventory costs and improve the profits of supermarket chains, make the supermarket chains healthy and fast organic development.
Up to now, researches about the fresh agricultural products transverse replenishment and deployment in supermarket chains are also less. Existing literatures has done some related researches about the shortage, surplus and replenishment of fresh agricultural products.
Wang Weixing (2006) [1] constructed a optimal ordering inventory model under multi-stage continuous demand for perishable products, and started to get the optimal total cost from global suppliers, manufacturers and retailers tripartite. Shui Wenbing, He Min and He Mingwei (2012) [2] developed a multi-product location-inve- ntory model based on the coordinated replenishment multi-product inventory control policy. The minimum of the sum of location cost, transport cost and inventory cost was taken as the objective function of the model, and location number, service scope and inventory control parameters of distribution centers were chosen as the decision variables. Chaaben Kouki et al. (2015) [3] established inventory control model, which contributed to the literature by providing a simple and effective algorithm to compute the best (r, Q) parameters that minimized the total cost. Yiyan Qin et al. (2014) [4] considered the pricing and lot-sizing problem for products with quality and physical quantity deteriorating simultaneously, and designed the optimal model to investigate the deterioration inventory of fresh produce and foods. Biswajit Sarkar and Sumon Sarkar (2013) [5] expanded an inventory model for deteriorating items with stock-dependent demand to determine the optimal cycle length of each product such that the expected total cost (holding, shortage, ordering, deterioration and opportunity cost) was minimized. Yu-Ping Leea and Chung-Yuan Dyeb (2012) [6] formulated a deteriorating inventory model with stock- dependent demand by allowing preservation technology cost as a decision variable in conjunction with replacement policy to find the optimal replenishment and preservation technology investment strategies while maximizing the total profit per unit time. Joaquín Siciliaa et al. (2014) [7] studied a deterministic inventory system for items with a constant deterioration rate. They considered the ordering cost, the holding cost, the backlogging cost, the deteriorating cost, and the purchasing cost in the inventory management and proposed an approach to minimize the total cost per inventory cycle. Hardik N. Soni (2013) [8] formulated a mathematical model and then some useful theoretical results have been derived to characterize the optimal solutions for non-zero and zero ending inventory system. Chih-Te Yang (2014) [9] developed an inventory model under a stock-dependent demand rate and stock-dependent holding cost rate with relaxed terminal conditions to determine the optimal order quantity and the ending inventory level such that the total profit per unit time was maximized for the retailer. Kun-Shan Wua et al. (2006) [10] considered a problem of determining the optimal replenishment policy for non-instantaneous deteriorating items with stock-dependent demand. Chun-Tao Chang et al. (2010) [11] amended Wu et al.’s model by changing the objective to maximizing the total profit and set a maximum inventory level in the model to reflect the facts that most retail outlets have limited shelf space. They relaxed the restriction of the zero ending inventory when shortages were not desirable then established the theoretical results and provided an algorithm to find the optimal solution. Chia-Hsien Su (2012) [12] established a two-echelon
inventory model to encourage sales the supplier offers trade credit to the retailer. And the decision variables include: replenishment cycle time, the time taken to run out of stock and the number of lots delivered from the supplier to the retailer. Parviz Fattahi et al. (2015) [13] proposed a bi-objective multi-product (r, Q) inventory model in which the inventory level is reviewed continuously. The aim of them is to find the optimal value for both order quantity and reorder point through minimizing the total cost and maximizing the service level of the proposed model simultaneously. K. Inderfurth and G. P. Kiesmüller (2015) [14] proposed two novel approaches to derive optimal and near-optimal numerical values for the critical stock level, minimizing the average holding and backorder cost for a given inflation factor. Han Zhu et al. (2015) [15] considered a single-item periodic-review stochastic inventory system with both minimum order quantity (MOQ) and batch ordering requirements. Ali Cheaitou et al. (2014) [16] proposed a single-product, stochastic, two-period inventory control model, which combines demand forecast updating with the flexibility of two supply sources. Gitae Kim et al. (2015) [17] presented a multi-period news vendor model, and the problem is formulated as a multi-stage stochastic programming model with integer recourse decisions to optimize the total logistic cost for perishable products. Cinthia Pérez and Joseph Geunes (2014) [18] analyzed an inventory replenishment model with two transportation modes so as to reduce the inventory cost.
According to the literature review, we can get that previous scholars have made some research on inventory management and replenishment strategy of the supermarket chains fresh agricultural products, but only focused on individual supermarkets to find the optimal strategy to achieve a certain type of supermarket inventory management and not apply the transverse replenishment strategy to the inventory management. In this paper, it will regard all sub supermarket stores of the supermarket chains as a system. Then, the transverse replenishment strategy will be applied. Not only to solve each of the stores of fresh agricultural products inventory costs and restocking fee how to achieve the optimal, more emphasis on system overall inventory replenishment strategy optimal, and system of replenishment goods optimal strategy to prior to a single store replenishment goods optimal strategy. Through the regulation and supervision of the store inventory, supermarket chains can effectively reduce the overall cost of fresh agricultural products inventory, improve the profit margins of fresh agricultural products.
2. Situation Analysis of the Replenishment and Deployment of Supermarket Chains Fresh Agricultural Produce
To complete this study, large supermarket chains in Beijing was investigated. There are several main survey questions: the order cycle of fresh agricultural products, the order amount of fresh agricultural products, whether it will be out of stock or the surplus goods and so on.
2.1. Findings
The survey found that the order cycle of most fresh agricultural products in supermarket chains is once a day. Resupply fresh agricultural products every morning before the open of stores, and with supply schedule. Only the order amount of fresh agricultural products of the sub supermarket chains store surveyed reach 1 ? 20,000 Yuan. The suppliers of this supermarket chains are the surrounding two distribution centers. The supermarkets form strategic partnerships with them, fixed to supply the appropriate amount of fresh agricultural products to the supermarket chains every day.
The maximum time of daily sales of fresh agricultural products is from nine to ten o’clock in the morning and from five to nine five o’clock in the afternoon. The reason for this phenomenon is that in the morning, the elderly choose to in part to purchase the relatively high-quality fresh agricultural products considering the advantage and the freshness of it, but in the afternoon, it is time of coming off duty of white-collar workers, so that the fresh agricultural products is more sales in the period of time.
In addition, the order types of fresh agricultural products in supermarket chains will change with the seasons. The types of fresh agricultural products are with seasonal fruits and vegetables, supplemented by a small amount of off-season fruits and vegetables. Usually there will be shortage or surplus situation are these off-season fruits and vegetables.
2.2. Traditional Solutions for Shortage or Surplus of Fresh Agricultural Products Problems
Supermarket chains in different geographical reasons, traffic conditions, household type, consumption levels and the size of their size, is leading to the different selling degrees of fresh agricultural products. Some supermarket owns surplus of fresh agricultural products because there is less people to buy fresh agricultural products, some supermarkets occur shortage phenomenon because there are more people to buy fresh agricultural products. Fresh agricultural products are easy to spoilage due to its own characteristics, which is a special class of commodities with shortest ordered period in supermarkets. And because the order cycle of fresh agricultural products category is very short, so when there is shortage phenomenon, just waiting for the replenishment by suppliers or self-built distribution center. But such an approach will result in the loss of profit which could be got, and this will reduce the supermarket customer service levels, result in the decrease of customer satisfaction, the reduction of source, and decline the purchase price. In addition, in order to obtain a certain income, the supermarket chains will give the discount when sales the surplus of fresh agricultural products. However, this approach would result in the loss of supermarket chains profits. And if using such methods, in the remaining amount of supermarket fresh produce more, it would not sale all the surplus of fresh agricultural products at the time of the arrival of the next order cycle. Also, when new merchandise is reached, the surplus of fresh agricultural products is easy to become the backlog commodities that cannot be sold, resulting in greater losses.
3. Feasibility Analysis of Transverse Replenishment Method
It is a relatively new approach that transverse replenishment thinking applied to the replenishment of fresh agricultural products in supermarket chains. That conduct transverse replenishment of fresh agricultural products between supermarket stores is when there is shortage, or surplus of supermarket stores, appropriate to transport the surplus fresh agricultural products of the supermarket stores to the shortage fresh agricultural products of the supermarket stores in some period of time, thus timely and effectively solving the shortage, or surplus problems of fresh agricultural products of the supermarket stores. Through the transverse replenishment, the advantages that it owns can be summary as follows:
Fresh agricultural products between the supermarket stores will be allocated optimally to improve the overall profits after adding transverse replenishment. And this can reduce profits loss of the shortage situation when the supermarket stores take no notice of the shortage situation, and when the supermarket stores treat the surplus fresh agricultural products at discount prices, this can reduce profits loss of the surplus situation.
All sub supermarket stores of the supermarket chains are regard as a system. That means that when there is shortage or surplus of fresh agricultural products of some supermarket stores, then the shortage of the part of supermarket stores do not represent the shortage of the supermarket chains system, the surplus stock of the part of supermarket stores can not represent the surplus of the supermarket chains system. From the perspective of system, the transverse replenishment strategy can optimize the fresh agricultural products inventory.
There is not a problem that unstable partnership occurs between the sub supermarket chains stores since all sub supermarket chains stores are unified managed by the headquarters.
The distance between them should be taken into consideration when the sub supermarket stores transfer fresh agricultural products from a store to another store. Therefore, transfer goods between stores can improve arrival rate. For the supermarket stores out of stock, the transport costs of transferring fresh agricultural products from other supermarket stores are much lower than the supply center. And for small quantities of fresh agricultural products out of stock, transfer fresh agricultural products from other sub-goods supermarket stores will be more convenient. This can help short the replenishment time and improve customer service levels to a certain extent.
The replenishment price of fresh agricultural products is relatively stable, which can be controlled between the purchase price of the distribution center and the selling price of the supermarket stores. And it can be priced by headquarters to reduce the replenishment costs.
From what has been described and discussed above, the transverse replenishment has more advantages. It can be used in supermarkets fresh agricultural products replenishment, but it needs to combine the use of traditional replenishment strategy so as to play their strengths. Because it cannot exclude the situation that inventory shortage or excess of the entire supermarket chains will occur. Therefore, the transverse replenishment of fresh agricultural products between stores needs to combine traditional way to provide services of the supermarket chains.
4. Transverse Replenishment Inventory Model and Transportation Model Design
4.1. Problem Descriptions
Due to the certain small demand of fresh agricultural products not up to the required amount of the distribution center, the distribution center is not to carry out the distribution or because the distribution center is relatively far from the supermarket stores, resulting in the shortage situation of fresh agricultural products. When some supermarket stores predict the demand of fresh agricultural products, there is large deviation, which results in excessive accumulation of fresh agricultural products. For the cases above, the transverse replenishment will be applied to supermarket stores, which will be more rational to use the resources fresh agricultural products to further reduce costs and losses.
Transverse replenishment of the supermarket chains fresh agricultural products aims to make the optimal allocation of reasonable inventory of the supermarket fresh agricultural products, to minimize the total costs, and to get the entire optimal system. To solve the issue of the replenishment of the fresh agricultural products between the supermarket chains stores, the transverse replenishment inventory model can be established. Firstly, to make the whole system to the minimum inventory costs, meanwhile, to make optimal replenishment strategies of all stores to the lowest cost. And, finally, the total cost of the entire system will be the lowest.
4.2. Model Assumptions
We assume that the order lead time of fresh agricultural products is same and unchanged. All supermarket stores apply (s, S) storage strategy. The demand of fresh agricultural products is independent and is in keeping with poisson distributions. The operational status of each supermarket store is same. When the stock fresh agricultural products are less than s, then restocking to S. In the case of each supermarket stores appear out of fresh agricultural products, only when the existing inventory below the safety stock quantity, there is replenishment applications from the supermarket stores, which stock stores is greater than the safety stock. The symbols and meanings involved in the model are as follows: Each supermarket chains store is represented as i, j, and N is the total number. The fresh agricultural products inventory of the supermarket chains system is represented as S0, the fresh agricultural products stocks of store i is represented as Si. The ordering cost of fresh agricultural products of each supermarket chains stores is represented as Cr. The unit time fee of fresh agricultural products of each supermarket chains stores is represented as Ch. The Shortage Costs of fresh agricultural products of each supermarket chains stores is represented as Cl. The lateral transportation costs of fresh agricultural products of each supermarket chains stores is represented as Cij, the average transportation cost of the supermarket chains stores is represented as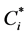 . The probability of supermarket store i meeting the demand of fresh agricultural products with its own stocks is represented as ai. The probability of supermarket store i meeting the demand of fresh agricultural products rely on transverse replenishment is represented as bi. The probability that the fresh agricultural products of supermarket store i out of stock is represented as li. Because only when the fresh agricultural products of entire system is out of stock, then the fresh agricultural products of each supermarket store may is out of stock, therefore, the probability of the shortage of system fresh agricultural products: l = li. The expectation customer service levels of the supermarket chains system is represented as e. The demand of fresh agricultural products of unit time of supermarket stores i is represented as Di; the demand of fresh agricultural products of system is represented as D0; the average demand of each supermarket store is represented as mi; the replenishment quantities from store i to stores j is represented as Dij. The replenishment lead time of fresh agricultural products of each supermarket chains stores is represented as Li. It is the time that from the issue replenishment orders to the commodity storage.
. The probability of supermarket store i meeting the demand of fresh agricultural products with its own stocks is represented as ai. The probability of supermarket store i meeting the demand of fresh agricultural products rely on transverse replenishment is represented as bi. The probability that the fresh agricultural products of supermarket store i out of stock is represented as li. Because only when the fresh agricultural products of entire system is out of stock, then the fresh agricultural products of each supermarket store may is out of stock, therefore, the probability of the shortage of system fresh agricultural products: l = li. The expectation customer service levels of the supermarket chains system is represented as e. The demand of fresh agricultural products of unit time of supermarket stores i is represented as Di; the demand of fresh agricultural products of system is represented as D0; the average demand of each supermarket store is represented as mi; the replenishment quantities from store i to stores j is represented as Dij. The replenishment lead time of fresh agricultural products of each supermarket chains stores is represented as Li. It is the time that from the issue replenishment orders to the commodity storage.
4.3. Model Establishment
The total inventory costs include order costs, storage costs, lateral transportation costs, the shortage loss costs.
For the order costs CR: the order cost of fresh agricultural products can be represented a product by a single order costs and the total number of orders.
 (1)
(1)
In the formula,  represents the actual shortage amount of each time,
represents the actual shortage amount of each time,  represents the total number of orders.
represents the total number of orders.
For the storage costs CH: the order cost of unit time of fresh agricultural products can be represented a product by the unit storage cost and the Average inventory quantities.
Because the model is based on the premise allowing out of stock, so the average inventory quantities do not include the demand quantities in the period of lead time. The average inventory quantities and the storage costs can be got as follows:
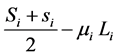
 (2)
(2)
Lateral transportation costs CT: the transverse transportation costs is related with the average transportation costs, the average demand rate of fresh agricultural products and the probability of meeting the demand of fresh agricultural products through transverse transportation.
Throughout the supermarket chains system, there are three cases about the stock demand of fresh agricultural products: 1) the fresh agricultural products of stores can be met through the original stock, then the probability is ai; 2) the fresh agricultural products of stores can be met through lateral transportation, the probability is bi; 3) the entire supermarket system is out of stock, the fresh agricultural products cannot be met, then the probability is li. And, ai + bi + li = 1.
According to independent demand inventory model, in the period of order lead time, the demand of store i is Di Li, then:
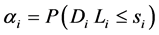 (3)
(3)
If the system is out of stock, it does not meet the conditions of transverse replenishment. Then, the store i is out of stock in the period of optimal ordering, while other stores j is in the lead time or in the period of order cycle. And the demand is always greater than the actual stocks of stores. Then, the probability is as follows:
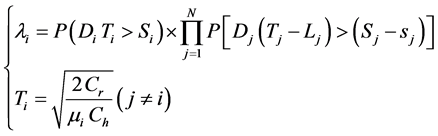 (4)
(4)
Average demand of the supermarket store i mentioned in the parameter setting is mi, but the actual average demand need to be further refined. Some of which are transported from other supermarket stores laterally, and they did not affect the overall system inventory, therefore, they need to be removed. After the transverse replenishment among other stores, there are still unresolved demand, and the demand in this part needs to be calculated in the store i. The actual average demand of the store i fresh agricultural products is derived as follows.
 (5)
(5)
The lateral transportation costs of the whole supermarket chains system can be obtained from the above equation as follows:
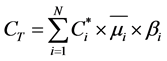 (6)
(6)
The shortage loss costs of the whole supermarket chains system is as follows:
 (7)
(7)
In summary, the inventory total cost model of fresh agricultural products of the supermarket chains system is as follows:
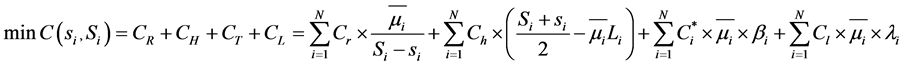 (8)
(8)
s.t. 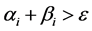
If there is no lateral transportation between supermarket store, the model becomes the follows:
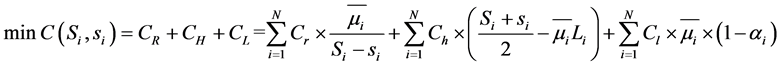 (9)
(9)
s.t. 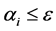
Assume that eventually all fresh agricultural products of the supermarket chains system is distributed to all the sub stores of the supermarket chains system, the model will be the supply and demand balance transport model. m represents the stores that has Surplus, referred to as A1, A2, A3, …, … Am. n represents the stores that has shortage, denoted by B1, B2, B3, …, … Bn. The quantities of surplus is recorded as a1, a2, a3, …, …, … am The quantities of shortage is recorded as b1, b2, b3, …, …, … bn. xij is the transporting capacity of the supermarket chains which is transported from store Ai owning surplus to store Bj that has shortage (i = 1, 2, 3, …, ... m, j = 1, 2, 3, …, … n). Cij represents the unit transportation costs from store Ai to store Bj dij is the distance from store Ai to store Bj, but it will be affected by traffic in the actual transportation process. If it is considered only in distance or unit transportation cost. There will be inaccurate to the distribution program of the whole system. And the traffic situation the day is not the same in each time. rij represents traffic situation coefficients from store Ai to store Bj. rij is only in 0 - 1. The more it is closer to 1, the better the traffic situation it is. On the contrary, it is worse. qij represents the quality factor of fresh agricultural products from store Ai to store Bj. qij is only in 0 - 1. The more it is closer to 1, the better the quality factor it is. On the contrary, if it is closer to 0, it is worse.
When there is shortage of store i, the store i need to make replenishment application to other stores that owning more fresh agricultural products. And, when store i has the surplus of fresh agricultural products goods stores, the surplus that has excess safety stock, needs to be transported to the stores is out of fresh agricultural products. Then, the transverse replenishment transportation model is established on the basis of the traditional transportation model as follows:
![]()
![]() (10)
(10)
5. Application Example One
5.1. Background Description
A supermarket is a national supermarket chains and is the large-scale retail enterprises. There are a total of seven regional chain store, these stores are replenish by the same fresh agricultural products distribution center. In recent years, in order to increase traffic, improve the market competitiveness of industry peers, the supermarket chains increase a significant operating proportion of fresh agricultural products in supermarkets stores, and regard the fresh agricultural products as highlights and features.
Since the distribution center is relatively far from the supermarket stores, or due to the certain small demand of fresh agricultural products not up to the required amount of the distribution center, the distribution center is not to carry out the distribution, resulting in the shortage situation of fresh agricultural products. Because when some supermarket stores predict the demand of fresh agricultural products, there is large deviation, which results in excessive accumulation of fresh agricultural products. And the fresh agricultural products cannot be sold due to the rot, the profit margins of the fresh agricultural products will be reduced. For the cases above, the transverse replenishment will be applied to the supermarket, which will be used to solve the shortage and the surplus problems of fresh agricultural products.
5.2. Data Calculation
The operational status of the seven chain stores is same. The demand of fresh agricultural products is independent and is in keeping with poisson distributions. The order lead time of fresh agricultural products is same and unchanged. All supermarket stores apply (s, S) storage strategy.
Related data are as follows:
1) The Si, si of each supermarket store, the average transportation cost: ![]() is as shown in the Table 1.
is as shown in the Table 1.
2) The single ordering cost: Cr = 1000, the inventory holding costs of a single piece of fresh produce of unit time: Ch = 5, the shortage loss costs of a single piece of fresh agricultural products: Cl = 20.
3) The demand of fresh produce stores varies every day. Criteria to the demand of a month, the average daily demand mi of the store is as shown in Table 1.
The above data are into the formula (1) and formula (2), then the order costs, storage costs can be obtained under the conditions of not allowing transverse replenishment. Figure 1 shows the calculation of order costs by using MATLIB. Figure 2 shows the calculation of storage costs by using MATLIB.
![]()
Table 1. Data of each sub supermarket stores.
![]()
Figure 1. Using matlab to calculate order costs.
![]()
Figure 2. Using matlab to calculate storage costs.
![]()
![]()
4) The demand of fresh agricultural products is in keeping with poisson distributions: Di ~ P (si);
![]() ,
,![]() .
.
The fresh agricultural products of stores can be met through the original stock, and the probability is ai.
According to the Equation (3) and the probability formula of poisson distributions, the ![]() can
can
be got. And the The results are shown in Table 2.
When the supermarket chains system is out of stock, it does not meet the conditions of transverse replenishment. Then, supermarket stores at this time needs to place an order to suppliers or distribution center, the rate of shortage is li, bi. According to Equation (4) and the formula ai + bi + li = 1, the results obtained are shown in Table 3.
5) Derive the probability of the supermarket stores using its own inventory to directly meet demand or the probability of the supermarket stores meet demand through replenishment indirectly. According to the formula 5, the stores actual average demand rate can be got.
![]()
![]()
And so on, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
Table 2. Probability data of store’s own inventory to meet demand.
![]()
Table 3. Probability data of indirect replenishment to meet demand.
6) The above data are into the formula (6) and formula (7), then the lateral transportation costs, the shortage loss costs can be obtained.
![]()
![]()
7) The order costs, storage costs can be obtained under the conditions of allowing transverse replenishment.
![]()
![]()
8) According to the inventory cost model, the total cost of inventory can be obtained under the conditions of allowing transverse replenishment.
![]()
9) When the supermarket chains system does not meet the needs of fresh agricultural products, supermarket stores at this time needs to place an order to suppliers or distribution center. Then, there will be no lateral transportation costs, and the the total cost of inventory is as follows.
![]()
5.3. Results Analysis
With regard to the two inventory costs of allowing the transverse replenishment and not allowing the transverse replenishment, it can be got that the total inventory cost of allowing the transverse replenishment is lower than the total inventory cost of not allowing the transverse replenishment. When the supermarket adopt the transverse replenishment, even though the loss caused by shortages is much lower than ordering directly to the distribution centers, even though it needs bear the cost of transporting in the lateral transportation, and even though the storage costs are slightly higher than the cost of the replenishment adopted by distribution center or supplier, there but is a relatively small impact on the total cost of inventory. Therefore, the supermarket adopt the transverse replenishment can make the total inventory costs of the entire supermarket chains system’s more lower.
6. Application Example Two
6.1. Background Description
Because the transverse replenishment inventory model obtains the total inventory cost of allowing the transverse replenishment is lower than the total inventory cost of not allowing the transverse replenishment. So, it can be provided for the supermarket chains to reduce the loss of fresh agricultural products. After the analysis and calculation of inventory cost model, we can transport the fresh agricultural products from stores owning surplus to store owning shortage. Then, the best transportation plan should be designed in order to transport the fresh agricultural products with the lowest transportation costs.
6.2. Data Calculation
Table 4 shows the unit transportation cost data. Table 5 shows the distance data of stores. Table 6 shows the traffic coefficient merits. Table 7 shows the quality coefficient table of fresh agricultural products. Related data of all stores of a supermarket chains are as follows:
According to the data, the transverse replenishment transportation model can be established.
![]()
Table 4. Stores distance data (unit: kilometers).
![]()
Table 6. Traffic coefficient merits.
![]()
Table 7. Quality coefficient table of fresh agricultural products
![]()
![]()
According to the traditional method of solving the transport model, we first need to calculate the underlying table, which is listed as follows. Table 8 shows the underlying table of table-manipulation method.
For the accuracy of the calculation, Vogel method is used here to find the initial solution. Table 9 shows the initial solution of the transportation program.
Use the potential algorithm to distinguish the optimal initial solution, and the optimal transportation plan is obtained.
A1 Þ B1 (300), A1 Þ B4 (300);
A2 Þ B3 (800);
A3 Þ B2 (500), A3 Þ B3 (200), A3 Þ B4 (500).
6.3. Results Analysis
From the above we can see that he transverse replenishment transport model above get the optimal dispatching scheme between stores, that means when we transport the fresh agricultural products from the surplus supermarket stores to the shortages supermarket stores, this strategy can be used to reduce the transportation costs.
![]()
Table 8. The underlying table of table-manipulation method.
![]()
Table 9. Initial solution of the transportation program.
7. Conclusion
The goal of the research is to minimize the total inventory cost of the overall system in the process of replenishment, to maximize the overall system profits. All the sub-supermarket stores of the supermarket chains are regarded as a whole system to be researched in this paper. This paper applies the transverse replenishment thinking to the replenishment of the supermarket chains, provides the solution to deal with the shortage or surplus of supermarket chains fresh agricultural products, and the shortcomings issue of traditional replenishment methods, and provides the solution to deal with the shortcomings issue of only considering the local interest of the traditional replenishment thinking. By the establishment of the transverse replenishment inventory model and the analysis of the actual examples, it can be concluded that the total inventory cost of allowing the transverse replenishment is lower than the total inventory cost of not allowing the transverse replenishment. Through the establishment of transverse replenishment transportation model, the optimal dispatching scheme between the surplus supermarket and the shortages supermarket is given. This paper can provide a reference for the supermarket chains to deal with the shortage or surplus of fresh agricultural products. And, This will help the supermarket chains to improve sales margins of agricultural products, to reduce the total inventory costs of the whole the supermarket chains system, and to improve the customer service levels.
NOTES
![]()
*Key project of Philosophy and Social Science Research in Beijing (09AbJG299), key project of training plan of Beijing young top-notch ta- lent (CIT&TCD201304109), key projects of Innovation and Entrepreneurship of Beijing Wuzi University (0541605843).