Received 28 March 2016; accepted 31 July 2016; published 3 August 2016

1. Introduction
One of the ways in which prior information can be modeled is by the use of the stochastic restrictions approach. The rationale is based on the fact that it brings efficiency gains in the estimators, naturally, subject to the quality of the information available. In some cases, prior information is derived from economic theory, and imposes restrictions among parameters that should hold in exact terms. This prior information could be included in the model as a deterministic restriction, and the restricted estimator has smaller variance than the non-restricted estimator. In other cases, prior information derives from previous estimations of similar models or samples. This information could be considered an approximation of the unknown parameter, or a range of values that should contain the parameter with some probability. In this case, deterministic restrictions should not be included in the estimation procedure since the restricted estimator will be biased. If this information is not taken into account despite being valuable, the chance of improving the efficiency of the estimator is wasted. An intermediate solution is to include it with uncertainty. This is the idea behind the stochastic restrictions approach and it is shown to bring efficiency gains (as shown in [1] and [2] ) for a linear model under normality of the errors. Nevertheless, stochastic restrictions seem not to have much impact in classic econometrics literature, possibly because of their irrelevance on asymptotic grounds. On the other hand, the Bayesian approach, based on the use of prior information, is increasing its applicability and diffusion in the profession. For instance, related to the mixed logit model (see [3] ), the Bayesian approach brings better results in general than the simulated maximum likelihood estimation, mainly due to the prior information that is not considered in the SML method and possibly due to the high variance of the SML estimator resulting from the high number of simulations needed to implement this method ( [4] and [5] ).
Despite the finite sample efficiency gains of the Theil-Goldberger approach, this result cannot be extended to the asymptotic distributions of the constrained estimator, since the efficiency gain vanishes as sample size increases. This result is proved although not useful for empirical research (see [6] ). The reason is that attending at its purposes, asymptotic theory is a tool which provides approximated finite sample distributions of the estimators. If these estimators are constrained and restrictions are correct, then asymptotic theory does not allow the efficient use of all the available information about parameters. Therefore, it would be interesting to extend the finite sample properties of the estimator under stochastic restrictions to the asymptotic context and then to its approximated distribution. In this paper I show that stochastic restrictions could bring asymptotic efficiency gains under some specific assumptions about the asymptotics of prior information.
The main contribution of this paper is the description of a simulation-based estimator in which prior information is taken into account through the stochastic restrictions approach, also, under the same type of assumptions already introduced in the first objective. Simulation-based methods, as the method of simulated moments [7] [8] , and the I.I. method of [9] (see also [10] [11] , for similar approaches), provide powerful techniques to deal with nonlinear models when traditional methods fail. Nevertheless, there is not a clear way by which prior information can be taken into account in simulation-based estimation methods. In this paper I achieve this goal through the extension of the I.I. method by introducing stochastic restrictions in the initial I.I. criterion, defining the Indirect Inference under Stochastic Restrictions (IIR) estimator and showing efficiency gains when compared to the I.I. estimator.
The structure of the paper is the following: Section 2 provides the motivation for the assumption that supports the main results of this paper, also, I discuss the derived efficiency gains for a traditional estimator in finite sample and asymptotic terms. Section 3 describes the method to combine prior information into the indirect inference criteria through the stochastic restriction approach. Also, asymptotic properties are provided. Section 4 focuses on a macroeconometrics example and numerical evaluation of the efficiency gains of the suggested method, and Section 5 concludes.
2. Stochastic Restrictions
The first result to be shown in this paper is that stochastic restrictions yield asymptotic efficiency gains under specific assumptions. Previously, In this section, I provide the definition of stochastic restriction and describe how it behave in asymptotic terms in a standard framework. I show that in order to obtain efficiency gains derived from the introduction of stochastic restrictions it is needed to assume a particular behavior of the prior information in the asymptotic setup. This particular assumption is also motivated in this section.
Consider a general linear model, 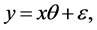 where the parameters of interest is
where the parameters of interest is 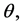 a
a 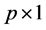 vector. If prior information is available about
vector. If prior information is available about 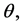 I could model it as follows:
I could model it as follows:
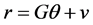 (1)
(1)
which is called a stochastic restriction. In the above equation r is a 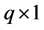 vector (
vector (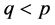 ) containing the values that prior information allocates to a linear combination between parameters, G is the
) containing the values that prior information allocates to a linear combination between parameters, G is the 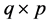 matrix of the para- meters coefficients, and v is a stochastic term that captures the uncertainty about the prior information, for which a distribution is to be assumed.
matrix of the para- meters coefficients, and v is a stochastic term that captures the uncertainty about the prior information, for which a distribution is to be assumed.
Let us show how a stochastic restriction could be defined from prior information in a very simple model formed by a Cobb-Douglas production function 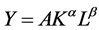 using standard macroeconomics notation. Let us assume that available prior information is that “Returns to scale are probably constant”. This means that we expect
using standard macroeconomics notation. Let us assume that available prior information is that “Returns to scale are probably constant”. This means that we expect 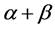 to be close to one. In this case, the stochastic restriction is the equation
to be close to one. In this case, the stochastic restriction is the equation 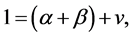 and v is a random term whose variance should capture the uncertainty given to the beliefs about the constancy of the return to scale. In this example
and v is a random term whose variance should capture the uncertainty given to the beliefs about the constancy of the return to scale. In this example 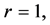
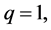 and
and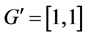 . In general, this restriction need not to be linear, and can be denoted as
. In general, this restriction need not to be linear, and can be denoted as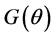 .
.
One of the key element of this paper lies on the particular assumption I make about the asymptotics of![]() . In short, I consider an asymptotically decreasing variance of the stochastic restrictions, or, in terms of [12] , a para- meter sequence. As a result, the relative weights of prior and sample information are preserved in asymptotic terms, which explain efficiency gains as opposed to the standard approach.
. In short, I consider an asymptotically decreasing variance of the stochastic restrictions, or, in terms of [12] , a para- meter sequence. As a result, the relative weights of prior and sample information are preserved in asymptotic terms, which explain efficiency gains as opposed to the standard approach.
This kind of assumption might be considered too strong and, as mentioned in [13] , difficult to justify. However, in the context of IV estimation with weak instruments, in [12] and [14] I use a similar assumption, simply justified by the goal of finding better approximations to the finite sample distribution of the estimator of interest. The approximation is derived mainly from standard asymptotic theory, but also, taking into account the extra assumption of a parameter sequence, designed to improve the properties of the considered estimator. Despite of the objection of [13] , [12] claims, “… since the finite sample distribution does not depend on the behavior of observations in the case of further sampling, there is no reason why an approximation should1. Consequently, there is no need to make such “realistic” assumption … the quality of the approximation is the only criterion for justifiability”. The parameter sequence I choose, as mentioned, is specified on the variance of the stochastic restriction, and using [12] argument, it can also be argued that the rationale lies in the fact that when considered, it makes the asymptotic distribution fit the finite sample distribution better. Yet, in addition, there is a realistic motivation for it: since priors are considered to be obtained from a sample whose size also increases asymptotically, then, it is extended to dynamic terms (defining the asymptotics in terms of both sample sizes) the fact that priors are informative. In other words, our key assumption means that experience matters, which could be considered a natural fact. If priors are informative in static terms, then its quality might increases in the case of additional sampling. Then priors continue to be informative as the size of the sample which generates those increases.
Finally, it is presented an additional argument to motivate the main assumption considered. In a more specific context, the key assumption allows to blend prior and sample information when estimators based on simulation must be used. This is the case of models that generate high nonlinearities in the traditional criterion, making standard methods useless. Generally, the estimators obtained by simulations, despite the fact that are the only solution to estimate some families of models, show high variance, and hence, efficiency gains would be welcomed. The key assumption allows the I.I. procedure becoming a more efficient procedure if stochastic restrictions are correct.
Efficiency Gains
In this section, I discuss the relevance of taking into account prior information in the estimation of a general nonlinear model. First I remind the properties of the nonlinear least squares estimator (![]() ) and of the estimator that takes into account prior information modelled in the form of stochastic restrictions, called the Nonlinear Least Squares under Stochastic Restriction estimator (
) and of the estimator that takes into account prior information modelled in the form of stochastic restrictions, called the Nonlinear Least Squares under Stochastic Restriction estimator (![]() ). Both estimators are compared in terms of their asymptotic variance covariance matrixes
). Both estimators are compared in terms of their asymptotic variance covariance matrixes![]() . Second, I show the irrelevance of the prior information when the standard asymptotic analysis is conducted. Nevertheless, I find the opposite result when a more general analysis is carried out, based on assumptions about the asymptotic behavior of
. Second, I show the irrelevance of the prior information when the standard asymptotic analysis is conducted. Nevertheless, I find the opposite result when a more general analysis is carried out, based on assumptions about the asymptotic behavior of ![]() as mentioned in Section 2.
as mentioned in Section 2.
The purpose of this discussion is to establish formally the setting in which the stochastic restrictions are relevant to explain efficiency gains in the context of a traditional method. This formalization is intended to enhance the understanding of the technical role played by the assumption into![]() , that is, the need for a specific
, that is, the need for a specific ![]() convergence. This allows us in the next section to focus the analysis straight on the construction of the restricted indirect inference estimator once it is known the formal role of the assumption.
convergence. This allows us in the next section to focus the analysis straight on the construction of the restricted indirect inference estimator once it is known the formal role of the assumption.
We start our discussion by considering a general nonlinear model given by the following equation
![]() (2)
(2)
where ![]() is a scalar observable random variable,
is a scalar observable random variable, ![]() is a p-vector of unknown parameters, and
is a p-vector of unknown parameters, and ![]() are i.i.d. unobservable random variables such that
are i.i.d. unobservable random variables such that ![]() and
and ![]() for all t. We assume that
for all t. We assume that ![]() is a vector of
is a vector of
exogenous variables. If ![]() exist and is continuous, the NLS estimator of
exist and is continuous, the NLS estimator of ![]() is defined as the value
is defined as the value ![]() that minimizes the criterion function
that minimizes the criterion function ![]() with respect to
with respect to![]() . Additional assumptions are
. Additional assumptions are
to be considered―see, for instance, [15] ―to prove the consistency and asymptotic normality of the NLS esti-
mator. This assumptions are, in vague terms, the existence and continuity of ![]() and the existence of the limit,
and the existence of the limit,
as T goes to infinity, of the second order derivative of ![]() w.r.t.
w.r.t.![]() . For the sample size T calling
. For the sample size T calling
![]() ?
?![]() matrix ?, the asymptotic distribution of the
matrix ?, the asymptotic distribution of the ![]() estimator is,
estimator is,
![]() . (3)
. (3)
Now I consider a set of q stochastic restrictions on![]() ,
, ![]() modelled through the equation
modelled through the equation ![]() where r is a
where r is a ![]() vector and
vector and ![]() v independent of
v independent of ![]() and
and ![]() 2. Following the Theil-Goldberger approach, the resulting model in which Equation (2) and stochastic restrictions are considered, can be expressed as:
2. Following the Theil-Goldberger approach, the resulting model in which Equation (2) and stochastic restrictions are considered, can be expressed as:
![]() . (4)
. (4)
Since, in general, ![]() , the model shows heteroscedasticity of known structure. Then, the model can be transformed following the Generalized Least Squares (GLS) by premultiplying the system in (4) by matrix P, the square root of
, the model shows heteroscedasticity of known structure. Then, the model can be transformed following the Generalized Least Squares (GLS) by premultiplying the system in (4) by matrix P, the square root of ![]() The resulting model, using a compact notation, becomes:
The resulting model, using a compact notation, becomes:
![]() (5)
(5)
where ![]() is the transformed (
is the transformed (![]() ) dimension vector
) dimension vector![]() ,
, ![]() is the transformed matrix
is the transformed matrix
![]() of (4) and
of (4) and ![]() is the
is the![]() ―vector of homoscedastic disturbances, since
―vector of homoscedastic disturbances, since ![]()
Some additional notation should be introduced. Let ![]() and
and ![]() a
a ![]() matrix. The Nonlinear
matrix. The Nonlinear
Least Squares under Stochastic Restriction (SR) estimator of ![]()
![]() is the NLS estimator of the model (5). In order to simplify the presentation I will omit details of the proofs of the consistency and asymptotic normality of the SR estimator, since these are the same needed for NLS estimator, although in this case, defined on the relevant variables of the transformed model (5) ( see [15] ), for instance. We assume that such required assumptions hold in our model, and hence, asymptotic normality and consistency are obtained. We will call this, Standard Asymptotic Assumptions (SAA), explicitly omitted. After some computation, assuming SAA on model (5), it can be easily proved that the asymptotic distribution of the SR estimator is:
is the NLS estimator of the model (5). In order to simplify the presentation I will omit details of the proofs of the consistency and asymptotic normality of the SR estimator, since these are the same needed for NLS estimator, although in this case, defined on the relevant variables of the transformed model (5) ( see [15] ), for instance. We assume that such required assumptions hold in our model, and hence, asymptotic normality and consistency are obtained. We will call this, Standard Asymptotic Assumptions (SAA), explicitly omitted. After some computation, assuming SAA on model (5), it can be easily proved that the asymptotic distribution of the SR estimator is:
![]() . (6)
. (6)
Our purpose is to compare the asymptotic variance covariance matrix given in (3) and (6), first in the context of the standard asymptotic theory, and also in a general alternative context to be defined, based on the structure of the variance of the error term v. We start first by the standard asymptotic setting where the following result is obtained, already provided by [6] for a linear model.
Proposition 1. Under SAA, the SR and NLS estimators have the same asymptotic variance covariance matrix.
The proof is immediate. Since ![]() is constant,
is constant, ![]() and then,
and then,
![]()
Hence, ![]() as shown in (3)3.
as shown in (3)3.
Proposition 1 shows that stochastic restrictions bring no asymptotic efficiency gains. The irrelevance of the stochastic restrictions is not a satisfactory result for empirical purposes, where the asymptotic distribution has to be used to approximate the variance of the estimator, especially when the sample size is small. The question that arises is whether or not it would be possible to find a theoretical framework to keep the relevance of the stochastic restrictions in asymptotic terms, as stated in [1] for finite samples and normally distributed error term. Also, it is a matter of interest the nature of the conditions under which this theoretical framework would be built up. We give an affirmative answer to the first question, since I obtain in some cases asymptotic efficiency when using stochastic restrictions. Also, I provide an attempt to motivate our assumptions, and to justify such cases.
The new context is based on the idea that prior information about parameters comes from previous experience. Moreover, experience derives from observations that are taken from a sample of size![]() . Since
. Since ![]() increases, prior information consequently improves, that is, is closer to be correct. Observations are generated by a model that is not essentially related with our model of interest, and hence, the disturbance v is independent of
increases, prior information consequently improves, that is, is closer to be correct. Observations are generated by a model that is not essentially related with our model of interest, and hence, the disturbance v is independent of![]() . The asymptotic results in this new framework are to be defined as T and
. The asymptotic results in this new framework are to be defined as T and ![]() goes to infinity. Besides, since I want to describe a general analysis, the ratio
goes to infinity. Besides, since I want to describe a general analysis, the ratio ![]() is allowed to vary from zero to infinity in the limit. The following assumptions are in order to formalize the discussion.
is allowed to vary from zero to infinity in the limit. The following assumptions are in order to formalize the discussion.
Assumption 01 (A01). The variance of v, the error term of the stochastic restriction, is ![]() where
where ![]() is the sample size of the model generating the prior information.
is the sample size of the model generating the prior information.
This assumption states that the quality of the prior information increases asymptotically with![]() . The moti- vation for these assumptions is based on the idea that experience matters as described in Section 24. It should be noted that A01 implies that the term r in the stochastic restriction is also a random term and hence it depends on
. The moti- vation for these assumptions is based on the idea that experience matters as described in Section 24. It should be noted that A01 implies that the term r in the stochastic restriction is also a random term and hence it depends on![]() . In order to capture this feature, it is denoted as
. In order to capture this feature, it is denoted as![]() . Since A01 states that prior information improves with the sample size
. Since A01 states that prior information improves with the sample size![]() , in the limit
, in the limit ![]() should equal
should equal ![]() and be true.
and be true.
The asymptotics is analyzed as T and ![]() goes to infinite, and different growing rates are allowed for T and
goes to infinite, and different growing rates are allowed for T and![]() . The following assumptions formalize the setting where the general analysis is carried out.
. The following assumptions formalize the setting where the general analysis is carried out.
Assumption 02 (A02).![]() .
.
Assumption 03 (A03). ![]()
Assumption 04 (A04). ![]()
The purpose of (A02) is to maintain equal weights of prior information and sample information in the limit. Assumption (A03) states that sample information increases more rapidly than prior information, while (A04) set the opposite. We will show that for the three cases, the variance of the SR vary between an inferior bound, given by the variance of the deterministically restricted estimator (I will simply call this as the restricted estimator and denoted it as![]() ) and a superior bound given by the variance of the non-restricted estimator, i.e.,
) and a superior bound given by the variance of the non-restricted estimator, i.e.,![]() . These results are shown in the following propositions, proved Appendix 1.
. These results are shown in the following propositions, proved Appendix 1.
Proposition 2. Under SAA, (A01) and (A02), ![]()
This result shows that stochastic restrictions brings asymptotic efficiency gains with respect to the NLS esti- mator when sample and prior information increases at the same rate. In other words, Proposition 2 recovers the Theil-Goldberger contribution for asymptotic distributions, and for the resulting approximated finite sample distributions so derived.
Proposition 3. Under SAA, (A01) and (A03),![]() .
.
This result shows that stochastic constraints do not increase efficiency when sample information increases more rapidly than prior information. In other words, Proposition 3 shows the standard asymptotic conclusion of Proposition 1 as a particular case of the general analysis described by assumption A01.
Proposition 4. Under SAA, (A01) and (A04),![]() .
.
This result shows that when prior information increases more rapidly than sample information, stochastic constraints increase efficiency to the level of the restricted estimator![]() . In other words, in the limit, stochastic constraints reach the maximum level of information and efficiency. Then Proposition 4 shows the standard finite sample conclusion obtained in a deterministic constraint setting as a particular case of the general analysis described by assumption A01. The equation of the
. In other words, in the limit, stochastic constraints reach the maximum level of information and efficiency. Then Proposition 4 shows the standard finite sample conclusion obtained in a deterministic constraint setting as a particular case of the general analysis described by assumption A01. The equation of the ![]() is provided, together with the proof, in Appendix 1.
is provided, together with the proof, in Appendix 1.
Finally, in the following proposition I show a concluding result for a varying ![]() from zero to infinity.
from zero to infinity.
Proposition 5. Under (A01), as ![]() increases from zero to infinity,
increases from zero to infinity, ![]() also increase from
also increase from
![]() to
to![]() . That is, if
. That is, if ![]()
![]() then,
then,
1) ![]()
2) ![]()
3) ![]()
We have established a general setting in which several goals are covered. First I have stated a unique analytical context to explain restricted and non-restricted estimators, in the general terms of the stochastic restrictions approach. In this context, restricted and non-restricted estimators are particular cases of![]() , depending on the relative dynamic of sample and prior information. Therefore, when sample information dominates prior infor- mation, the general SR estimator leads to the non-restricted estimator. When prior information dominates sample information, the general SR estimator leads to the restricted estimator. The described discussion in terms of the
, depending on the relative dynamic of sample and prior information. Therefore, when sample information dominates prior infor- mation, the general SR estimator leads to the non-restricted estimator. When prior information dominates sample information, the general SR estimator leads to the restricted estimator. The described discussion in terms of the ![]() ratio could also be interpreted as a way of looking at the variance of the stochastic restriction. For finite sample size, it is easy to see that the same results could be found when
ratio could also be interpreted as a way of looking at the variance of the stochastic restriction. For finite sample size, it is easy to see that the same results could be found when ![]() varies from 0 to infinity5.
varies from 0 to infinity5.
3. Indirect Inference under Stochastic Restrictions
The indirect inference method is a simulation-based moment matching estimation procedure. The general idea is to match the moments of the auxiliary model from the simulated data to observed data to obtain the estimates of the structural parameters. The method of Indirect Inference (I.I.) of [9] and the methods of simulated moments of [11] and [16] (see similar methods in [10] and [17] ), provide a powerful technique to deal with nonlinear models where traditional methods fail. In spite of the wide applicability of these methods, there is not a methodology to take into account prior information in their implementation (see, for example, [18] ). In this section I suggest a way to solve this problem based on the stochastic restriction approach and also on the discussed asymptotic efficiency gain of stochastic restrictions. The analysis will be cast in the framework of the I.I., since this methodology is more general and other simulation-based estimation methods can be viewed as special cases of it. Therefore, notation will follow as closely as possible [9] . The general goal of this section is to provide an example of applicability of the results shown in Section 3, where asymptotic efficiency resulting from stochastic restriction could be theoretically justified. Moreover, this example has empirical implications, since it provides efficiency gains to simulation-based estimators, whose variance is generally high.
First, I define the Indirect Inference under Stochastic Restrictions (IIR) estimation method and provide its distribution. Then, based on the approach introduced in Section 2, I show that the IIR estimator is more efficient than the I.I. method, provided that the stochastic restrictions are asymptotically correct.
In the I.I. approach it is considered a p-dimension vector of parameters ![]() of a model of interest (M), given by a set of T equations of the form
of a model of interest (M), given by a set of T equations of the form ![]() and a j―dimension vector of parameters
and a j―dimension vector of parameters ![]()
![]() of an auxiliary model
of an auxiliary model ![]() given by equations
given by equations ![]() which is easier to handle than the model of interest.
which is easier to handle than the model of interest.
Some facts have to be pointed out in order to understand the principle of the I.I. estimation. It is assumed that it is not feasible to estimate M by mean of a conventional method, due to its complexity or intractability of a conventional criterion for that model. On the other hand, ![]() estimation is feasible by using a traditional method, based on the optimization of a criterion function
estimation is feasible by using a traditional method, based on the optimization of a criterion function ![]() or auxiliary criterion6. As of the optimization on
or auxiliary criterion6. As of the optimization on
![]() it can be obtained the estimate
it can be obtained the estimate ![]() denoted as
denoted as ![]() since the estimate depends indirectly on the implicit parameters
since the estimate depends indirectly on the implicit parameters ![]() driving the data generating process. The binding function
driving the data generating process. The binding function ![]() is defined as the parametric counterpart of the point estimate
is defined as the parametric counterpart of the point estimate ![]() for a given
for a given![]() . The I.I. estimation focuses on the estimation of the function
. The I.I. estimation focuses on the estimation of the function ![]() from
from ![]() for a set of values of
for a set of values of![]() , which generates by simulation independent paths of
, which generates by simulation independent paths of
![]() . The function
. The function ![]() is assumed to be twice differentiable with respect to
is assumed to be twice differentiable with respect to![]() , and
, and ![]() is of
is of
full rank on a neighborhood of![]() . The I.I. estimator of
. The I.I. estimator of![]() , following [9] , is defined as
, following [9] , is defined as
![]()
where ![]() and
and ![]() is a
is a ![]() symmetric and positive definite matrix to be determined
symmetric and positive definite matrix to be determined
below. Under regular assumptions about the auxiliary criterion ![]() and the model―in Appendix 2 this assumptions are shown―the asymptotic distribution of the I.I. estimator is
and the model―in Appendix 2 this assumptions are shown―the asymptotic distribution of the I.I. estimator is
![]()
where
![]()
and ![]() being
being ![]()
![]() being
being ![]() and
and ![]() are matrixes related with properties of the variance-covariance matrix of
are matrixes related with properties of the variance-covariance matrix of ![]() and specified in assumptions (A6) and (A7) in
and specified in assumptions (A6) and (A7) in
Appendix 2.
The matrix ![]() is chosen according to the optimality criterion, and then taken as
is chosen according to the optimality criterion, and then taken as ![]() In this case, the asymptotic variance-covariance matrix of
In this case, the asymptotic variance-covariance matrix of ![]() (taking
(taking![]() ) is
) is
![]() . (7)
. (7)
Since ![]()
![]() could be used in the place of
could be used in the place of ![]() and a consistent estimator of the asymptotic
and a consistent estimator of the asymptotic
variance of ![]() for
for![]() .
.
We now consider the existence of prior information on the parameters of interest ![]() what could formally by written as stochastic restrictions:
what could formally by written as stochastic restrictions: ![]() where
where ![]() and
and ![]() v independent of
v independent of ![]() and u and the parameters of M and
and u and the parameters of M and![]() . Further properties of v are to be specified below. The vector
. Further properties of v are to be specified below. The vector ![]() contains the priors about the parameter constraints, and
contains the priors about the parameter constraints, and ![]() is chosen according to the quality of the prior information.
is chosen according to the quality of the prior information.
Function ![]() that defines constraints between parameters, is differentiable and such that
that defines constraints between parameters, is differentiable and such that ![]() is a
is a
![]() matrix of full rank in a neighborhood of
matrix of full rank in a neighborhood of![]() .
.
It is necessary to introduce some additional notation to define the proposed estimation method. Let
![]()
![]() and
and ![]() a block diagonal matrix, with
a block diagonal matrix, with![]() ,
, ![]() in their diagonal respec-
in their diagonal respec-
tively.
Definition The Indirect Inference under Stochastic Restriction (IIR) estimator of ![]() is
is
![]() (8)
(8)
where
![]()
Some additional assumptions are in order to derive the asymptotic behavior of the IIR estimator.
(A1) - (A7). Are the regular conditions needed to obtain the asymptotic distributions if the I.I. estimator, shown in Appendix 2.
(A8) ![]() is a
is a ![]() matrix of full rank in a neighborhood of
matrix of full rank in a neighborhood of![]() .
.
(A9)![]() .
.
(A10)![]() .
.
Assumption (A9) describes the asymptotic properties of the stochastic restrictions, and it leads to the appro- ximate distribution
![]()
and hence similar to assumption (A01) introduced in Section 3. Again, the rationale behind (A9) is the intention to maintain a constant relative weight between the sample and prior information asymptotically. The relevance of this assumption lies in the fact, already discussed, that under these hypotheses, the approximate distribution for small sample size of the resulting estimator is closer to the observed distribution of the estimator. Note that (A9) implies consistency of the random variable![]() . Again, (A9) will bring efficiency gains in the restricted estimator7. The asymptotic properties of the IIR estimator are derived next.
. Again, (A9) will bring efficiency gains in the restricted estimator7. The asymptotic properties of the IIR estimator are derived next.
Proposition 6 Under assumptions (A1) to (A10), ![]() is consistent, asymptotically normal and has the asymp- totic distribution
is consistent, asymptotically normal and has the asymp- totic distribution
![]()
where
![]()
This result is proved in Appendix 2.
For the optimal matrix ![]() and
and ![]() the variance-covariance matrix reduces to:
the variance-covariance matrix reduces to:
![]() (9)
(9)
where ![]() is the block diagonal matrix with
is the block diagonal matrix with ![]() and
and ![]() in the diagonal.
in the diagonal.
Proposition 7 Under assumptions (A1) to (A10) ![]() is asymptotically more efficient than
is asymptotically more efficient than![]() .
.
To proof this result, I compare Equation (7) and Equation (9). The difference
![]()
is a negative definite matrix, since
![]()
is a positive definite matrix.
4. Empirical Implementation
This section conducts a set of empirical estimations to assess the performance, in terms of bias and efficiency, of the estimation method described in Section 4 compared to the I.I. method.
The model of interest is given by a production function and the perpetual inventory method equation for the capital stock, K, which depends on the depreciation rate, ![]() which is considered to be variable. Hence, the considered model consist basically on the main structure of a growth model. A specific feature of the model is that the capital stock in unknown as it depends on the depreciation rate which is an unknown parameter. The interest of estimating this model is to obtain as a by-product, estimates of the depreciation rate and hence of the physical capital stock of the economy. Three cases are considered for estimating the depreciation rate, as in [19] where
which is considered to be variable. Hence, the considered model consist basically on the main structure of a growth model. A specific feature of the model is that the capital stock in unknown as it depends on the depreciation rate which is an unknown parameter. The interest of estimating this model is to obtain as a by-product, estimates of the depreciation rate and hence of the physical capital stock of the economy. Three cases are considered for estimating the depreciation rate, as in [19] where ![]() is function of certain explanatory variables and a purely random term.
is function of certain explanatory variables and a purely random term.
To go further into the economic motivation of the model, note that K is one of the basic economic aggregates, and following the definition provided by the perpetual inventory method, it is given by:
![]() (10)
(10)
where I is investment and d the depreciation rate, which measures the loss in value of the existing capital stock as it ages. Since d is an unknown parameter, K is not observable and in practice it is usually measured by accounting techniques, which provides not satisfactory figures since, for instance, technological shocks have not effects on the actual value of the net capital stock. One solution to measure the capital stock is by mean of the simultaneous estimation of d jointly with the parameters of a production function, ![]() That is, the estimation of the production function provides, as a by-product, estimates of a variable depreciation rate, which will allow the measurement of the capital stock. If d is not a constant parameter, then the described methodology to estimate it is not trivial, as can be seen in [19] - [22] . Moreover, since d is assumed to be stochastic, its esti- mation poses methodological difficulties which are not solvable by standard methods. In this case, simulation- based estimation methods seems to be adequate to solve the high complexity of the model, considerably increased by the presence of a stochastic parameter. As commonly known, the resulting high variance of the estimator seems to be one of the most important costs of using these methods, but on the other hand, as previously mentioned, possibly compensated by the availability of prior information. The purpose of this section is to suggest the adequacy of the IIR method to estimate the described model, given the feasibility of priors about d. In parti- cular, prior information about the rate of depreciation is available from other sources (e.g. National Accounts, or estimates deriving from similar models), which could help in the estimation of the production function, since convergence of the algorithms is possibly hard to achieve and estimation is costly in efficiency terms. According to this argument, I use the average estimates of d obtained in similar models as the prior information figures to implement the IIR method.
That is, the estimation of the production function provides, as a by-product, estimates of a variable depreciation rate, which will allow the measurement of the capital stock. If d is not a constant parameter, then the described methodology to estimate it is not trivial, as can be seen in [19] - [22] . Moreover, since d is assumed to be stochastic, its esti- mation poses methodological difficulties which are not solvable by standard methods. In this case, simulation- based estimation methods seems to be adequate to solve the high complexity of the model, considerably increased by the presence of a stochastic parameter. As commonly known, the resulting high variance of the estimator seems to be one of the most important costs of using these methods, but on the other hand, as previously mentioned, possibly compensated by the availability of prior information. The purpose of this section is to suggest the adequacy of the IIR method to estimate the described model, given the feasibility of priors about d. In parti- cular, prior information about the rate of depreciation is available from other sources (e.g. National Accounts, or estimates deriving from similar models), which could help in the estimation of the production function, since convergence of the algorithms is possibly hard to achieve and estimation is costly in efficiency terms. According to this argument, I use the average estimates of d obtained in similar models as the prior information figures to implement the IIR method.
The theoretical model of interest is given by a Cobb-Douglas production function, and assuming constant returns to scale becomes:
![]() (11)
(11)
where y, l and k are production, labour and capital stock in logs respectively, ![]() is the elasticity of the capital
is the elasticity of the capital
stock and it is assumed that![]() . The capital stock is given by
. The capital stock is given by
![]() . (12)
. (12)
In the above equation, ![]() is a time dependent parameter and different assumptions are considered about its nature. Three cases are put forward depending on the deterministic part of the depreciation rate: a constant, a dummy variable and the growing rate of
is a time dependent parameter and different assumptions are considered about its nature. Three cases are put forward depending on the deterministic part of the depreciation rate: a constant, a dummy variable and the growing rate of![]() , in order to follow as closely as possible the empirical models considered in [19] where a similar model is estimated, although in that case
, in order to follow as closely as possible the empirical models considered in [19] where a similar model is estimated, although in that case ![]() has no random term. Table 1 shows the main characteristics of the depreciation rate stochastic processes. In case I, the random depreciation rate is a constant plus a disturbance. In cases II and III there is an explanatory variable in the rhs of the equation
has no random term. Table 1 shows the main characteristics of the depreciation rate stochastic processes. In case I, the random depreciation rate is a constant plus a disturbance. In cases II and III there is an explanatory variable in the rhs of the equation
of ![]() following closely the baseline model. The disturbance term is assumed to be
following closely the baseline model. The disturbance term is assumed to be ![]() indepen-
indepen-
dent of ![]() and the whole set of explanatory variables.
and the whole set of explanatory variables.
Besides, the model introduces a prior value ![]() available for the expected sequence
available for the expected sequence![]() . The prior value is taken as the average of the estimated variable depreciation rate in [19] , which is
. The prior value is taken as the average of the estimated variable depreciation rate in [19] , which is ![]() for all of the cases. Finally, in order to make the
for all of the cases. Finally, in order to make the ![]() equation consistent with the stochastic restriction, this is expressed as:
equation consistent with the stochastic restriction, this is expressed as:
![]() (13)
(13)
where ![]() is the sample mean of the explanatory variable of
is the sample mean of the explanatory variable of ![]() (
(![]() or
or ![]() for cases I, II and III
for cases I, II and III
respectively) and v is the error term capturing the uncertainty about![]() . Specifically, the quality of prior infor- mation is determined by the value of
. Specifically, the quality of prior infor- mation is determined by the value of ![]() which is taken to be 0.015, since it leads a plausible approximated interval [0.03, 0.09] for priors on
which is taken to be 0.015, since it leads a plausible approximated interval [0.03, 0.09] for priors on![]() .
.
![]()
Table 1. Patterns for the depreciation rate.
IIR Estimation
The empirical model of interest is formed by the following equations:
![]() (14)
(14)
where data requires ![]() to follow an AR(1) process, modelled as
to follow an AR(1) process, modelled as ![]()
![]() The autorre-
The autorre-
gressive structure ![]() could be understood as a result of total factor productivity shock8. It should be noted that data allows for a structural change for the intercept, captured be
could be understood as a result of total factor productivity shock8. It should be noted that data allows for a structural change for the intercept, captured be![]() . The breaking period is the one which leads to the best fit among all possible dates. As in the baseline estimation (see [19] ),
. The breaking period is the one which leads to the best fit among all possible dates. As in the baseline estimation (see [19] ), ![]() if
if ![]() and
and ![]() elsewhere. For Case II
elsewhere. For Case II ![]() is a dummy variable, which becomes empirically relevant, and given by
is a dummy variable, which becomes empirically relevant, and given by ![]() if
if ![]() and
and ![]() elsewhere. The breaking period is picking selected the best fit among all
elsewhere. The breaking period is picking selected the best fit among all
possible dates. For the Case III equation, the rate explanatory variable ![]() is considered in order to check the
is considered in order to check the
role of the intensiveness in using the capital stock in the depreciation pattern. Finally, it is assumed that
![]()
The parameter vector of model (14) is![]() ―
―![]() only appears in Cases II and III―
only appears in Cases II and III―
which is estimated by IIR using data of the variables y, l, I, ![]()
![]() and z for the sample period 1970-1997. Non-residential investment is considered for the estimation. The data are taken from the Spanish National Statistical Institute and are measured at 1986 prices.
and z for the sample period 1970-1997. Non-residential investment is considered for the estimation. The data are taken from the Spanish National Statistical Institute and are measured at 1986 prices.
The auxiliary criterion is maximum likelihood and the auxiliary model for the IIR estimation is exactly the same model considered in [19] , which is much closed to the model of interest, being in this case the depreciation rate deterministic and no restrictions imposed by the existence of returns to scale into the production function. Henceforth, the equations of the auxiliary empirical model are:
![]() (15)
(15)
where ![]() follows an AR(1) process, given by
follows an AR(1) process, given by ![]()
![]() and
and ![]() Again the
Again the
random error is considered to follow an AR(1), capturing the total factor productivity dynamics and yielding more accurate estimates. Finally, the parameter vector of the auxiliary model (15) is ![]() being
being ![]() only estimated for cases II and III.
only estimated for cases II and III.
The motivation for structure of the auxiliary model relies on the fact that it is a more simple model, since no random term is considered in the equation of the variable rate of depreciation, and, on the other hand, it is a more general model, since no constant returns to scale are imposed in the production function. Very little can be said in priors grounds about the adequacy of one specific model to be the best auxiliary model for I.I. estimating. Nevertheless, it is in general admitted that the model should be similar, and if possible, more general. Both of this characteristics are considered in the selection of the model considered, which is also supported by the empirical results.
As defined in the previous section, the IIR estimator of ![]() is given by:
is given by:
![]()
being![]() , for the specification of the models given in (14) and (15):
, for the specification of the models given in (14) and (15):
![]()
where ![]() and
and ![]() are the ML estimators of the auxiliary model obtained from original and simulated data respectively, S is the number of simulations, taken to be 100,
are the ML estimators of the auxiliary model obtained from original and simulated data respectively, S is the number of simulations, taken to be 100, ![]() is the prior value of
is the prior value of![]() ,
, ![]() the figure capturing the uncertainty about the prior information and
the figure capturing the uncertainty about the prior information and ![]() is the optimal distance matrix, also needed for computing
is the optimal distance matrix, also needed for computing![]() . The term
. The term ![]() is given by the specific equation of the stochastic restriction in each case and
is given by the specific equation of the stochastic restriction in each case and ![]() and
and ![]() are taken to be 0.06 and 0.0015 respectively, as proved in Appendix 2,
are taken to be 0.06 and 0.0015 respectively, as proved in Appendix 2,
![]()
where ![]() and the matrices
and the matrices ![]() and
and ![]() included in
included in ![]() are computed using the numerical derivatives
are computed using the numerical derivatives
involved in the definition, that is ![]() the Hessian of the auxiliary criterion and the outer product of gradient.
the Hessian of the auxiliary criterion and the outer product of gradient.
The ratio ![]() was taken to be equal to one. The reason for this is that since it is numerically equivalent to consider different
was taken to be equal to one. The reason for this is that since it is numerically equivalent to consider different ![]() or
or ![]() to test the sensibility of the results I simply considered alternative values of
to test the sensibility of the results I simply considered alternative values of![]() . Naturally, the estimates of
. Naturally, the estimates of ![]() obtained were closed to
obtained were closed to ![]() as
as ![]() decreases, although
decreases, although ![]() leads to priors for
leads to priors for ![]() weakly supported from previous estimates.
weakly supported from previous estimates.
Table 2 shows the estimates results obtained for all of the cases. Each one of the models has been estimated simultaneously by I.I. and IIR using the same simulation path, in order to test for the efficiency gains and consistency of the results in a more direct way. In all of the cases and for both methods, Table 2 points estimates of the intercept, capital elasticity, coefficient of the AR(1) error term and the variance of the error are fairly closed to those found in the baseline model estimates of [19] , although not always statistically significant.
The point estimate of 0.3 for ![]() is very general admitted for production function estimates. The constant depreciation rate is estimated at 4.5% and 4.0%, for IIR and II respectively, which is higher than the constant and non-stochastic depreciation rate estimate of 3.7% found in the baseline deterministic model. This value is still low when compared to conventional values and more complex specifications seem in order. The remaining results pursue this point. In Case II, columns 4 and 5 give the results obtained allowing for a dummy variable,
is very general admitted for production function estimates. The constant depreciation rate is estimated at 4.5% and 4.0%, for IIR and II respectively, which is higher than the constant and non-stochastic depreciation rate estimate of 3.7% found in the baseline deterministic model. This value is still low when compared to conventional values and more complex specifications seem in order. The remaining results pursue this point. In Case II, columns 4 and 5 give the results obtained allowing for a dummy variable, ![]() which is statistically significant and points to an increased depreciation rate in the second sub sample, yielding an average value for the whole sample close to 6.5%. These are more reasonable results, as discussed above, and again larger vales estimates than in the deterministic
which is statistically significant and points to an increased depreciation rate in the second sub sample, yielding an average value for the whole sample close to 6.5%. These are more reasonable results, as discussed above, and again larger vales estimates than in the deterministic ![]() model.
model.
Columns 6 and 7 give the results for Case III, and the coefficient ![]() is positive for both methods and significant only for IIR method. This would mean that an increase in the GDP growth rate increases the depreci- ation rate, which is consistent result with the fact that an increase in aggregate demand explains an intensive use of capital and then an increase in its depreciation rate.
is positive for both methods and significant only for IIR method. This would mean that an increase in the GDP growth rate increases the depreci- ation rate, which is consistent result with the fact that an increase in aggregate demand explains an intensive use of capital and then an increase in its depreciation rate.
In a more general setting, Table 2 contains several key findings. First, both I.I. and IIR generate estimates
1t-values in brackets.
with very little difference from the baseline model estimates which contains no stochastic depreciation rate. This result allows for confidence in terms of bias and adequacy of the simulation-based methods for the estimation of this specific model, although not significant differences are found for the estimates of the parameters underlying the variable depreciation rate.
Second, IIR is more efficient than I.I., which is shown for the parameter for which prior information is available. In fact, efficiency losses are small provided that I use conservative choices for the variance of the stochastic restriction. Alternative estimations were conducted for different quality levels of the prior information, confirming that efficiency losses are inversely related to the quality of the prior information.
Third, in the implementation of the IIR method, convergence is achieved faster than for the I.I. estimation, which shows that the proposed methodology is a practical way to mix prior and sample information in a simulation-based estimation method. On the other hand, preliminary results suggest that by reducing the number of simulations (say, to 50), it will be possible to reduce the computation time of IIR without adversely affecting its finite sample properties.
5. Conclusions
This paper formalizes some intuitions about the role of prior information on asymptotic rules of inference. In particular, the natural idea that despite prior information is asymptotically irrelevant when modeled through stochastic restrictions, this theoretical result may not avoid using accurate prior information for empirical purposes. Nevertheless, so far there is no any contribution in the literature providing ground for it.
Asymptotic theory is a tool that provides approximate figures for the mean and the variance-covariance matrix of estimators that in general may have an empirical interest, that is, may be one of the few practical solutions to estimate a model of interest. Nevertheless, if prior information is irrelevant in asymptotic terms, it will be so in the derived finite sample approximation of the variance of such estimator. This result of course is not helpful and leads to discard any use of prior information even knowing that prior information in general may be relevant if accurate-in terms of efficiency. This paper is intended to provide an insight in the previous discussion in the sense that if prior information is proved to be asymptotically relevant, then it will also be for the finite sample approximation and thus will bring efficiency gains on empirical ground. This previous discussion is the motivation of this paper and the solution I provide may be understood as a contribution oriented to enhance the usefulness of any estimator as in asymptotic terms there is no room for using prior information in the form of stochastic restrictions.
On the other hand it is worth it to recall the large variance of the I.I. estimator (as well as of others simulation based estimators). This additional setup provides specific motivation to face the challenge of providing theoretical ground for the asymptotic efficiency gains due to stochastic restrictions.
The main contribution, which is the formulation of a new estimator (the IIR estimator), more efficient than the baseline estimator is achieved through the introduction of one specific assumption, which in short is that prior information increases with sample size. This idea, the cornerstone of the suggested approach, is intended to be taken as a potential contribution for the large family of simulation based estimators in the sense that they are now allowed to mix sample and prior information to achieve efficiency gains.
As expected, this discussion is open for future research as empirical results that may be found for testing this insight, may support it or not.
Appendix 1: Asymptotic Variance Covariance Matrix of the SR Estimator
We set the following assumptions to prove Propositions 2 to 5.
(A01).![]() .
.
(A02).![]() .
.
(A03). ![]()
(A04). ![]()
Proposition 2. Under SAA, (A01) and (A02), ![]()
Proof. Under (A01), by construction, the asymptotic distribution of ![]() (6) is now given by
(6) is now given by
![]() . (16)
. (16)
From (A02), ![]() then,
then,
![]()
and
![]()
is a definite negative matrix, and ![]() The resulting approximated distribution for finite sample size is
The resulting approximated distribution for finite sample size is
![]()
what means that efficiency gains are also extended to finite sample distributions.
Proposition 3. Under SAA, (A01) and (A03),![]() .
.
Proof. To prove this proposition I use the general form of the Sherman-Morrison-Woodbury formula (see [23] ), which is
![]() (17)
(17)
where A and C are ![]() matrixes such that
matrixes such that ![]()
![]() exist, and B is a
exist, and B is a ![]() matrix. Now, taking
matrix. Now, taking
![]()
![]() and
and
![]()
From the distribution given in (16) and taking into account Equation (17), I can rewrite ![]() as
as
![]()
since by (A03) ![]() and then,
and then, ![]()
Proposition 4. Under SAA, (A01), and (A04), ![]() where
where ![]() is the restricted nonlinear
is the restricted nonlinear
estimator of the model.
Proof. From the rewritten equation of ![]()
![]() . (18)
. (18)
Since (A04) states that ![]() then,
then,
![]()
and, by substituting the above equation into the equation of ![]() I have
I have
![]()
which is easily checked to be the asymptotic variance covariance matrix of the NLS estimator of the model
![]()
![]()
which is the restricted model.
Proposition 5. Under (A01), and as ![]() increases from zero to infinity,
increases from zero to infinity, ![]() also increases from
also increases from ![]() to
to![]() . That is, if
. That is, if ![]()
![]() then,
then,
1) ![]()
2) ![]()
3) ![]()
Proof. Taking limits in the term where ![]() appears into the Equation (18) I have
appears into the Equation (18) I have
![]() (19)
(19)
and going back to the Equation (18), I have
![]()
Since ![]() then
then ![]() what proves 1).
what proves 1).
From (19),
![]()
![]()
then, by substituting the above results into (18), I obtain ![]() and
and
![]() what proves 2) and 3).
what proves 2) and 3).
Appendix 2: Asymptotic Distribution of IIR Estimator 3 mm
Here I develop similar proofs to the used on the asymptotic properties of the I.I. estimator. To show the asymptotic distribution of IIR estimator I need several regularity conditions, as for the I.I. distribution. The most important are
A1) The general auxiliary criterion function ![]() converges to a deterministic limit denoted by
converges to a deterministic limit denoted by ![]() when T goes to infinity.
when T goes to infinity.
A2) This limit function has a unique maximum with respect to ![]() and this maximum is
and this maximum is![]() . That is,
. That is,
![]()
A3) ![]() and
and ![]() are differentiable with respect to
are differentiable with respect to ![]() and
and![]() .
.
A4) The solution of the asymptotic first order condition ![]() is well defined in
is well defined in ![]() and
and![]() .
.
A5) ![]() and
and ![]() exist.
exist.
A6)![]() .
.
A7) ![]() for
for ![]()
A8) ![]() is of full rank.
is of full rank.
A9)![]() .
.
A10)![]() .
.
Let us first prove the consistency of the IIR estimator. Under assumptions (A1) to (A4), following [9] it is
proved that the intermediate estimators ![]() and
and ![]() (
(![]() to simplify notation) converge to
to simplify notation) converge to ![]()
and ![]() respectively. Also, from (A9),
respectively. Also, from (A9), ![]() Then,
Then,
![]()
Let us now find the asymptotic distribution of![]() . Under assumptions (A1) to (A7), asymptotic expansions
. Under assumptions (A1) to (A7), asymptotic expansions
of ![]() and
and ![]() are deduced from the first order condition. We have, that (following [9] )
are deduced from the first order condition. We have, that (following [9] )
![]() (20)
(20)
and
![]() . (21)
. (21)
The asymptotic expansion of ![]() is deduced as follows. The first order condition for
is deduced as follows. The first order condition for ![]() (
(![]() for short) from the criterion (8) is:
for short) from the criterion (8) is:
![]()
An expansion around the limit value ![]() gives
gives
![]()
since ![]() as shown in the asymptotic properties of the
as shown in the asymptotic properties of the ![]() estimator under the considered assumptions. From (A9) and the consistency of
estimator under the considered assumptions. From (A9) and the consistency of![]() , it follows that
, it follows that ![]() is also
is also![]() . Rewriting the above equation in
. Rewriting the above equation in
the limit, and calling ![]() and
and ![]()
![]() (22)
(22)
From (21), (20), I get
![]()
and using (A6), (A7),
![]()
where ![]() and
and ![]()
Finally, using assumptions (A8), (A9) and (A10):
![]()
where
![]()
The optimal ![]() is
is ![]() by the Gauss-Markov theorem. The AVC matrix of the IIR estimator, taking
by the Gauss-Markov theorem. The AVC matrix of the IIR estimator, taking![]() , is:
, is:
![]()
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
NOTES
![]()
1It is important to note that in Section 3, under standard assumptions, the finite sample efficiency gains due to stochastic restrictions vanishes as the sample size increases. Also in our case the approximated distribution depends on further sampling.
![]()
2Although it is not necessarily, neither realistic that the restrictions should be independent and homoscedastic, assuming that make easier the understanding the effects of stochastic restrictions on efficiency gains.
3The suggested approximated distribution for finite sample SR estimator is ![]()
4As is well known, priors in the Theil-Goldberger approach can also be given the interpretation of the posterior mean of a Bayesian estimator. Following this interpretation, we can also justify A01.
![]()
5This result can be shown on requested to the author.
6This function could be, for instance, the likelihood function, as considered in the example described in Section 5.
7We can also provide in this section a general setting depending of the limit of ![]() as done in Section 3. The arguments and conclusions will be the same. If
as done in Section 3. The arguments and conclusions will be the same. If![]() ,
, ![]() and no efficiency gains are derived. If
and no efficiency gains are derived. If![]() ,
, ![]() reaches its minimum level.
reaches its minimum level.
8Following real business cycle models, a standard assumption for technology consists of a time trend and an innovation which follows an AR(1) process. In this case the error in the production function follows an AR(1), what supports our results.