The First Sharp Diffraction Peak in the Total Structure Function of Amorphous Chalcogenide Glasses: Anomalous Characteristics and Controversial Views ()
Received 31 March 2016; accepted 26 July 2016; published 29 July 2016
1. Introduction
One of the most characteristic features in the diffraction patterns of network-forming glasses and liquids is the so-called first sharp diffraction peak (FSDP) or sometimes called the pre-peak [1] [2] . It appears at a scattering wave vector Q (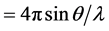
, where 
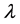is the wavelength of the incident radiation and 
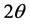is the scattering angle) in the range 1 - 2 Å−1, and it has many structural anomalies [3] that have put this peak a subject of debate for more than two decades ago.
Conventional neutron or X-ray scattering techniques involves measuring the static structure function,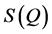 
, of the corresponding material which is then Fourier transformed to obtain the real-space correlations. Here, the 
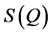function is decomposed into sin waves of constant amplitude. Hence, Fourier transformation of a 
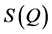that is delocalized over the observed Q-range results in relatively sharp features in the real space, giving rise to the first and second neighbor shells of atoms in the structure, more difficultly, when 
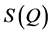has features that are localized in a limited Q-range (such as the FSDP). In this case, Fourier transformation results in rather delocalized features in the real space, conveying little information about the involved interatomic correlations. This difficulty makes it hard to elucidate the precise structural origin of the FSDP, despite the fact that the FSDP gives a clue to the extent of intermediate range order in the amorphous material. The position (Q1) of the FSDP in reciprocal space suggests that Fourier components of period » 
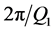» 4 - 6 Å are involved. On the other hand, the correlation length inferred from the width (
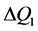) of the FSDP, 
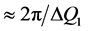, is of the order of 15 - 25 Å, which is a remarkably long range in a solid that by definition has no long-range order.
The FSDP is observed in many different types of non-metallic, non-crystalline materials such as oxy-chalco- genide glasses [4] [5] , AX2 or B2X3 (A = Si, Ge; B = P, As; X = O, S, Se), P4, VCl4 [6] and in zinc halides [7] .
The FSDP is an unmistakable signature of intermediate-range order (IRO) in a glass, and it can potentially offer an insight into the glassy molecular connectivity: whether, e.g., the glassy intermediate-range structure is characterized by the layering of planes of atoms, the bundling of chains of atoms, or a random packing of basic molecular structural units. This range of possibilities suggests the considerable uncertainty in the literature concerning the precise structural origin of the FSDP.
Despite the large number of structural studies of network-forming glasses and liquids, no clear cut has been made about the structural origin of the FSDP. A review of literature about the FSDP shows a wide variety of interpretations about its structural origin, most of them contradict each other despite the relatively general agreement that it is a signature of intermediate range order (IRO) in glasses and liquids.
As the debate on the origin of the FSDP is far from over, here we review and bring together the structural anomalies of the FSDP followed by some interpretations that were proposed for its structural origin. Later, we rule out those interpretations that were proved to be inconsistent with the recent experimental findings, and we finally highlight the most likely interpretations that are-up to date-agreed with the experimental findings.
2. Structural Anomalies of the FSDP
In the following we review structural anomalies of the FSDP as a function of temperature, pressure, and composition for some network-forming glasses and liquids with emphasis on chalcogenide glasses.
The FSDP intensity, position as well as its full width at half maximum (FWHM) do depend on the thermodynamic conditions of the material. They change anomalously with temperature [8] , pressure [9] , and even with composition [10] .
Previous measurements of molten and glassy GeSe2 have been carried out by X-ray [11] - [13] and neutron diffraction [14] - [16] and show a pre-peak around the wave vector Q at about 1.0 Å−1. This indicates the persistence of the FSDP even in the molten state. Price et al. [17] studied the intermediate range order in binary and ternary glasses and they confirmed the persistence of the FSDP even in the liquid phases, especially in liquid GeSe2.
Anomalously, the intensity of the FSDP in the glassy state generally increases with increasing temperature [18] contrary to other peaks in the static structure function,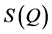 
, which have a decrease in intensity with temperature due to the normal Debye-Waller behavior. Surprisingly, the FSDP also present in the liquid state with almost not much change in intensity [6] [7] [14] [19] [20] . Experimentally, performing a pulsed neutron diffraction experiment on GeSe2, Susman et al. [16] [21] showed that the height of the FSDP in the 1084 K liquid is just 10% less than that in the 10 K glass, with the positions and the half-widths are identical, indicating that GeSe2 retains considerable intermediate-range order in the liquid state.
The FSDP is also remarkably sensitive to variables such as pressure and thermal treatment [3] . When the pressure or density is increased, unlike other peaks in the static structure function,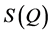 
, the intensity of the FSDP in chalcogenide glasses and in silica [22] - [26] decreases rapidly and shifts in position towards higher values of Q. Its intensity also changes markedly when the glass composition is changed.
Sampath et al. [27] using X-ray and neutron diffraction on GeO2 glass found that the FSDP shifts towards higher Q values, broadens, and becomes less intense when the material is densified. On the other hand, using ab initio molecular-dynamics simulations [28] , effects of hydrostatic compression on the local atomic configuration have been investigated. It was found that there is a relation between the structural change and the density dependence of the FSDP.
The FSDP parameters such as intensity, position, area and FWHM are also strongly varying functions of composition. In our previous publication [29] , we have carried out an atomic pair distribution function (PDF) analysis obtained from high-energy X-ray synchrotron radiation of a series of close-by compositions in the GexSe1-x system with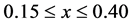
. Remarkably, the FSDP starts as a shoulder in the static structure function, 
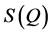, at a scattering wave vector (Q) of about 1.2 Å−1 and shifts towards lower Q values when the Ge content is increased. Other parameters of the FSDP such as area and height increase monotonically with Ge content, having a maximum value at the stoichiometric composition GeSe2 after which they start to decrease with remarkable breaks in slope [29] . The full width at half maximum obtained via different fitting protocols narrows with the increase of Ge content and the FSDP becomes more and more very well defined [29] .
Bychkov et al. [10] also studied the compositional variations of the FSDP parameters for several binary selenide glasses using pulsed-neutron and high-energy X-ray diffraction techniques. Their experimental results showed dramatic changes in the FSDP’s amplitudes (a factor of 10) and positions (»0.5 Å−1).
Moreover, the FSDP intensity decreases markedly upon the addition of network modifier atoms [30] - [32] , as is the case in alkali silicate glasses upon the addition of sodium atoms [33] . Besides, addition of silver to glassy GeSe2 modifies its covalent network as some Ag ions bind with Se atoms, with the effect of breaking up the larger ring structures (i.e. reducing the intermediate range order) and hence reducing the intensity of the FSDP. For other compositions in the GexSe1-x system, the FSDP is rapidly diminished by the addition of silver impurities.
In addition, the FSDP grows up out of a smooth background when tetrahedrally coordinated silicon [34] , phosphorous [9] [35] or germanium [36] is added to amorphous selenium. The presence of rigid tetrahedral units therefore appears to be important in the development of the FSDP.
Furthermore, despite the fact that the position of the FSDP (![]()
) spans a wide range of values for different materials (![]()
Å−1), it has been found [37] [38] that![]()
, where ![]()
is the nearest-neighbour bond length. The FSDP has a full width at half maximum (![]()
) given by![]()
, indicating a correlation length for the intermediate-range order of about![]()
, which is a relatively long distance in a material that has by definition no long-range order.
On the other hand, it has been shown [37] [39] that the FSDP has a similar appearance in glasses which have dimensionalities different from each other, such as![]()
, ![]()
, ![]()
and ![]()
whose crystalline analogs have dimensionality 0, 1, 2, and 3 respectively.
In addition, pronounced FSDPs are also found in liquid semiconductors consisting of equi-atomic binary mixtures of alkali and polyvalent metals [40] .
Moreover, Afifi et al. [41] showed that for g-GeSe2, the correlation length ![]()
associated with the FSDP increases as the annealing temperature increases. In addition, Vashishta et al. [42] using molecular dynamics simulation on glassy SiO2, showed that the FSDP is absent in the charge-charge structure factor, which indicates that charge neutrality prevails over length scales between 4 Å and 8 Å.
In conclusion, upon the forth mentioned anomalous characteristics of the FSDP, it is evident that it is an unusual peak. It behaves anomalously when changing different parameters. This in turn makes it difficult to interpret and to fully address its structural origin, which results in a wide range of different structural interpretations most of them are controversial.
3. Controversial Interpretations of the FSDP
Several interpretations were proposed in literature in order to understand how and why the FSDP manifests. In this section we address most of those interpretations and later we rule out those interpretations that seem to be inconsistent with recent experimental findings.
The formation of clusters in the structure has been proposed to be responsible for the FSDP [3] [43] . In this approach, the FSDP is assumed to be the first and the most intense peak in the inter-cluster structure factor where the origin of the FSDP is attributed to the presence of large molecular clusters with a center-to-center spacing of about 5 Å. If these clusters are quasi planar, a correlation length (R) normal to the planes can be estimated from the pre-peak width [44] as:![]()
, where ![]()
is the full width at half maximum of the pre-peak. This approach was adopted by Afifi et al. [41] where they showed that for g-GeSe2, the correlation length (R) associated with the FSDP increases as the annealing temperature increases, and so, they interpreted this result as an indicator for the formation of small clusters restricted to the nearest-neighbor shell, i.e., the cluster size increases. Consequently, the presence of the pre-peak (FSDP) indicates a strong pointer for the existence of a cluster or medium-range order [41] .
In GeS2 glass, it was proposed [45] that inter-tetrahedral (inter-cluster) correlations based on a particular type of cluster ordering (e.g. parallelization) rather than inter-layer correlations are responsible for the appearance of the FSDP. This interpretation is based on fitting the X-ray scattering curve (including the FSDP) to the experimental one. The best fit obtained is achieved for a parallel ordering of units (clusters) which are parts of ribbons and consist of corner-bound tetrahedra. It was found that these model calculations explain also the anomalous behavior of the FSDP intensity with pressure and with temperature on the basis of changeable inter-cluster distances.
Quasi-crystalline structural configurations have also been proposed to exist in materials having FSDPs [18] [46] - [48] , where via those models the FSDP is assumed to be a single Fourier component in reciprocal space, resulting from the diffraction from a quasi-periodic arrangement of atoms in the real space. The coherence length (d) of such atomic arrangement is determined by![]()
, where ![]()
is the position of the FSDP.
Moreover, the origin of the pre-peak has been attributed to the fact that many materials are crystalline polymorphous having a layer structure with inter-layer separation of the order of 46 Å. Consequently, for some layer-like chalcogenides, it has been proposed that the FSDP is a Bragg-like peak in the static structure function where the diffraction from layers produces the pre-peak [49] .
Uemura et al. [20] using neutron diffraction data suggested that correlations between layers are the origin of the FSDP in a-GeSe2 and that the position and width of the peak are the result of an about 6 Å inter-layer spacing and stacking to about 60 Å in extent (about 10 layers). The magnitude of the oscillations responsible for the FSDP is controlled by the height of the FSDP. Moreover, Armand et al. [50] using differential anomalous X-ray scattering on germanium selenide glasses found that the FSDP, encountered on the total structure factors around 1 Å−1, is due to Ge-Ge correlations in the intermediate range order (6 - 7 Å).
Several crystalline analogs of chalcogenide glasses, such as As2Se3 and GeSe2, exhibit layered structures giving rise to Bragg reflections at reciprocal space position (Q1) of about 1.0 Å−1, and it has been proposed that the glasses are made up of interconnected sections of such layers [49] .
In covalent glasses, the origin of the FSDP has frequently been ascribed to some form of structural element at the intermediate-range length scale (5 - 50 Å) having a direct crystalline counterpart [16] .
Keiji Tanaka [51] constructed ball-and-stick models for the FSDP based on some of its observations and he concluded that the crystalline model originally proposed by Vaipolin and Porai-Koshits provides straightforward explanations for most of its features.
Moreover, Vashishta et al. [52] on their study of chalcogenide glasses interpreted the anomalous temperature dependence of the FSDP, i.e. the decrease in its height on cooling as due to frustration enhanced by the increased density.
In addition, Iyetomi et al. [53] [54] using integral-equation method and interatomic potentials, studied the FSDP in GeSe2 glass and they elucidated its anomalous temperature dependence. They concluded that the rationale behind the FSDP is cooperation of the excluded volume effect and the local charge neutrality leading to the conditional packing of atoms with the formation of Ge(Se1/2)4 tetrahedra. Based on this view, Iyetomi et al. [53] [54] interpreted the anomalous temperature dependence of the FSDP as due to an increase in the number density of the system on cooling.
Taking a different track, a recent study by Christie et al. [55] on amorphous silicon and silica showed that the FSDP can be regarded as arising from scattering from atomic configurations equivalent to a single family of positionally-disordered local Bragg planes having the furthest separation.
More recent works on FSDP in GexSe1-x system reported the observation of structural anomalies in FSDP parameters. In these studies, Wang et al. [56] and Sharma et al. [57] characterized the existence of a stress-free or intermediate phase (IP) within some range of concentration of the chalcogene element.
Many experimental [11] [13] [19] [58] [59] and theoretical [52] [60] [61] results have shown that the FSDP for an AX2 material is determined primarily by cation-centered correlations, and primarily cation-cation ones. Massobrio et al. [62] correlated the appearance of the FSDP in disordered AX2 network-forming materials to the predominant presence of AX4 subunits.
Susman et al. [16] using time-of-flight pulsed neutron diffraction studied different binary chalcogenide glasses of the form AX2 (A = Si or Ge; X = S or Se). Namely, they studied SiS2, SiSe2, GeS2, and GeSe2 and they reported that the origin of the FSDP in these systems is due to correlations within extended ring structures, and that the FSDP arises predominantly from A-A and A-X correlations in the rings.
Moreover, in their study of the compositional variations of the FSDP parameters for several binary selenide glasses, Bychkov et al. [10] have found an empirical relationship between the compositional dependence of the FSDP position and the local coordination number of the guest atom. They also found that the compositional evolution of the intermediate-range order is closely related to variations in the local order. Consequently, the FSDP reflects multiple changes in the glass network on both the short- and intermediate-range scales. On the short-range order, formation of cation-cation homopolar bonds plays an essential role in the development of the FSDP parameters (amplitude, position and FWHM). Moreover, on the intermediate-range order, the FSDP parameters reflect structural insights about the linkages of the basic structural units in the material (for example, random versus nonrandom distribution of the basic structural units).
Molecular dynamics (MD) [52] [63] studies suggest that the origin of the FSDP in GeSe2 glass is principally due to the Ge-Ge correlations in the structure. This result is qualitatively supported by the partial atomic pair distribution function studies (partial-PDFs) measured by Penfold and Salmon [64] where the FSDP was only significant in the Ge-Ge partial structure factor, ![]()
, though other predictions of the MD studies were less well borne out by the measured partials [64] .
Very recently, we have modeled the local structure of Ge0.20Se0.80 glass using reverse monte carlo (RMC) modeling [65] . This glass forms the rigidity percolation threshold in the GexSe1-x glassy networks. Our RMC results indicate that the FSDP arises predominantly from Ge-Ge correlations where it shows up mainly in the Ge-Ge partial static structure function, ![]()
, but not in the ![]()
or![]()
. Our RMC simulation results agree well with those obtained via molecular dynamics [52] [63] .
Moreover, for covalent glasses, models such as random packing of structural units have been proposed to elucidate the structural origin of the FSDP and to quantitatively calculate its different parameters [3] .
Uchino et al. [66] applied “real-reciprocal space analysis” using the continuous wavelet transform technique, to the experimental neutron and X-ray structure factors of silica glass. Their goal was to elucidate a correlation between the FSDP and the corresponding length scale in real space. They reported that the dominant interatomic distance linked to the FSDP in silica glass is about 5 Å, though other longer distances are important and makes an exponentially decreasing contribution.
Very recently, Crupi et al. [67] studied the structural origin of the FSDP in alkaline borate glasses using neutron diffraction technique, from which they proposed that the FSDP in these glasses arises from the periodicity of the boundaries of voids in the random network and explained its compositional and pressure dependencies. In this framework, the planar section of a void is an n-membered ring of all-side vertex sharing basic structural units.
On the other hand, a recent study of a series of alkaline borate glasses at different metal oxide content using neutron diffraction has found strong differences in the intermediate range order as a function of the specific alkaline ion and of its concentration. In that study, Crupi et al. [68] concluded that the FSDP arises from correlations of atoms of voids and showed that the compositional variation of this peak intensity in alkaline borate glasses is due to changes in the distribution of void sizes within the three-dimensional network.
In conclusion, S. R. Elliott in his pioneer works [69] [70] proposed a model for the occurrence of the FSDP in glasses. In this model, the FSDP results from the presence of zones of low atomic occupancy (interstitial voids in the structure). Based on this model, the FSDP is a chemical-order pre-peak due to interstitial volume around cation-centered structural units. Through this model, the calculated FSDP positions of some covalent glasses agree well with experiment, and the anomalous temperature and pressure dependencies of the FSDP can be understood in terms of density effects.
In this view, S. R. Elliott showed that the FSDP is a pre-peak in the concentration-concentration structure factor due to the mentioned chemical ordering of interstitial voids around cation-centered clusters in the structure.
This model of interpretation not only can predict quantitatively the positions of the FSDP for a wide range of oxide and chalcogenide glasses and liquids but also can successfully rationalize the anomalous temperature and pressure behavior of the FSDP intensity and can explain the effect of incorporation of network modifiers on the FSDP.
4. Discussion
In this section we discuss the validity of the forth mentioned proposals about the structural origin of the FSDP, checking their correctness and expectations against recent experimental data. The most likely structural models about the origin of the FSDP are highlighted.
A successful model that treats the microscopic origin of the FSDP should be capable of being generalized to all the glasses of a given class, and should be capable of being used to quantitatively calculate the peak position, half width and intensity and finally should be able to explain the temperature and pressure anomalies of the FSDP. In the following we apply this criterion in ruling out or highlighting a proposed model for the structural origin of the FSDP.
For the quasi-crystalline model, as many experimental findings [6] [7] [14] [16] [19] [20] have shown that the FSDP persists even in the liquid state with undiminished intensity, it is unlikely that quasi-crystalline layers of correlation length of about 20 - 30 Å will persist in the molten and liquid states. This result ruled out the quasi-crystalline model and makes it very unlikely.
In addition, occurrence of the FSDP in materials that do not have layer-like structures such as SiO2 makes the quasi-crystalline model a non generic interpretation. Besides, a sharp diffraction peak at a low wave vector ![]()
can be produced by the random packing of structural units which have dimensions on the order of![]()
, and hence, a layered or two-dimensional structure is not required [3] .
On the other hand, despite the fact that many authors have stressed on the cluster model [3] - [5] [43] , S. R. Elliott [69] has shown that the FSDP in this model has a minimal structural significance and he showed that the structural identity of such clusters in the structure of glasses remains obscure.
S. R. Elliott [71] ascribed the FSDP to a chemical-order pre-peak in the concentration-concentration partial structure factor, ![]()
, associated with the ordering of interstitial voids around cation-centered clusters in the structure. Through this model, not only the deposition of the FSDP of AX2-type glasses can be predicted quantitatively, but also, the anomalous behavior of the FSDP as a function of temperature, pressure and modifier-ion content can all be understood via this elegant interpretation.
A recent study [68] stressed that interstitial (empty and/or filled) voids, having different sizes, can provide a general explanation for all anomalous behaviors revealed for the FSDP.
The interstitial void interpretation of S. R. Elliott [69] about the structural origin of the FSDP seems to be the most successful interpretation. In this model, the chemical ordering of the interstitial voids (zones of low atomic occupancy) in the structure is responsible for giving rise to the FSDP. This model can quantitatively predict the positions of the FSDP for a wide range of oxide and chalcogenide glasses and liquids and can also successfully justify the anomalous behavior of FSDP intensity at different temperature and pressure values and finally can explain the effect of addition of network modifiers.
In this model, the FSDP is a pre-peak in the concentration-concentration partial structure factor ![]()
in the Bhatia-Thornton formalism [72] . It arises due to the chemical short-range ordering of interstitial voids around cation-centered regions in the structure of glass or liquid [69] . This picture assumes that the structure is composed of aggregate of cation-centered quasi-spherical regions, separated by the average cation-cation distance. Each such region is surrounded by quasi-spherical voids, which in turn forms a density fluctuation among the whole structure. This void-based interpretation of the FSDP is not restricted to a particular type of materials, on the contrary, it has a complete generality.
5. Conclusions
The FSDP is observed in many different types of non-metallic, non-crystalline materials such as oxy-chalcoge- nide glasses AX2 or B2X3 (A = Si, Ge; B = P, As; X = O, S, Se), P4, VCl4 and in zinc halides. It is a signature of intermediate-range order (IRO) in a glass, and it can potentially offer an insight into the glassy molecular connectivity.
The FSDP appears at a scattering wave vector ![]()
in the range 1 - 2 Å−1 in the total scattering structure function. The position of the FSDP in reciprocal space suggests that Fourier components of period » ![]()
» 4 - 6 Å are involved. On the other hand, the correlation length (R) inferred from the width of the FSDP (![]()
) is of the order of 15 - 25 Å, which is relatively long in an amorphous material.
The FSDP has many structural anomalies that have put this peak a subject of debate for more than two decades ago. Its intensity, position as well as its full width at half maximum (FWHM) are all depend on the thermodynamic conditions of the material. They change anomalously with temperature, pressure, and even with composition.
Several hypotheses were proposed in literature in order to understand how and why the FSDP manifests. The formation of clusters in the structure has been proposed to be responsible for the FSDP. In addition, quasi-cry- stalline structural configurations have also been proposed to exist in materials having FSDPs. Moreover, it has been proposed that the FSDP is a Bragg-like peak in the static structure function where the diffraction from layers produces the pre-peak.
Many experimental and theoretical results have shown that the FSDP for an AX2 material is determined primarily by cation-centered correlations, and primarily cation-cation ones. In addition, it has been reported that the origin of the FSDP in different binary chalcogenide glasses of the form AX2 (A = Si or Ge; X = S or Se) is due to correlations within extended ring structures, and that the FSDP arises predominantly from A-A and A-X correlations in the rings. Besides, a model has been proposed for the occurrence of the FSDP where it assumes that the FSDP in alkaline borate glasses arises from the periodicity of the boundaries of voids in the random network.
Finally, a model for the occurrence of the FSDP in glasses has been proposed by S. R. Elliott in which the FSDP results from the presence of zones of low atomic occupancy (interstitial voids in the structure). Based on this model, the FSDP is a chemical-order pre-peak due to interstitial volume around cation-centered structural units.
In conclusion, it seems that the most successful model-up to date-is the Elliott’s void model, as it is not only can predict quantitatively the positions of the FSDP for a wide range of oxide and chalcogenide glasses and liquids but also can successfully rationalize the anomalous temperature and pressure behavior of the FSDP intensity and can explain the effect of incorporation of network modifiers on the FSDP.
Acknowledgements
Fruitful discussions with Professor Simon Billinge at Columbia University and Professor David Drabold at Ohio University are highly appreciated.