Polarizabilities and Orientational Order Parameter in N-(p-n-Ethoxybenzylidene)- p-n-Alkoxy Anilines, 2O.Om LC Compounds ()
Received 29 June 2016; accepted 25 July 2016; published 28 July 2016

1. Introduction
Optical and dielectric anisotropic studies on liquid crystals will provide information regarding their viability to be used in applications or not. Optical studies and the birefringence have been obtained in a number of liquid crystals [1] - [7] recently and obtained the order parameter both directly from birefringence following the procedure adopted by Kuczynski et al. and from polarizabilities by using different techniques. The advantage in first method is that the orientational order parameter, S can be calculated in smectic phase also provided that the refractive indices are also obtained in the smectic phases. This is not possible in the later case as particular type of internal field has to be chosen in the nematic phase along with density values. At present there are two models available due to Vuks [8] and Neugebauer [9] . Vuks proposed an isotropic model while Neugebauer considered the nematic phase as anisotropic. Both the models will provide the polarizabilities αe and αo and thereby dα the polarizability anisotropy experimentally. In the perfect order (in the crystalline state) the anisotropy can be obtained semi empirically by following Lippincott and vibrtional methods. Then the order parameter, S is given by dα/Dα.
The systematic studies on these compounds show that the order parameter, S obtained from the Vukas model is more favorable to explain the nematic phase with few exceptions [10] .
This paper presents the refractive index results with temperature and the evaluation of dα and Dα in number of LC compounds of the homologous series, N-(p-n-ethoxybenzylidene)-p-n-alkoxy anilines, 2O.Om where m = 3, 4 and 6 to 10. The one with m = 5 is already published [11] .
2. Experimental
The present compounds are synthesized following the established procedure reported in the literature [11] . The respective p-n ethyloxy benzaldehyde and the corresponding alkoxy anilines are taken in equi-molar proportions in absolute ethanol and refluxed for four hours in the presence of few drops of glacial acetic acid. The glacial aetic acid acts as catalyst. After refluxing the reactions for four hours, the solvent was removed by distillation under reduced pressure. The crude sample was subjected to repeated recrystallization from absolute ethanol in cold to give the pure compound, until the transition temperatures are constant.
The molecular formula of the compounds is given below.
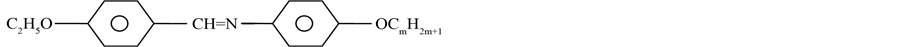
where m = 3 to 4 and 6 to 10.
The refractive indices of all LC compounds are measured using a modified spectrometer. The temperature accuracy is ±0.1˚C. The refractive indices ne and no are measured at wavelength 589 nm. These are measured with a wedge-shaped glass cell, similar to the one used to obtain birefringence by Haller et al. [12] A wedge- shaped glass cell was formed with two optically flat rectangular glass plates (50 mm × 25 mm) sandwiched with glass plate (0.4 mm) which acts as a wedge spacer. The optical flats are uniformly rubbed along the short edge to get the alignment of the LC molecule. The cell is filled with the LC material in the isotropic phases. The nematic LC in the cell acts as a uniaxial crystal with its optic axis parallel to the edge of the spacer glass plate. The temperature accuracy of the heating block was ±0.1˚C. The accuracy in the measured refractive indices was ±0.0005. The refractive index in the isotropic phase (niso) shows a very nominal increment with decrease of temperature. At the isotropic-nematic (IN) phase transformation, the isotropic ray splits into two rays which indicates the onset of birefringence, one value higher and another lower than the isotropic value corresponding to extraordinary (ne) and ordinary refractive (no) indices, respectively. This is clearly observed in the telescope of the modified spectrometer at the angle of minimum deviation. In the nematic region, ne increases and no decreases with decrease of temperature. The transition temperatures along with the enthalpy values are given in reference [13] .
3. Results and Discussion
3.1. Optical Birefringence Studies (Refractive Indices ne and no) in 2O.Om Compounds
The refractive indices of 2O.Om liquid crystals are measured using the modified spectrometer (the details are described in the experimental section) and a wedge shaped cell. The temperature accuracy is ±0.1˚C. This is clearly shown in Figure 1 and Figure 2 for the case of 2O.O9 and 2O.O10 respectively.
![]()
Figure 1. Variation of ne and no with temperature in 2O.O9.
![]()
Figure 2. Variation of ne and no with temperature in 2O.O10.
The refractive indices variations with temperature in the isotropic and nematic phases are illustrated in Figure 1 and Figure 2 for the compounds 2O.O9 and 2O.O10 as representative cases respectively. The IN transition temperatures observed in the birefringence measurements are in agreement with those observed in density measurements. In the case of all compounds dn = (ne − no) with reduced temperature is shown in Figure 3. Further, it is observed in the case of 2O.O10 the refractive indices could not be measured in smectic-C phase as the splitting has a hazy appearance and the splitting could not be detected.
3.2. Estimation of Order Parameter
The orientational order parameter S is evaluated using different methods for all the compounds viz.
1) S calculated using polarizability anisotropy calculated by Lippincott d-function method and the molecular polarizabilities obtained from Vuks model.
2) S calculated using polarizability anisotropy calculated by Lippincott d-function method and the molecular polarizabilities obtained from Neugebauer model.
3) S calculated using polarizability anisotropy calculated using molecular vibration method and the molecular
![]()
Figure 3. Variation of dn with the reduced temperature in 2O.Om materials.
polarizabilities obtained using Vuks model.
4) S calculated using polarizability anisotropy calculated using molecular vibration method and the molecular polarizabilities obtained using Neugebauer model.
5) S calculated using Vuks scaling factor, and
6) S calculated using Neugebauer f(B) parameter.
These values are compared with that S value calculated from dn, birefringence.
3.3. Estimation of Order Parameter “S” from Polarizabilities
For the estimation of the order parameter S from the molecular polarizabilities ae and ao the following equation is used
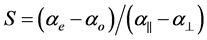 (1)
(1)
where a|| and a^ are the principal polarizabilities and they can be estimated using different methods including the semi empirical methods due to Lippincott and molecular vibration techniques [14] [15] . The two methods are well described. For the sake of compactness the whole procedures are not described here. Further, the molecular anisotropy can be obtained from the Haller extrapolation technique using the experimentally evaluated molecular polarizabilities from refractive index and density data. The molecular polarizabilities ae and ao are evaluated assuming a local field that the nematic molecule experiences. Vuks [8] and Neugebauer [9] proposed two different types of local fields. According to Vuks the nematic molecule experiences an isotropic field while Neugebauer proposed an anisotropic field to the nematic molecule. The methods used, the expressions employed and the procedures adopted are described below in each case for a ready reference.
3.4. Estimation of Molecular Polarizabilities from Refractive Indices and Density
The extraordinary (ae) and ordinary (ao) polarizabilities corresponding to the electric vector parallel and perpendicular to the optic axis are given as
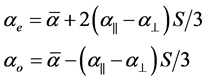 (2)
(2)
where S is the order parameter a|| and 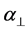 are polarizabilities of the molecule parallel and perpendicular to the long molecular axis of the liquid crystal molecule. The average molecular polarizability
are polarizabilities of the molecule parallel and perpendicular to the long molecular axis of the liquid crystal molecule. The average molecular polarizability  is given as
is given as
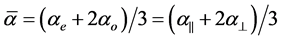 (3)
(3)
Combining the above two equations S, the order parameter is
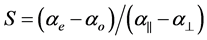 (4)
(4)
For the estimation of the molecular polarizabilities of liquid crystal molecules, the authors have considered both the models, one due to Vuks which considers the local field of the molecule as isotropic and the other due to Neugebauer which considers the local field as anisotropic. The relevant equations of the two models for the calculation of molecular polarizabilities are given below.
3.4.1. Vuks Method
This model was first applied to liquid crystal molecules by Chandrasekhar et al. [16] assuming the internal field as isotropic even in anisotropic crystal. These assumptions lead to the following equations.
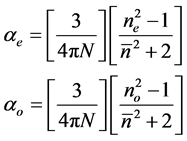 (5)
(5)
where N is the number of molecules per unit volume, ne and no are the extraordinary and ordinary refractive indices of the liquid crystal molecule.

and N = NAr/M where NA is the Avogadro number, r is the density and M is the molecular weight.
3.4.2. Neugebauer Method
Subramanyam et al. [17] applied this method to liquid crystal molecule. According to this method the molecular polarizabilities are
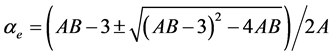 (6)
(6)
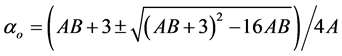 (7)
(7)
where
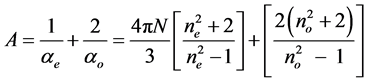 (8)
(8)
![]() (9)
(9)
Ni is the number of molecules per unit volume in the isotropic phase.
Using the two models the molecular polarizabilities, ae and ao of all the liquid crystals are evaluated from the birefringence, dn = (ne − no) and density.
The two methods (Lippincott and vibrational) are used to estimate the polarizability components as well as mean polarizabilities for the 2O.Om compounds and the values are given in Table 1.
3.5. Estimation of Order Parameter, S from Haller’s Extrapolation, Scaling Factor (Vuks) and f(B) Parameter (Neugebauer)
The corresponding expressions are given below.
![]()
Table 1. Parallel, perpendicular components and mean polarizabilities of 7O.Om compounds (10−24 cm3).
3.5.1. Vuks Method
The order parameter is given by [18] [19]
![]() (10)
(10)
where
![]()
3.5.2. Neugebauer Method
In the Neugebauer method [18] [20] the order parameter S is given
![]() (11)
(11)
where
![]()
and
![]()
The scaling factors for the determination of order parameter are obtained in both the cases by plotting log-log
plots between ![]() and f(B) in Vuks and Neugebauer cases respectively against
and f(B) in Vuks and Neugebauer cases respectively against ![]()
i.e., the reduced temperature.
These two methods (Lippicott d-function and vibrational) are used to evaluate the polarizability anisotropy components as well as mean polarizabilities for the 2O.Om compounds and the values are given in Table 2 and Table 3.
The order parameter, S from the molecular polarizabilities is estimated by assuming Vuks and Neugebauer internal field models. Figures 4-10 represent the variation of order parameter, S with the reduced temperature for all the compounds using the two field models ((a) Vuks and (b) Neugbauer) and the values are compared with the value that is obtained either from dn or αg which are identically equal to one another.
![]()
Table 2. Values of ΣbL, ΣbT and (ΣbL − ΣbT).
n value (1.09) included in parallel component of polarizability.
![]()
Table 3. Percentage of deviations of order parameter, S estimated assuming the two field models, using different methods from that obtained using dn, the birefringence in 2O.Om compounds.
4. Conclusions
The refractive index and density are measured with the temperature in all the compounds of 2O.Om homologues. It is found from density measurements the isotropic nematic transition is of first order as expected and the nematic SmC phase in 2O.O10 compound also exhibited first order. A table has been prepared which provides the percentage of deviation of S value from all the methods to that calculated from Dn, the birefringence in perfect order. (The error in the value of S from Dn is about 10%). If the deviation is ≤10%, the values are underlined so that they can be considered in agreement with S from Dn.
The salient features observed from the results are:
1) From Figures 4-10 no preference can be given to any field model unlike the case of other liquid crystal compounds [7] . The positive values in Table 3 depict the higher value of S obtained from dn, the birefringence.
2) Except in the case of compounds 2O.O3 and 2O.O10 the value calculated from f(B) is very much smaller and is the similar case with other LC compounds [7] .
3) Surprisingly, the compound 2O.O9 is not accepting the two models and the S values calculated using the two models are very much smaller when compared to S from dn.
4) In the case of compounds 2O.O4, 2O.O6 and 2O.O7 except the cases of f(B) parameter, the deviations of S value are small.
5) One thing can be stated that the f(B) parameter needs some fine tuning, to have S values similar to that obtained from the field models and from dn and αg.
![]()
Figure 4. (a) (b) Variation of order parameter with the reduced temperature in 2O.O3.
![]()
Figure 5. (a) (b) Variation of order parameter with the reduced temperature in 2O.O4.
![]()
Figure 6. (a) (b) Variation of order parameter with the reduced temperature in 2O.O6.
![]()
Figure 7. (a) (b) Variation of order parameter with the reduced temperature in 2O.O7.
![]()
Figure 8. (a) (b) Variation of order parameter with the reduced temperature in 2O.O8.
![]()
Figure 9. (a) (b) Variation of order parameter with the reduced temperature in 2O.O9.
![]()
Figure 10. (a) (b) Variation of order parameter with the reduced temperature in 2O.O10.
Acknowledgements
Mr. P. S. Sastry and DR. Ch. Srinivasu thank the Principal and the management of Andhra Lyola College, Vijayawada for their help. The authors Dr. P. Pardha Saradhi and Dr. V. G. K. M. Pisipati express their thank to The Head, ECE Department and the Management of K. L. University, Vaddeswaram 522 502, India for providing facilities.
NOTES
![]()
*Corresponding author.